基于LINGO的债券组合投资方案优化

杨 友，谢宇鹏，李 晗，刘亚利

(1.河北北方学院 经济管理学院，河北 张家口 075000;2.河北北方学院 农林科技学院,河北 张家口 075000;3.河北北方学院 理学院,河北 张家口 075000)

债券是发行者以筹集资金为目的，约定自购买方购买后，在某一时间支付购买方某一比例的利息，并在到期时偿还本金的一种有价证券。债券作为一种债权债务凭证，与其他有价证券一样，也是一种虚拟资本，具有偿还性、流动性、安全性和收益性等特征。据中国经济监测中心调查表明，随着国内经济的发展，居民的投资意识逐渐增强，而且随着股市的调整，债券的投资价值重新得到市场的公认。对于投资者而言，依据债券的自身特性和投资环境，如何选择合适的方案来进行债券组合投资就显得十分重要。

众多投资者和研究人员对债券组合投资方案设计的关注点伴随时间的推移也在不断发生变化。在20世纪60年代至70年代初，投资者由通过偿还期策略被动投资转变成为债券投资组合；70年代到80年代初，由于投资环境的改变，债券市场的收益产生剧烈波动；此后，中国逐渐出现了更多的免疫策略来满足机构投资者的新需求[1]。2020年初，随着新冠肺炎疫情的暴发，生产、消费需求骤减，实体经济受到严重冲击，许多企业面临经营困难。为应对疫情、支持企业复工复产，国家及政府部门纷纷出台扶持政策，因此资本市场也加大了对疫情防控领域的支持力度，疫情防控债券应运而生，成为这个特殊时期市场关注的热点[2]。众多学者采用多种理论和方法对投资组合做出不同的分析，L.Duan[3]把动态规划理论应用在多期均值方差模型上，得到投资组合有效边界的解析式，并为投资组合提供了理论参考。丁秀英等[4]采用波动调整法分别对CM、CPPI和TIPP策略绩效进行探究，证明在市场不同价格期，采用最优配置可以为求解投资者的个人跨期动态投资组合保险决策问题提供依据。R.C.Merton[5]在研究资产组合收益时认为托宾分离定律考查的是单期的情形，而Canner得出随着投资风险规避系数升高，债券与股票投资的比例也随之升高。姚远等[6]在Merton得出最优投资组合和消费模型的基础上，对动态投资组合保险建模进行了扩展，从而得到保险者最优的投资策略，以及明确了投资模型策略与市场风险的相关性；金晶晶[7]利用Lingo对某数学规划模型进行求解，探讨LINGO在求解较大规模数学规划模型中发挥的作用。另外，为探讨资产收益可预测性对投资者如何选择最优资产组合的影响，杨朝军、陈浩武等[8]以国内证券市场历史数据为依据，从而进一步证实在长期投资期限下，股票市场收益具有一定的可预测性，为不同投资者提供资产配置建议。陈志明等[9]将债券的信用风险作为投资收益的内生变量，得出违约率对债券投资的影响要大于收益率的影响，债券组合投资方案的制定应着重考虑风险因素。王伟等[10]研究了58个母国的头寸数据，对双边债券类FPI进行实证研究，发现国家风险对于双边债券类FPI的影响会随着金融风险的转移而发生变化，其影响是多角度的、不对称的。信怀义[11]对2003年至2016年的政府证券统计数据进行分析，结合债券组合收益曲线研究债券组合利率风险对投资策略的影响，对商业银行的债券投资操作提出优化策略。

综上所述，以上研究者在债券组合投资方案设计方面做出了较为深入的研究，但是将线性规划数学建模应用于债券组合投资方案研究的较少，所以本研究以2020年河北省研究生建模竞赛题目B题为案例，探究Lingo在债券组合投资方面的应用，分析债券投资的风险与收益，以实现债券组合投资的利益最大化为目标，建立债券高收益规划模型，探索更加科学合理的债券组合投资方案。

1 理论基础

1.1 债券投资组合

债券投资组合是投资人或者金融机构基于安全性和收益性的双重考虑，利用所持有资金对债券及其衍生产品进行多层面、多领域的组合，将安全性较高的无风险资产和收益性较高的风险资产不断优化组合，既使得债券投资组合有效地远离风险，又可以让投资收益趋向最大化。

1.2 线性规划

线性规划是众筹学中一个重要分支，是辅助人们进行科学管理的一种数学方法，常与数学模型有机结合，以约束条件为约束取得目标极值。在节省人力、物力与财力等资源的前提下，为战略决策的制定做出最优方案，为方案设计的制定提供科学的依据，因此线性规划普遍应用工程技术、经济管理和军事作战等诸多方面。通常情况下，使用线性规划建立数学模型的步骤：第一，归纳目标函数和约束条件；第二，在坐标系中标出已归纳好的约束条件及其约束区域；第三，计算约束区域中目标函数的最优解及其对应的最优值。

1.3 LINGO应用

LINGO是一套专门用于求解最优化问题的软件包，内置建模语言，可以用于提供多个内部函数，是集数值、符号、图形处理以及程序编码、建模设计等强大功能于一体的专用型软件，该软件由美国LindoSystem Inc.开发。主要用于求解线性规划问题和二次规划问题，尤其对求解线性方程组与非线性方程组具有较强的计算能力。

2 研究设计

2.1 数据来源

研究所采用的数据来源于2020年河北省第三届研究生数学建模竞赛B题，为了方便问题的分析，需要假设数据不存在误差，真实可靠，内容如下。

2020年，新冠肺炎全球蔓延，严重影响了世界福祉。为刺激经济发展，M国计划发行各类代号为“拯救地球”的国家紧急债券(SEB),债券到期年限有2、3、4、5、9、12、15、18、20、25年等10种，债券每年初发行，发行时间为2021年至2049年，债券每年末兑现，兑现有效截止时间为2050年。债券服务范围涵盖医药健康、交通运输、科技研发、装备制造、国民福利五大领域，债券到期后，允许债券购买者所在的地方政府收取税率不等的税收。债券类型、到期年限、收益率、税收比率等见表1。

未来教育基金会(以下称FFE)计划在2050年前(含2050年)向M国部分高等院校捐助一笔经费以帮助贫困学生。为了增加捐助金额，FFE将现有的8 000万美元资金进行债券投资，为谨慎起见，FFE委托风险机构对各类债券进行了风险等级评估，同时，FFE制定了投资要求：①医药健康债券购买金额不得少于债券购买总金额的20%，其余每个行业的债券购买总金额不得少于债券购买总金额的10%；②所购债券的平均风险等级不得低于2.5，等级数字越大风险越低；③要求所购买的债券的平均到期年限不超过10年；④要求捐助活动结束后FFE继续保留8 000万美元资金。

若SEB债券投资只允许在第一年初进行，那这些投资将分别在第2、3、4、5、9、12、15、18、20、25年收回本金和收益，8 000万美元资金如何分配，使得15个产品的总收益达到最大。

表1 各类债券及其属性

2.2 模型假设

(1)假设模型中涉及债券的风险等级、地方政府税率和到期税前收益率等本身性质是不会因为时间的变化而发生改变，上述五大类债券的收益只与现实的客观环境有关，不会因为个人的主观因素、资金量或者资金链条的变化而发生改变。

(2)假设模型中的债券投资数额不全为整数，并且可以在实数的范围内按债券的不同类型对总投资额采取不同的分配方式。

3 模型建立

3.1 决策变量定义

进行线性规划模型建立时，需先依据各债券性质表示决策变量，总结目标函数以及约束条件。为方便描述和分析，研究将三类医疗健康债券的投资金额用x1、x2、x3表示，将三类交通运输债券的投资金额用x4、x5、x6表示，将三类科技研发债券的投资金额用x7、x8、x9表示，将三类装备制造债券的投资金额用x10、x11、x12表示，将三类国民福利债券的投资金额用x13、x14、x15表示。

3.1.1 目标函数

模型中，将债券投资收益设为y，依据上述题意，各个领域的债券有着不同的风险等级和地方政府税率，交通运输领域、装备制造领域和国民福利领域的地方政府税率分别为20%、10%和30%，而医药健康领域和科技研发领域的地方政府税率为0%，由此可看出不同的债券领域有着不同的实际收益，依据题目实际情况，列出的目标函数：

y=0.0445x1+0.3989x2+2.3211x3+0.064x4+0.46616x5+2.40432x6+0.1255x7+1.8009x8+2.3211x9+0.11295x10+0.35901x11+1.85508x12+0.03115x13+0.13139x14+1.44284x15

3.1.2 约束条件

(2)分行业债券购买金额约束。中医药健康债券购买金额不得少于债券购买总金额的20%，其余每个行业的债券购买总金额不得少于债券购买总金额的10%，即x1+x2+x3≥1600，x4+x5+x6≥800，x7+x8+x9≥800，x10+x11+x12≥800，x13+x14+x15≥800。

(5)非负条件约束。即xi≥0;i=1,2,3…13,14,15。

3.2 模型计算

图1 程序输入

基于赛题分析得知，研究涉及案例的基础数据属于一般小规模问题，使用LINGO 11.0对上述线性规划模型进行求解，LINGO编程的一般步骤为：(1)确保模型正确，定义数据的类型和意义；(2)确定指标集以便于定义集合；(3)确定已知的程序变量、决策变量及其依赖的指标集；(4)正确书写目标函数和约束条件；(5)使用LINGO进行计算。对研究的LINGO编程做以下说明：软件编程以“model”开始，以“end”结束，不同的指标集用“；”隔开，LINGO中输入的初始数据即决策变量皆默认为非负实数，LINGO编程中采用的数学符号“≥”和“>”意义相同，“≤”和“<”意义也相同。研究的程序输入如图1所示，程序输出结果如图2所示。

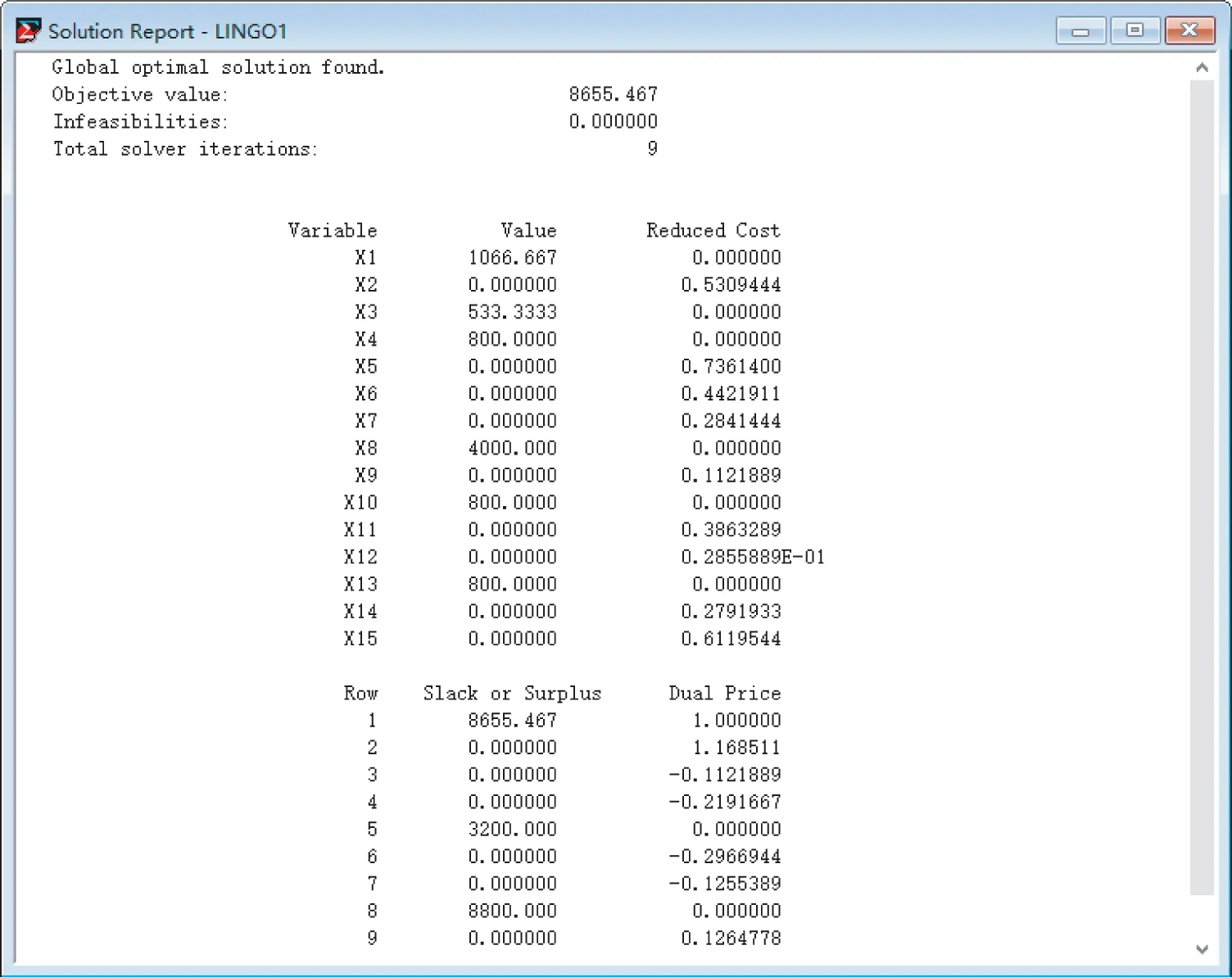
图2 程序输出结果

3.2.1 结果分析

由图2可知，LINGO经过9次迭代，求出该线性规划模型的最优解为x1=1 066.67，x2=0，x3=533.33，x4=800.00，x5=0.00，x6=0.00，x7=0.00，x8=4 000.00，x9=0.00，x10=800.00，x11=0.00，x12=0.00，x13=800.00，x14=0.00，x15=0.00，最优值为8 655.467。

以上述线性规划建模结果进行分析，若SEB债券投资只允许在第一年初进行即不进行重复投资，并且在所购债券的平均风险等级不得低于2.5，所购买的债券的平均到期年限不超过10年的情况下，分别在第2、3、4、5、9、12、15、18、20、25年收回本金和收益，想使得15个产品的总收益达到最大，则应按照如下方案进行投资：在医药健康债券领域中，到期年限为2年和20年的分别投资1 166.67万和533.33万美元，到期年限为9年的不投资；在交通运输债券领域中，到期年限为3年的投资800万美元，到期年限为12年和25年的不投资；在科技研发债券领域中，到期年限为15年的投资4 000万美金，到期年限为4年和20年的不投资；在装备制造债券领域中，到期年限为4年的投资800万美元，到期年限为9年和18年的不投资；在国民福利债券领域中，到期年限为2年的投资800万美元，到期年限为5年和18年的不投资。

若将8 000万美元按上述方式投资，可使得15个产品总收益达到最大，且最大总收益为8 655.47万美元。

4 结论与讨论

由于各资产的安全性及风险变化差异较大,因此在采用债券组合投资方案进行资产配置时，应尽力避免极端风险的发生导致资产收益损害。使用线性规划模型建立债券投资组合数学模型，再通过LINGO计算出债券组合的最优解，得到不同债券的投资分配方案，使得投资利益最大化，达到优化债券组合投资方案的目的。

通过线性规划数学建模和LINGO计算，可以找出实现利益最大化的债券组合投资方案，在软件操作上有便捷、快速和可视化等优势，可以综合考虑不同债券的信用等级、到期年限、到期税前收益等实际问题。运用线性规划理论适当设置约束条件，可以建立一个合理的债券组合投资模型，LINGO可以提高解析速度和降低求解难度，让各项数据更科学、准确，给债券投资方案设计提供新思路。需要注意的是，债券投资的收益情况受众多市场和非市场因素影响，优化债券投资方案仅是人为对投资方案预先评价和考量，以便为投资人提供债券组合投资的参考意见，所以，现实操作的债券投资实施方案还需考虑市场等诸多因素的影响，才能让投资的收益更大、风险更低。