对机场出租车司机优化配置的决策模型分析
马艳丽,左学武,褚正清
(安徽新华学院 通识教育部,安徽 合肥 230088)
0 引 言
随着经济一体化的不断发展,经济增长和居民消费水平的提升,航空运输因其高效、快捷的特点越来越受到广大居民的青睐。出租车灵活性较好,具有不定时、不定点、不定线的特点,是可以充分满足乘客个性化出行意愿的运输形式,因其安全、舒适、方便、快捷受到许多市民的喜爱,尤其是在类似机场这样人员聚集量较大的区域,相比于需要等待的机场大巴,大多数乘客更倾向于“自由”的出租车。但随着机场出租车数量的增加,出租车司机之间的竞争也越来越激烈。去指定地点排队等待接客还是直接返回市区接客,成了出租车司机决策的一大难点。在实际中,有很多影响出租车司机决策的确定和不确定因素,因此,有必要去分析研究与出租车司机决策相关因素的影响机理,利用数学模型去确定机场出租车司机的决策方案,使得总乘车效率最高,从而为出租车司机选择载客方案提供理论参考[1-9]。本文对广东机场出租车的每日载客次数、每次载客时间、载客里程和单次接单完成时间等方面展开调查,研究与出租车司机决策相关的影响机理,建立出租车司机选择决策模型,设置合适的“上车点”,以此设计出更适合出租车司机的载客方案,使得机场出租车收益尽量均衡和总的乘车效率最高。
1 问题重述
机场出租车司机优化配置的决策问题是2019年“高教社杯”全国大学生数学建模竞赛A题[10],主要考察数据处理和数据拟合等方面的能力,要求解决4个问题:(1)分析研究与出租车司机决策相关因素的影响机理,综合考虑机场乘客数量的变化规律和出租车司机的收益,建立出租车司机选择决策模型,并给出司机的选择策略。(2)收集国内某机场及其所在城市出租车的相关数据,给出该机场出租车司机的选择方案,并分析模型的合理性和对相关因素的依赖性。(3)在某些时候,经常会出现出租车排队载客和乘客排队乘车的情况。某机场“乘车区”现有两条并行车道,管理部门应如何设置“上车点”,并合理安排出租车和乘客,在保证车辆和乘客安全的条件下,使得总的乘车效率最高。(4)机场的出租车载客收益与载客的行驶里程有关,乘客的目的地有远有近,出租车司机不能选择乘客和拒载,但允许出租车多次往返载客。管理部门拟对某些短途载客再次返回的出租车给予一定的“优先权”,使得这些出租车的收益尽量均衡,试给出一个可行的“优先”安排方案。
2 模型的建立与求解
2.1 问题一模型的建立与求解
针对问题一的要求,为了分析研究与出租车司机决策相关因素的影响机理,需要考虑到出租车司机之间的竞争因素,机场优惠政策及出租车公司的优惠政策,特殊的天气情况对出租车司机的影响和出租车行驶速度不同以及单次载客人数不同对出租车的收益影响,还需要考虑到乘客上车时间的间隔和各车型每公里耗油量的不同,利用层次分析法建立系统的递阶层次结构(图1)。
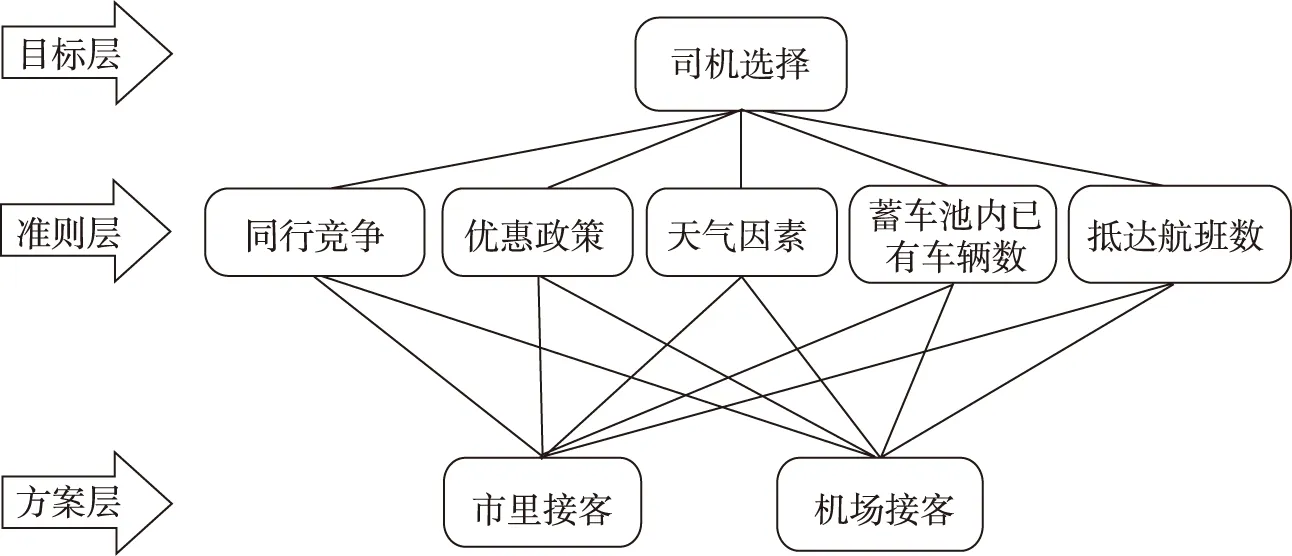
图1 影响出租车司机决策的因素
除此之外,还需要研究机场乘客数量的变化规律,根据国家统计局公布的数据得到了2018年机场每月的客流量情况和不同时间段的客流量情况(表1~2)。
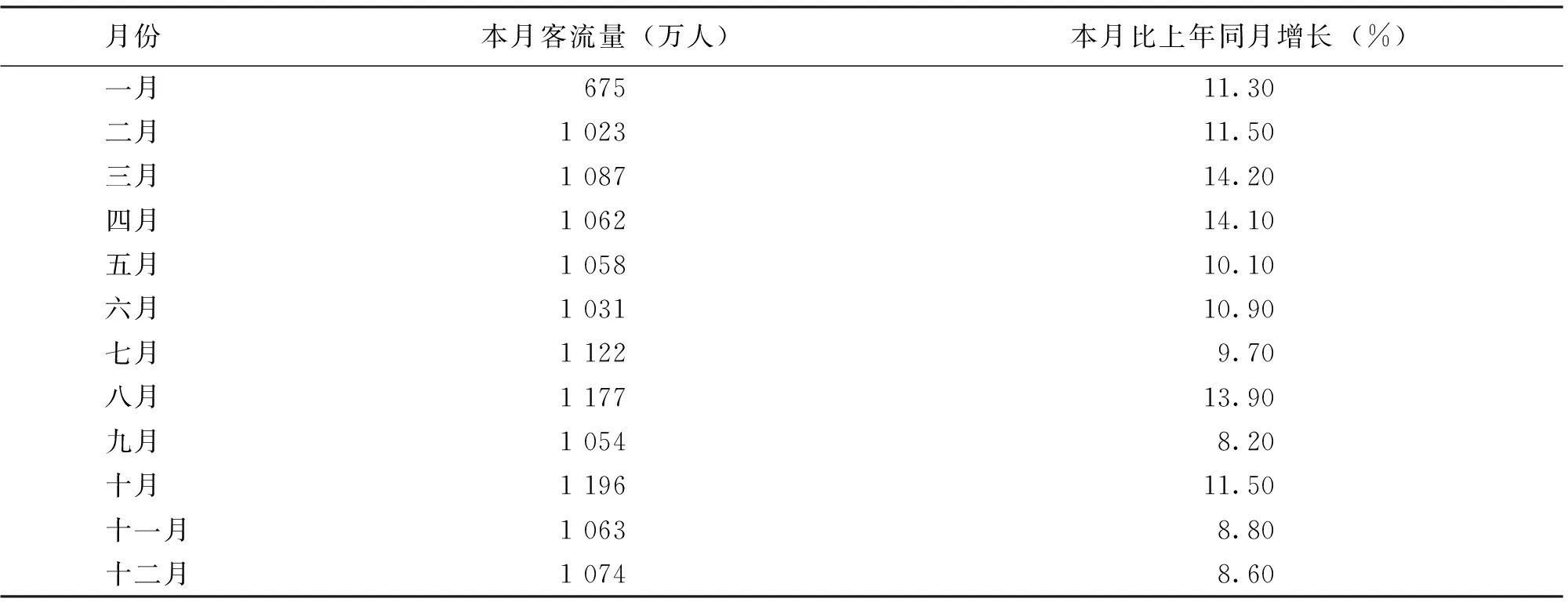
表1 2018年机场平均每月客流量
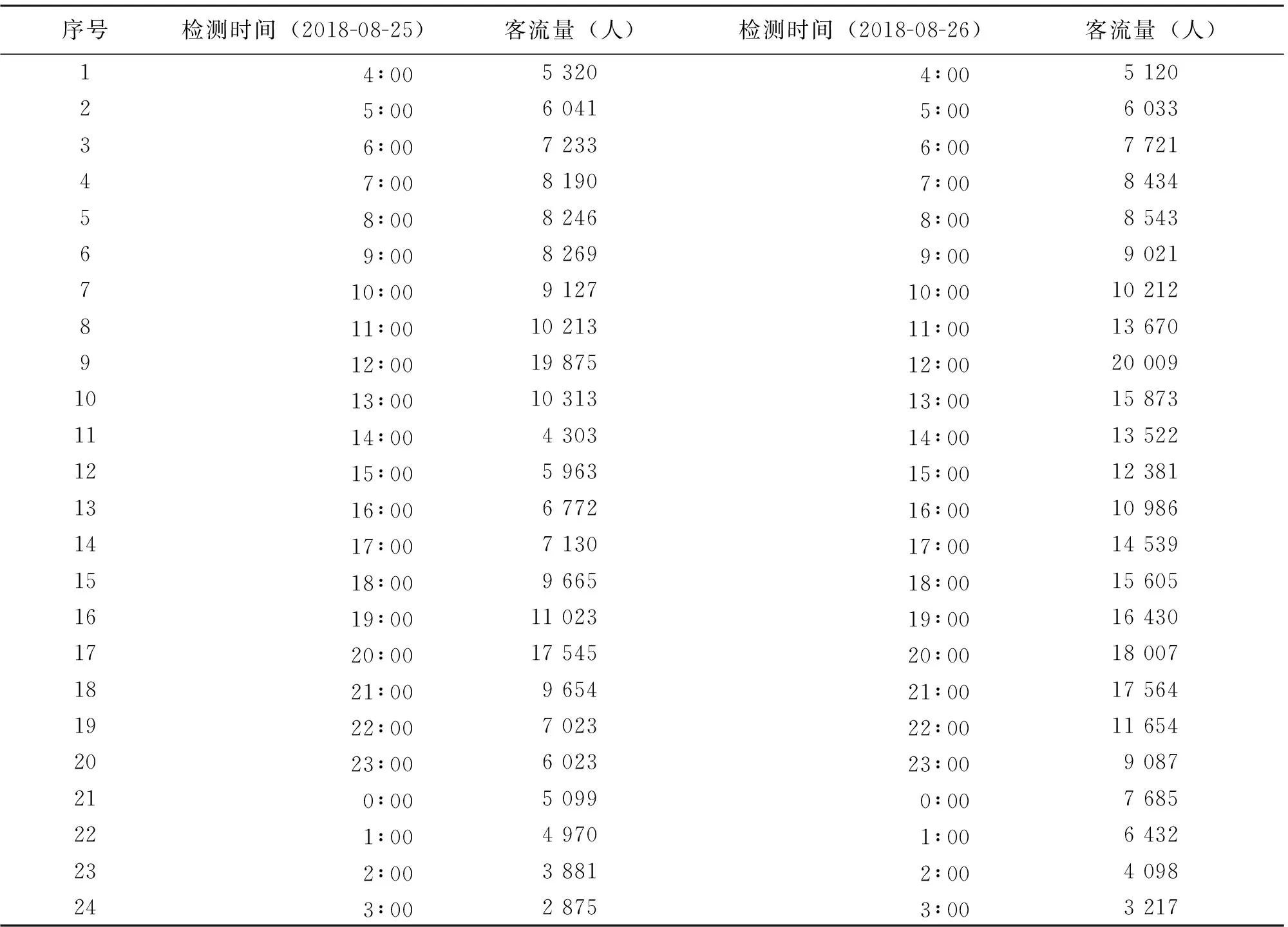
表2 机场航站楼不同时间段的客流量
由表1可知,一年中的月机场客流量趋于平和,但在夏季和秋季会呈现一定的增长趋势,由于开学季和国庆的来临,8月和10月的客流量比其他月份的客流量多,是一年中客流量最高的月份,机场客流量具有一定的趋势向和周期向。为了更直观地反应一天内的客流量变化情况,利用EXCEL和SPSS对表2中的数据进行了图形化处理,得到8月25日和8月26日2天的客流量随时间变化的条形统计图和折线统计图(图2~4)。
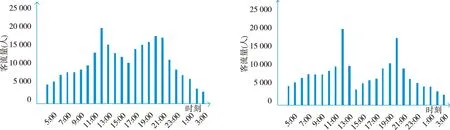
图2 8月25日客流量与时间的关系 图3 8月26日客客流量与时间的关系
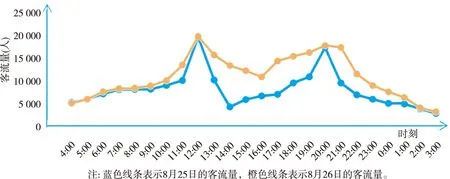
图4 8月25日和8月26日客流量与时间的折线统计
根据问题一的要求,为找出更加合理的机场出租车司机的选择方案,收集了某出租车100 d的相关信息情况,部分天数的具体数据见表3。
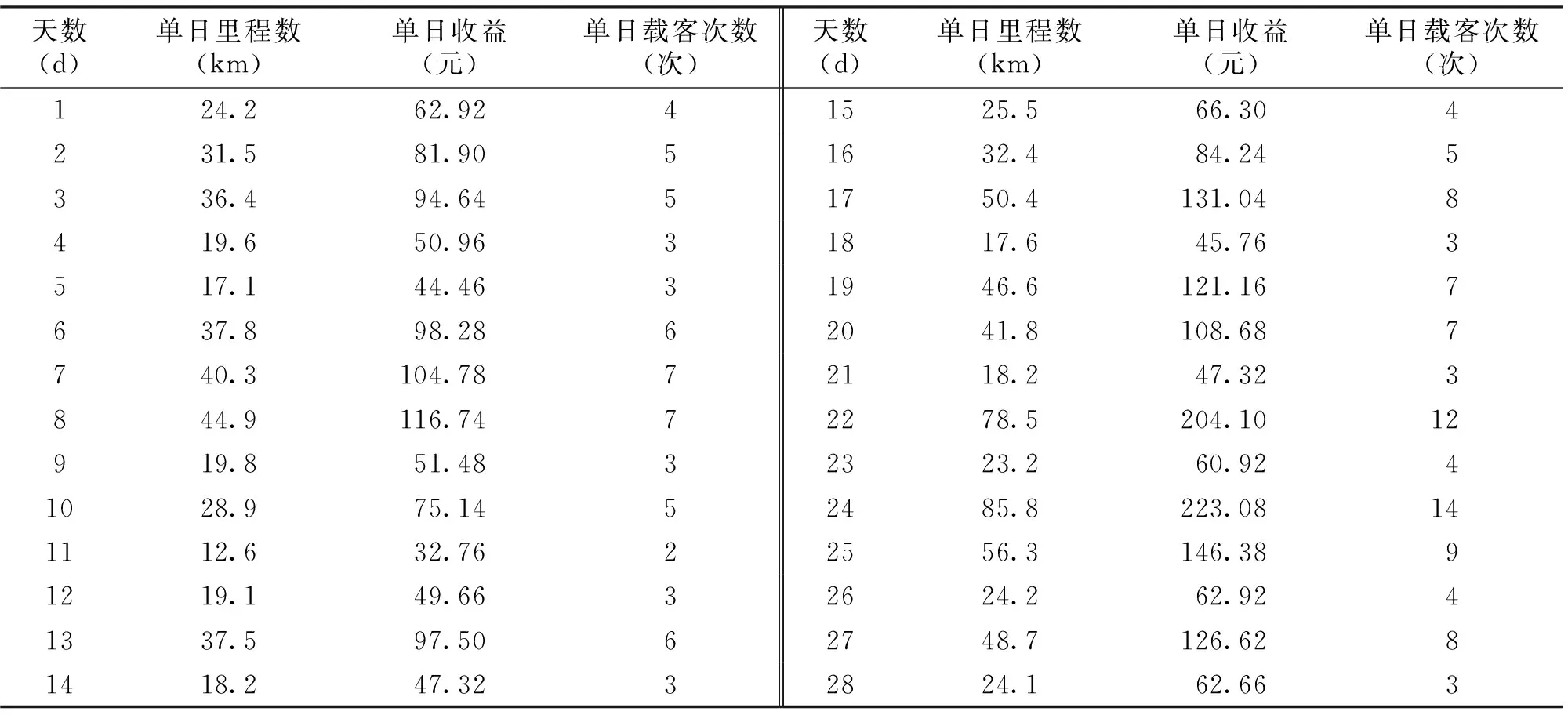
表3 某出租车部分天数的信息情况
利用MATLAB,采用多项式的拟合方式,得到单日出租车司机收益z,单日载客里程数x和天数y之间的函数关系式
z=f(x,y)=a0+a1x+a2y+a3x2+a4xy+a5y2+a6x3+a7x2y
+a8xy2+a9y3+a10x4+a11x3y+a12x2y2+a13xy3
(1)
其中,a0=3.905,a1=2.535,a2=5.853,a3=0.0331,a4=-1.189,a5=3.09,a6=-0.00034,a7=0.0009,a8=0.104,a9=-0.205,a10=-1.105×10-6,a11=6.734×10-5,a12=-0.00072,a13=-0.0003,R2=0.224,并给出相应的拟合曲面图(图5)。
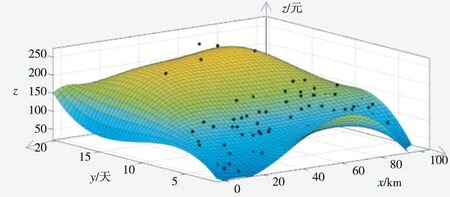
图5 单日出租车司机收益、单日载客里程数和天数的拟合曲面
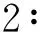
2.2 问题二模型的建立与求解
根据问题二的要求,需要收集国内某一机场出租车的相关数据,并给出该机场出租车司机的决策方案。根据文[11]提供的数据,得到广东某机场部分出租车平均每日载客收益、载客次数和等待时间等相关数据(表4)。
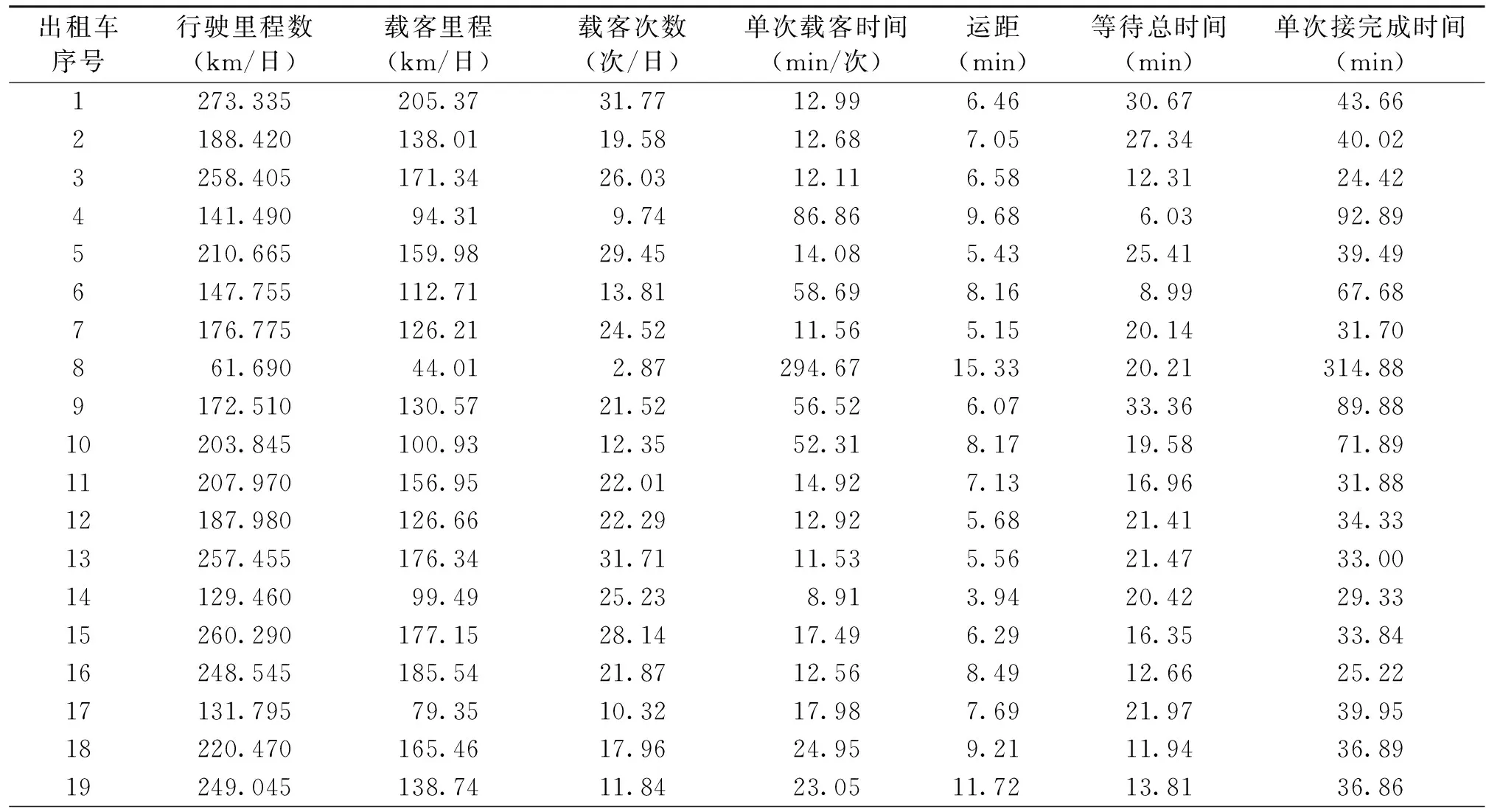
表4 广东某机场出租车相关信息
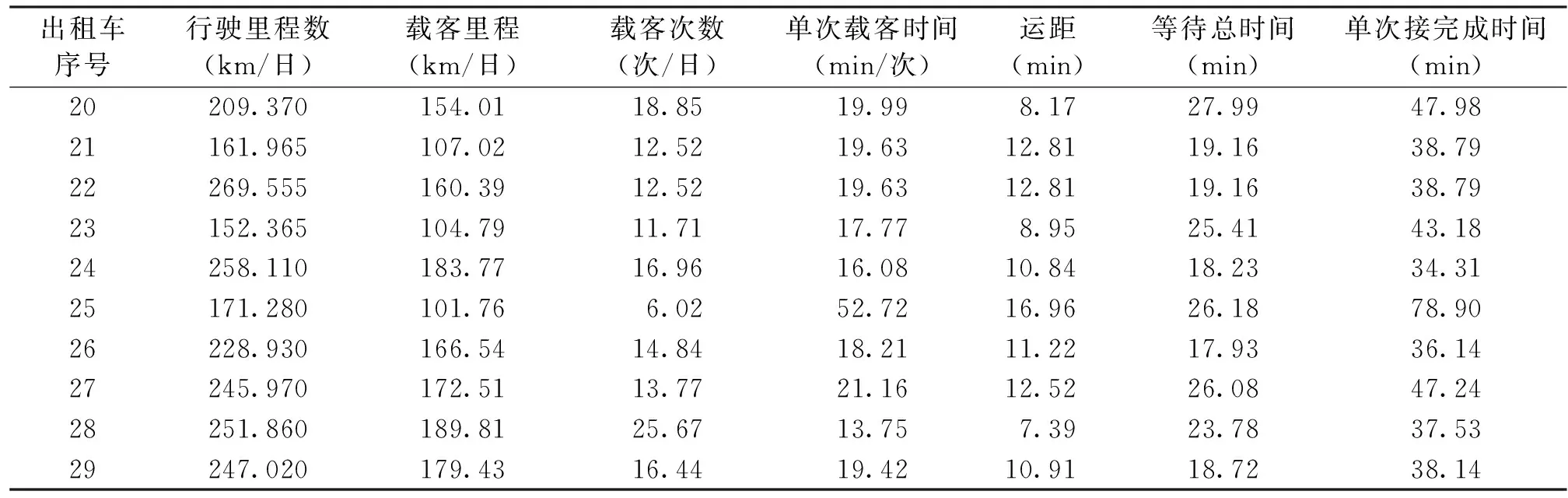
表4(续)
为了找出适合该机场出租车司机决策的最佳方案,首先,分析单日出租车司机收益与等待时间之间关系,根据表4提供的数据,利用MATLAB,并采用高斯逼近的拟合方式,得到单日出租车司机收益ω和等待时间t的具体表达式
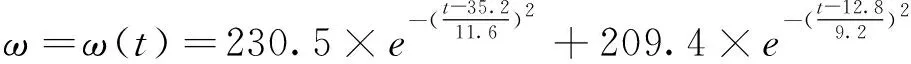
(2)
得到相应的拟合曲线图(图6)。
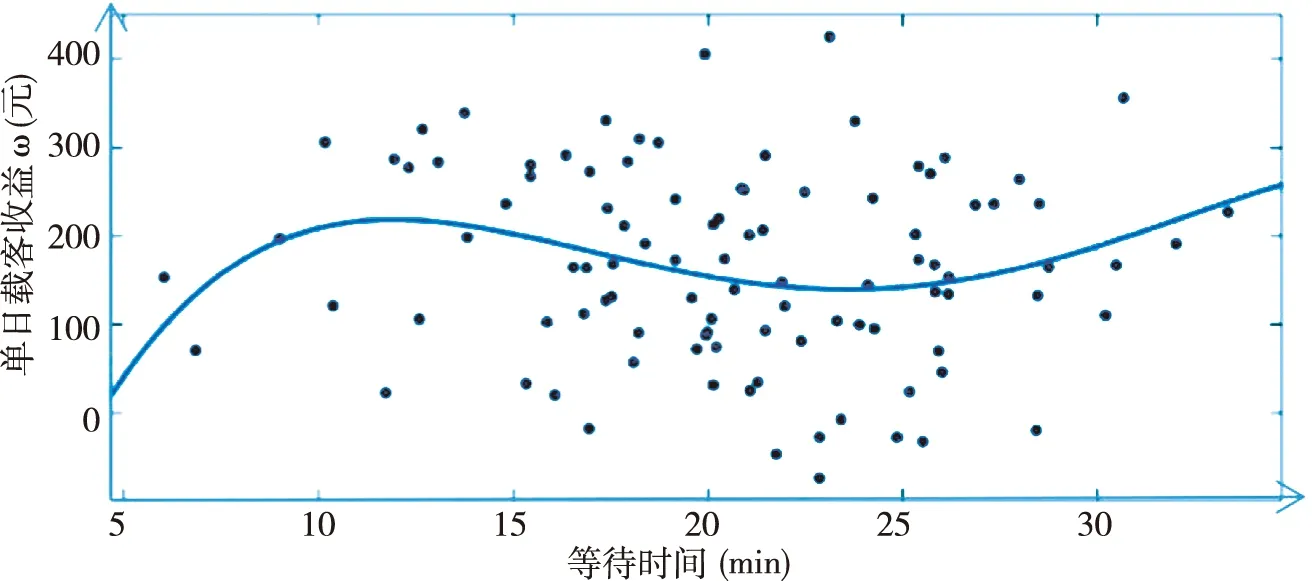
图6 单日载客收益和等待时间的拟合关系
由图6可知,曲线整体呈现先上升再下降再上升的趋势,总体变化趋势较平稳。出租车司机等待时间为5~25 min时,出租车司机单日载客利润的趋势为先上升后下降。等待时间在25~35 min时,出租车司机单日载客利润的趋势又由下降转为上升。表示在一定范围内单日载客利润随等待时间的增加而增加,达到某固定值之后单日载客利润随等待时间的增加而减少,下降到一定范围后又会增加,出租车司机的第一次收益高峰出现在10 min附近,出租车司机第二次收益高峰在35 min左右。符合现实生活中的基本情况。
其次,讨论单日载客收益与单日载客里程数之间的变化规律,根据表4提供的数据,利用MATLAB,采用三次多项式的拟合方式,得到单日载客收益ω和单日载客里程数θ的函数关系式
ω=ω(θ)=c0+c1θ+c2θ2+c3θ3
(3)
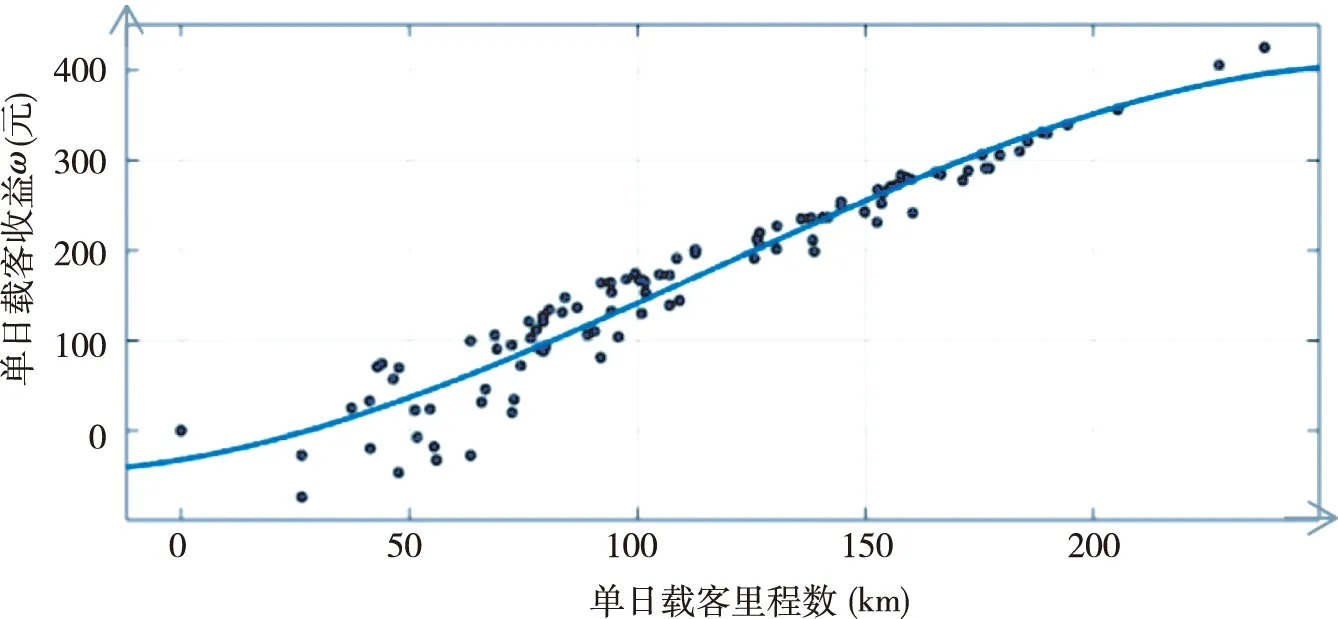
图7 单日载客收益和载客里程数的拟合
其中,c0=-32.21,c1=0.843,c2=0.013,c3=-3.57×10-5,得到相应的拟合曲线图(图7)。
由图7可知,机场出租车单日载客利润和单日载客里程数呈正相关。单日载客利润随着单日载客里程数的增加而增加。单日载客里程数越多,单日载客利润越大。
最后,为了进一步分析单日载客利润与单日载客次数和等待时间的关系,利用MATLAB,采用五次多项式逼近方式,得到单日载客收益ω与单日载客里程数θ和等待时间t的函数关系式
ω=ω(t,θ)=b0+b1t+b2θ+b3t2+b4tθ+b5tθ2+b6t3
+b7t2θ+b8tθ2+b9θ3+b10t4+b11t3θ+b12t2θ2+b13tθ3
+b14θ4+b15t5+b16t4θ+b17t3θ2+b18t2θ3+b19tθ4,
(4)
其中,b0=428.4,b1=-10.49,b2=-61.43,b3=0.17,b4=0.53,b5=5.39,b6=-0.0013,b7=-0.006,b8=-0.038,b9=-0.244,b10=3.47×10-6,b11=2.47×10-5,b12=-1.83×10-4,b13=2.05×10-3,b14=4.14×10-3,b15=-1.28×10-7,b16=8.97×10-7,b17=-1.85×10-6,b18=-2.25×10-5,b19=-1.98×10-5,并得到相应的拟合曲面图(图8)。
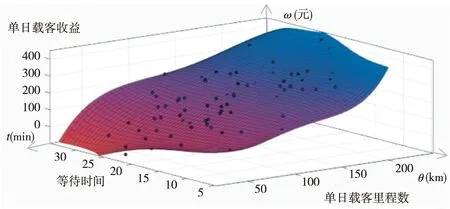
图8 单日载客收益与单日载客里程数和等待时间的关系
由图8可知,机场出租车单日载客收益与机场出租车单日载客里程数呈正相关,与出租车等待总时间成负相关,机场出租车单日载客里程数越多,等待时间越短,单日载客收益越大。
2.3 问题三模型的建立与求解
结合实际情况,航空枢纽中常见的离港出租车上客系统主要有单车道、多车道(矩阵式)、斜列式3种,本题采用多车道中的双车道情况,需要分别考虑停车泊位的多少和上车点的分布对乘客乘车效率的影响。运用控制变量法,先控制“上车点”不变,讨论两条并行车道停车泊位的最佳数量,再控制停车泊位的数量不变,讨论“上车点”位置的不同对乘车效率的影响。结合以上讨论,得出最佳停车泊位和最佳上客点的分布情况。
首先,设置泊位供乘客上车,分别给予编号。构建矩阵式出租车上客系统,该系统需要分别控制车辆放行和乘客放行,为了保证上车乘客的人身安全,采用分批次的方法,保证“乘车区”内所有车辆均离去后,再开始进行下一批次的车辆的放行,当“乘车区”所有泊位都被占用时,停止本批次的车辆放行。当出租车到达泊位时,机场管理人员开始放行相应数量的乘客进入“乘车区”。当“乘车区”内的车辆全部驶离后,系统开始下一轮模拟。利用模型仿真预估乘客从乘车区乘车驶离的时间,根据时间长短,判断最佳的停车泊位数量。根据上述分析,结合实际情况,建立以下几种设计方案(图9~12)。
(1)“上车点”固定,设立4个停车泊位。
(2)“上车点”固定,设立6个停车泊位。
(3)“上车点”固定,设立8个停车泊位。
(4)“上车点”固定,设立10个停车泊位。

图9 4个停车泊位
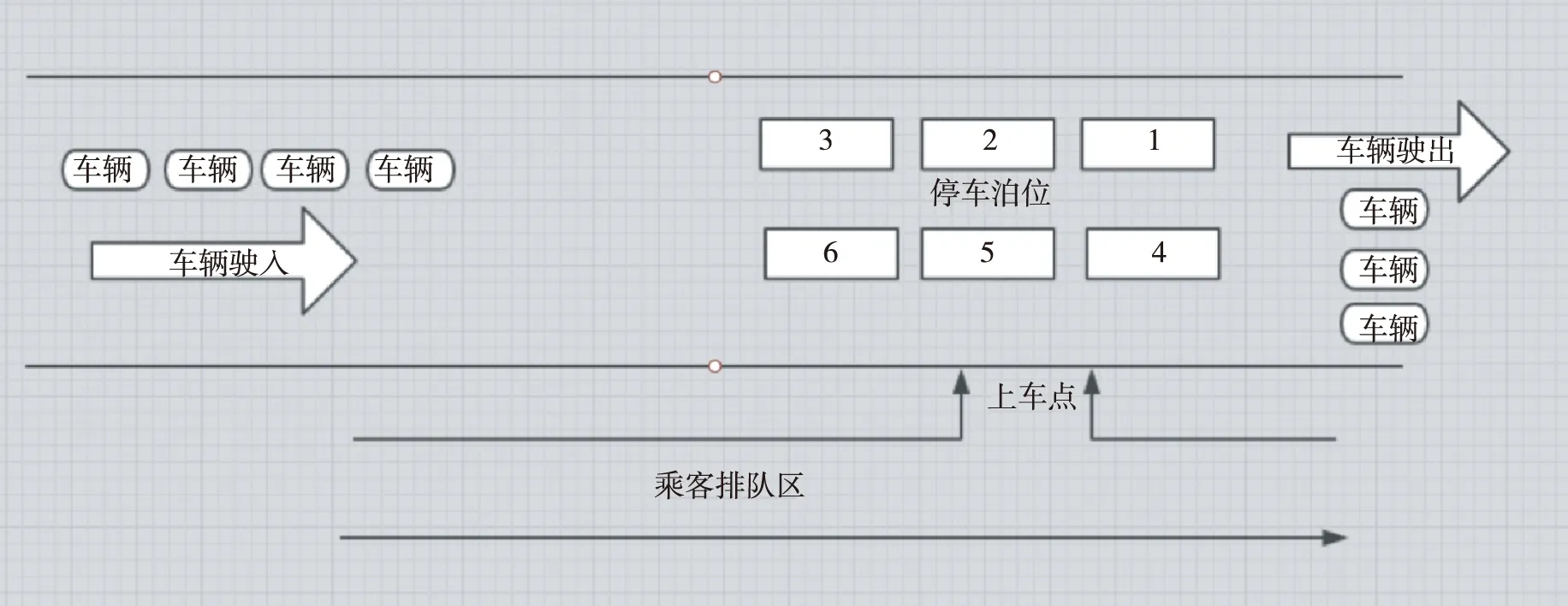
图10 6个停车泊位
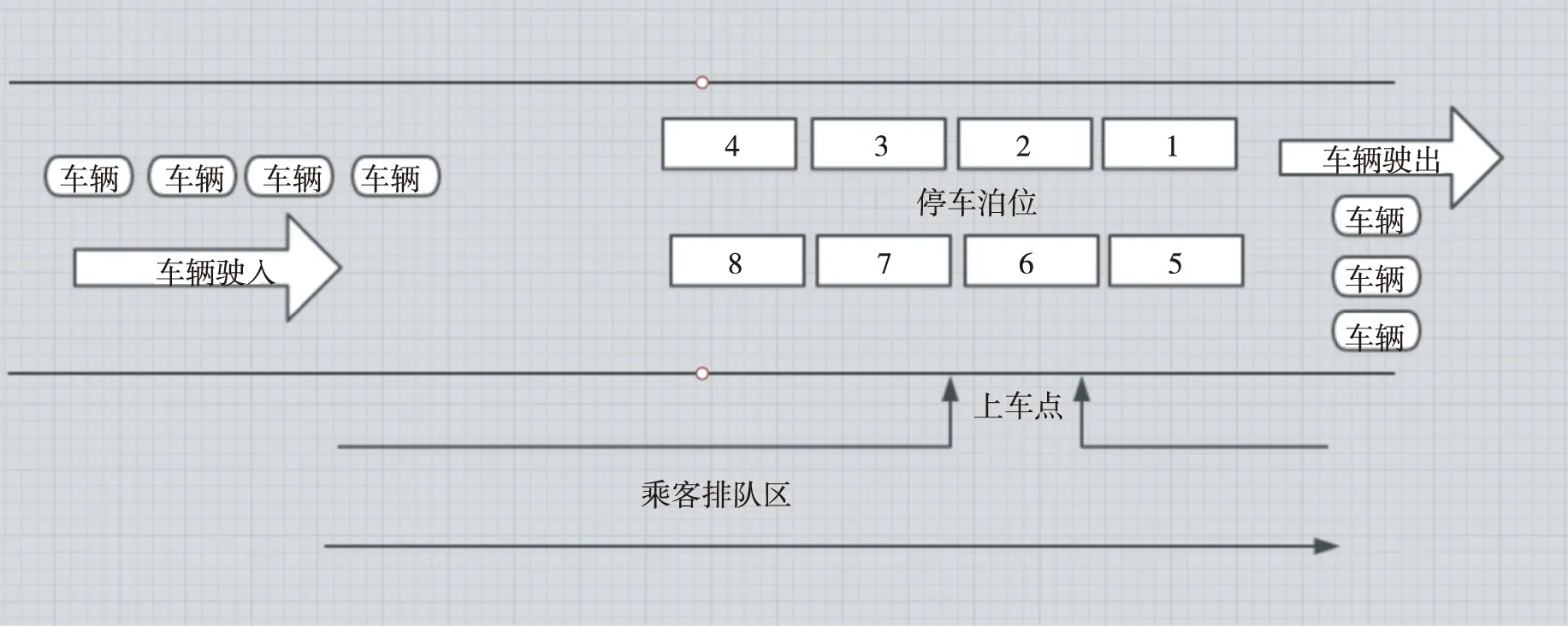
图11 8个停车泊位
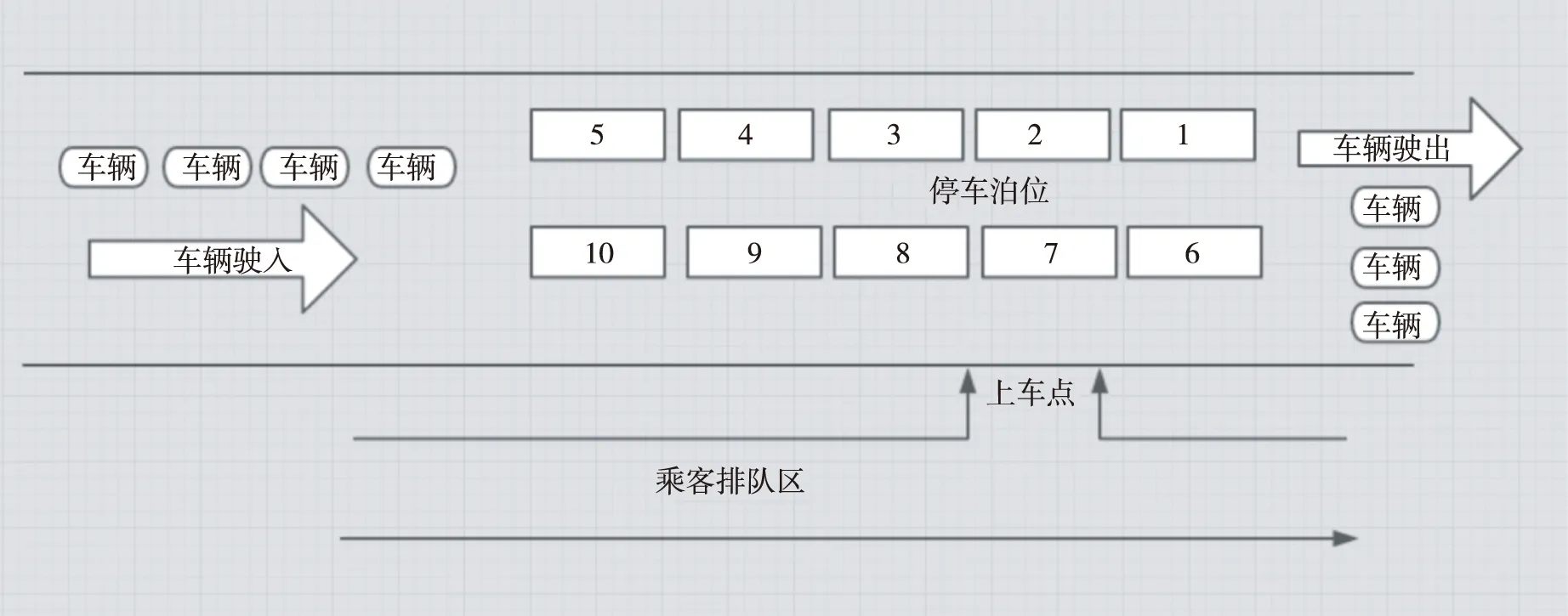
图12 10个停车泊位
在矩阵式出租车上客系统中,只有在最前面的出租车驶离后,后面的出租车才能“串行”驶离。利用计算机模拟1 000辆出租车的通过时间,仿真模型在第86 494 s结束,期间共通过出租车10 000辆,可得表5所示的结果。
通常情况下,出租车在驶离过程是“串行”的,在前面的出租车未驶离泊位之前,后面的出租车无法驶离,考虑到“乘车区”的公共秩序及乘客行走距离所需要的时间,泊位数应当控制在一定范围内,研究发现,当泊位数量超过8个时,车道系统的通行效率会有所下降。
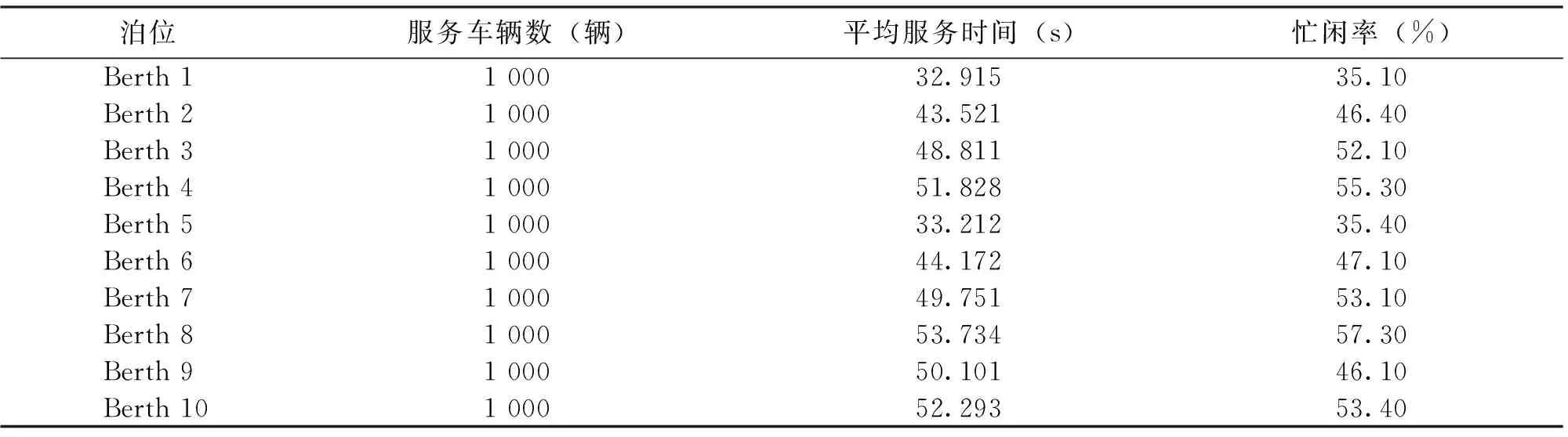
表5 计算机模拟的出租车信息
由表5分析可知,当“上车点”一定时,设立8个停车泊位忙闲率最高,即通行效率最高。通过上面的分析可知,设立8个停车泊位时通行效率最高。
接着,固定最佳数量的停车泊位,分配上车点,由一般停车泊位数量可知,两条并行车道最多有2个上车点,在此基础上分2种可能,一种是2个上客点分布在同一边的不同位置,根据模型中的数据得出一批车辆从进入到离开所需的总时间。第二种是2个上车点分布在不同侧,同理,根据数据计算同一批车辆从进入到离开所需的总时间,再根据2种不同上客点分布所需时间,对比效率,即可得出最佳停车泊位和最佳上车点的分布情况。结合实际情况可知,机场“上车点”一般不超过2个,可设计为以下3种情况(图13~15)。
(1)只有1个“上车点”。
(2)有2个“上车点”且分布在同一边的不同位置。

图13 “单上车点”
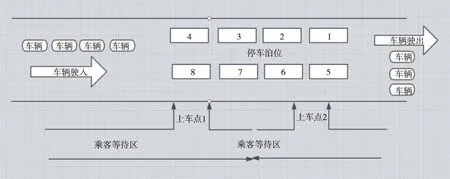
图14 分布在同一边的不同位置的“双上车点”
(3)有2个“上车点”且分布在不同侧。
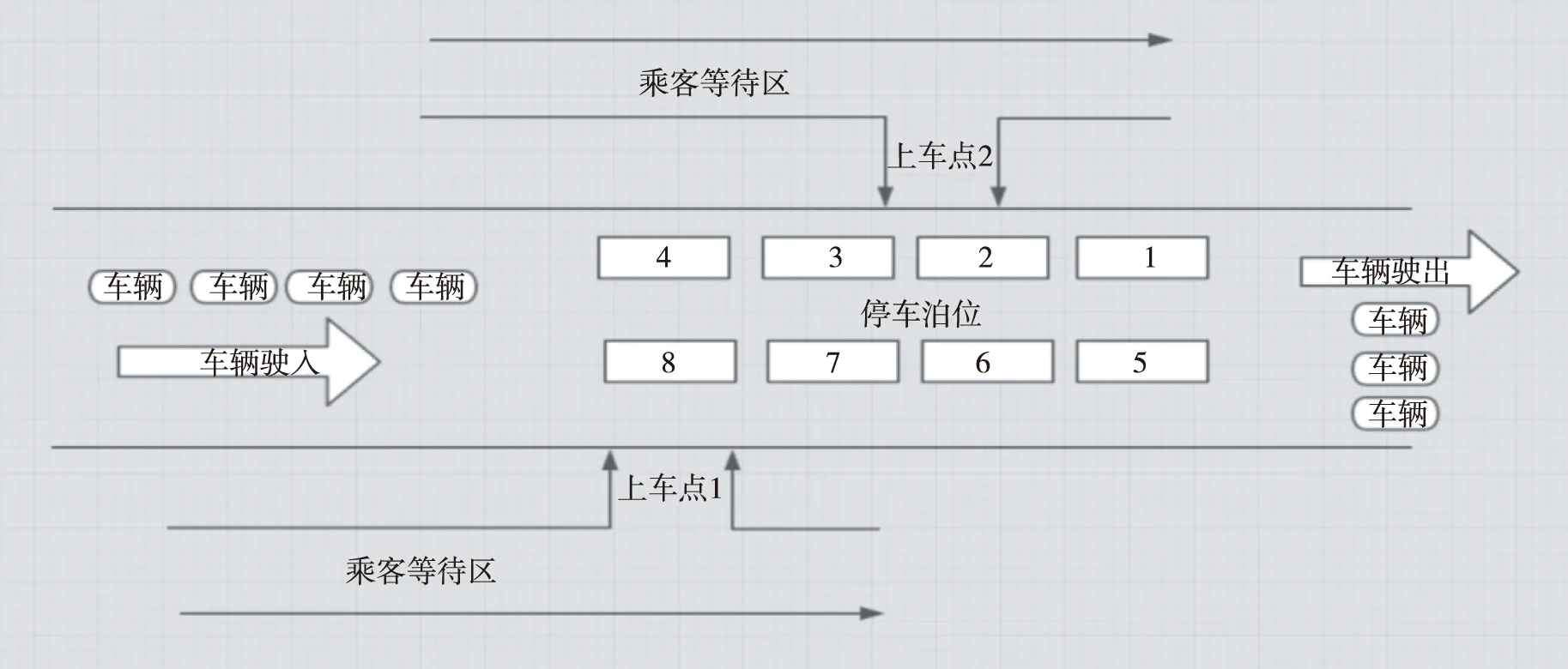
图15 分布在不同侧的“双上车点”
“单上车点”适用于小型机场,客流量和出租车数量较少,很大程度上节省空间。但如果在中大型机场时,由于客流量较大,时常会出现出租车“串行”的情况,车辆在驶离过程中相互耦合的情况比较严重,容易造成机场交通堵塞,机场体验感较差,不利于乘客的出行。为了疏通机场乘客,机场管理人员通常会选择增加泊位数,但当泊位数超过8个时,机场出租车的通行效率会有所下降,且现场秩序难以维持,给机场的管理带来一定的挑战。为了验证两种“上车点”的通行效率,利用计算机建立仿真模型,得到1 h内通过“单上车点”和“双上车点”的出租车数量(表6)。
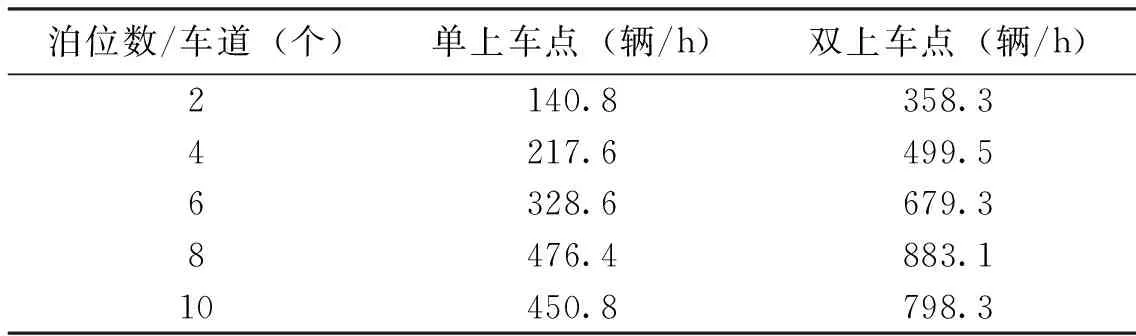
表6 “单上车点”和“双上车点”的相关数据信息
同侧“双上车点”和两侧“双上车点”可以在一定程度上缓解机场客流量的压力,通行效率较单上车点明显提高,满足较大的客流量的需求,还可以在一定程度上缓解驶离车辆之间的相互耦合,保证乘客的安全。原则上来说,同侧“双上车点”比两侧“双上车点”节省了“乘客等待区”的占地面积,适用于占地面积少但客流量大的机场。长远而言,两侧“双上车点”更具有发展前景,且“乘客等待区”的占地问题,可以通过建立新的模型来解决(图16)。
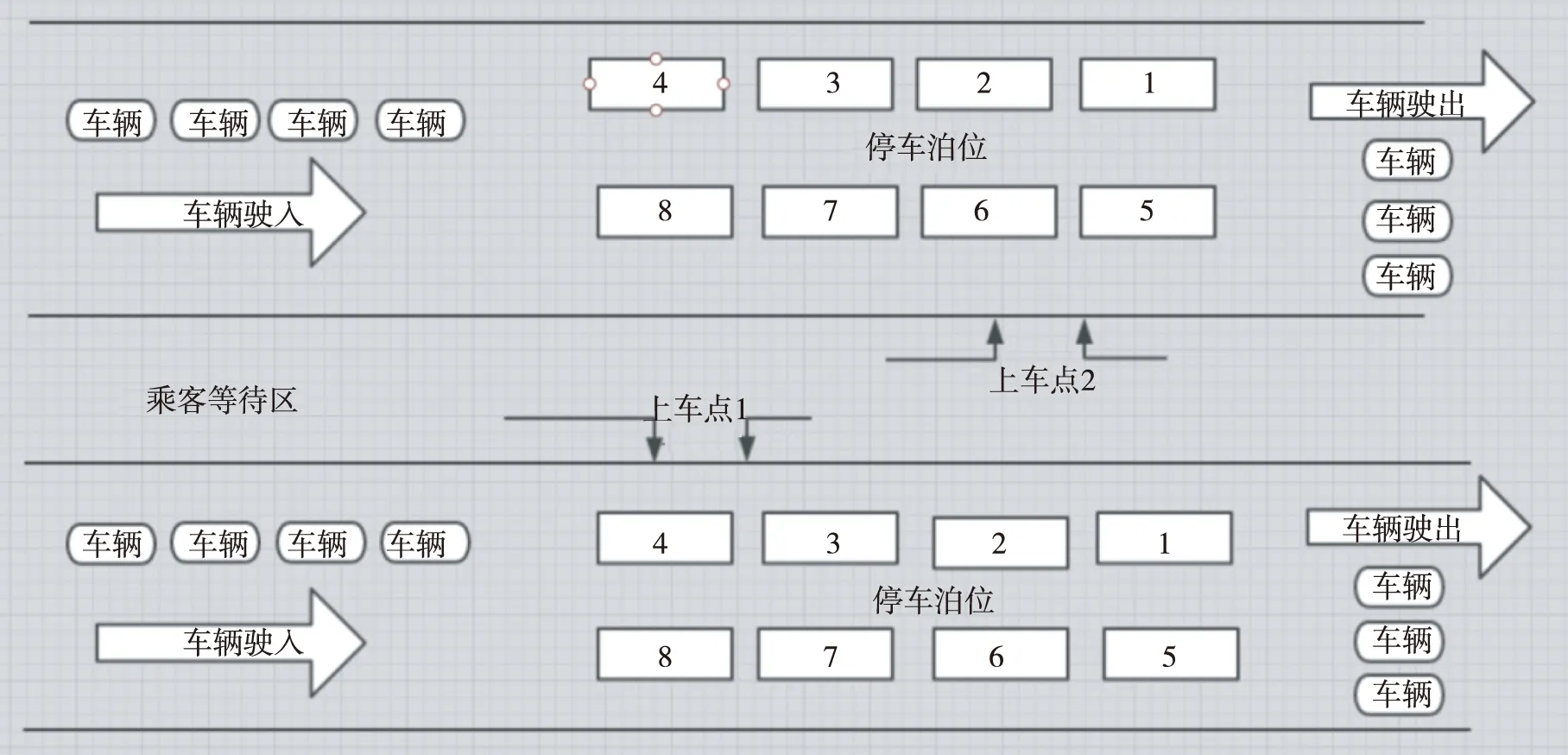
图16 “乘客等待区”的共用情况
此模型通过适当扩大“乘客等待区”的规模,实现“乘客等待区”的共用,对机场规模的扩建和长远发展,具有一定的理论参考意义。
2.4 问题四模型的建立与求解
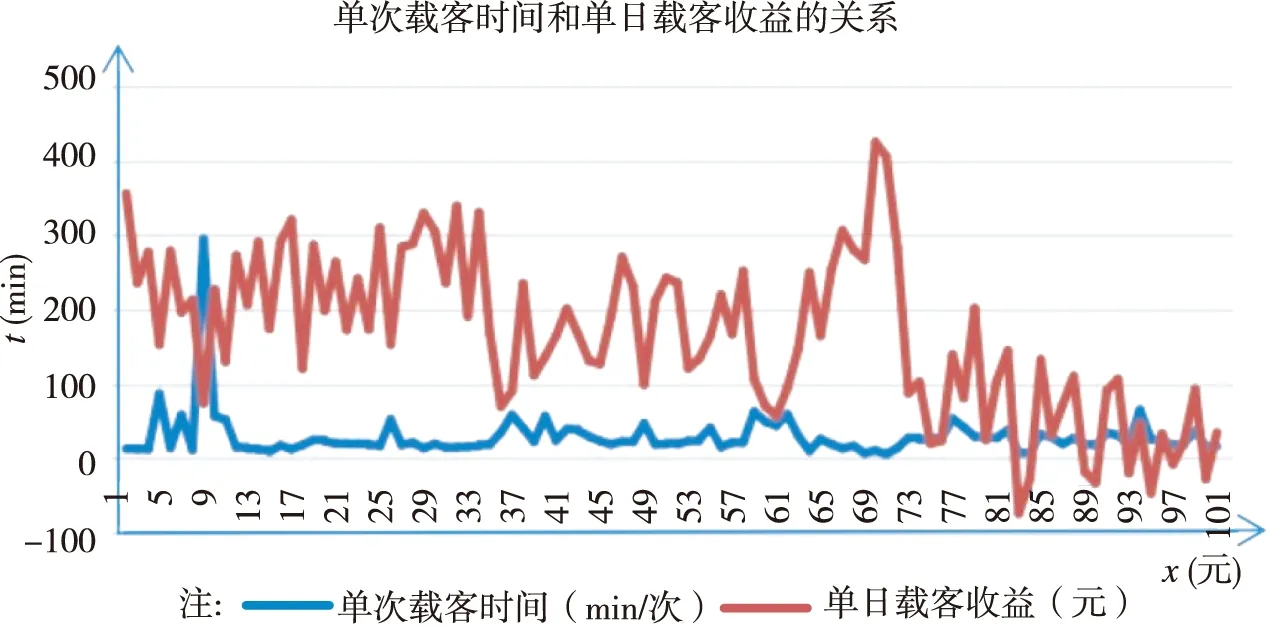
图17 载客收益与载客时间的关系
根据问题二的分析可知,机场出租车载客收益与载客所行驶的里程数有关,载客行驶的里程数越大,机场出租车司机的收益越大。根据模型假设,出租车速度是一定的,因此只需要研究出租车司机收益与载客时间长短之间的关系。为了更直观地反映出租车司机收益与载客时间长短之间的变化规律,利用SPSS得到出租车司机收益与载客时间长短之间的关系折线图(图17)。
对于问题四,需要建立“可行”方案使短途载客的出租车司机收益与长途载客的出租车司机收益尽量均衡。根据模型中的数据,将载客时间长的数据和载客时间短的数据分别筛选出来,并求出平均值20.029 min。在出租车速度恒定的条件下,出租车司机每次载客的平均时间接近20 min,以平均载客时间为分界点,单次载客时间低于20 min称为短途,单次载客时间高于20 min称为长途。
为了使机场出租车司机的收益均衡,可以在机场开辟一条短载出租专用道(图18),根据载客时间的平均值大小,得到短途出租车司机需在往返40 min之内进入短途专用车道。
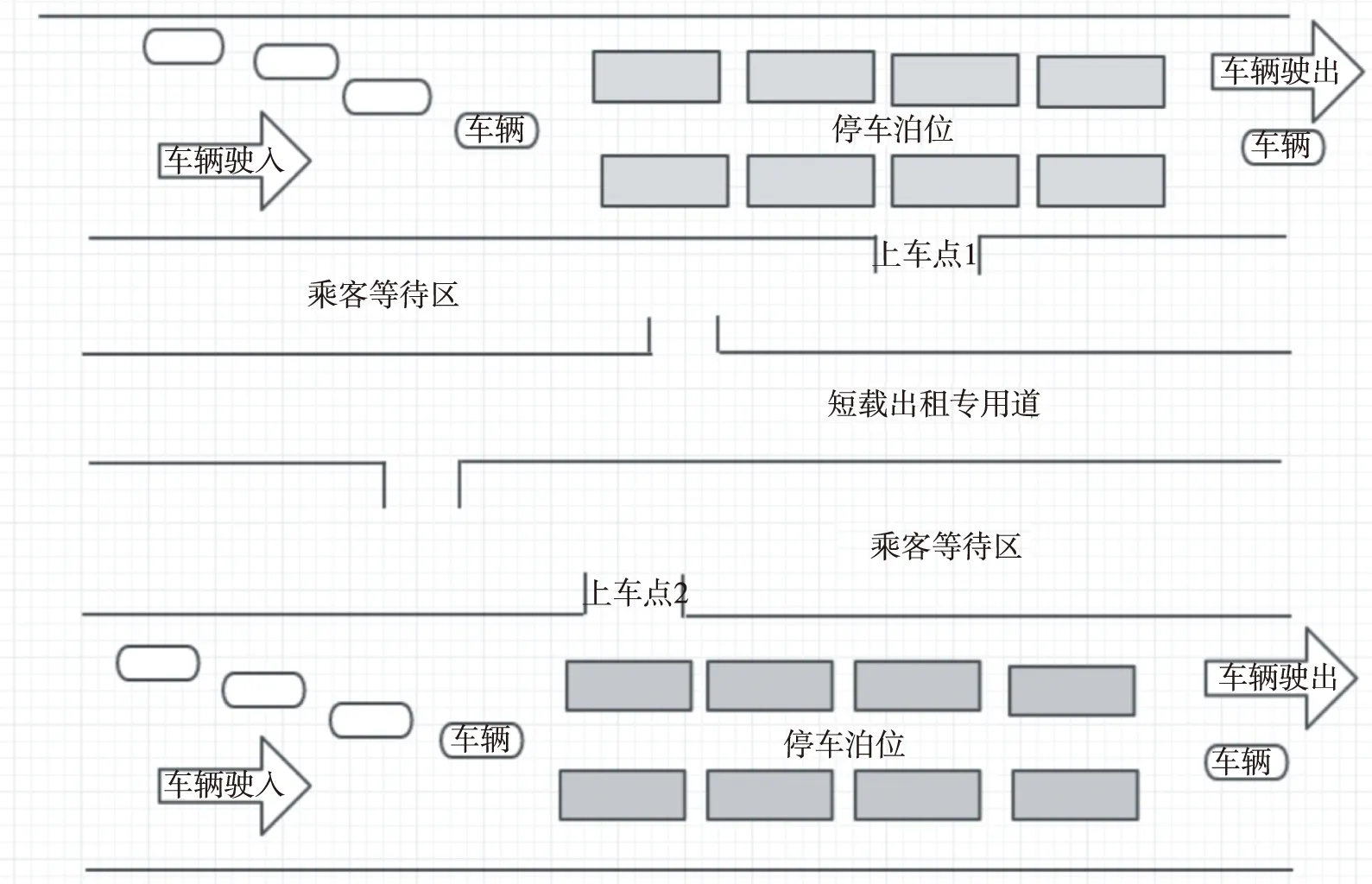
图18 短载出租专用道
由于开辟的短载出租车专用道是单行道,单车道出租车上客系统的通行效率较低,时常会出现出租车“串行”的情况,车辆在驶离过程中相互耦合的情况比较严重,容易造成机场交通堵塞。为了保证短载出租车专用道的畅通,根据不同泊位数与通行能力之间的关系,需要计算出其最佳停车泊位的数量(表7)。
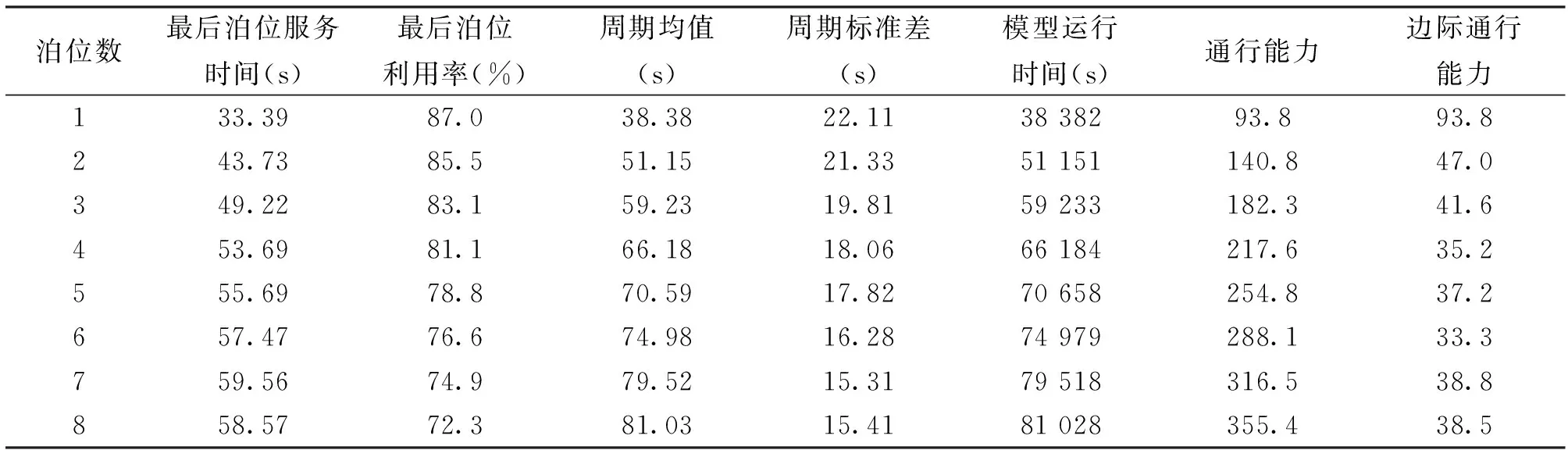
表7 不同泊位数与通行能力关系汇总
由表7可知,短载出租专用道的出租车上客系统,随着泊位数量的增加,通行效率不断增加,但增长率成下降趋势,考虑到“乘客等待区”的秩序及乘客的行走距离,泊位数最好不超过6个;当泊位数为5个时,通行效率为每小时254.7辆,当泊位数为6个时,通行效率为每小时288.1辆。
综合表7和图18可知,管理部门对某些短途载客再次返回的出租车给予一定的“优先权”时,机场出租车司机在载客往返时间不超过40 min时,可以进入短途专用车道,进行载客。考虑到泊位利用率和“乘客等待区”秩序问题,短途专用车道的管理人员可控制每次进入短途专用车道的车辆数不超过6个。
3 结论与讨论
出租车是机场大多数乘客到达目的地所使用的主要交通工具之一,在实际中,有很多影响出租车司机决策的确定和不确定因素。为了分析研究与出租车司机决策相关因素的影响机理,本文利用数学模型来确定机场出租车司机的决策方案,根据时间长短,判断最佳的停车泊位数量。运用控制变量法,得出最佳停车泊位和最佳上客点的分布情况,使得总的乘车效率最高。在这个追求“快”速度的时代,高效的乘车速度会给人们带来很大的收益。本文对机场出租车问题进行研究所得到的模型也可以进行推广使用,如机场大巴收益情况。

