产业结构、人口结构与居民消费结构耦合协调的经济增长效应

王良虎 王 钊

一、引言

改革开放以来，中国经济经历了40 年高速发展，被称为“中国奇迹”，但同时经济结构也发生较大变动，据国家统计局数据显示，第一、二、三 产 业 占 比 由 1992 年 的 21.78% 、 43.45% 、34.76%，变为至今的7.9%、40.5%、51.6%。产业结构发生较大变化，但较发达国家而言，我国产业结构还有待进一步优化升级。随着我国经济社会的发展，我国居民消费结构、人口结构均发生较大变化。首先，消费结构不断优化。具体表现为城镇居民用于食品和衣着消费占总消费的比例由1992 年的66.94%，下降到2018 年的34.9%，而交通、文教、医疗的消费占比由1992 年的13.95%增加到2017 年的33.2%，消费结构逐渐由吃穿为主的生存型消费转变为享受型、发展型消费。但就目前而言，衣、食、住、行消费支出仍是当前城乡居民消费的主要部分，2017 年城镇和农村居民食品、衣着、居住、交通通信四类消费支出占人均总消费的比例分别达到71.8%和71.3%，消费层级依然偏低。其次，我国人口在总量、分布、素质以及性别结构等方面均发生了较大变化。第六次全国人口普查的相关数据显示，2017 年总人口为13.9 亿人，男性占比为51.17%，女性占比为48.83%，65 岁及以上人口为1.58 亿人，较上一年增加了0.08 亿人， 由此表现出我国“人口红利”逐渐消失，逐步进入老龄化社会。因此，在面临在产业结构、人口结构及居民消费结构亟待进一步优化调整的现实背景下，三者作为经济增长的重要保障，三者的协调发展必然对经济高质量增长产生重要影响。那么目前三者之间协调发展水平究竟如何？时空演变又具有什么样特征？对经济高质量增长的影响具体又是怎样的呢？通过对以上问题的深入研究将为我国经济转型发展提供较为重要的政策启示。

二、文献综述

产业结构优化调整提高了资源的有效利用率，由此改善生产效率，因此当前国内外学者将产业结构变迁作为经济增长的重要来源进行了深入研究。关于产业结构演变对经济增长具有显著推动作用的研究可追溯到上世纪60年代。Chenery（1960）[1]通过构建多国模型对51 个国家进行了研究，认为产业结构调整而产生的“结构红利”是促进经济增长的最终原因。Rostow（1960）[2]的主导产业扩散理论与经济增长理论，阐明了主导产业对经济增长的带动作用。Cimoli（2011）[3]对金砖四国之间的经济发展历程进行了对比分析，并得出四国产业结构的演变有利于各国的经济增长。较国外来说，我国关于产业结构与经济增长之间关系的研究相对较晚。杨治（1985）[4]首次在其著作当中论述了产业结构的演变规律与经济发展内在的均衡问题。随着研究的不断深入，越来越多的学者认识到了产业结构对经济增长的重要性。干春晖等（2011）[5]基于我国省级的面板数据，从产业结构高级化和合理化两方面考察了产业结构演进对经济增长的影响，并得出结论，随着时间的推移，产业结构高级化对经济增长的促进作用逐渐变小，而产业结构合理化则对经济增长的作用逐渐增强。谢婷婷和潘宇（2018）[6]基于空间计量模型研究了我国30 个省（区、市）的产业结构升级与经济增长之间的内在关系，认为产业结构升级对现阶段我国经济发展具有显著的正向作用，并对邻近地区具有较强的辐射作用。而张永安（2019）[7]研究发现产业结构促进作用存在边际效应递减规律。部分学者认为产业结构调整对经济增长并非表现出线性关系，如李村璞（2018）[8]使用非线性平滑转换模型研究了产业结构与经济增长之间的非线性关系。杨占锋（2019）[9]将成渝经济区作为研究对象，定量研究了成渝经济区经济增长的产业结构变迁效应，分析表明经济增长的不同阶段的产业结构效应存在明显差异。为了进一步分析产业结构与经济增长之间的关系，需要根据不同的经济社会环境进行针对性分析，例如孙皓和石柱鲜（2011）[10]基于行业劳动力比率的视角分析了我国产业结构对经济增长的影响。高铁梅等（2018）[11]采用面板数据广义矩模型实证检验了适度城镇化、产业结构调整与经济增长的关系，研究发现产业结构调整在不同规模城市中的产出存在明显的差异。

关于人口结构对经济增长影响的研究，主要集中于对“人口红利”以及“刘易斯拐点”的到来对经济增长的影响。人口红利概念最早是由Bloom et al（2003）[12]提出，主要是指处于工作年龄段的人口占比较高。Nayab（2008）[13]通过分析巴基斯坦人口结构特点，得出人口结构的变动主要是引起了劳动供给、储蓄以及人力资本积累三个方面改变带来的经济增长的红利。翟振武和陈卫（2007）[14]认为人口红利是人口转变过程中形成的陀螺型人口年龄结构，此人口年龄结构对经济增长起到了正向积极作用。蔡昉（2010）[15]从人口结构变动与二元经济之间存在一致性出发，阐明了人口结构与经济发展之间的内在逻辑关系，并得出我国“刘易斯拐点”将要到来的结论。史本叶（2016）[16]通过建立PVAR 模型，对我国人口结构变动对经济增长的影响进行了实证研究。得出在人口结构由红利型转向老龄化型，在此过程中将会推动经济增长方式向消费型增长方式转变。不同学者对人口红利认识稍有不同，原新和刘厚莲（2014）[17]通过辨析对人口红利的不同认识，基于劳动力资源视角得出中国的人口红利真实存在，并指出目前第一次人口红利逐渐消失，表现出逐步转向收获结构性人口红利阶段。卢飞和刘明辉（2018）[18]认为人口红利不完全等同于人口转变，其将人口红利范围扩展至人口结构、人力资本以及劳动资源的再创造三个方面，并从理论层面分析了人口红利引发的产业结构变迁，由此形成“结构效应”对经济增长的影响。

关于消费结构与经济增长的研究可追溯到马克思与恩格斯对消费资料和生产资料的部类划分。恩格尔在19 世纪末期提出的恩格尔定律才逐渐使消费结构的概念变得清晰。随着消费结构概念的提出，部分学者将其与经济增长联系起来，研究并得出其对经济增长具有重要作用[19-22]。随着专家学者研究的进一步深入，将产业结构纳入到分析消费结构对经济增长的框架当中。吴瑾（2017）[23]通过分析中国2000-2015 年城乡居民消费结构，认为消费结构升级显著诱导产业结构优化调整，从而有利于实现经济可持续增长。同样，张翠菊和张宗益（2016）[24]也得出相似结论。

由以上的研究来看，大多数研究只从产业结构、人口结构、消费结构单方面研究了对经济增长影响，虽然部分学者分析了产业结构、人口结构、消费结构两两之间关系对经济增长影响，但并未将其三者同时纳入到一个分析框架当中，而无论从理论还是现实的角度考虑，产业结构、人口结构、消费结构三者之间又存在相互影响关系，三者之间协调发展必然对经济转型发展具有重要作用。基于此，在已有文献的基础上，首先采用耦合协调度模型测算产业结构、人口结构、消费结构三系统耦合协调度（以下简称三系统耦合协调度），并分析其时空演变规律；其次，在测算三系统耦合协调度的基础上分析其对经济增长的“水平效应”“增长效应”以及“绿色效应”。

三、研究方法与测算结果分析

（一）评价指标体系的构建

构建合理的评价指标体系是研究产业结构—人口结构—消费结构三者之间关系的基础。因此，在构建评价指标体系时应遵循全面性、代表性以及科学性的原则，同时考虑到数据的可得性与可操作性，参考逯进（2018）、张凡（2017）等的做法[25-26]，围绕产业结构、人口结构、消费结构个各系统，选取17 个二级指标，进而构建产业结构—人口结构—消费结构耦合协调度发展评价指标体系，指标体系权重采用熵值法计算得出，其中关于消费结构评价指标的选择参考吴薇（2009）[27]方法将其划分生存型消费、享受型消费和发展型消费，如表1所示。

（二）耦合度及耦合协调度测算模型

耦合原是物理学中概念，表示两个或两个以上的系统之间通过各种相互作用形成了彼此之间相互影响的现象，耦合度则是用来描述各系统之间相互作用、彼此影响的程度，后来逐渐用于地理、经济等研究领域。在钱丽等（2012）、逯进和刘璐（2018）的基础上[28,25]，构建产业结构、人口结构与消费结构的耦合度及耦合协调度测算模型。

1.耦合度测算模型。物理学中耦合概念推广到多个系统的耦合度模型如下：

其中，ui是（i=1,2,3…m）各子系统评价值。由于原模型较为复杂，因此耦合度测算模型还需进一步简化。下面主要讨论n=3 时的情况，令u1、u2、u3分别为产业结构、人口结构与消费结构综合指数。因此，将（1）式子简化为（2）式：

表1 人口年龄结构—消费结构—产业结构指标评价体系及权重

其中，C 介于 0 到 1 之间 ,C 值越接近于 1 表示三者之间的关联程度越大，反之关联程度越小；当C=0时，三者则处于无关状态。

2.耦合协调度测算模型。耦合度仅仅反映了产业结构、人口结构与消费结构三个系统之间的作用强度，并不能全面反映三个系统的整体功能或协调发展水平。为此，本文将引入耦合协调度模型，其计算公式如下：

其中，T为产业结构、人口结构与消费结构综合评价值；α、β、χ为待定系数。由于人作为经济社会的主体，对消费与产业发展具有重要作用。因此，将产业结构、人口结构与消费结构子系统权 重 分 别 取 为 0.3、 0.4、 0.3。 参 考 廖 重 斌（1999）[29]关于耦合协调度分类方法，将产业结构、人口结构与消费结构三系统耦合协调度分为10个等级。如表2所示。

3.数据来源。以中国30 个省（区、市）作为研究对象（西藏数据缺失严重，因此未作为研究对象），2005年以来，我国产业结构、人口结构及居民消费结构发生了较大变动，因此，选取2005—2017 年相关数据进行具体测算。数据来源于《中国统计年鉴》《中国人口统计年鉴》《中国人口与就业统计年鉴》以及各省区市统计年鉴。对于少部分缺失数据，采用趋势拟合估算得到。

表2 耦合协调度等级划分

（三）耦合协调度的测算结果与分析

由（3）式计算得出我国各省（区、市）主要年份耦合协调度，具体计算结果见图1 和表3。从全国层面来看，我国三系统耦合协调度总体变化趋势较为平缓，但略有下降的趋势，由2005 年的0.487 下降到2017 年的0.475，出现了小幅度下降。这表明了目前我国三系统协调发展不仅处于较低水平，且表现出三系统良性互动趋势减弱，三系统协调发展面临较大压力。

分区域来看，东部地区三系统耦合协调度略高于中、西及东北部地区，并且与全国层面三系统耦合协调度变化趋势相似均呈下降态势；东北地区在2014 年之前和全国平均水平相当，而2014年之后三系统耦合协调度明显有上升趋势，且高于全国的平均水平；中、西部地区三系统耦合协调度低于全国平均水平，特别是西部地区三系统耦合协调度水平还处于全国各地区的最低水平。由此表明，我国三系统耦合协调度就目前来说还处于较低水平，不同地区之间还表现出差异性特征。

分省份来看，主要年份大多数省份的三系统耦合协调度处于濒临失调与勉强协调之间，由于不同地区经济社会发展情况不同，东部地区由于经济发展水平略好于其他地区，其三系统耦合协调度基本处于勉强协调阶段。其中，北京、天津、上海、江苏、浙江耦合协调度较高，但是均表现出下降趋势。可能的原因是以上省市均是我国经济较为发达的地区，虽然近些年来人均收入有了较大提高，但老龄化问题在这些地区也同样表现得较为突出，产业结构调整速度未能较好地适应人口结构与消费结构变化，导致了三系统耦合协调度有下降的趋势。但东部地区的海南省三系统耦合协调度有上升趋势，可能的解释是海南省立足于自身优势大力发展第三产业，优化了产业结构，提高了人均收入水平，适应了人口老龄化问题，从而促进了三系统耦合协调度的提升。中部地区的山西、安徽、河南湖北在考察期内波动上升，而江西、湖南则呈逐步下降趋势。西部地区由于经济基础较为薄弱，除贵州、云南两个省份以外其他地区三系统耦合协调度均表现出不同程度的下降。东北地区各省份2010 年之后呈现出小幅度上升趋势，这说明东北各省份在振兴东北老工业基础上，加快转变经济发展方式，优化调整产业结构，再次激活了东北地区经济发展活力，提高了居民人均收入水平，优化了消费结构，从而又进一步提高了本地区三系统之间耦合协调度水平。

图1 全国及各地区三系统耦合协调度

四、三系统协耦合调度对经济增长的实证分析

（一）模型设定

基于对三系统耦合协调度的测算，将经济增长划分为“水平效应”“增长效应”“绿色效应”三种增长形式，并具体分析三系统耦合协调对经济增长三种效应的影响。基于此，构建了三系统耦合协调对经济增长的实证模型。经济增长通常表示的是在较长的时间跨度内，一个国家人均产出（或人均收入）水平的持续增加，但当经济发展到一定程度时，不单单考虑经济增长的速度问题，更重要的是关注于经济增长质量与其是否具有可持续性的问题[30]。因此，将经济增长具体划分为“水平效应”“增长效应”以及“绿色效应”三种增长，其中三种经济增长的效应分别用人均GDP 对数、全要素生产率对数①②、绿色全要素生产率对数来衡量。由此设定如下模型：

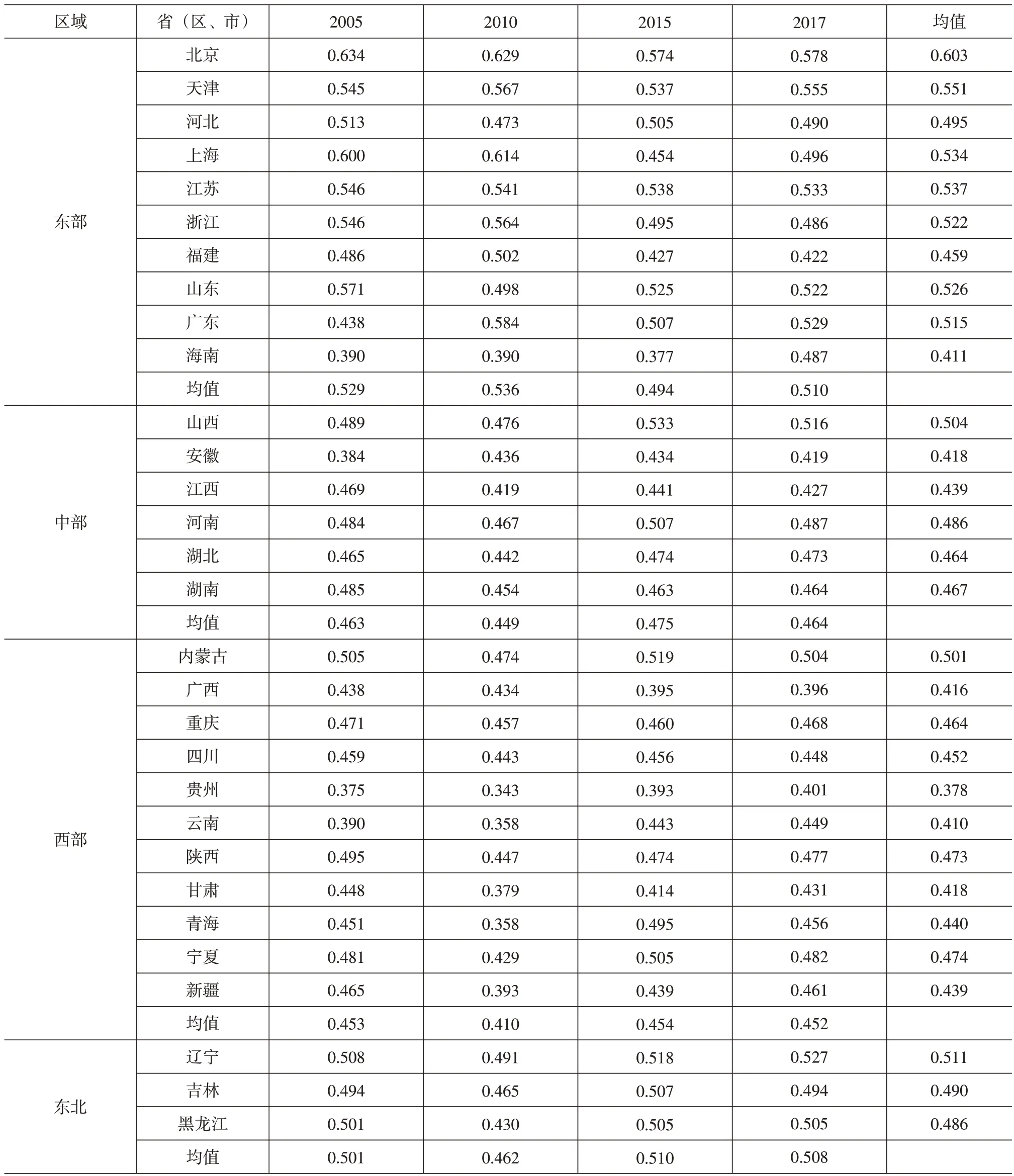
表3 各地区主要年份产业结构-人口结构-消费结构耦合协调度

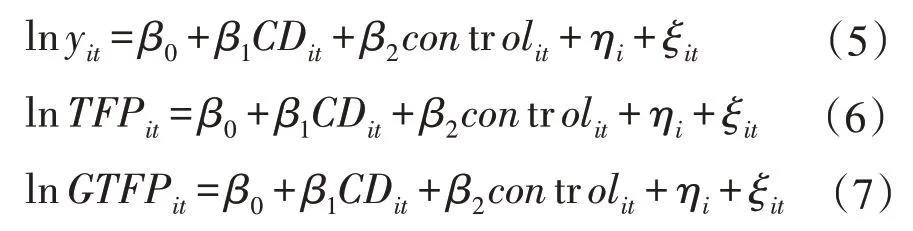
其中，i代表各省份；t为年份；η为地区固定效应；£为残差项；lny为经济增长水平效应，用人均GDP 的对数表示；TFP 为经济增长的增长效应，用Malmquist生产率指数衡量；GTFP为经济增长的绿色效应，由绿色全要素生产率表示；CD 为三系统耦合协调度；control为控制变量。

同时考虑到，首先，三系统耦合协调度本身涵盖的内容较为广泛，其与经济增长关系可能并非简单线性关系。其次，当三系统耦合协调度处于较低水平时，可能并不能有效促进经济增长，只有当其耦合协调度达到一定程度时，才能凸显对经济增长的正向作用。因此，为了验证是否三系统耦合协调对经济增长具有此类效应，在（5）-（7）式中引入三系统耦合协调度的二次项系数，最终确定为如下模型：

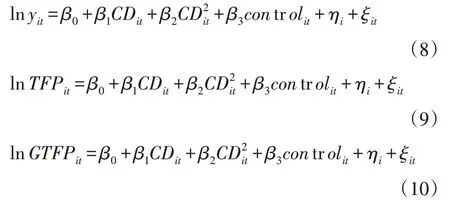
（二）变量说明

被解释变量与核心解释变量已在上文做了较为详细的说明，以下将对控制变量进行说明。

1.要素投入。要素投入作为经济增长的基础，对经济增长具有重要作用。Chow et al（2002）[37]研究认为，在1978-1998年间物质资本和劳动力投入对经济中国经济贡献率分别为62%、10%，由此得出物质资本存量和劳动力投入对经济增长的作用较为突出。本文参考Chow et al 研究将历年就业人口占总人口比重（labor）和各省份物质资本存量的对数（capital）作为要素投入指标，其中物质资本存量采用张军（2004）[38]的计算方法得到。

2.对外开放水平。对外贸易和经济增长之间的关系一直是学术界关注的热点问题，通过对外贸易和投资有助于技术改进，增强了本国的创新能力，从而促进了经济快速发展。基于此，借鉴李国璋和刘津汝（2011）[39]做法，采用各地区进出口总额占地区总值的比重（open）来衡量对外开放水平。

3.研发能力。研发能力大小在一定程度上代表了一个国家或地区创新水平的高低，对经济的增长具有重要的推动作用。其中专利的授权数（patent）表示一定时期内某地区研发能力大小（范德成（2006）[40]，因此将各地区专利授权数取对数作为衡量研发能力的标准。

4.政府规模。政府在经济增长的过程中扮演了较为重要角色，其通过纠正市场的不完全性，为市场经济的健康发展提供保障。鉴于政府对经济增长的重要作用，参考姚先国（2008）[41]做法，把地方财政支出占地区生产总值的比例（government）作为衡量政府规模的标准。

（三）实证结果与分析

1.面板数据平稳性检验与协整检验。由于有些时间序列数据并不存在直接的关联但又表现出共同的变化趋势，其数据的回归结果同样表现出较高的拟合度，但却没有任何的实际意义。因此，为了避免此类的伪回归，在面板数据模型回归之前有必要对面板数据进行平稳性检验，以确保实证结果的无偏性与有效性。采用stata13 计量软件运用相同根单位根LLC 检验面板数据的平稳性，由检验结果可看出各个变量均为水平序列平稳。检验的结果如表4所示。可知各变量通过了平稳性检验，因此进一步进行协整检验。利用Kao协整检验方法对面板数据模型中各被解释变量与解释变量进行了面板协整检验，以判断这两者之间是否存在协整关系，检验结果如表5所示。协整检验结果显示，三个被解释变量与各解释变量之间存在着长期稳定的均衡关系，因此可对模型进行回归分析。

表4 变量单位根检验

表5 面板数据模型Kao协整检验结果

2.面板数据模型回归结果分析。首先分别运用普通最小二乘法（OLS）与固定效应模型（FE）（由Hausman 检验结果显示，模型采用固定效应回归优于随机效应，因此采用固定效应模型进行回归）进行了实证回归分析，模型的计量回归结果见表6。由表6 回归结果可知，普通最小二乘法的回归结果显示三系统耦合协调对经济增长的水平效应与绿色效应的一次项系数与二次项系数均不显著，但并不能由此得出三系统对经济增长没有影响。从面板固定效应F检验的结果来看，说明面板数据固定效应模型要优于普通最小二乘法的回归，因此面板数据固定效应模型的回归结果较普通最小二乘法的回归结果准确。然后以固定效应情形为基础对模型的估计结果进行分析与解释。

由固定效应面板模型的回归结果得出，三系统耦合协调对经济增长的三种效应的影响均呈现为“U”型，由此表明三系统耦合协调对经济增长影响存在先抑制后促进的作用。具体来说，三系统耦合协调对经济增长影响存在一定的门槛效应。对于经济增长的水平效应来说，三系统耦合协调度以0.576为转折点，当耦合协调度低于0.576时，其对经济增长的水平效应具有阻碍作用，耦合协调度大于0.576时，则对经济增长的水平效应具有推动作用。同理，对于经济增长的增长效应和绿色效应来说，三系统耦合协调度的转折点分别为0.643、0.515。由此可得知经济增长的绿色效应对三系统耦合协调度门槛值较低，是因为对于经济增长的水平效应与增长效应来说其受传统生产要素影响较大，而经济增长的绿色效应则注重经济的可持续发展，一旦三系统耦合协调度水平有所提高或达到经济增长绿色效应的要求，其三系统耦合协调度将会促进经济增长绿色效应的提高，也即经济增长的绿色效应对三系统耦合协调度更为敏感。

通过上文对三系统耦合协调度的测算，得知目前虽然我国三系统耦合协调度还处于水平较低阶段，但大多数省份三系统耦合协调对经济增长的三种效应的影响还处于“U”型曲线的左边。只是对于经济增长的绿色效应来说，东部地区的部分省份以及东北地区的辽宁省三系统耦合协调度的作用由抑制转变为促进，而西部地区和中部地区大部分省份的三系统耦合协调度还未达到转折点。东部地区由于相对优越的地理条件与物质基础使其三系统耦合协调度水平整体高于全国其他地区，这也促使了该地区经济转型发展，因此其他地区也应逐渐提高三系统耦合协调度水平，以保障我国经济顺利地转型升级。

3.稳健性分析。为尽量避免内生性问题对模型估计结果的影响，运用SYS-GMM估计方法对模型进行重新估计，此方法是将解释变量的滞后项及其差分项的滞后项作为工具变量，以解决模型当中存在的内生问题（邵军和徐康宁，2011）[42]。但SYS-GMM 估计方法需要通过两项检验，其一是Arellano-Bond 检验，其二是Sargan 检验，只有通过这两项检验才能确保模型估计的有效性。通过模型估计结果来看，核心解释变量三系统耦合协调系数均未发生明显变化，表明模型估计结果具有一定的稳健性。具体估计结果如表7所示。

为进一步确保模型估计的稳健性，仍采用SYS-GMM 方法分区域对模型进行重新估计。从估计结果看，核心解释变量的符号同样也未发生明显变化，且三系统耦合协调对东部地区部分省份与东北地区辽宁省经济增长的绿色效应影响已从“U”型曲线的左边转为右边，与基准模型回归一致，由此可看出模型估计具有一定稳健性。具体估计结果如表8所示。

表6 实证回归结果

表7 实证回归结果（稳健性检验）

五、结论与政策启示

本文利用中国30 个省（区、市）的面板数据，首先，利用耦合协调度测算模型对中国30 个省区市的产业结构、人口结构与消费结构三系统耦合协调度进行测算。由测算结果可知，从总体来看，东部地区与东北地区三系统耦合协调度略高于中、西部地区，全国层面上三系统耦合协调度整体呈逐年下降态势，主要年份大多数省份的三系统耦合协调度处于濒临失调与勉强协调之间。由此表明我国三系统耦合协调度水平就目前来说处于较低水平，并且不同地区之间还表现出差异性特征。其次，在测算三系统耦合协调度的基础上，实证分析了三系统耦合协调对经济增长的三种效应的影响。具体来说，三系统耦合协调对经济增长的三种效应的影响均呈现“U”型形态，其中三系统耦合协调度对东部部分省份与东北地区的辽宁省经济增长的绿色效应的影响已从“U”型曲线的左边转变为右边，也即三系统耦合协调对其经济增长的绿色效应影响由抑制作用转变为促进作用，但由于目前我国三系统耦合协调度整体水平较低，且经济增长水平效应与增长效应受传统生产要素影响较大，三系统耦合协调度对其还未显现出促进作用。

基于研究结论，得出如下政策启示：依据对三系统耦合协调度测算结果，发现我国区域间产业结构、人口结构及消费结构之间耦合关系处于非均衡状态，并且东部地区三系统耦合协调度下降趋势较为明显。要解决区域间耦合协调度的非

均衡状态，就要根据东、中、西及东北地区各自的区位与资源优势，因地制宜，调整优化升级地区间的产业结构，促进产业结构、人口结构、消费结构协调发展，提高三系统耦合协调发展水平，最终确保我国经济可持续发展。

表8 实证回归结果（稳健性检验）

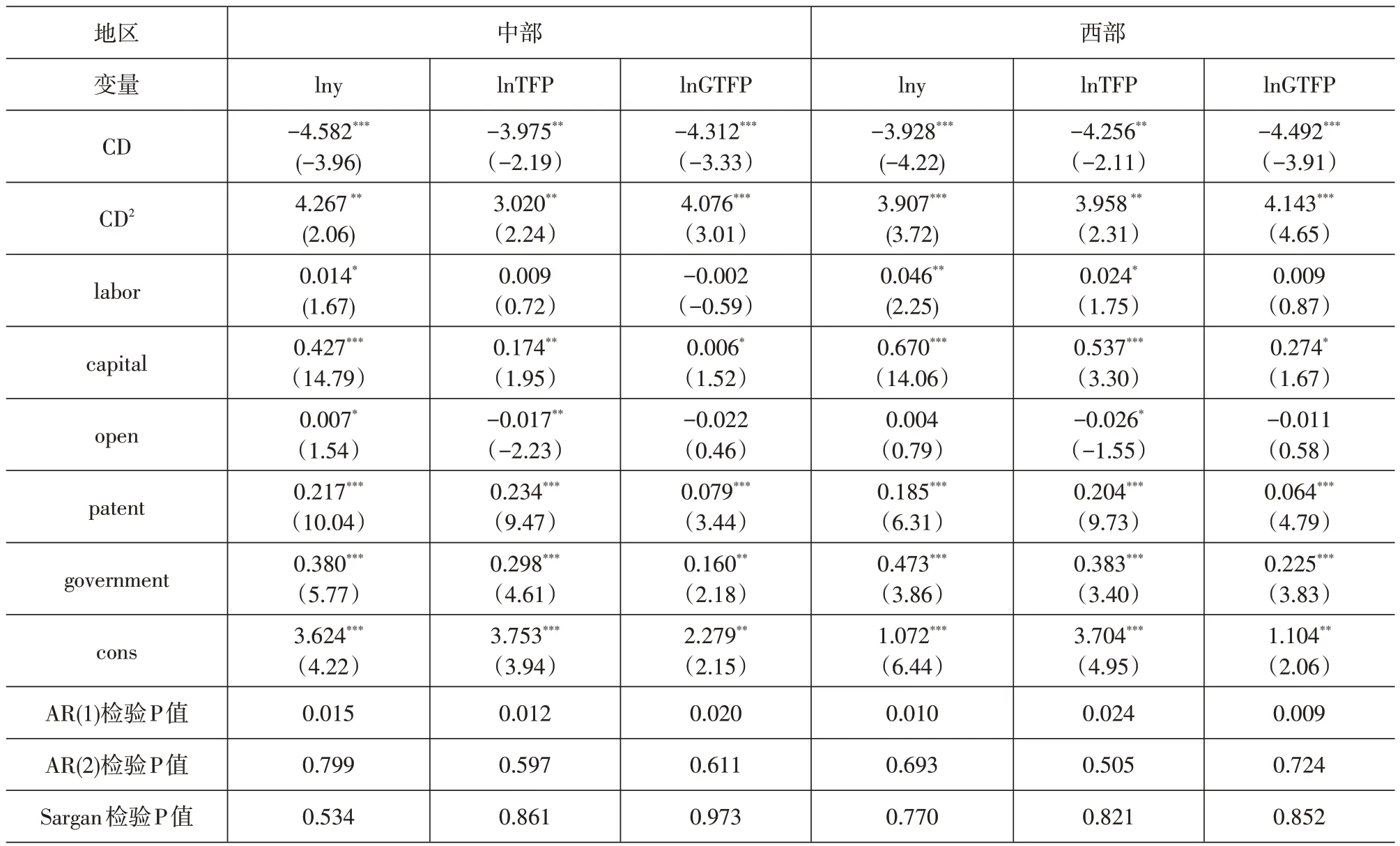
续表8

具体而言，第一，东部地区在不断优化调整产业结构的过程中逐渐优化人口结构与消费结构。东部地区产业结构、人口结构以及消费结构各自整体情况略好于其他地区，但三系统耦合协调度在近几年则表现出较为明显的下降趋势。在经济结构转型的当下，东部地区产业结构受到的冲击更大，倒逼产业结构优化升级。若只从单方面推进产业结构调整，会引起其与人口结构与消费结构之间不协调发展。因此，东部地区在推进产业结构优化升级时应充分考虑人口结构与消费结构是否与其协调发展。

第二，中部地区则要加快产业结构升级。中部地区人口结构与消费结构状态较为稳定，目前中部地区首要任务是加大承接东部地区的产业转移，按照“中国制造2025”行动计划的战略要求，大力提高产业结构水平。

第三，西部地区要精准定位，协调发展。西部地区三系统耦合协调度整体水平低于全国其他地区，说明西部地区产业结构、人口结构、消费结构三系统都急需优化调整，并且三系统之间发展又不协调。由于历史原因造成的西部地区经济发展水平低于全国其他地区，导致大量人才外流，产业结构目前仍多处于低端阶段，居民消费水平与结构长期得不到提高。因此，对于西部地区进行扶持时，要精准定位，根据地域特点发展相对应的产业，按照产业结构特征，不断优化人口结构与消费结构。

第四，东北地区则要继续提高三系统耦合协调度水平。东北地区三系统耦合协调度发展水平有略微上升趋势，因此，东北地区应进一步协调三系统之间发展，以期起到带头模范作用。

第五，提高三系统耦合协调度水平，促进经济可持续发展。经过实证研究三系统耦合协调度对我国经济增长三种效应的影响，得出三系统耦合协调度对经济增长的三种效应的影响均呈现“U”型形态，但三系统耦合协调度对东部部分省份和东北地区辽宁省经济增长的绿色效应的影响已从“U”型曲线的左边转变为右边，由此表明经济增长的绿色效应对三系统耦合协调发展变化较为敏感。但由于目前我国三系统耦合协调发展水平还处于较低水平，其他地区三系统耦合协调度对当地经济增长影响均在“U”型曲线的左边，即未对经济增长产生促进作用。因此，应加快促进三系统耦合协调水平的提高，逐渐改变经济发展方式，凸显三系统协调发展对经济增长的作用，以保障我国经济转型发展的顺利完成。

注释

注：①全要素生产率（TFP）的增长速度及其对产出增长的贡献被看作是判断经济发展方式转变和经济质量提升的主要依据[31]。然而，传统的TFP 并没有考虑经济增长所造成的环境资源损耗，因而会扭曲对经济绩效的评价，并可能在政策建议上产生误导（Hailu and Veeman， 2000）[32]。但是，从上世纪80 年代开始的地方官员之间围绕GDP 增长而进行的“晋升锦标赛”模式（周黎安，2007）[33]，不管环境资源的损耗，盲目追求GDP，即使已被“叫停”，但是其后果仍不可忽略，因此考虑传统的TFP也有很有必要的。自Chung et al.（1997）[34]在测度瑞典纸浆厂的TFP时，提出了方向性距离函数，将污染排放当作非期望产出，以测算考虑环境因素的绿色全要素生产率之后，这种方法被广泛的使用。其中，基于SBM 函数和Luenberger 生产率指数来测算绿色生产率的方法更是被大量学者使用。考虑到“温室效应”已成为全球性环境问题之一，本文参照原毅军等（2015）[35]的研究，选取CO2排放量作为非期望产出指标。

②为了考虑全要素生产率的动态变化，本文以2005 年为基期将TFP、GTFP 指数转换为累积生产率指数。考虑到部分数据为负，参考Managi和Jena（2008）[36]的做法，本文将所有值加1后再进行逐年累乘。