基于双层协同进化的多目标粒子群算法
闫 李,李国森,瞿博阳,朱小培,马佳慧
(中原工学院 电子信息学院,河南 郑州 450007)
0 引 言
实际工程中大多数优化问题属于多目标优化问题(multi-objective optimization problems,MOPs)[1]。这类问题的优化结果不是单一的,而是存在一组折衷解组成的帕累托最优解集(Pareto-optimal set,PS)[2,3]。解决这类问题的目标是获得目标空间中分布良好的帕累托前沿(Pareto front,PF)[4-6]。
在多目标问题中,一些优化问题具有多模态的特性。如路径规划问题[7]、背包问题[8]、车间调度问题[9],这类问题属于多模态多目标优化问题(multimodal multi-objective optimization problems,MMOPs)[10],其特点是决策空间中的多个PS映射到目标空间中相同的PF。解决这类问题的目标是获得决策空间中多个帕累托解集。
对此国内外许多学者提出算法以解决多模态多目标优化问题。Liu等[11]利用双保存集与重组策略提高解集在目标与决策空间中的多样性和收敛性。Xu[12]采用变异边界处理方法以提高种群多样性,并采用个体预选择机制提高搜索精度。Ishibashi[13]使用决策空间中分布良好的个体优化每个子问题,以保持决策空间中个体的多样性。
上述研究在解决多模态多目标问题上做出了很多工作,但仍然存在获得的帕累托解集不完整、算法收敛性较差等不足。本文以多目标粒子群算法(multi-objective particle swarm optimization algorithm,MOPSO)[14-16]为框架,提出基于双层协同进化的多目标粒子群算法(DCMOPSO)。算法采用双层协同进化机制以定位更多的解,利用决策空间拥挤距离以保持解的多样性。最后,通过对比实验验证DCMOPSO算法的性能。
1 基本概念
1.1 多模态多目标优化问题
如图1所示,决策空间中的PS1、PS2对应目标空间同一个PF[7]。决策空间中A1和A2分别位于PS1、PS2,但在目标空间中都对应同一点A′。同时求出可行方案A1和A2,这给决策者选择合适的方案提供了很大的灵活性[17]。

图1 多模态多目标优化问题
1.2 粒子群算法描述
设一个由NP个粒子组成的种群在M维决策空间中进行寻优。在t时刻,第i个粒子从当前位置xi(t) 以速度vi(t) 朝着其个体历史最优pbesti(t) 和全局最优nbesti(t) 的方向飞行[18]。则在 (t+1) 时刻,该粒子的速度vi(t+1) 和位置xi(t+1) 分别定义为
vi(t+1)=wvi(t)+c1r1(pbesti(t)-xi(t))+
c2r2(nbesti(t)-xi(t))
(1)
xi(t+1)=xi(t)+vi(t+1)
(2)
其中,w为惯性权重,c1和c2为加速系数,r1和r2为[0,1]之间的随机值。
2 基于双层协同进化的多目标粒子群算法
2.1 双层协同进化机制
在传统粒子群算法中,粒子间几乎没有信息交流,且采用全局最优解更新各个粒子的位置,这将导致许多粒子过早收敛而降低了全局寻优能力和种群多样性,因此很难在决策空间找到多个解。另外,在连续多目标优化问题中,其真实帕累托解集在决策空间中是一个分段连续流形。如果使种群中的粒子逐渐飞向这些帕累托解集周围,那么将能够获得大量的帕累托解集。
基于此,本文提出双层协同进化机制,该机制采用上下两层,并将整个种群均分成两个子种群,即上层一个探测种群和下层一个跟随种群。探测种群采用外部档案EXA中的精英解以引导进化,尽可能逼近帕累托解集,并较均匀地分布在帕累托解集的周围。跟随种群负责跟随探测种群,并学习探测种群的历史最优信息,加强局部的开采能力。具体方法为:

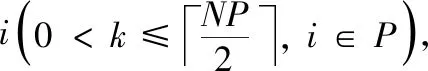
然后探测种群、跟随种群协同进化。其基本思想是探测种群中每个粒子采用全局最优引导以收敛到全局最优,而跟随种群中的每个粒子跟随其伙伴的个体历史最优以增强开采能力。对于探测种群中第i个粒子 (i∈P),其速度更新公式如下
vi(t+1)=wvi(t)+c1r1(EXA(k)-xi(t))
(3)
对于跟随种群中第j个粒子 (j∈Q),其速度更新公式如下
vj(t+1)=wvj(t)+c1r1(pi(t)-xj(t))
(4)
双层协同进化机制如图2所示。整个种群划分为探测种群和跟随种群。跟随种群中的粒子跟随其在探测种群的伙伴,且不受其它粒子的影响,进而形成若干个邻域以提高种群的多样性。而探测种群中的不同粒子跟随不同的全局最优nbest。探测种群中的粒子不断改善其位置,并将历史最优信息反馈给跟随种群,以协同进化定位更多的解。

图2 双层协同进化机制
2.2 决策空间拥挤距离
在多模态多目标问题中,相距很远的多个解可能对应目标空间中同一点,导致在目标空间中这些解的拥挤距离会很小。如果只考虑解在目标空间的分布情况,这些解在选择过程中会被删除,即很难保留决策空间中的拥挤距离大的解。
因此本文引入基于决策空间的拥挤距离度量,以提高最优解在决策空间的分布性。具体计算方法:首先将所有个体按照快速非支配排序的方法进行分层。然后根据每个决策变量对该层所有个体按升序进行排序以便计算每一层中的每个个体的拥挤距离。设决策变量维数为M,个体数为N,Ind(i).distance为第i个个体 (1≤i≤N) 在第m个变量 (1≤m≤M) 上的拥挤距离,Ind(i).m为个体i在第m个变量上的值。对于非边界点个体,拥挤距离计算如下

(5)
其中,Indmin.m、Indmax.m分别为该层所有个体在第m个变量上的最小值和最大值。对于边界点个体,拥挤距离计算如下
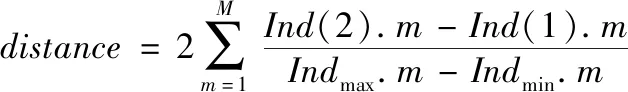
(6)

(7)
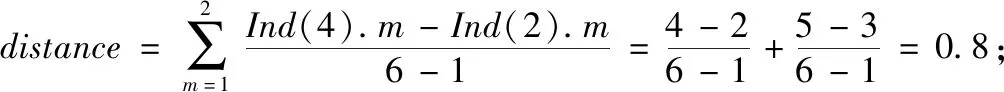

图3 决策空间拥挤距离
2.3 算法具体流程
步骤1 设置算法的种群大小NP、学习因子(c1)、最大迭代次数MaxIter,初始化种群POP,外部档案EXA=POP。
步骤2 根据双层协同进化机制划分探测种群、跟随种群。
步骤3 根据双层协同进化机制为探测种群中的粒子分配nbest。
步骤4 探测种群中的粒子根据式(3)进行速度位置更新,跟随种群中的粒子根据式(4)进行速度位置更新。
步骤5 更新外部档案EXA=[POP;EXA],对外部档案进行非支配排序以及决策空间拥挤距离的计算,选择前NP个解存入EXA。
步骤6 若迭代次数达到最大迭代次数MaxIter,输出外部档案EXA,否则,返回步骤3。
2.4 算法复杂度分析
DCMOPSO算法的主要运算是划分上下层种群,分配最优领导nbest和计算拥挤距离。假设NP表示种群以及外部存档的规模,M表示决策变量的个数,N表示目标函数的个数。划分上下层种群和分配最优领导nbest都需要计算每个个体与其它个体的距离,故其计算复杂度均为O(NP2)。拥挤距离的计算需要先判断支配关系,其计算复杂度为O(M*NP2)。计算拥挤距离的复杂度为O(M*NP*logNP)。因此,整个DCMOPSO算法的计算复杂度为O(M*NP2)。而基本的MOPSO算法的计算复杂度为O(N*NP2)[19],因此在计算复杂度上,当决策变量的个数M和目标函数的个数N相同时,DCMOPSO算法和基本MOPSO算法具有同样的计算复杂度。
3 实验和分析
3.1 测试函数
本文采用12个经典的多模态多目标测试函数[20],包括MMF1-MMF8[7]、Omni-test[12]、SYM-PART simple[21]、SYM-PART rot.+trans.[21]以及SYM-PART rotate[21]。
3.2 实验设置
本文将提出的DCMOPSO算法与6种多目标算法进行比较,包括MO_Ring_PSO_SCD[7]、DN-NSGAII[11]、Omni-optimizer[12]、NSGA-II[4]、MOEA/D[5]、PESA-II[6]。其中,DCMOPSO算法参数如下:c1=2.05,w=0.7298。其它算法的参数设置与相应文献保持相同。各算法的种群规模NP和最大迭代次数MaxIter分别为800和100[7],外部档案大小为800。每个算法在12个测试函数上独立运行25 次,结果取平均值。采用Matlab R2014b进行仿真,运行环境为Windows 7 操作系统,Intel(R) Core(TM) I7-4790 处理器,16 GB内存。
3.3 评价指标
本文采用帕累托解集近似性(PSP)[7]和超体积(Hv)[22,23]两种指标对比不同算法的性能。PSP用于评价算法所获得PS的收敛性和多样性。Hv主要反映算法所获得PF的收敛性和多样性[24]。PSP值越大说明获得的PS在决策空间中更逼近真实的PS,且具有良好的分布性。Hv值越大说明获得的PF在目标空间中更具有多样性且接近真实的PF。
3.4 实验结果
3.4.1 各策略性能对比实验
为了验证所提策略的有效性,将DCMOPSO算法和MOPSO(基本的多目标粒子群算法)[7]、DCMOPSO-I(仅采用双层协同进化机制的MOPSO算法)和DCMOPSO-II(仅采用决策空间拥挤距离的MOPSO算法)进行比较。在不同策略下算法PSP的均值、标准差和秩和检验的h值见表1。

表1 各策略PSP指标统计
从表1可以看出,DCMOPSO-I的性能优于MOPSO,DCMOPSO-II的性能略优于MOPSO。因此,采用双层协同进化机制和决策空间拥挤距离度量能够改善基本MOPSO算法的性能。此外,秩和检验的结果进一步表明,DCMOPSO 结合这两种策略能够显著提升算法的性能。其原因在于双层协同进化机制使DCMOPSO算法能够找到更多的最优解。双层协同进化机制在决策空间中将种群划分探测种群、跟随种群,并选择外部存档中的最优解为上层探测种群分配nbest,使探测种群不断逼近真实帕累托解集;跟随种群中的粒子不断跟随探测种群中其对应的伙伴粒子,进而形成若干邻域,并在其邻域内进化,以维持种群的多样性。采用决策空间拥挤距离度量以评估解在决策空间的拥挤度,使得拥挤度小的解优先被保留,而拥挤度大的解由于多样性很差而优先考虑被剔除,提高了解在决策空间的分布性。
综上所述,双层协同进化机制和基于决策空间的拥挤距离度量能够提高算法的性能。
3.4.2 不同算法的性能对比实验
本节将提出的DCMOPSO 算法与6种多目标算法进行比较。首先,比较所有算法在决策空间中获得PS的能力。所有算法的PSP指标值见表2,可以看出DCMOPSO在所有测试函数上显示出较好的性能,明显优于其它6种算法。MO_Ring_PSO_SCD的表现次之。MO_Ring_PSO_SCD采用环形拓扑以形成多个小生境,有助于找到更多最优解。DN-NSGAII和Omni-optimizer的表现相似。DN-NSGAII和Omni-optimizer均考虑解在决策空间的拥挤度,这提高了算法的性能。NSGA-II、MOEA/D和PESA-II表现较差,原因在于这3个算法没有考虑解在决策空间中的分布,不能保留决策空间中多样性好的解。其次,评价所有算法在目标空间中获得的PF的性能。所有算法的Hv指标值见表3,可以得出结论DCMOPSO算法在Hv性能指标上的表现不是最好的。但是,所有算法在同一测试函数上的Hv指标值彼此很接近。原因是所有算法均考虑了最优解在目标空间中的分布。

表2 不同算法PSP指标统计

表3 不同算法Hv指标统计
图4给出了SYM-PART rot.+trans的真实PS和PF,该函数具有9个PS。为了直观比较算法性能,图5和图6分别给出了所有算法在测试函数SYM-PART rot.+trans上得到的PS和PF。从图5可以看出,DCMOPSO能够找到9个PS。MO_Ring_PSO_SCD、DN-NSGAII和Omni-optimizer 找到的PS并不完整,且有缺失。NSGA-II、MOEA/D和PESA-II获得的PS更少。从图6可以看出,所有算法在SYM-PART rot.+ trans测试函数上都能够获得较好分布的PF,且差别不大。

图4 SYM-PART rot.+trans的真实PS和PF

图5 各算法所获得的PS对比

图6 各算法所获得的PF对比
综上所述,和其它算法相比,DCMOPSO在决策空间中表现出更好的性能,且能够获得更多的PS。
3.4.3 算法的收敛性比较
为了比较算法的收敛性[7],将4个多目标算法(DCMOPSO、MO_Ring_PSO_SCD、Omni-optimizer、DN-NSGAII)进行比较。NSGA-II、MOEA/D和PESA-II在决策空间的性能很差(见表3),故不再进行比较。本次实验选择在测试函数MMF4上进行测试。MMF4是由4段曲线(PS)组成的PSs,每段曲线对应同一个PF。如图7所示,将决策空间划分为4个区域,分别为区域1、区域2、区域3 和区域4。因此每个区域面积相等,且均有一个PS。算法的收敛性是指每次迭代种群分布在每个区域中解的比例[7]。理论上,如果算法在测试函数MMF4上具有良好的收敛性能,那么每个区域中解的比例应等于0.25。

图7 测试函数MMF4的PSs分布
图8展示了算法在100次迭代过程中每个区域中解的比例变化曲线。从图8(a)中可以看出,区域1、区域2中解的比例随迭代次数增加而先上升后下降,而区域3、区域4所在的曲线呈先下降后上升趋势。在迭代次数趋近于60时,4个区域解的比例基本上接近0.25。这反映了DCMOPSO算法的收敛性能良好。对于MO_Ring_PSO_SCD的收敛性(如图8(b)所示),每个区域解的比例最终能够稳定在0.25左右。但是区域1、区域2的解的比例略大于区域3、区域4的解的比例。这说明MO_Ring_PSO_SCD的收敛性略差于DCMOPSO。对于DN-NSGAII的收敛性(如图8(c)所示),在第30次迭代以后,区域1、区域4的解的比例低于区域2、区域3的解的比例,且未收敛到0.25。这说明更多的种群个体聚集到了区域2、区域3。对于Omni-optimizer的收敛性(如图8(d)所示),在第45次迭代以后,区域1、区域4的解的比例高于区域2、区域3 的解的比例,且不接近0.25。这意味着大多数的种群个体收敛到了区域1、区域4。同时,在图8(c)、图8(d)中,每个区域解的比例变化频繁震荡,且不稳定。因此DN-NSGAII、Omni-optimizer算法的收敛性能很差。综上所述,DCMOPSO算法具有更好的收敛性能。

图8 各算法的收敛性对比
4 结束语
本文提出了一种基于双层协同进化的多目标粒子群算法(DCMOPSO)。该算法采用了双层协同进化机制和决策空间拥挤距离度量。双层协同进化机制采用上层探测种群不断地逼近帕累托解集,下层跟随种群不断地跟随其探测种群中的伙伴粒子。决策空间拥挤距离度量用于评估粒子在决策空间的拥挤度来维持帕累托解集在决策空间的多样性。通过和6个多目标算法进行比较,验证了DCMOPSO算法能够获得更多的帕累托解,且在决策空间具有很好的收敛性。下一步工作将应用DCMOPSO算法解决实际工程问题。

