A split target detection and tracking algorithm for ballistic missile tracking during the re-entry phase
Muhmm As , Sumir Khn , Ihsnullh , Zhi Mehmoo , Yifng Shi ,Sufyn Ali Memon , Uzir Khn ,*
a Department of Electrical and Computer Engineering, COMSATS University Islamabad, Abbottabad Campus, Pakistan
b Department of Computer Science, COMSATS University Islamabad, Abbottabad Campus, Pakistan
c Electrical Engineering Department, Indus University, Karachi, Pakistan
d Department of Automation, Hangzhou Dianzi University, Xiasha Higher Education Zone, 2nd Street, Hangzhou, 310018, China
Keywords:Split event probability JIPDA Data association Ballistic missile Estimation
A B S T R A C T In the re-entry phase of a ballistic missile, decoys can be deployed as a mean to overburden enemy defenses.This results in a single track being split into multiple track-lets.Tracking of these track-lets is a critical task as any miss in the tracking procedure can become a cause of a major threat. The tracking process becomes more complicated in the presence of clutter.The low detection rate is one of the factors that may contribute to increasing the difficulty level in terms of tracking in the cluttered environment.This work introduces a new algorithm for the split event detection and target tracking under the framework of the joint integrated probabilistic data association (JIPDA) algorithm. The proposed algorithm is termed as split event-JIPDA (SE-JIPDA). This work establishes the mathematical foundation for the split target detection and tracking mechanism. The performance analysis is made under different simulation conditions to provide a clear insight into the merits of the proposed algorithm. The performance parameters in these simulations are the root mean square error(RMSE),confirmed true track rate(CTTR) and confirmed split true track rate (CSTTR).
1. Introduction
Split target tracking is a sub-field of multi-object tracking where one object or track splits into more than one child tracks.Birth of a new track transforms the single object tracking problem to a multiobject tracking problem. Defense system has many applications related to the split target tracking such as ballistic missile tracking,which is discussed in this work as one of the applications of the split target tracking problem.
Short-range and medium-range ballistic missiles can be easily intercepted in the re-entry phase. However, in the re-entry phase,decoys may be deployed,which in turn may be detected as multiple objects for the radar.The tracker has to be intelligent so as to track each object (both decoy and the real target) in the presence of clutter as any object can carry a potential threat.It is a challenging task for the tracking system to track a ballistic missile in the reentry phase because of limited time for the object tracking,sensor noise, and less a priori information about the target. The state of the ballistic missile such as position, velocity, and ballistic coefficients are estimated through different filters [1,2]. Performance parameters for these filters are accurate in terms of estimation and processing time.
The probabilistic data association (PDA) [3-5] is the Bayesian solution for the problems related to the single-scan data association.The PDA algorithm works well for the cases when there is only a single target to be tracked but PDA algorithm does not provide any framework for false track discrimination. The false track discrimination problem is solved in the integrated probabilistic data association algorithm (IPDA) [6-8] along with the target trajectory state update.
Two-step multiple hypothesis trackers (MHT) [9-11] which is itself a multi-scan target tracking algorithm is used to achieve the accuracy in tracking of the target [12]. [13] proposed a target tracking algorithm in a densely cluttered environment using multiscan data association approach by considering the target existence as an event. The high clutter density performance of the MHT algorithm is improved by combining it with the modified logic-based track initiation method.It is used in high clutter density for the split and merge issues along with the measurement noise and missdetection cases [14].
In a multi-target tracking system,the problem of measurement to track association is rectified by in-cooperating the joint association events into target tracking [15]. Multi-target tracking algorithms are compared for the single-scan and multi-scan data association problem [16]. The JIPDA algorithm is used to track the multi-target scenario in Ref.[17],but the track split scenario is not considered as an event and the target is tracked by conditioning on only birth and death events.The multiple target tracking problem is also addressed in Ref. [18], where authors have assumed the extended target scenario. In Ref. [19], authors have reduced the computational complexity of multi-target tracking algorithm by utilizing the Markov chain for random data associations.
The target tracking problem is divided into different events such as a birth event, death event, merge event and split event for the target. To improve the target tracking performance and completeness,its state should be updated by conditioning over all the events.The earlier tracking algorithms assumed only birth, death and merge events, but the split is only considered as a birth of a new track.In Ref.[20],split target tracking is accomplished by using the IMM-JPDA algorithm. This algorithm provides no mathematical formula for split detection and confirmation. No track quality measure is provided in the same algorithm [21]. also utilizes the IMMJPDA algorithm to track the missiles (ballistic and intercontinental) in maneuvering and to detect the decoys [22]. uses the IMM-like algorithm for split target tracking in a clutter-less environment. Thus no data association and track quality measures are provided, at the same time this algorithm has not presented any framework for split event detection and confirmation.
In the proposed work a new split event detection and tracking mechanism is integrated with the JIPDA algorithm and is termed as split event JIPDA (SE-JIPDA). In the best knowledge of authors, no significant mathematical contribution is made in the literature to track the split targets by considering the split as an event. The major contributions of the proposed work are:
●A novel mathematical framework is proposed for split event detection and confirmation.
●Tracking and management of track-lets.
●Integration of split event detection/tracking algorithm with the existing JIPDA algorithm.
●Performance validation of the proposed algorithm in the cluttered environment.
In Section 2 mathematical modeling of SE-JIPDA is presented,Section 3 provides simulation and analysis of results,and in Section 4 the proposed work is concluded.
2. Mathematical model
Ballistic missile has three phases; boost phase, mid-course phase and the re-entry phase as shown in Fig. 1. Anti-ballistic missile defense system mostly works in the re-entry phase. Ballistic missile deploys the decoys in the re-entry phase,this employs that a single target splits into multiple targets.In this work,a split event joint integrated probabilistic data association (SE-JIPDA) is developed for proper detection of split event and tracking of these split tracks in the cluttered environment.
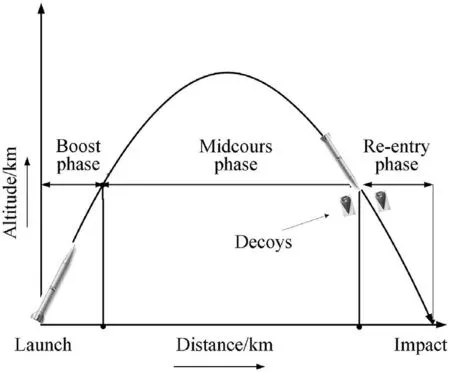
Fig.1. Ballistic missile trajectory with three phases.
2.1. Target measurement and motion model
In this study,the model under consideration is constant velocity model. The trajectory state xkis equal to

where x and y are position coordinates,andandare velocities in both x and y coordinates, respectively. Target trajectory state propagates as


02is second order zero matrix andis second order identity matrix. T is the sample time. The object measurement model is

where H is measurement matrix, and vkis white Gaussian measurement noise.

2.2. Tracking process
2.2.1. Track initialization
Tracks in each scan are initialized using two point differencing method.

2.2.2. Measurement selection
The criteria in(8)is applied to every ithmeasurement from the measurement set ykto identify the selected measurements in the validation gate.

Sτis the measurement innovation covariance matrix calculated by standard Kalman filter.is predicted position of the target.g is the gating threshold, and its value is selected as 13.3 due to 3σ limit on the standard deviation.
2.2.3. Measurement likelihood
The measurement likelihood for the ithmeasurement yk(i) in the measurement vector ykgiven target existence[8]is calculated as
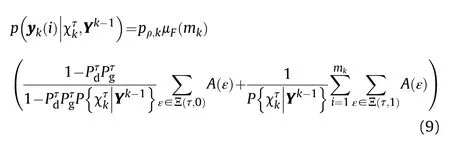
and ρkis clutter density.is the ithmeasurement likelihood in event ε with respect to the target η under normal distribution.
Of what colours are they? If that s all, said the first tailor, they are most likely black and white, like the kind of cloth we call pepper-and-salt
2.2.4. Data association
The data association probabilityfor each ithmeasurement is computed by using the formulation provided in Refs.[8,16].is used for each ithmeasurement as its weight associated with the track.is defined as

For i>0,

where

For i = 0,

and

2.3. Tracking update process
2.3.1. Target existence state update
The target existence state is updated as [16].

2.3.2. Target trajectory state update
Each measurement is used to update the target trajectory state using prior trajectory state and its predicted error covariance matrix.

2.4. Split tracking algorithm
The split tracking algorithm contains the following stages.
2.4.1. Split track initialization
At scan k,the validation gate is formed using a predicted state of parent track tparent.There should be more than one measurements inside the validation gate to start the split track initialization procedure as shown in Fig. 2 (for a special case of a single split). A cluster of measurements is formed at any scan k.Cluster formation mechanism and conditions are summarized below.
a) Number of clusters depend on the choice on number of possible splits.Its a good exercise to consider every measurement in the validation gate to be a candidate of a possible split track.Here,in this study, two splits are considered.
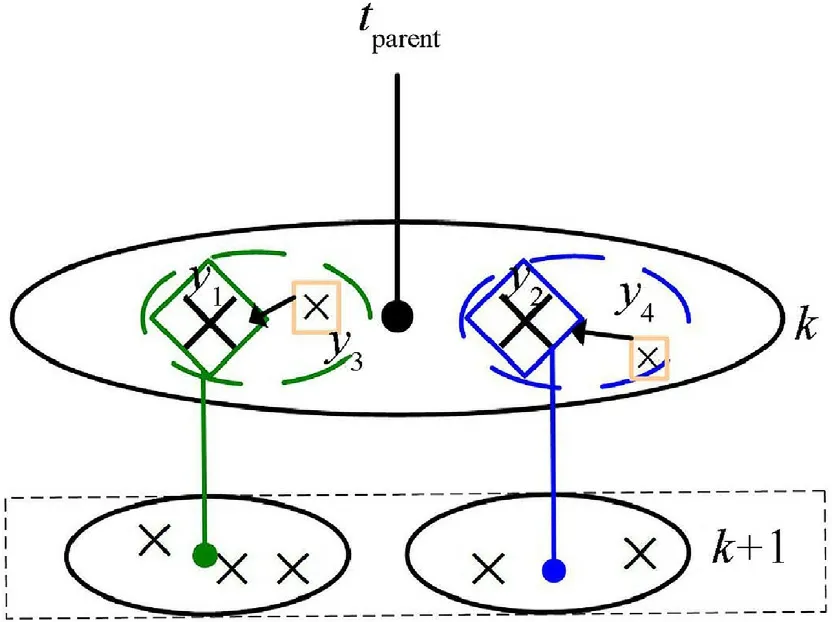
Fig. 2. Initialization pattern of tentative split tracks.
b) If their are more number of measurements than the number of possible split tracks (as depicted in Fig. 2), then the data association is calculated for each ithmeasurement in the validation gate as

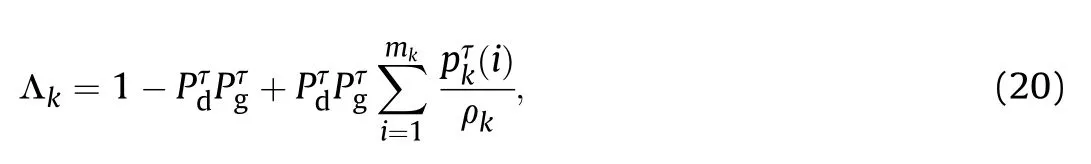
where mkdefines the number of measurements in the validation gate. The measurements with highest probabilityassociated with the predicted position of parent track tparentare used to define the center of each cluster. Each cluster becomes a source of tentative split track.In Fig.2,the measurements[y1,y2]have higher data association probabilities (19) as compared to [y3, y4]. Thus the former set of measurements are selected as a center of each cluster.
c). If their are more number of measurement than the number of possible split tracks, then these measurements are associated with either cluster based upon their normalized distance square measure with respective clusters.
By following the identical procedure more clusters can also be formed.In this work for the sake of simplicity,only two clusters are assumed to be formed. Whenever, tentative split tracks share measurements, joint integrated probabilistic data association(JIPDA) algorithm is used for measurement to track association. In this particular scenario,it becomes a multi-target tracking problem.
2.5. Data association probability of each selected measurement is calculated as

sI is index of split track and i is index of measurement.
Measurement likelihood of the ithmeasurement in the validation gate is equal to

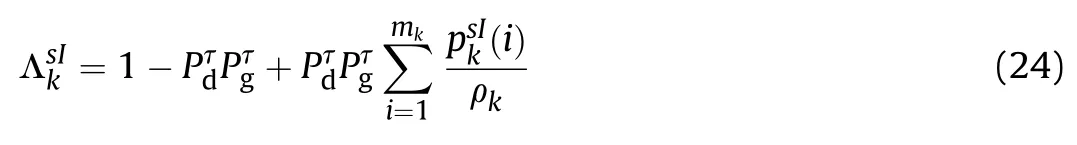
and

where
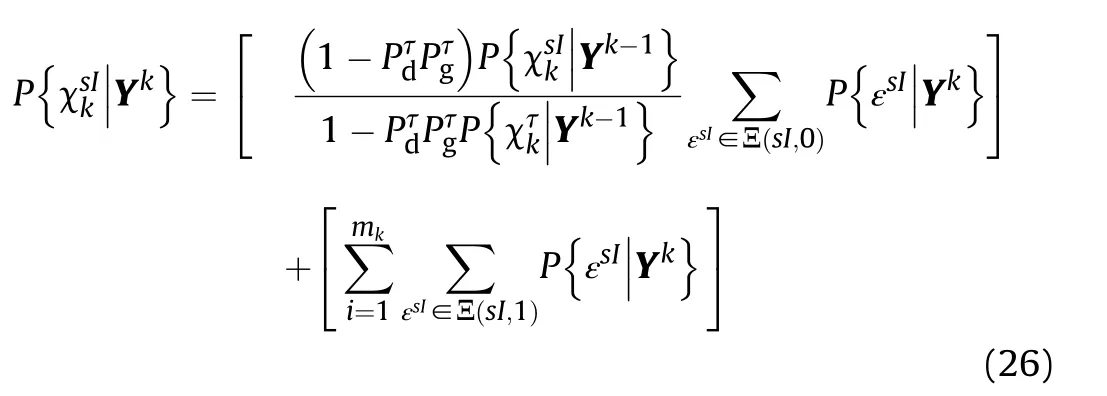
and the joint event probability is updated using

Each cluster becomes a tentative split track. The measurement in each cluster is used to update the tentative split track trajectory stateand its error covariance matrix



2.5.1. Split event probability
The split event probability is conditioned on the target existence event such that the target exists and it splits into more(in this case two) targets. A situation may arise such that, target exists and it does not split with probabilityThe event that target exists and splits and the event that target exists and does not split are mutually exclusive and exhaustive events.

and

The split event probabilityof the sIthtrack after tentative split eventis computed as,
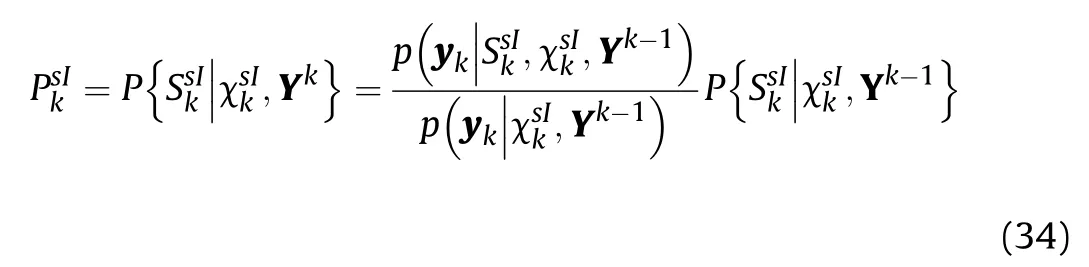
where

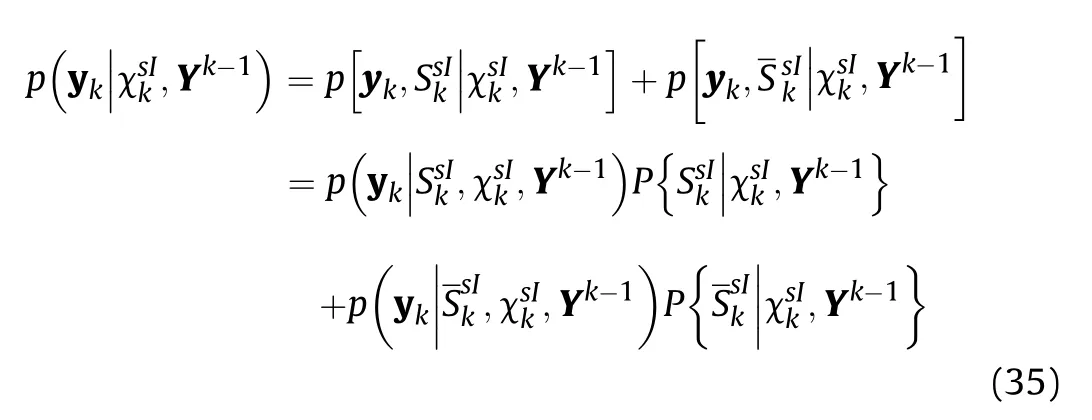
As the non split track is equivalent to its non existence. Thus
As,sIthsplit track event is directly related to its respective event of existence, thus (36) becomes
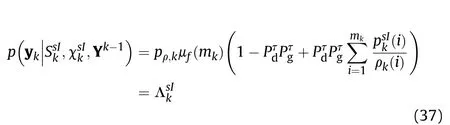
The non-split event collapse into the non-existence event,thus

2.6. The measurement likelihood in (35) becomes

Thus (34) becomes

2.6.1. Confirmation of split track
All the tentative split tracks are checked for the status of split track confirmation. There are two conditions for the split track confirmation.
i) Condition on separation distance.
ii) Condition on split confirmation probability threshold. Both conditions (41) and (42) should be satisfied at once by the tentative split track to get the status of confirmed split track.
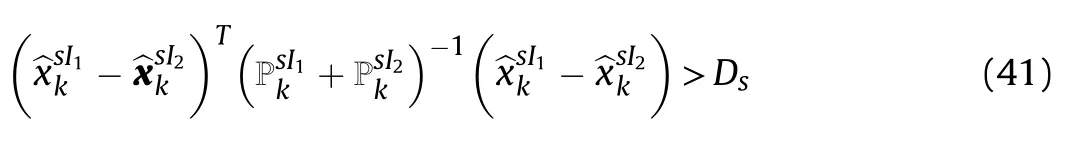
and

where Dsis separation distance in meters between the two tentative split tracks.For this particular scenario,it is selected as 20 mis the split confirmation threshold and is selected as 0.95.sI1and sI2are the indexes of any two tentative split tracks under consideration.is the split track trajectory estimate and its error covariance matrix calculated using standard JIPDA algorithm(whenever tracks share some measurements).
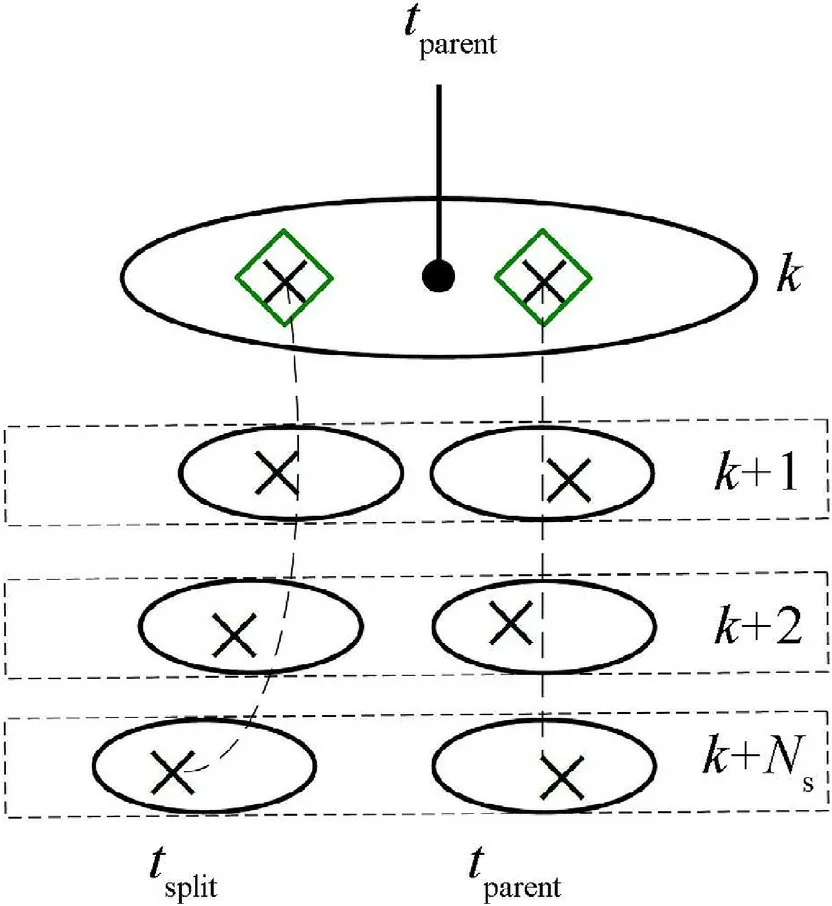
Fig. 3. Progress of confirmed split tracks.
The confirm split tracks propagation scenario is presented in Fig.3.In the initial scans,track-lets are identified as tentative split tracks.If both the conditions in Eqs.(41)and(42)are satisfied,then tentative split tracks attains the status of confirmed split track in scan k+Ns.Where Nsis the number of additional scans used for the split track confirmation.
2.6.2. Merger of tentative split tracks
If the tentative split tracks persist to follow the same path in parallel for“Nm”scans,then these tracks will be merged as they will only increase the computational complexity.

Fig. 4. Parallel progress of two tentative split tracks.

Table 1 Algorithm for SE-JIPDA
The process is depicted in Fig. 4. In this particular case if the tentative split tracks satisfy the check (43) for “Nm” consecutive scans, then the tentative split tracks are merged to create a single track.

where Dmis the merging threshold between the tentative split tracks.In this study,″Nm″is selected as 7 scans,and Dsis selected as 5 m.Pseudo code for split event JIPDA(SE-JIPDA)is given in Table 1,which shows the overall flow of the split event detection and tracking mechanism as discussed in the previous sections.
3. Simulation study
Ballistic missile trajectory is shown in Fig. 5. Results are presented for two different cases.

Fig. 5. Ballistic missile trajectory with decoys.
In Case-1, target and its decoy are far from each other as compared to Case-2,where the target and its decoy is close to each other. Both cases are presented in Fig. 5. Initial position of the parent target is[100 m;1290 m].At scan 29,the parent target splits into two track-lets creating a multi-target scenario in the surveillance area. Each track-let is considered as a target to be tracked in the presence of clutter.In Case-1,the velocities are[2500;-500]m/s and [2400;-700] m/s for parent target and split target, respectively. In Case-2, the velocities are [2500;-500] m/s and [2400;-600] m/s for parent target and split target, respectively. The surveillance area under observation is [3000 m × 800 m].
In each case, the comparison is made for different values of detection probability Pd(for clarity in the figures,is replaced by Pd),while keeping the same clutter density.Simulations are carried out in MATLAB with a total of 100 Monte Carlo runs with each Monte Carlo run having 50 scans.
3.1. Case-1 analysis

Fig. 6. Case-1:Cumulative RMSE for both parent and split tracks ρ = 10-6m-2,Pd =1,0.85,0.7.
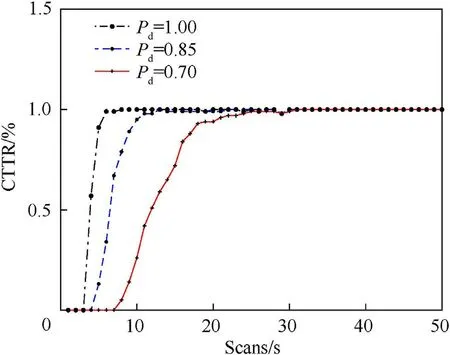
Fig. 7. Case-1:Confirmed true track rate (CTTR) of parent track ρ = 10-6m-2,Pd =1,0.85,0.7.

Fig.8. Case-1:Confirmed split true track rate(CSTTR)of split track ρ =10-6m-2,Pd =1,0.85,0.7.
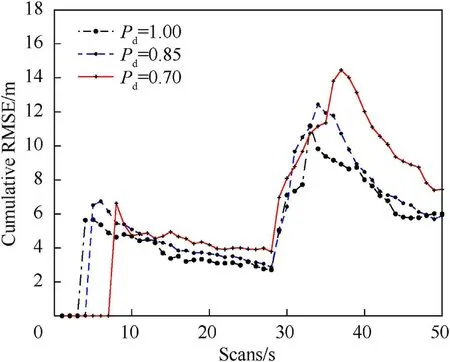
Fig. 9. Case-2: Cumulative RMSE for both parent and split tracks ρ = 10-6m-2,Pd =1,0.85,0.7.
Simulation results in Case-1 are compared for different values of Pd(1,0.85,0.7)by keeping the same clutter density(ρ =10-6m-2).With the low probability of detection,the RMSE increases as shown in Fig. 6. The RMSE plot is cumulative for both parent and split track.In the splitting phase,the RMSE increases due to the fact that both parent track and split track RMSE’s are added up.Fig.7 shows the confirmed true track rate for the parent track.A small variation can be observed in the scan interval 27 to 30, when parent target shares the measurements with the split target.
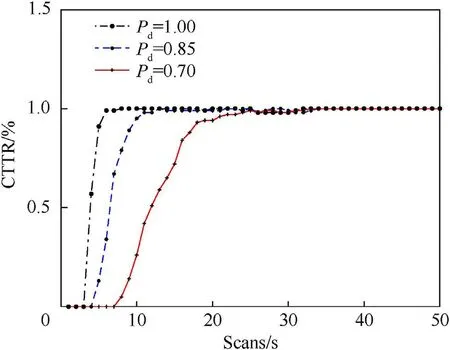
Fig.10. Case-2: Confirmed true track rate (CTTR) of parent track ρ = 10-6m-2,Pd =1,0.85,0.7.

Fig.11. Case-2:Confirmed split true track rate(CSTTR)of split track ρ =10-6m-2,Pd =1,0.85,0.7.
Confirmed split true track rate(CSTTR)characteristic is analyzed for the Case-1 for different values of Pdas shown in Fig. 8. It is a unique performance parameter of the proposed algorithm, as it helps in the analysis of split detection and its tracking.In Fig.8,the CSTTR starts to increase showing the presence of split and attains the maximum value till the end of the complete run.
3.2. Case-2 analysis
In Case-2, both target and decoy are close to each other. In this particular case, multiple tracks share measurements for a greater number of scans as compared to Case-1. In Figs. 9-10, there is comparison of RMSE and CTTR for ρ = 10-6m-2. It is visible that RMSE increases and CTTR slow down with a decrease in the value of Pd. Fig.11 shows the CSTTR for the Case-2.
3.3. Comparison of Case-1 and Case-2
The CTTR performance for both cases is identical as the same clutter density and target motion model is considered. Due to the large separation in Case-1, targets share measurement for the less number of scans as compared to Case-2(small separation).Thus the CTTR performance in Case-1 (Fig. 7) is better in the measurement sharing region as compared to Case-2 (Fig. 10). The CSTTR in the Case-1 (Fig. 8) is also fast as compared to Case-2 (Fig.11). Case-1 confirms the split track at faster rate as compared to the Case-2.The RMSE is also affected in both the cases due to the different separation distances in both cases.
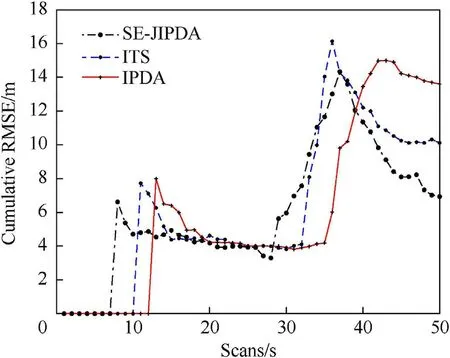
Fig. 12. Case-1: Cumulative RMSE of both parent and child track ρ= 10-6m-2 and Pd = 0.7.
3.4. Comparison with IPDA and ITS algorithms
Integrated track splitting (ITS) is a multi scan single target tracking algorithm.The ITS algorithm relates more number of scans to determine the target trajectory state estimate in the presence of clutter.
Integrated probabilistic data association (IPDA) is a single scan single target tracking algorithm. IPDA assumes point target assumption and merges all PDF’s as one Gaussian PDF in each scan.The single PDF propagates in the next scan for measurement selection and update process.
The proposed SE-JIPDA algorithm is compared with the IPDA and ITS algorithms. Results are presented in Figs. 12-13 for cumulative RMSE and CTTR for the Case-1, respectively. Similarly,Figs. 14-15 presents the results for Case-2 for both cumulative RMSE and CTTR, respectively. It is evident that SE-JIPDA performance is much better as compared to the IPDA and ITS algorithms in terms of RMSE and CTTR.
Split event true track rate (CSTTR) cannot be compared with both algorithms (ITS and IPDA) as they do not provide the procedure for split event detection and its state update.

Fig. 13. Case-1: Cumulative CTTR of both parent and child tracks ρ=10-6m-2 and Pd = 0.7.

Fig. 14. Case-2: Cumulative RMSE of both parent and child tracks ρ=10-6m-2 and Pd = 0.7.
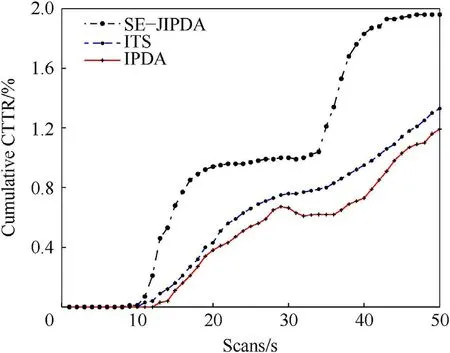
Fig. 15. Case-2: Cumulative CTTR of both parent and child tracks ρ= 10-6m-2 and Pd = 0.7.
4. Conclusion
In this work, split event detection and tracking algorithm is proposed in the presence of clutter. The proposed algorithm is termed as split event joint integrated probabilistic data association filter (SE-JIPDA). This algorithm provides a mechanism for split event detection and it tracks each split in the presence of clutter.The split event detection mechanism helps to monitor the performance of both the parent and split targets.
The performance of the proposed SE-JIPDA algorithm is compared with different algorithms under different simulation conditions.The results show a significant improvement in terms of true track rate and root mean square error performance compared to the existing algorithms. In the future, this work could be extended to multi-scan tracking algorithms and multiple model systems.
- Defence Technology的其它文章
- Development of cost effective personnel armour through structural hybridization
- Effects of jute fibre content on the mechanical and dynamic mechanical properties of the composites in structural applications
- Experimental research on the instability propagation characteristics of liquid kerosene rotating detonation wave
- Gabor-CNN for object detection based on small samples
- Integrated guidance and control of guided projectile with multiple constraints based on fuzzy adaptive and dynamic surface
- Strain concentration caused by the closed end contributes to cartridge case failure at the bottom

