Integrated guidance and control of guided projectile with multiple constraints based on fuzzy adaptive and dynamic surface

Shang Jiang , Fu-qing Tian, Shi-yan Sun , Wei-ge Liang

Naval Engineering University, Ordnance Engineering College, Wuhan, Hubei, China

Keywords:Integrated guidance and control Multiple constraints Fuzzy adaptive Dynamic surface Nonsingular terminal sliding mode Extended state observer

A B S T R A C T Based on fuzzy adaptive and dynamic surface(FADS),an integrated guidance and control(IGC)approach was proposed for large caliber naval gun guided projectile,which was robust to target maneuver,canard dynamic characteristics, and multiple constraints, such as impact angle, limited measurement of line of sight (LOS) angle rate and nonlinear saturation of canard deflection. Initially, a strict feedback cascade model of IGC in longitudinal plane was established, and extended state observer (ESO) was designed to estimate LOS angle rate and uncertain disturbances with unknown boundary inside and outside of system, including aerodynamic parameters perturbation, target maneuver and model errors. Secondly,aiming at zeroing LOS angle tracking error and LOS angle rate in finite time, a nonsingular terminal sliding mode (NTSM) was designed with adaptive exponential reaching law. Furthermore, combining with dynamic surface, which prevented the complex differential of virtual control laws, the fuzzy adaptive systems were designed to approximate observation errors of uncertain disturbances and to reduce chatter of control law. Finally, the adaptive Nussbaum gain function was introduced to compensate nonlinear saturation of canard deflection. The LOS angle tracking error and LOS angle rate were convergent in finite time and whole system states were uniform ultimately bounded, rigorously proven by Lyapunov stability theory. Hardware-in-the-loop simulation (HILS) and digital simulation experiments both showed FADS provided guided projectile with good guidance performance while striking targets with different maneuvering forms.

In recent years, the rapid developments of high-tech and advanced naval warfare theory have required the naval gun weapon to be capable of continuous naval surface fire support and accurate striking of maritime and coastal targets [1]. The naval gun guided projectile, rolling at low speeds during flight, not only possesses a higher firing speed,more ammunition carrying capacity and longer operation time than missile, but it also has a longer range, higher accuracy and superior cost-effectiveness compared with traditional ammunition, thereby providing effectively suppress and destroy fixed and maneuvering target near shore [2], and provide reliable naval surface fire support for amphibious forces.

Terminal guidance and control play a core role in achieving accurate strikes of naval gun guided projectile.With the upgrading of attack and defense equipment system, the relative movement speed between projectile and target increases, which makes the frequency of guidance close to that of control loop. Consequently,the frequency assumption of spectral separation might be invalid[3]. Due to the limited space in the control cabin of guided projectile, it is necessary for guidance and control loop to share sensors,such as gyroscopes and accelerometers,to promote economic efficiency and reliability. Furthermore, to achieve a better damage effect,multiple constraints existing in actual combat should be fully considered,such as impact angle[4],nonlinear saturation of canard deflection [5], canard dynamic characteristics [6], and limited measurement of LOS angle rate[7].Obviously,the traditional timescale separation design method and the method that merely meets miss distance constraint have difficulty adapting to aforementioned requirements,which attract experts,scholars and engineers to IGC method with multiple constraints.

The IGC, firstly proposed by WILLIAMS [8], essentially utilizes the coupling relationship between guidance and control system to construct a direct connection through aerodynamic angles and form a cascade closed-loop system. Based on the relative motion between projectile and target,the control law of canard deflection could be directly calculated by IGC algorithm. Since then, scholars have subsequently achieved results in IGC,combining with optimal control [9], robust control [10,14], back-stepping dynamic surface control [11,12,15], adaptive control [11,12,14], sliding mode control(SMC) [15-18], fuzzy control [18], and other modern control theories. Optimal control needs to solve complex Hamilton Jacobi Bellman (HJB) equation. Thereupon, VADDI [9] proposed an IGC design method based on nonlinear optimal control, which extended the linear control in the nonlinear system and reduced difficulty of solving HJB equation, and improved IGC performance through adopting Kalman filter to estimate target maneuver.However, computational complexity and multiple constraints should be considered.SONG[10]proposed a fast robust IGC design method for three-dimensional interception of hypersonic vehicle interceptor. The dynamic surface control was used to construct a robust compensation signal,which guaranteed fast convergence of LOS angle rate and strong robustness against uncertain disturbances. Nevertheless, its performance still depended on precise measurement of the LOS angle rate, which required too much for guided projectile in continuous rolling state.

Back-stepping control requires calculating high-order derivative of virtual control laws,which easily leads to differential expansion.Therefore, SEYEDIPOUR [11] designed a dynamic surface and introduced low-pass filter to avoid differential expansion, which simplified the design process by guaranteeing the guidance performance and system stability. Furthermore, with ESO combined,SHAO [12] designed a dynamic surface back-stepping controller.The model error, aerodynamic parameter perturbation, and other uncertain disturbances were observed by ESO, which significantly reduced the switching range of the dynamic surface.Owing to not considering the observation error term, the Proof of system stability needs to be improved. ESO, initially proposed by HAN [13],serves as a feasible scheme to figure out the time-varying nonlinear IGC problem with uncertain disturbances,whose simple algorithm could accurately observe the system states, internal and external disturbances without precise model of research object.

As the sole actuator of guided projectile,canard usually appears deflection saturation phenomenon, which makes available overload less than required overload,and easily leads to the system loss of control or even instability. Hence, WEN [14] designed adaptive Nussbaum gain function through combining adaptive robust control and back-stepping control, which effectively compensated the nonlinear saturation of actuator and stabilized the IGC cascade system.

Possessing strong robustness to the instability factors such as system parameters perturbation and external disturbances, SMC has been widely applied to IGC design, which is able to make the nonlinear dynamic system move along the pre-designed sliding surface. GUO [15] regarded the normal acceleration generated by target maneuver as a kind of disturbance, and designed the backstepping IGC method based on nonlinear dynamic sliding mode,which is robust to the uncertainty disturbances of target maneuver and missile model. To meet the terminal impact angle constraint,WU [16] defined the impact angle as the angle between projectile velocity and horizontal plane,and converted it into a standard form suitable for SMC through nonlinear transformation. Based on this,an IGC design scheme was proposed. However, it was pointed out that it is more universal to define impact angle as the angle between missile velocity and target velocity at the moment of impact[17], and the impact angle constraint could be converted into terminal LOS angle constraint. As we all know, it is chatter that is a difficult problem to be solved urgently in SMC,which c be partially improved by adopting continuous saturation function.Result from the difficulty of determining switching gains,the weakening effect of chatter is not satisfactory. Therefore, RAN [18] designed an adaptive fuzzy system by combining LOS angle rate and the distance between projectile and target to approach uncertain disturbances,which not only effectively weakened the chatter of control laws,but also improved the robustness of IGC.

In summary, IGC is a time-varying, nonlinear strict feedback cascade system with high order and multiple uncertainties.And the constraints mentioned above bring great challenge to the convergence and stability of IGC system in finite time. Therefore, the existing literatures mostly focused on sole constraint, while multiple constraints were closer to actual combat and more urgent to need to be solved. Fully considering multiple constraints and various types of uncertain disturbance and based on fuzzy adaptive and dynamic surface (FADS), this paper came up with a novel IGC design method against target with different maneuvering forms.Proven by Lyapunov theory,LOS angle tracking error,and LOS angle rate could converge in finite time, and whole system states were consistent ultimately bounded and arbitrarily small. To be more specific, the contributions of this paper could be highlighted as follows: 1) organically combining with dynamic surface, the fuzzy adaptive systems were designed,which not only effectively solved chatter of virtual control laws caused by difficulty in determining the switching gains, but prevented the differential expansion, 2)FADS was capable to guarantee the uniform ultimate boundedness of whole system states and the finite time convergence of LOS angle and LOS angle rate,and 3)the effectiveness and feasibility of FADS were verified by HILS, which could satisfy multiple constraints.

1. Model establishment

1.1. Motion and mechanical model

The relative motion relationship between projectile and target in longitudinal plane is shown in Fig.1, where Px0y0, Px1y1, Px2y2,Px6y6, Tx7y7, and Tx8y8represent projectile reference coordinate,projectile body coordinate, projectile trajectory coordinate, LOS coordinate, target reference coordinate, and target trajectory coordinate, respectively. Furthermore, P, T, r, and θQdenote projectile, target, distance between projectile and target, and LOS angle, respectively. aP,θP, vP, aT,θT, and vTdenote normal acceleration, trajectory angle, speed of guided projectile and target,respectively. In addition, θ, α, and δzrepresent pitch angle, attack angle,and pitch canard angle, respectively.

Assumption 1.Ref. [14] guided projectile could be regarded as rigid body,and target could be regarded as particle.r,θQ,θP,vP,and θ could be measured easily.P and T merely possess acceleration in the normal direction of respective velocity, which always satisfies vP>vT.

The relative motion relationship between projectile and target is given by:

Designating θQT=θQ-θT,θQP=θQ-θP,and the derivative of Eq. (1) could be obtained as follows:

With the first-order dynamic characteristics of canard considered,the dynamic model of naval gun guided projectile in longitudinal plane is as follows:

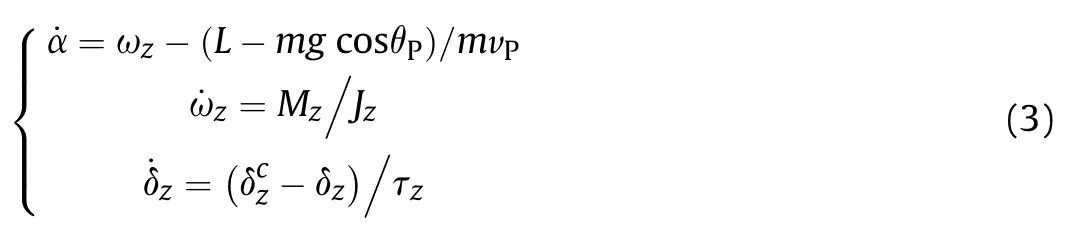
where ωz,L,m,Mz,and Jz,are pitch angular velocity,lift force,mass,pitch moment,and inertia transverse moment of guided projectile,respectively.and τzare control command and time constant of pitch canard, respectively. g is gravitational force acceleration.

Due to the rotation speed of guided projectile is low,the channel coupling factor caused by Magnus force and Magnus moment is such small that could be ignored,so L and Mzare given by:

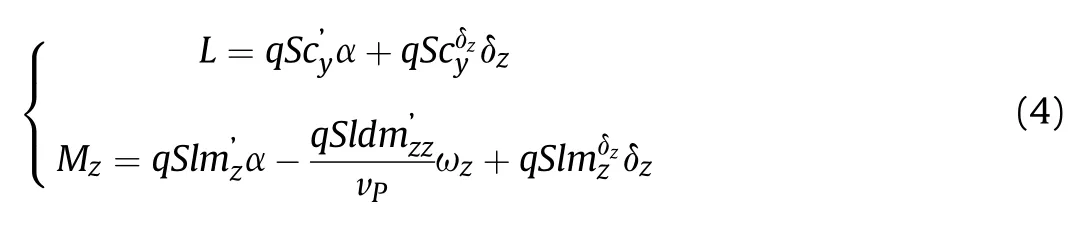
where q,S,d,and l are dynamic pressure,reference area,reference diameter,and reference length,respectively.andrepresent lift coefficient derivative and canard lift coefficient derivative, respectively.andare static moment coefficient derivative and equatorial damping moment coefficient derivative,respectively.

Assumption 2.[16] L is mainly produced by α, and the influence of canard deflection on L could be regarded as bounded uncertain disturbance.

1.2. Maneuvering target model

Note that the maritime and coastal maneuvering target could be approximately expressed by the following first-order term:

where τTandare time constant and normal acceleration command of target, which are obviously unknown and bounded.

1.3. Impact angle model

In the longitudinal plane, the expected impact angle ϑEis defined as the angle between vPand vTat the impact moment.Zeroing the relative normal velocity of projectile and target leads to

where θQfand θTfare the final LOS angle and final target trajectory angle, respectively, which could be acquired by unmanned reconnaissance. For any specified ϑE, there exists a unique θQfcorresponding to it[17],and impact angle constraint could be converted into LOS angle constraint.

1.4. System states space

The system states variables x1，x2，x3，x4，x5and control law u are defined as θQ-θQf，Q， α， ωz， δz, andrespectively. The state space of rigorous feedback cascade IGC system of guided projectile could be formulated as follows:

In Eq. (7), the functions f2（x2）, f3（x3）, f4（x3，x4）, f5（x5）, and parameters a2, a4, b are denoted as follows:

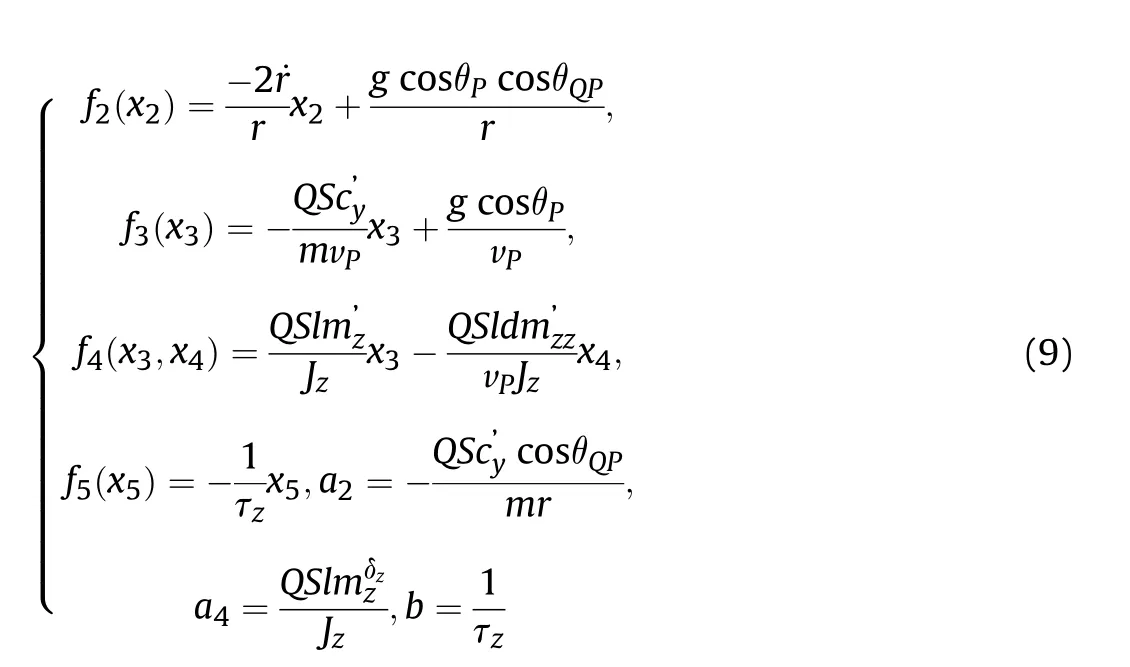
In Eq. (7), di（i=2，3，5） and d40are comprehensive disturbance terms with taking target maneuver, model error and aerodynamic parameter perturbation into account, which are specified as follows:

Fig.1. Relative motion relationship between projectile and target.

where Δ is the perturbation percentages of aerodynamic parameters,and die（i=2，3，4，5）are modeling errors.For the convenience of IGC design, a continuous differentiable hyperbolic tangent function vector ℘（x5） is introduced to describe canard deflection saturation.

Moreover, the IGC strict feedback state space of guided projectile could be expressed as follows:

where d4=d40+a4dsgis a comprehensive disturbance term, andFor the convenience of IGC design, the following reasonable assumption is given.

Assumption 3.[19] The comprehensive disturbance terms di（i=2，3，4，5） are bounded, i.e. there are unknown normal numbers dimaxsuch that satisfy |di|≤dimax.

Remark 1.The derivative of the disturbance terms di（i=2，3，5）are bounded.And according to the definition of d4,d4does not have intermittent points on the domain, which belongs to continuous function. But when x5= ±δmax, the left derivative and the right derivative of d4are not equal, so d4could be differentiable in definition domain except these two points,and the derivative of d4except these two points is obviously bounded.

2. FADS design

The purpose of FADS design is to generate an appropriate control law u for Eq. (12), which could make state variables x1and x2converge to any small neighborhood of zero in finite time, and guarantee whole system states are uniformly ultimately bounded and arbitrarily small, with limited measurement of x2, the saturation of x5,and the unknown bounded disturbance di（i =2，3，4，5）.

2.1. ESO design

In order to acquire accurate observation value of d2andquickly, the third order ESO is designed as follows, with the observational variables defined as zx1，zx2，zd2.

where β2i>0（i = 1，2，3）, η2i>0（i = 1，2）, 0<σ2i<1（i=1，2） and nonlinear function fal（e21，σ21，η21） is specified as

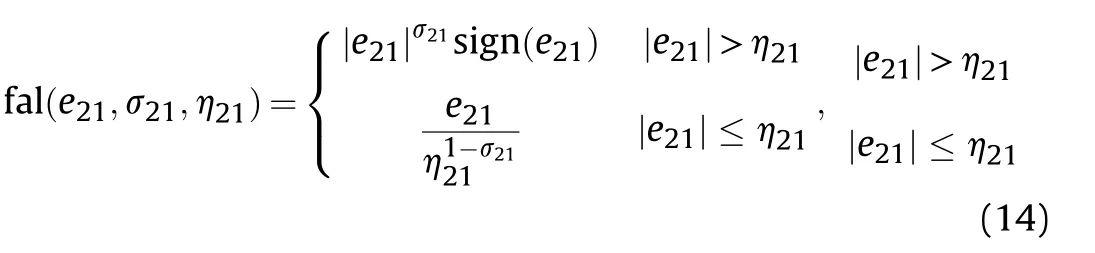
In Ref. [4],the stability of second and third order ESO designed in cascade systems were deduced and proven. By choosing appropriate parameters values,especially letting β23be much larger than β22and β21, the ESO given by Eq. (13) could observe d2accurately and quickly[20]. Similarly, for observing di, the observational variables are defined as zxi，zdi（i = 3，4，5）, the second order ESOs are designed as follows:

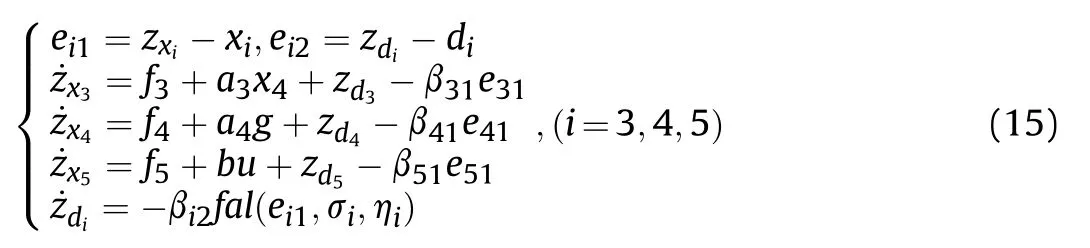
where the value range of each parameter is similar to Eq. (13).

2.2. Nonsingular terminal sliding mode design

Lemma 1.[21] Considering the following system:

where x∈Rnis the system state vector, g（x，t）: U0×R→Rnis a nonlinear continuous function defined on U0×R,and U0∈Rnis an open neighborhood of the origin x（t） = 0. Assuming V（x） is a C1smooth positive definite function defined on U∈Rnand（x）+CVA（x）is negative definite on U∈Rnfor C∈+and A∈（0，1）,then there exists an area U0such that any V（x） which starts from U0∈Rncould reach V（x）≡0 in finite time. Furthermore, if Tris the time needed to reach V（x）≡0,then x0）/［C（1 -A）］,where x0）is the initial value of V（x）.

A kind of NTSM is selected as follows:

where β>0 and 1<γ<2,and the time derivative of Eq. (17) could be obtained as follows:

To ensure well dynamic property in the sliding mode approach process, the sliding mode adaptive approach law is designed as follows:

where k2≥|e21| and c2>0. Combining Eq. (18) and Eq. (19), and removing the singular factors |x2|1-γ/βγ yields:

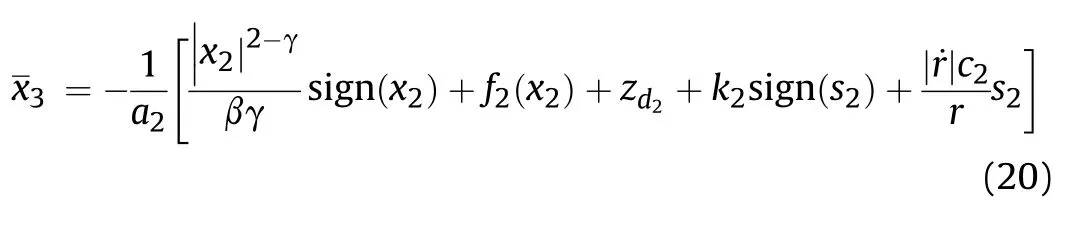
Theorem 1.For the subsystem constituted by the first two equations of Eq.(12),on the condition of adopting ESO given by Eq.(13)and control law given by Eq.(20),the system state variables x1and x2will converge to any small neighborhood of zero in finite time.

Proof.A Lyapunov function is chosen asand the time derivative of V2could be obtained as follows:

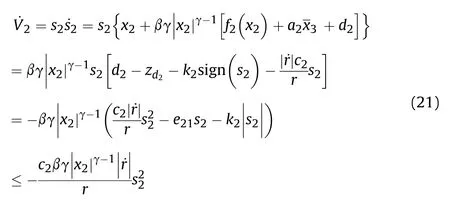
According to Lyapunov stability theorem, s2could converge to 0 in finite time while x2≠0, which is also satisfied if x2= 0 [22].Since then, one could be obtained as follows:

A Lyapunov function is chosen as, and the time derivative of Vx1could be obtained as follows:

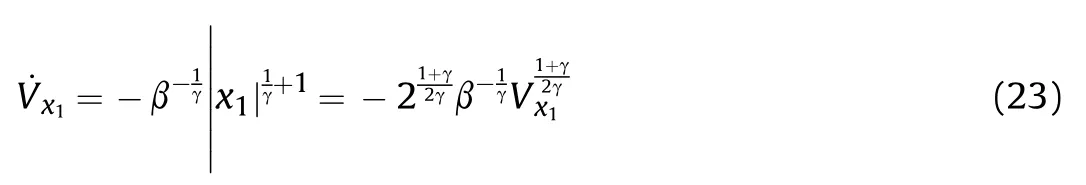
According to Lemma 1, one could be obtained x1and x2could converge to any small neighborhood of zero in finite time.The Proof ends.

2.3. Dynamic surface design

s2is defined as the second dynamic surface, and the third,fourth, fifth block dynamic surface are defined as follows:

To avoid direct differentiation with respect toare obtained through the following first order filter as follows:

where τ3,τ4, and τ5are positive constants.

Definition 1.[23] If the continuous function N（χ） satisfies the following property:then N（χ） is a Nussbaum function.

For handling the nonlinear saturation of canard deflection effectively, control laws are designed as follows:

where kiand ci（i=3，4，5）are positive parameters whose form and scope are similar to k2and c2,respectively.According to Definition 1, the following Nussbaum function is implemented:

where χ1and χ2are adaptive variables of Nussbaum function with the following adaptive law:

where γχis positive constant.

2.4. Adaptive fuzzy system design

Resulting from the time variability and nonlinearity of uncertain disturbances, it is difficult to determine appropriate switching gains,which causes serious chatter of the sliding mode.Possessing the universal approximation ability, the adaptive fuzzy system,composed of product inference, singleton fuzzification, centeraverage defuzzification, and Gauss membership functions, will be used to a.Thus,the high frequency chatter of the control law could be effectively weakened.

The input variable vector is defined as =［w1，…，wn］T∈Ω, then there arefuzzy rules in common as follows:

Lemma 2.[24]For a continuous function Γ defined on closed set⊆nand any precision ε,there must exist an adaptive fuzzy system Ξ（w|κ） composed of Eq. (31) and Eq. (32) such that satisfies

The optimal adaptive fuzzy parameters approximation vectors are defined as follows:

The approximation errors of fuzzy adaptive parameter vectors are defined asof which the adaptive approaching laws are as follows:

where λi>0, and the virtual control laws and control law are respectively modified as follows:

3. System stability analysis

Lemma 3.[26] Let V（t） and χ（t） be smooth functions, which are defined on［0，tf）with V（t）≥0.∀t ∈［0，tf）,and N（·）is a Nussbaum gain function. If the following inequality holds, then V（t） and χ（t）must be bounded on ［0，tf）:

where C>0 and M>0. The errors of the virtual control laws are defined as follows:

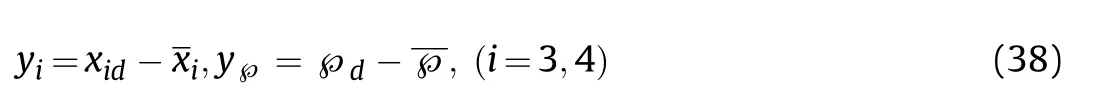
Differentiating xidand ℘dyields:

By simple simplification, we have

According to literature [22], there are positive real numbers Miandsuch that the inequalitieshold.Through some simple calculations, we have

Considering the following Lyapunov function of whole system states:

The dynamic surface vector is defined as =［s2，s3，s4，s5］T, of which the norm is defined as follows:

Theorem 2.For Eq.(12)that satisfies Assumptions 1～3,the whole system Lyapunov function V and whole system states are uniformly ultimately bounded and arbitrarily small, with the application of the ESO given by Eqs.(13)and(15),dynamic surface given by Eqs.(17) and (24), control law given by Eqs. (20) and (36), and appropriate parameters selected. And ||s|| satisfies the following inequality

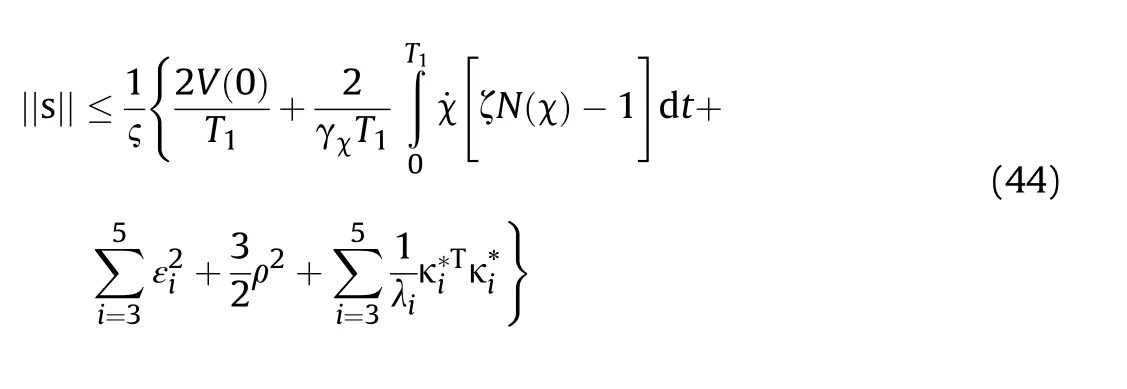
Proof.The derivative of V is:

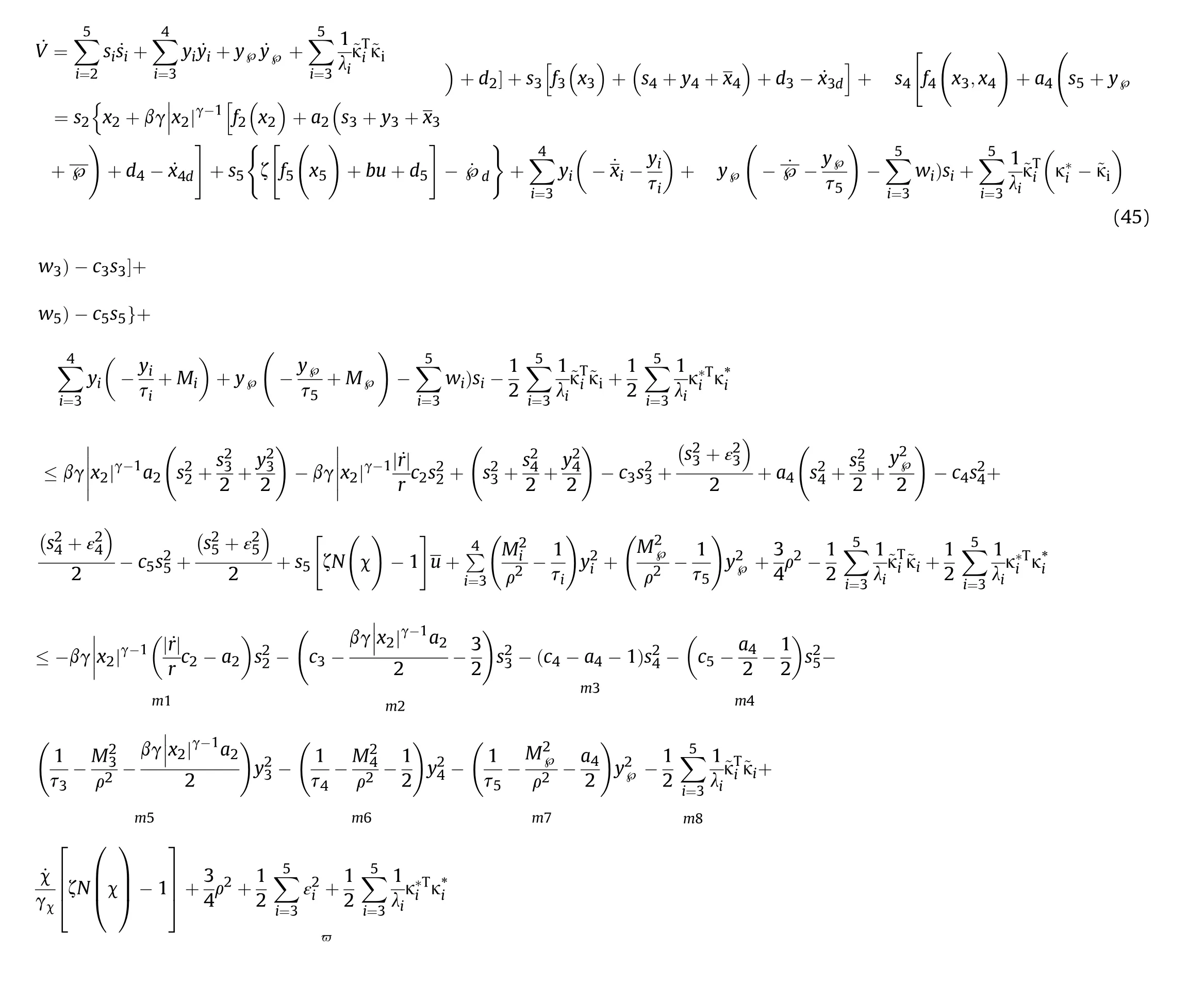
The appropriate parameters are selected to meet the following requirements, which could guarantee the system stability.

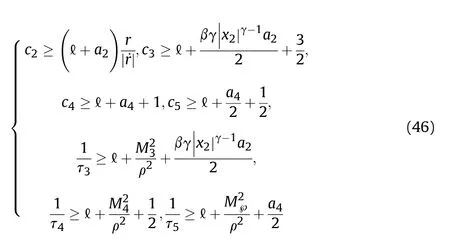
where ℓ is an arbitrary positive constant. Letting the positive constant ς =min｛mi（i =1，…，8）｝,then Eq.(45)could be simplified as

where the meaning of ϖ is detailed in Eq. (45). And by the comparison principle [24], it is easy to conclude from Eq. (47) that

According to Lemma 3 and Barbalat Lemma [18], V and system states are uniformly ultimately bounded and arbitrarily small.Moreover, one that could be obtained from Eq. (47)

Table 1 Main indexes of canard.

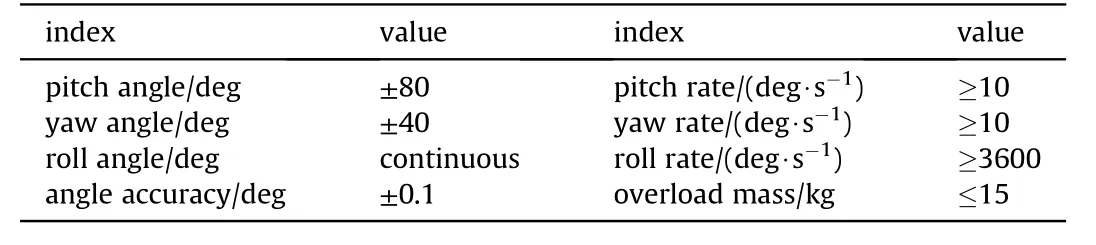
Table 2 Main indexes of turntable.

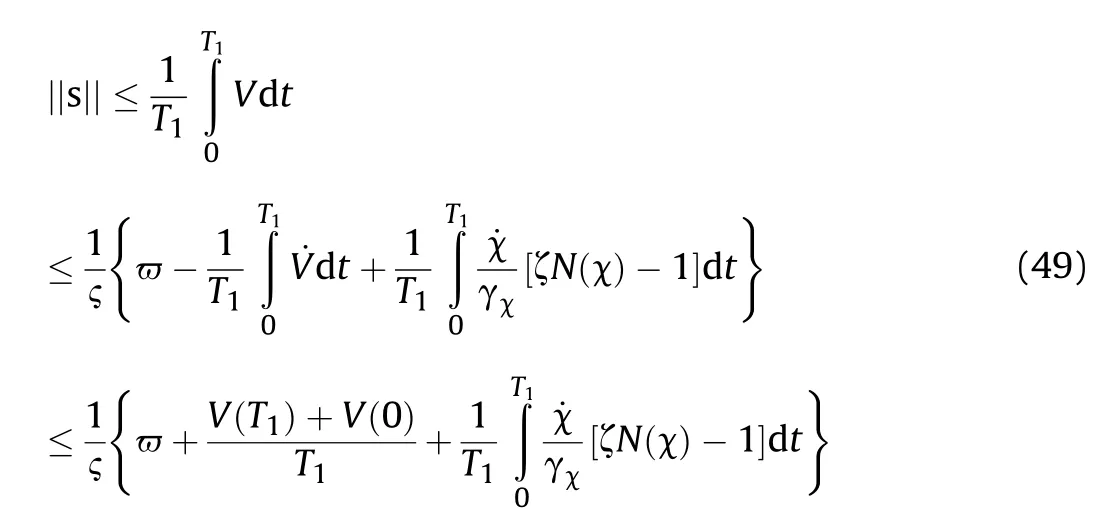
From Eq. (49), we have

Table 3 Parameters of projectile.

Table 4 Parameters of motion and system.

Table 5 Parameters of guidance and control.

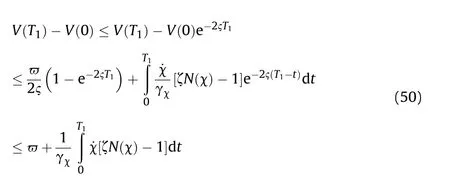
From Eqs. (48) and (50), one could be obtained

The Proof ends.Similar to the existing literatures[25],Theorem 2 shows the existence of the control algorithm to ensure the stability and convergence accuracy of the closed-loop system but does not provide a quantitative criterion on how to select the design parameters.In fact,it is difficult to give such a criterion.By far,the design parameters can only be selected by mathematical simulation.

Remark 2.The IGC design in lateral plane possesses the same system structure as the IGC in longitudinal plane. In essence, they all belong to high-order series nonlinear systems with matching and unmatching uncertainties. Therefore, the method designed in this paper could also ensure the stability of the system when applied to lateral plane.

4. Experimental results and discussions

To verify the effectiveness and feasibility of FADS, the control module of a naval gun guided projectile was selected as the controlled object,and the HILS system was built,as shown in Fig.2,which mainly included a system management computer,three-axis turntable,industrial personal computer(IPC), and control module,including micro control unit (MCU) and dual channel canard. The main performance indexes of canard and turntable are shown in Table 1 and Table 2,respectively,which met requirements of HILS.

Fig. 3. Experiment curves of operating condition 1.

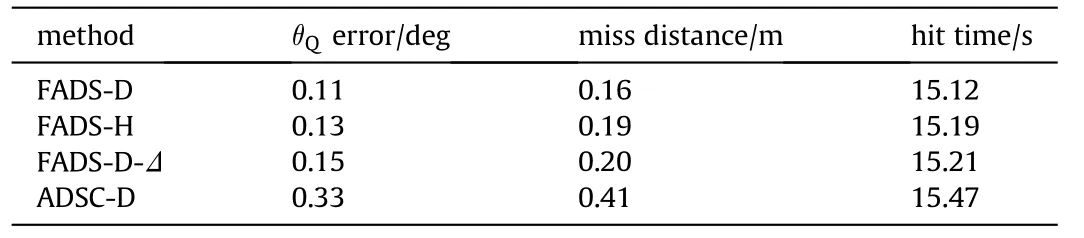
Table 6 Experiment results of operating condition 1.

The core component of the HILS system was the STM32F429IGT6 MCU, which configured the RS232 bus communication,interruption,direct memory access(DMA),and analog-todigital converter(ADC)according to the program compiled in Keil.The host computer controlled the states of the hardware-in-theloop simulation system by sending control instructions to the control module, such as the initial, start, stop, and recovery instructions. After starting the simulation, the MCU uses a Kalman filter to process the canard deflection feedback collected by ADC in real time and obtained attitude feedback from the IPC. These feedback parameters and the fourth order Runge-Kutta method were used to iterate the differential equations with a 10 ms step,which was composed of six-degree-of-freedom equations of the projectile, three-degree-of-freedom equations of the target, the relative motion equations, the Kalman filter, and AFCBDSM. The corresponding parameters were solved and sent back to the host computer. Meanwhile, the MCU sent the canard deflection and attitude commands to the dual channel canard and IPC, respectively.Based on the commands from the MCU,the canard drove its wings to deflect and the IPC drove the turntable to rotate. The simulation stopped until the distance between the projectile and target was less than the lethal radius. To ensure the efficient operation of the MCU and real-time communication between the devices,DMA was applied to the links with large amounts of data.

The parameters of projectile, motion and system,guidance and control were shown in Tables 3-5, respectively. In order to reflect FADS really doesn’t need x2, zx2is used in Eqs. (20) and (36). In addition,the radius of seeker blind area was set as 50 m,where the control law of canard deflection was unchanged and projectile relies on inertial flight. The initial values of adaptive fuzzy system parameters vectors κiwere 0, and the following Gauss fuzzy membership function was adopted:

To strike sinusoidal and square wave maneuvering targets, the HILS and digital simulation of FADS were carried out, with calibration and perturbation aerodynamic parameters considered.As contrast, the ADSC[25] was simulated numerically under same conditions, which used the following continuous saturation function instead of symbolic function to reduce chatter:

where δ is a positive constant.

Remark 3.Most of the existing HILS about guidance and control system are based on computer to complete core tasks, such as model solution and data interaction,whereas the HILS designed in this paper is based on the projectile borne MCU,which fully shows FADS proposed in this paper possesses well engineering effectiveness and practicability.

4.1. Operating condition 1: sinusoidal maneuvering target

The normal acceleration command of sinusoidal maneuvering target was set as=3 sin（t/4） （m·s-2）. The experiment results and curves were shown in Fig. 3 and Table 6, respectively, whereFADS-D,FADS-H,and ADSC-D represent digital simulation of FADS,HILS of FADS, and digital simulation of ADSC both in calibration aerodynamic parameters, respectively. And FADS-D-Δ represents digital simulation of FADS in 20% perturbation aerodynamic parameters.

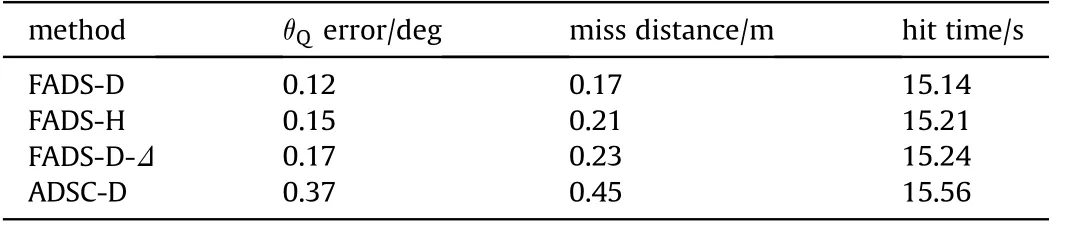
Table 7 Experiment results of operating condition 2.

From Fig.3(a),one could be observed both FADS and ADSC could be utilized in the terminal guidance stage of guided projectile while attacking square wave maneuvering target.And from Table 6,FADS optimized miss distance,hit time and θQtracking error,which was conducive to fine adjustment of guided projectile in terminal guidance process.

Fig. 4. Experiment curves of operating condition 2.

The trend of aPwas demonstrated in Fig. 3(b). With fixed gain parameters,ADSC relied merely on the dynamic surface to stabilize system, which caused the initial value to change greatly, the peak value to become large and the terminal convergence rate to be slow.On the contrary,FADS effectively weakened the chatter of dynamic surface by adaptive adjustment of fuzzy parameters, and terminal convergence rate was faster, which showed well robustness.

As could be seen from Fig. 3(c), it was easy for ADSC to appear saturation of canard deflection, owing to not take the nonlinear saturation of canard deflection into account. Moreover, under the disturbances internal and external of system,δzvaried widely and rapidly, which usually wasted precious energy, even might cause irreversible damage to canard. However, FADS could avoid similar situation, which indicated the effectiveness of adaptive Nussbaum gain function in dealing with control saturation of actuator.

Fig. 3(d) showed the change of θ is smooth and continuous during guidance process.And it also illustrated the pitch channel of turntable possesses good servo performance. Under the control of adaptive fuzzy systems and dynamic surface, FADS had not only faster convergence rate than ADSC, but smaller overshoot.

The change of θQwas shown in Fig.3(e).Under control of FADS,θQmaintained stable convergent state after 7 s, which not only indicated θQandwere able to converge to zero in finite time,but verified the correctness about the finite time convergent property of s2in Theorem 1.

Fig. 3(f) revealed well observational and robust property of the designed ESO,which could quickly provide accurate observation ofand uncertain disturbances for effectively hitting sinusoidal maneuvering target. Hence, projectile had the ability to provide sufficient available control command to compensate the internal and external disturbances of system, which was helpful to reduce the requirement about control capability of guided projectile.

4.2. Operating condition 2: square wave maneuvering target

The acceleration command of square wave maneuvering target was set as=3sign［sin（t/4）］（m·s-2）,and the experiment results and curves were shown in Fig. 4 and Table 7, respectively.

As shown in Fig. 4(a), the trajectory of projectile and target illustrated FADS and ADSC could both make guided projectile hit the sinusoidal maneuvering target. Combining with Table 7, one could be obtained the trajectory of FADS was flatter than ADSC,which further improved the miss distance,hit time,and θQtracking error, and was less affected by aerodynamic parameters perturbation. It showed adaptive fuzzy control effectively improved the terminal guidance performance.

The change of aPcould be analyzed from Fig.4(b).Due to ADSC merely used continuous saturation function with constant coefficients, the system disturbance items had not been effectively treatment, which leaded the chatter of dynamic surface and the peak value of aPwere obviously larger than FADS. Whereas, FADS made the change of control instructions smoother and converges near the end by adaptive fuzzy system and dynamic surface,which was more in line with the actual operational needs.

As shown in Fig. 4(c), through introducing the adaptive Nussbaum function, FADS effectively dealt with the nonlinearity saturation and protects canard better,so as to avoid failing to reach the tactical index due to canard deflection saturation,it was found the pitch channel of canard could meet requirements of the actual canard deflection in switching frequency and amplitude. Result from the adaptive adjustment of fuzzy parameters, FADS further ameliorated the range and mutation of δzcontrast to ADSC.

Through analysis of Fig.4(d),under control of FADS,the change of θ was smooth and continuous during the terminal guidance process. Adopting adaptive fuzzy system and dynamic surface,FADS had not only faster convergence rate than ADSC, but smaller overshoot. From another point of view, the pitch channel of turntable possessed good tracking characteristic.

Just as shown in Fig. 4(e), result from the disturbance terms aren’t handled, ADSC was greatly affected by the aerodynamic parameters perturbation, resulting in slowing the convergence rate.On the contrast, with adjusting the values of parameters through ESO and fuzzy adaptive system,FADS maintained θQin convergent state after 7s,which not only indicated θQtracking error andwas able to converge to zero in finite time, but showed the designed NTSM could converge in finite time.

Fig.4(f)showed the designed ESO possessed well observational and robust property. Even under the condition of fast change and wide range of disturbances, the ESO could observeand disturbances quickly and accurately,which provided necessary feedback information.

5. Conclusion

Aiming at the terminal guidance stage of hitting coastal maneuvering target,the FADS was designed for large caliber naval gun guided projectile,with multiple constraints considered.It was theoretical Proof, digital simulation and HILS that both indicated FADS possessed well terminal guidance performance:

1) The designed adaptive dynamic surface avoids differential expansion,and the chatter of virtual control laws,caused by the difficulty in determining switching gains, were effectively solved by fuzzy adaptive systems.Moreover,the introduction of the adaptive Nussbaum function obviously improved the nonlinear saturation of canard deflection.

2) FADS was capable to guarantee the uniform ultimate boundedness of whole system states and the finite time convergence of LOS angle and LOS angle rate. Not only did it not need to measure LOS angle rate,but other required external information could be measured by mature technologies easily.

3) The effectiveness and feasibility of FADS, which had certain theoretical and engineering value, are validated through HILS,and possesses well engineering effectiveness and practicability.

Declaration of competing interest

No.

Acknowledgments

This work was supported by Naval Weapons and Equipment Pre-Research Project (Grant No.3020801010105).