“分数问题”教法初探
邵秀良

“分数问题”是小学阶段数学教学的重要内容和难点。在教学过程中,教师应注重对问题解决的研究,发展学生思维,提升学生解决分数实际问题的能力。
一、找准单位“1”,明确分数的意义
找单位“1”是解分数问题的基础与关键,只有找准了单位“1”,才能明确题中每个分数所表示的具体意义,才能清楚题目的数量关系,找到解决问题的方法。
例如:教学“儿童体内水分约占体重的[45]”这道题时,如果学生能知道把体重看作单位“1”,[45]表示把体重平均分成5份,则体内水分占其中的4份,那么关于体内水分和体重之间的关系学生就明白了。再如“一条公路已经修了[23]”这个题干,教学中应该让学生明确是把一条公路全长看作单位“1”,这里的[23]表示把这条公路全长平均分成3份,已经修的米数占其中的2份。这样学生就能在充分理解题意的基础上去分析题意。又如:(1)一根绳子3米,用了它的[12],还剩几米?(2)一根绳子3米,用了[12]米,还剩几米?遇到这样的问题时,要引导学生理解题中两个分数对应的单位“1”是不同的,两个分数所表示的意义也是不同的,题(1)是把一根绳子3米看作单位“1”,用了3米的[12],而题(2)是把1米看作单位“1”,用了1米的[12],所以两根绳子剩下的米数是不同的。在教学分数解决问题之前,让学生先明确题中单位“1”的量及每个分数表示的意义是必不可少的环节。
二、利用线段图,数形结合
在教学分数解决问题时运用线段图,能让学生很直观地看出两种量的关系,便于学生清楚地找出数量之间的关系,帮助学生理解题意,分析数量关系,拓宽解题思路,找到解决问题的方法。
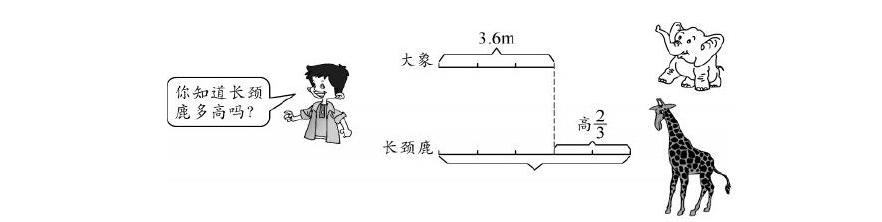
例如:大象高3.6米,長颈鹿的身高比大象多[23],求长颈鹿的高度。在学生明确了单位“1”和分数[23]表示的意义后,运用线段图帮助学生分析题意,寻找解题方法。此时,教师可以出示下图:
从图中学生就能直观地发现:长颈鹿比大象高,可以先求多出的高度,再求总的高度,即3.6+3.6×[23]。
三、抓住关键句,列出数量关系式
解决分数问题中的两个量属于整体与部分或者不同的数量间的相比较关系时,如果能抓住题中的“关键句”进行分析,从“关键句”中找出单位“1”和“相关联的两个量”,明确“相关联的两个量”之间的关系,根据分数乘法的意义写出关系式,那么分数问题是很容易得到解决的。
如“美术书本数比科技书多[34]”,这句话的意思是美术书比科技书多的本数占科技书的[34],这里把“科技书本数”看作单位“1”,美术书本数和科技书本数是相关联的两个量,结合前面讲的线段图得到它们的数量关系式是“科技书本数+科技书本数×[34]=美术书本数”。如果“已知科技书56本,求美术书本数”,从关系式中很容易求出美术书本数是56+56×[34];如果“已知美术书98本,求科技书本数”,从关系式中很容易列出方程x+x×[34]=98。因此,只要对比这两种题目的数量关系式,就能看出它们具有紧密的联系,区别主要是看单位“1”的数量原来是已知的还是未知的。
四、对比练习,掌握多种方法
分数解决问题的掌握对小学生来说比较难,需要经过一个反复调整的过程。教师在教学中适量安排一些对比性的练习,有利于学生形成清晰地找出单位“1”和数量关系式的基本思路和方法。
例如:(1)一个工厂有煤1250吨,用去500吨,还剩下几吨?一个工厂有煤1250吨,用去[35],还剩下几吨?这样的设计能使学生借助整数的数量关系再结合分数的意义,进一步理解分数解决问题的一般方法。再如:(2)修一段公路20千米,第一天修了全长的[14],①第二天修的米数是全长的[25];②第二天修的米数是第一天的[310],③第二天修的米数是余下的[45],④第二天比第一天多修[15],⑤第一天比第二天多修[110],求第二天修的米数。这样的题目能使学生在同一情境下理解不同单位“1”解决问题的不同方法,防止学生解决这类问题时死记方法,生搬硬套,达到真正掌握和提高的目的。
(作者单位:襄阳市襄州区张家集镇宋营小学)
责任编辑 张敏

