“数与代数”教学如何培养数学学科核心素养

姜楚华

“数与代数”是小学数学的核心内容之一，涉及“数的认识”“数的运算”“式与方程”“正比例、反比例”“探索规律”等内容。发展和培养数学学科核心素养，是“数与代数”教学的核心目标之一。

一、在“数的认识”教学中发展学科核心素养

素养蕴含在过程中，只有经历过程，才能培养学生的素养。

（一）经历数概念的抽象过程、运算过程，发展数学抽象素养、运算能力

数学抽象具有不同的阶段性。在小学数学教学中，数概念的抽象可以从实物抽象→替代物抽象（亦称半抽象）→符号抽象（符号化）逐级进行。之所以分层分级抽象，一方面是由小学生的认知水平决定的，另一方面是逐步培养学生数学抽象素养的需要。在小学一年级“数的认识”起始教学中，“经历从日常生活中抽象出数的过程，会数1～5个物体的个数，会用1～5表示物体的个数，知道1～5的顺序，并会认、读、写1～5”作为课程教学目标，其中，“经历从日常生活中抽象出数的过程”是素养培养目标，其直接目的是培养数学抽象素养;而“会数1～5个物体的个数，会用1～5表示物体的个数，知道1～5的顺序，并会认、读、写1～5”则是知识技能目标要求。如果省略“经历从日常生活中抽象出数的过程”，而采用死记硬背的方式直接让学生达成知识技能目标，的确可以“速成”，但是学生未必能够获得深度理解，更重要的是，学生丧失了一次发展数学抽象素养的良机。

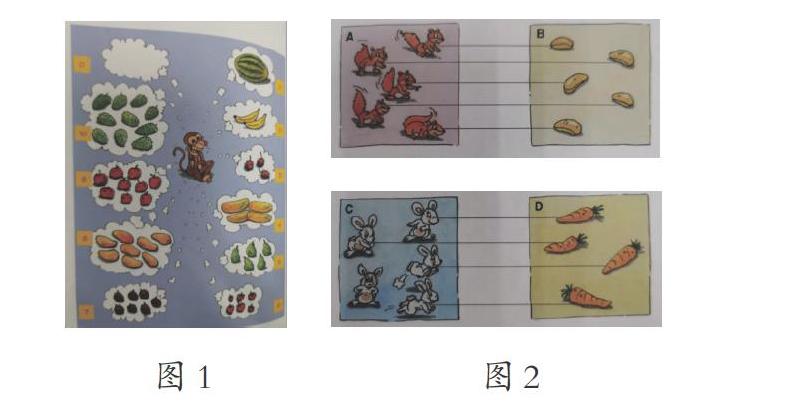
【案例1】新加坡小学数学教材“1～10的认识”教材内容

如下图，情景图1是实物直观，从实物1个西瓜、2根香蕉、3粒桑椹、4个香瓜、5个鸭梨、6颗樱桃、7个浆果、8个芒果、9个柿子、10粒草莓、0个（空无所有）水果之中抽象出数字1、2、3、4、5、6、7、8、9、10、0。

情景图2采用实物直观、利用连线方式体现数字的基数属性，即“松鼠”“坚果”两个集合一样多，都是5个（元素），从中抽象出数字5。

只有帮助学生亲身经历一个一个地数1个西瓜……0个水果的过程，亲身经历“5只松鼠吃坚果，刚好每只一个坚果;5只米老鼠吃胡萝卜，4个胡萝卜不够吃——有一只米老鼠没有吃到胡萝卜”的过程，积淀“数”的直接经验，才能逐渐形成初步的数学抽象素养。

（二）把握数学本质，感悟十进制中所蕴含的数学思想

小学“数的认识”包含自然数、整数、分数、小数。学习“数的认识”，并非仅仅让学生掌握相应的知识和技能，而是要引导他们经历抽象、运算与建模等过程，在掌握基础知识、基本技能的同时，体验基本数学思想、积淀直接的数学活动经验，发展数学学科核心素养。

以“自然数的认识”为例。在自然数的抽象过程中，理解作為基数的自然数和作为序数的自然数是主要目标，而识别、读写自然数是学习目标之一。

【案例2】小学数学人教版（生本学材2019年版）0～5的认识（数字1、2、3、4、5的抽象过程）

图3清晰地表达了作为基数的1、2、3、4、5的抽象过程：从1头狮子、1只老虎之中，抽象出1个点，表达数量1，进而抽象出数字1，这个过程本质上是狮子的集合与老虎的集合等价，表达它们共同属性的量是1;同样，企鹅的集合与青蛙的集合等价，表达它们共同属性的量是4;天鹅的集合与海豚的集合等价，表达它们共同属性的量是5。

图4则比较清晰地表达了1、2、3、4、5的序数的属性，刻画了数“数”的详细过程。卡通人物机器人说的话强化了学生亲身操作的过程：1+1=2表达“1的后继数是2”，2+1=3表达“2的后继数是3”，3+1=4表达“3的后继数是4”，4+1=5表达“4的后继数是5”。其数学原理是皮亚诺公理体系——自然数的序数理论。

与案例1新加坡小学数学教材相比，新加坡小学的数学教材虽能体现出数字1、2、3、4、5的基数属性，但并未充分体现出数字的抽象过程，人教版（生本学材2019年版）既能鲜活地体现数字1、2、3、4、5的抽象过程，又能将数字1、2、3、4、5的基数属性和序数属性体现出来，而只有帮助学生亲身经历数字抽象的过程，才能形成初步的数学抽象素养。不仅如此，在“自然数的认识”中，十进制中蕴含着深刻的数学思想，虽然自然数无穷无尽，但仅用有限的10个数码0、1、2、3、4、5、6、7、8、9和数位就可以表达。用有限的符号表达无限的元素是数学结构的典型特征，帮助小学生初步感知这种思想，有利于他们更深刻地体会“化繁为简”“追求简捷有序”的数学思维特点，间接地培养数学抽象素养。

二、在“数的运算”教学中培养数学核心素养

（一）在运算法则的形成过程中发展数学推理素养、数学抽象素养

“数的运算”涵盖自然数、整数、小数、分数四则运算，运算法则是其中的核心内容。采取归纳方式教学运算法则，可以有效培养学生的数学推理素养。

【案例3】交换率a+b=b+a的归纳式教学

（1）教师引导学生分析1+2与2+1、3+5与5+3，归纳得出1+2=3、2+1=3，1+2=2+1以及3+5=5+3等。由此提出猜想，a+b与b+a应该相等。

（2）如图5所示，教师站在学生中间，左手拿a支铅笔，右手拿b支铅笔，教师左边的学生看到的是从后向前数，即a+b支铅笔，教师右边的学生看到的从前向后数，即b+a支铅笔。同一组物品，从不同的角度看到的结果不同，但都是“加”。

（3）阐述“加”的含义——将两组物体a支、b支合放在一起，“不是你吞并我，也不是我吞并你，而是合在一起组成一个新的整体”，从而，从正面和背面看到的结果是一致的，这就是5+4=4+5，一般情况是a+b=b+a。

【案例4】自然数乘法法则的抽象过程

图6是新加坡教材中表达的乘法2×5=10的抽象过程。用苹果图片代表红苹果，每组图片包含5个苹果，共两组，一共多少个苹果，是实物层面的抽象。在数轴线上表达上述过程，即：每个格代表1个苹果，5个格代表5个苹果，两组就是“每次跳5个格、连续跳两次”，到达第10个格。这是替代物层面的抽象。经过两次抽象之后，苹果的其他属性全部被剥离，仅剩下数量这个属性了，数数轴上的格子即可发现一共10个。用数学符号表达上述过程，即2×5=10，这是符号层面的抽象。

帮助学生完整地经历实物层面的抽象→替代物层面的抽象→符号层面的抽象的2×5=10的抽象过程，而不是直接给出2×5=10的结果，不仅能帮助学生获得对乘法法则的深刻理解，而且引导他们经历了数量关系的抽象过程，发展了学生的数学抽象素养。

（二）在“数的运算”教学中培养数学抽象素养、数学运算能力和直观想象素养

第9期文章介绍了借助“10个鸡蛋一盒”学习“两位数加一位数的进位加法”的案例。实践表明，借助生活中的一整盒的经验，绝大多数学生能自然地想到将空出的3个位置补齐凑成一整盒，这样计算最方便，这就是“将4拆成3和1，3与27凑成3整盒”最朴素的思想来源。这个教学过程的核心是帮助学生将生活经验变成数学经验，让他们在经历数学逐级抽象的过程、在习得数学知识技能的同时，获得数学抽象、直观想象的经验，既理解知识，又提升数学抽象能力和运算能力。

（三）在“数的运算”“式与方程”“正比例、反比例”教学中突出数学建模过程，培养初步的数学建模素养

小学“数的运算”中包含有两个重要数学模型，一是加法模型，另一个是乘法模型。“式与方程”“正比例、反比例”中包含方程模型、乘法模型等模型。帮助学生经历数学建模的完整过程，才能逐步培养学生的数学建模素养。

【案例5】加法模型

人教版（生本学材2019年版）B版“6的认识”中出示的这个情景（如图7），需要逐层分析。

（1）发现问题：从荷叶情景图中，你能读出哪些信息？

（2）提出数学问题：①一共有几只青蛙？②跳入水中之后，还剩下几只青蛙？③青蛙比蜻蜓多几只？

（3）分析、解决问题：①荷叶上有4只青蛙，有2只青蛙即将跳入水中，一共有4+2（只）青蛙。②一共有6只青蛙，有2只即将跳入水中，跳入水中之后还剩下6-2（只）青蛙。③有6只青蛙，4只蜻蜓，青蛙比蜻蜓多6-4（只）。问题①实际上利用了“部分量之和是总量”的加法模型;问题②实际上利用了“部分量之和是总量”的加法模型的变形;问题③实际上利用了“部分量之和是总量”的加法模型的变形。

案例5中，如果教学仅仅定位在“认识6”、获得6的分解和组合，那么教学目标就只是知识技能目标，明显是不科学的，因为渗透“加法模型”、培养初步的数学建模素养，也是小学一年级数学可以实现的目标。同样的，“式与方程”“正比例、反比例”的教学也需要帮助学生经历模型的构建过程。如，方程模型的建构，要经历“发现现实问题中的量及量与量之间的等量关系[？]用自然的语言表达等量关系[？]用半符号语言或直接用符号语言表达等量关系[？]用含有未知数的式子ax±b表达等量关系”的过程，而不是直接设未知数为x，得到方程ax±b=c。

三、在“数的运算”综合运用、“探索规律”、“式与方程”和“正比例、反比例”中发展数学推理能力、运算能力

推理是数学的基本思维方式，推理能力的发展应贯穿在“数的认识”“数的运算”“式与方程”“正比例、反比例”等的教学中，而在“探索规律”和“数的运算”综合运用中更加突出。

（1）计算下列三个算式，你有什么发现？

（2）用刚才的发现，先猜一猜45×11的积是多少，再用竖式实际算一算，看看你的猜测是否正确、是否需要修改你的猜测，最后用11×63、11×87再验证你修改后的结论。

（3）总结你的发现，说一说其中的道理。

尝试着验证猜测，就不再是两位数乘两位数乘法的简单重复训练了，而变成螺旋上升、呈梯度深化的归纳推理的训练：学生从10×11=110，14×11=154，16×11=176中，似乎可以得出“乘积是三位数，百位都是1，十位数字是第一个因数两个数位数字之和”;当学生分析45×11=495后，往往会修改自己的猜测，部分学生马上得出“两边一拉，中间一加”的猜测，即“将乘数45的两位数字一拉，中间放上这两个数字之和4+5，即9，得到的数字495就是乘积”;同时，还可以用11×63或者自编题目，如11×87、11×75等，验证自己的“发现”，即先猜11×63是多少，再用列竖式计算的方法加以验证。当学生用11×87验证时就会发现，8与7之和“”已超过10，此时，结果还是87吗？从字面分析，如果还是这个规律，那么，结果一定是8157，而11大约是10，87大约是90，二者的乘积是90×10=900左右，绝不可能是8000多的值。猜想此时不成立！

仔细分析可以发现，如果两数字之和大于10，而十位数字上的一个十相当于一个百，此时应将8与7之和的十位数值1进到百位数值8上，即此时应该是957。利用竖式笔算计算11×87可以验证，积的确是957。于是，上面的规律应该修正为：×11，积是“两边一拉，中间一加，如果加的结果不超过10，积就是将加的结果放在百位所得的数字，如果中间加的结果超过10，需要将所得的十位数字进到百位上”。

这种设计的真正意图在于，在巩固“两位数乘两位数”基础知识、基本技能的过程中，让学生经历归纳、猜测的思维过程，获得“个案1、……、个案n→归纳出一个共性规律，猜测→验证自己的猜测→得出一般结论”的直接经验和体验，经历一次“数学家式”的思考过程，体验创新的快乐，而教学不是在知识技能的简单重复上下功夫，而是按照知识技能的复杂程度、学科思维的深广度、待解决问题的繁难程度等多条线索交替螺旋上升，进而让学生获得知识技能形成的经验、独立思考的经验、猜测发现的直接经验和体验，培养数学推理能力。

【案例7】月历中的规律

在2020年10月月历中：

（1）任意圈三行三列（如上表中的绿色方框）包含9个数，它们的和是多少？你能推断任意一个这样的方框之中9个数之和的一般计算方法吗？

（2）如果任意圈两行两列四个数字，比如上表中的黄色部分，它们对角交叉相乘的积的差是多少？你能推断任意一个这样的方框之中4个数对角交叉相乘的积的差的一般计算方法吗？

问题（1）中，表中绿色方框中的9个数字的和是126，即中間格子中的数14与9相乘的积。若用a表示方框中间的数，则方框中的所有数可以表示为下表所示的情形：

[a-8    a-7 a-6 a-1 a   a+1 a+6 a+7 a+8 ]

很显然，这9个数的和（a-8）+（a-7）+（a-6）+（a-1）+a+（a+1）+（a+6）+（a+7）+（a+8）等于9a，是最中间的数字a的9倍。因此，我们判断，任意一个这样方框中的9个数的和都是中间这个数字的9倍。

问题（2）中，对角交叉相乘的积的差是7，即4×10-3×11=7。再换另外一组试一试，比如14、15与21、22，结果是15×21-14×22=7，规律依然成立。验证这个猜想需要寻找普适性的规律，即引入字母表达任意的数。设任意圈的两行两列（包含4个数字）的第一个数字为b，那么，另外的三个数字必定为b+1、b+7、b+8，于是，交叉相乘的结果是（b+1）（b+7）-b（b+8）=bb+b+7b+7-bb-8b=7，结果的确与b的取值无关。

用字母表示是由特殊到一般的过程，而由字母求值、利用数学公式求值，是从一般到特殊的过程。它可以帮助学生进一步体会字母表示的意义，发展学生“从事物的具体背景中抽象出一般规律和结构，并用数学语言予以表征”的本领。这种成分就是数学抽象素养的重要组成部分。

[本文是中南民族大学2019年校级重点教研项目《卓越小学教师课程体系改革实践研究》（项目序号：JYZD19034）成果]