“勾股定理”优题库

刘东升

1.将面积为8π的半圆与两个正方形拼接，如图l所示，这两个正方形面积的和为（）.

A.16    B.32    C.8π    D.64

2.如图2，△ABC中，∠BAC=90°.点A向上平移后到点A，得到△A'BC.下列说法中错误的是（    ）.

A.△A'BC的內角和仍为180°

B.∠BA 'C<∠BAC

C.AB²+AC²=BC²

D.A'B²+A'C²2

3.如图3，0为数轴原点，A，B两点分别对应-3，3.作腰长为4的等腰△ABC，连接OC.以O为圆心，OC长为半径画弧，交数轴于点M，则点M对应的实数为（    ）.

A.√7、    B.4    C.5    D.2.5

4.如图4，小明将一张长为20 cm，宽为15 cm的长方形纸片（AE>DE）剪去了一角，然后量得AB=3cm，CD=4cm.剪去的直角三角形的斜边长为（    ）.

A.5cm  B.12cm  C.16cm  D.20cm

5.如图5，在2x2的正方形网格中，每个小正方形的边长为1，点A，B，C均为格点，以点A为圆心，AB长为半径作弧，交格线于点D.则CD的长为（    ）.

A.1/2  B.1/3  c.√3  D.2-√3    2    3

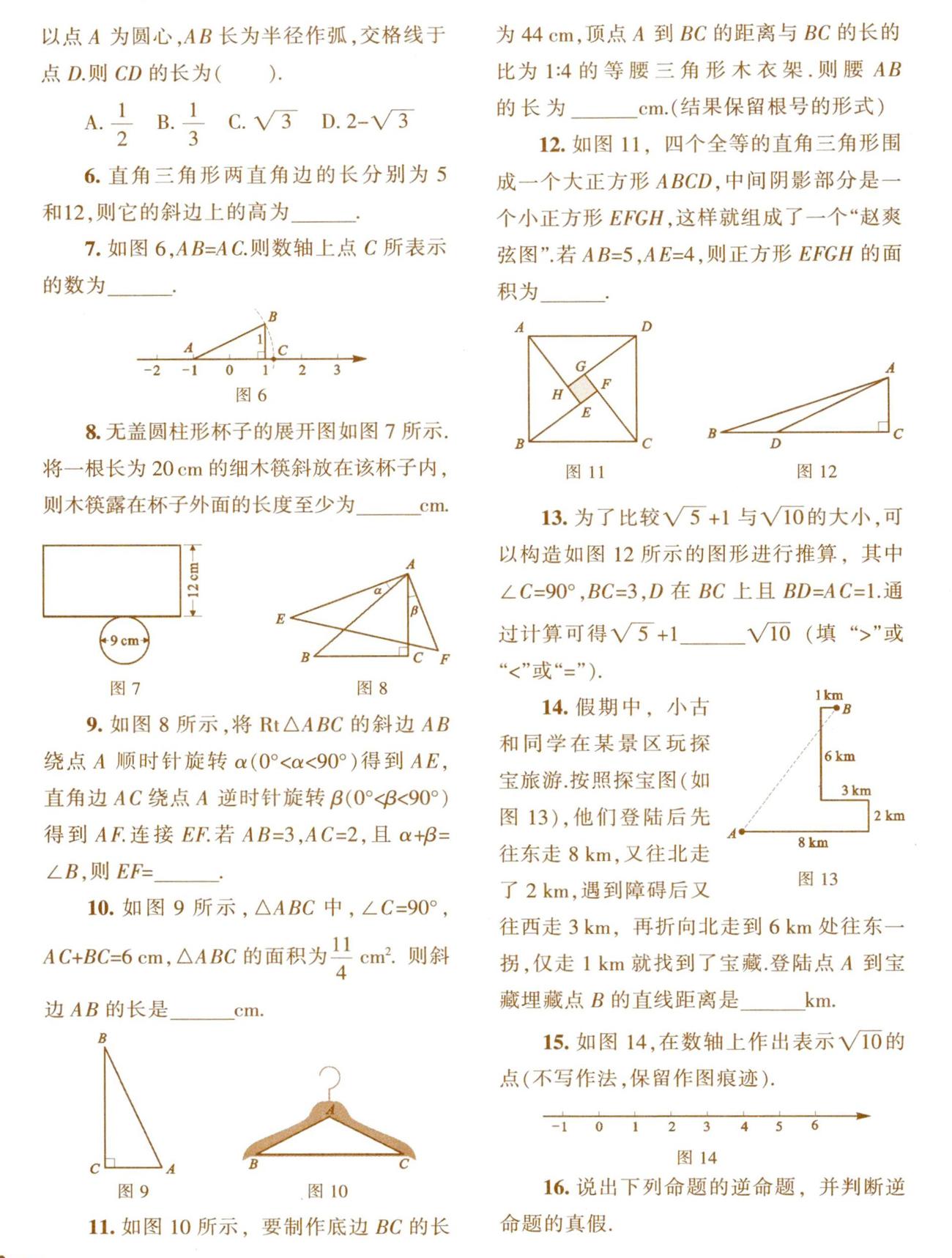
6.直角三角形两直角边的长分别为5和12，则它的斜边上的高为______.

7.如图6，AB=AC则数轴上点C所表示的数为________.

8.无盖圆柱形杯子的展开图如图7所示，将一根长为20cm的细木筷斜放在该杯子内，则木筷露在杯子外面的长度至少为______cm.

9.如图8所示，将Rt△ABC的斜边AB绕点A顺时针旋转a（0°

10.如图9所示，△ABC中，∠C=90°，AC+BC=6cm.△ABC的面积为11/4 c㎡，则斜边AB的长是______cm.

11.如图10所示，要制作底边BC的长为44cm，顶点A到BC的距离与BC的长的比为1：4的等腰三角形木衣架，则腰AB的长为______cm.（结果保留根号的形式）

12.如图11，四个全等的直角三角形围成一个大正方形ABCD，中间阴影部分是一个小正方形EFGH，这样就组成了一个“赵爽弦图”.若AB=5，AE=4，则正方形EFGH的面积为________.

13.为了比较√5+1与√10的大小，可以构造如图12所示的图形进行推算，其中∠C=90°，BC=3，D在BC上且BD=AC=l.通过计算可得√5+1√10（填“>”或“<”或“=”）.

14.假期中，小古和同学在某景区玩探宝旅游.按照探宝图（如图13），他们登陆后先往东走8km，又往北走了2km.遇到障碍后又往西走3km，再折向北走到6km处往东一拐，仅走1km就找到了宝藏，登陆点A到宝藏埋藏点属的直线距离是______km.

15.如图14.在数轴上作出表示√10的点（不写作法，保留作图痕迹）.

16.说出下列命题的逆命题，并判断逆命题的真假.

（1）内错角相等，两条直线平行;

（2）如果两个实数相等，那么这两个实数的立方相等：

（3）角的平分线上的点到角的两边的距离相等：

（4）直角三角形中，30°角所对的直角边等于斜边的一半.

17.如图15，在Rt△ABC中，∠ACB=90°，AC=16，AB=20，CD⊥AB于点D.

（1）求BC的长;

（2）求CD的长.

18.如图16，在Rt△ABC和Rt△BDE中，∠C=90°，∠D=90°，AC=BD=a，BC=DE=b，AB=BE=c.点B，C，D在一条直线上，试利用该图形证明勾股定理.

19.学习了勾股定理后，我们都知道“勾三股四弦五”.观察3，4，5;5，12，13;7，24，25;9，40，41……可以发现这些勾股数的“勾”都是奇数，且从3起就没有间断过.

（1）请你根据上述规律写出下一组勾股数：______.

（2）若第一个数用字母n（n为奇数，且n≥3）表示，那么后两个数用含n的代数式可分别表示为______和______，请用所学知识说明它们是一组勾股数.

20.大家都见过形如x+y=z这样的三元                  x=3，

一次方程，并且知道y=4，就是适合该方程                  z=7，

的一个正整数解，法国数学家费马在17世纪还曾研究过形如X²+y²=z²的方程.

（1）请写出方程X²+y²=z²的两组正整数解：_______，_______.

（2）解完（1）后，你想起了什么？

21.在△ABC中，AB=15，BC=14，AC=13.求△ABC的面积.

某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路完成解答过程.

（l）如图17，作AD⊥BC于D.设BD=x.用含x的代数式表示CD.

（2）根据勾股定理，利用AD作为“桥梁”，建立方程模型，求出x.

（3）利用勾股定理求出AD的长，再计算三角形的面积.

22.在△ABC中，BC=a，AC=b，AB=c.设c为最长边，当a²+b²=C²时，△ABC是直角三角形;当a²+b²≠C²时，利用代数式a²+b²和C²的大小关系，探究△ABC的形状（按角分类）.

（1）当△ABC的三边长分别为6，8，9时，△ABC为______三角形;当△ABC的三边长分别为6，8，11时，△ABC为____三角形.

（2）猜想：当a²+b²_______C²时，△ABC为锐角三角形;当a²+b²______C²時，△ABC为钝角三角形.

（3）试判断当a=2，b=4时△ABC的形状，并求出相应的c的取值范围.