基于多目标优化的电力电缆排管敷设方法研究
王 剑 马 潇 刘 彬 金 欢 白 旭
(中国电力科学研究院)
0 引言
电力电缆排管是敷设地下电缆的重要方式,排管通道中包含多根管道,不同位置排管孔位散热性能不一样,将发热功率较大的电缆放置于散热性能较差的排管中,势必导致该回路电缆温度升高明显,影响其载流量[1,2],而将发热功率最高的电缆放置于散热最好的孔位将可有效增加线路载流量,因而有必要对排管敷设电缆进行优化,以提高线路经济效益[3-5]。
排管外部包覆有混凝土或砖墙,Carson等人[6]采用实验方法研究了电缆排管外覆层对电缆外部热阻的影响。为提高排管敷设电缆在短期内的载流能力,Sakata等人[7]对遗传算法进行改进,用以提高电缆电阻和载流量的计算精度。Moutassem[8]从标准IEC载流量计算公式[9-12]出发,研究了不均等负荷下排管敷设电力电缆优化策略,经过与CYMCAP软件计算结果对比显示,优化后的电缆载流量能够至少提高10%,但计算过程并未考虑各回路电缆之间的相互制约作用,所得结果不够准确。Davound分别从电流谐波效应[13]和电缆生命周期[14]角度提出了地下电缆合理布置方法,并应用到排管敷设中,提高了线路输送容量。
王有元等[15]对电缆载流量和温度场分布进行有限元分析,结合IEC60287方法计算土壤热阻和空气温度变化情况下的电缆载流量,对比验证了模型的有效性,并在此基础上分别研究了土壤热阻系数、环境温度、外部热源、电缆敷设方式、深层土壤温度对电缆载流量的影响。针对排管敷设电缆群暂态温度场和短时载流量,梁永春等人利用有限元法计算地下排管电缆温度场分布,并给出时间域内地下排管敷设的电缆温度变化过程和最终暂态温度场分布[16-18]。相关学者采用有IEC标准和有限元方法对多种敷设方式下的电缆载流量进行了一定的分析,但在排管优化敷设电缆分析方面的研究不足。
为更好地解决排管敷设电缆优化布置问题,本文研究了排管中电缆载流量计算分析方法,推导出排管中每一根电缆温升计算公式,以电缆温升最小为目标,构建子目标优化函数,并组合成为多目标优化函数,在典型3×4排管中敷设三回路电缆,按照电缆敷设孔位对敷设方案进行编码,以便计算机程序识别,采用NSGA-III算法分析问题pareto解,并以各根电缆温升方差最小为条件筛选出相对最合适的排管敷设方式,作为最优敷设方案,计算得到电缆载流量和温升。
1 电力电缆载流量分析
1.1 电力电缆热路模型
对电缆通以交流电,在传输电能的同时也会在导体上和金属护套上产生感应电流,在电阻的作用下形成热损耗,同时绝缘层在电压的作用下产生介质损耗,并以热量的形式散发出来,对周围环境具有加热作用。当电缆处于稳定运行状态时,电缆散热等于电缆内所有热损耗之和,敷设于排管中的电缆,热量通过热对流经过空气传导到排管内壁,同时有一部分热量通过热辐射由电缆外表面传递至排管内壁,传递到排管的热量再经过外部混凝土包封和土壤传递到大气中。为定量化地求解电缆的温升情况,Neher和McGrath根据A.E.Kennelly的假设提出了电力电缆热路模型,可以计算得到电缆的温升表达式,由电缆耐热限值进而可以得到电缆的最大输送电流,即载流量,其计算公式为:
(1)
式中,
Δθ为高于环境温度的导体温升,单位为开(K);
I为一根导体中流过的电流,单位为安培(A);
R为导体在最高工作温度下单位长度的交流电阻,单位为欧每米(Ω/m);
Wd为每相导体绝缘单位长度的介质损耗,单位为瓦每米(W/m);
T1为一根导体和金属套之间单位长度的热阻,单位为开米每瓦(K·m/W);
T2为金属套和铠装之间衬垫层单位长度的热阻,单位为开米每瓦(K·m/W);
T3为电缆外护套单位长度热阻,单位为开米每瓦(K·m/W);
T4为电缆表面和周围介质之间单位长度的热阻,单位为开米每瓦(K·m/W);
n为电缆中载有负荷的导体数(导体界面相同、负载相同);
λ1为电缆金属套损耗相对于该电缆所有导体总损耗的比率;
λ2为电缆铠装损耗相对于该电缆所有导体总损耗的比率。
1.2 排管敷设电力电缆载流量分析
排管中敷设多回路电缆时,由于多组电缆之间互相加热的作用,温升值Δθ会小于电缆芯最高温度和初始环境温度的差值,对电缆进行任意排序,取标号第1根电缆和第2根电缆进行分析,计算第2根电缆对第1根电缆加热所产生的温升Δθ21计算式可以表示为:
Δθ21=P2T12
(2)
其中:
P2为第二根电缆的发热功率;
T12为第一根电缆和第二根电缆之间的热阻。
第二根电缆的发热功率可以表示为:
(3)
其中:
n2为第2根电缆的芯数;
I2为第2根电缆的电流值;
R2为第2根电缆的交流电阻值;
λ12为第2根电缆的金属套损耗相对于该电缆所有导体总损耗的比率;
λ22为第2根电缆的铠装层损耗相对于该电缆所有导体总损耗的比率;
μ2为由日负荷因数计算得到的第2根电缆损耗因子,此处取为1;
Wd2为第2根电缆的绝缘介质损耗。
第1根电缆和第2根电缆之间热阻可以表示为:
(4)
代入式(2)可得温升计算式为:
(5)
敷设于排管中的第i根电缆对第1根电缆的加热作用可以表示为:
(i=2,3,…,n,i≠1)
(6)
综合各根电缆对第1根电缆的加热作用,可得电缆实际允许温升为:
Δθ=Δθ1-Δθ21-Δθ31-L…-Δθn1
(7)
代入至式(1)进行温度修正,可得第一根电缆的载流量计算公式为:
(8)
同理可得第i根电缆的载流量计算公式为:
(9)
可以表示为:
(10)
在排管中敷设的电缆其载流量均可采用上式进行计算。
2 电力电缆排管敷设多目标优化
2.1 电力电缆排管优化敷设目标函数
排管敷设电力电缆优化布置是分析最优的电缆布置方法使得各回路电缆的载流量均达到最大,即式(10)中的电流计算结果在所选布置方法下最大,由式(10)可见,电缆的载流量与其他电缆的电流存在函数关系,计算电缆组中第i根电缆到第n根电缆的最大值是一个隐函数的寻优问题。对隐函数进行寻优将使得问题复杂程度大幅提高,此处将该问题转化为显式函数进行分析。
考虑到电缆线路在设计时会结合用电负荷选择一定的电缆型号,在选定电缆设计容量时,根据线路电压信息可以确定电缆所要求的电缆输送电流设计值;同时考虑到电缆载流量的受控因素为温度,即问题可以转化为在一定电流下,合理布置电缆孔位以尽量降低各回路电缆的温度。当温度较低且低于温度上限时,电缆的电流还有进一步上升空间,即电缆线路具有更大的载流能力;反之在某一种敷设方式下有某回路电缆温度超限,则会降低电缆线路的载流容量。
由式(10)可得按一定次序排列的电缆组在一定电流作用下,第1根电缆的温升表达式为:
(11)
同理对于第i根电缆,温升表达式可以表示为:
(12)
式(12)即为优化问题的子目标函数,将子目标函数组合可得问题的总目标函数,如下所示。
(13)
其中:
dij=f(Ξ)
s.t.
其中:
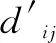
通过上述推导,电力电缆排管优化敷设问题转化为分析在既定的电缆输送容量下分析合适的敷设方式使得式(13)中每一根电缆温升最小,即对(13)式进行多目标优化。
2.2 采用NSGA-III优化目标函数
2.2.1NSGA-III算法
针对多目标优化问题,相关学者提出了很多解决方案,其中Deb教授于2014年在快速非支配排序遗传算法的基础上提出了一种新的多目标优化算法NSGA-III算法。该算法能够较好地求解多目标优化问题解[23]。
2.2.2采用多目标优化方法分析排管敷设电缆优化布置
采用多目标优化方法分析排管优化布置方法,首先设置迭代总数N,一般可取为1000;设置初始布置方案集,包括确定电缆排管的型号、电缆型号、初始布置方案等;其次计算各回路电缆电磁损耗,包括计算电缆直流电阻、电缆集肤效应因数、电缆邻近效应因数、电缆交流电阻、电缆金属套和屏蔽损耗因数以及电缆铠装层损耗因数;再者计算各回路电缆热阻,包括计算各电缆的绝缘热阻T1、金属套和铠装之间热阻T2、电缆外护层热阻T3、电缆外部热阻T4以及各电缆之间等效热阻Tij,其中电缆外部热阻T4采用有限元方法计算;而后计算在初始布置方案下每根电缆的温升值,利用NSGA-III方法优化求解得到下一代种群,迭代数加一,并比较是否达到预设迭代总数,未达到时利用新NSGA-III生成的下一代种群生成新的布置方案集,达到时则输出优化结果集,即电缆排管敷设优化布置方案。
具体计算过程如图1所示。
3 电力电缆排管优化敷设算例
3.1 排管参数
以《国家电网公司输变电工程通用设计》中典型3×4断面排管敷设电力电缆为例,研究在其中放置三回路单芯交流电缆的布置方式。
排管断面图如图2所示。
3.2 电力电缆参数
依据某小区用电需要,选用三种型号的电缆敷设于排管中,分别为:
1)YJLW02-64/110kV-1×800mm2铜芯交联聚乙烯绝缘皱纹铝护套聚氯乙烯外护套单芯电力电缆;
2)YJQ03-Z-64/110kV-1×500mm2铜芯交联聚乙烯绝缘合金铅护套聚乙烯外护套纵向阻水单芯电力电缆;
3)YJLW03-127/220kV-1×1000mm2铜芯交联聚乙烯绝缘皱纹铝护套聚乙烯外护套单芯电力电缆。
电缆电气计算参数如表1所示。
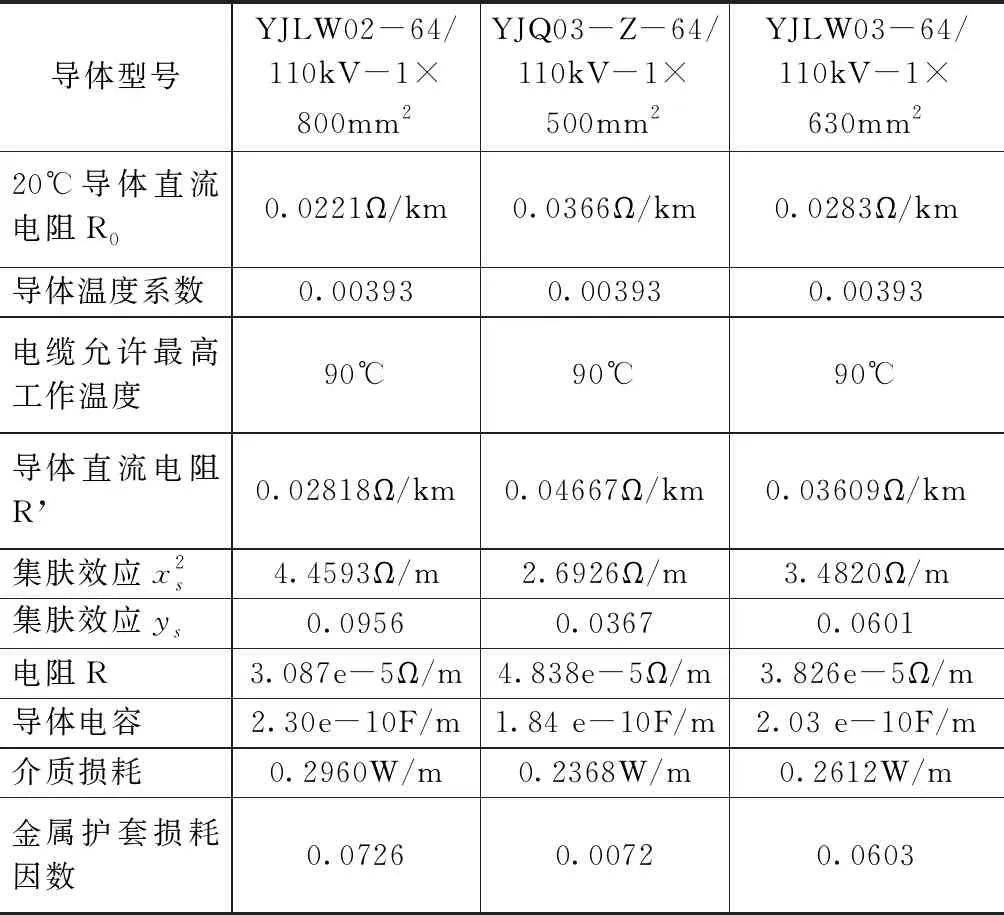
表1 电缆电气计算参数
根据电缆各层热阻计算公式计算得到热阻如表2所示。
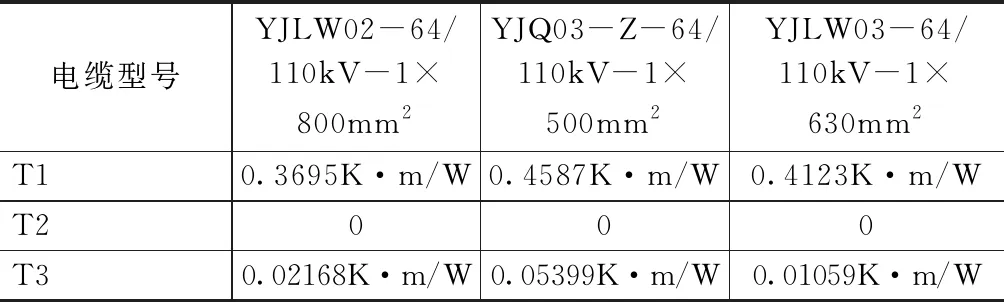
表2 电缆热阻计算
3.4 电力电缆排管敷设多目标优化
3.4.1电力电缆排管初始敷设
由有限元法计算电缆外部热阻结果可见,电缆排管组中靠近边缘位置处的孔位热阻小,散热性能较好,而处于排管组中间位置的孔位环境热阻大,散热性能较差。
电缆通电发热,热量来源主要包括电缆导线芯焦耳热、金属层与屏蔽层损耗、铠装层损耗以及绝缘介质损耗,第i根电缆的发热功率计算式可以表示为:
(15)
考虑到有多根电缆同时敷设在排管中,同时兼顾算例的普适性,设置三回路电缆的电流分别为:680A、530A和620A,以110kV电压供电,三回路电缆的供电容量分别为74.8MVA、58.3MVA和68.6MVA。计算得到三回路电缆的发热功率如表3所示。

表3 电缆发热功率
进行初始化布置时,将发热功率较大的布置于散热性能较好的孔位,将发热功率较小的电缆布置于散热性能较差的孔位。结合电缆发热功率和排管孔位散热性能,将三回路电缆敷设于排管组中,初始布置方式为:
3.4.3排管敷设电缆优化计算
采用NSGA-III方法对电力电缆排管敷设布置方法进行寻优求解,以初始布置方式为起始,三回路9根电缆的温升为目标函数,设定初始种群规模为9×10=90,复制初始布置方式90组,进入计算程序,迭代1000代,得到一组最优布置解集,为问题的pareto解,各解均处于前沿面上。
可得每一组解对应的电缆布置方式。五种敷设方式下,从第一回A相电缆到第三回C相电缆依次序温升值如表4所示:

表4 各根电缆温升值(℃)
表4仅节选了前五组解显示出来,优化求解得到的解有90组,实际布置电缆时只能应用一种方案,因此需要采用筛选策略挑选出相对最合适的布置方案进行布置。由表4可见,方式3中最低温升为第二回路A相电缆,55.7℃,最高温升为第一回路A相电缆,69.8℃。该种敷设方式虽然使得第二回路A相电缆取得了相对较低的温升,但是以第一回路电缆温度高为代价的,综合考虑可不采取该解。此处选用温升值相对均衡的布置方式作为布置方案,即选择波动小者为最终解,考虑到方差能够表示数列的波动幅度,求解各组解所得温升的方差,输出温升方差最小所对应的布置方案。
计算各组敷设方式对应电缆温升方差,如图4所示。
筛选出温升方差最小的布置方案,对应的布置方案如图5所示。
图5中数字1、2、3分别表示第一、二、三回路电缆,同一回路使用的电缆型号一致,仅存在电流相位角度差,每一根电缆的ABC标志用以依次序区分电缆的相位,为从排管左上角到右下角以此标识,并不具备具体的相位意义,具体换位在实际施工时进行调整。
图5布置方案对应的各根电缆温升值如表5所示。

表5 优选布置方案对应的各电缆温升
由表5可见,各电缆温升相对均衡,布置效果较好。
5 结束语
研究了电缆排管敷设下电缆载流量的影响因素,分析得出了排管中敷设电缆载流量的计算公式,该计算式计算为隐式优化问题,考虑影响电缆载流量的制约因素为温度,将求取电流最大转化为求取电缆温升最小,进而将问题转化为方便求解的显示问题。结合NSGA-III多目标优化算法与方差筛选法,分析得到排管敷设电缆最佳敷设方式,相比于初始布置方式,优化后的排管敷设电缆可有效提升输送容量。本文研究成果可以有效用于指导排管电缆敷设方法,提升排管使用经济效益。

