高中数学存在性问题常见题型及解题策略

山东 史立霞 秦 振

高中数学存在性问题，一般是已知某些条件，判断是否存在某种数学对象，使结论成立.这类问题的解题策略是先假设符合条件的数学对象存在，然后进行运算和推理，若经过运算能求出这个数学对象，或经过推理没有产生矛盾，那就说明符合条件的数学对象存在；若经过运算求不出这个数学对象，或者经过推理产生矛盾，那就说明符合条件的数学对象不存在.也可以找出一个符合条件的数学对象，然后证明其存在.下面结合例题介绍高中数学存在性问题的常见题型及解题策略.

一、是否存在“值”的问题

题型特点：一般是在确定的条件下判断某个常数是否存在，或是否存在某个常数的范围，或某条线段是否存在最小值(或最大值)，或某个图形的面积是否存在最小值(或最大值)的问题.这类问题常常出现“是否存在”“是否有”“是否变化”等疑问词，以示结论有待判断.

解题策略：解决这类问题的策略是先假设需要探索的“值”存在，从条件和假设出发进行运算、推理，若出现矛盾，则否定存在；若不出现矛盾，则肯定存在.

【例1】(2019·全国卷Ⅲ理·20)已知函数f(x)=2x3-ax2+b.

(Ⅰ)讨论f(x)的单调性；

(Ⅱ)是否存在a，b，使得f(x)在区间[0,1]的最小值为-1且最大值为1？若存在，求出a，b的所有值；若不存在，说明理由.

【分析】(Ⅰ)求出f′(x)，利用导数与单调性的关系讨论解决；(Ⅱ)假设满足题设的a，b存在.由(Ⅰ)的结果，将问题转化为单调区间上的函数值问题，根据题意列出方程组，解方程组，得到a，b的值，然后判断所得值是否满足条件，得出结论.

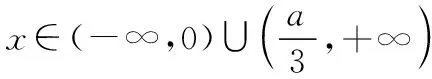
若a=0，f(x)在(-∞,+∞)上单调递增.

(Ⅱ)设满足题设的a，b存在.

(ⅰ)当a≤0时，由(Ⅰ)知，f(x)在[0,1]上单调递增，所以f(x)在[0,1]上的最小值为f(0)=b，最大值为f(1)=2-a+b.此时a，b满足题设条件当且仅当b=-1，2-a+b=1时，即a=0，b=-1.

(ⅱ)当a≥3时，由(Ⅰ)知，f(x)在[0,1]上单调递减，所以f(x)在[0,1]上的最大值为f(0)=b，最小值f(1)=2-a+b.此时a，b满足题设条件当且仅当b=1，2-a+b=-1时，即a=4，b=1.

综上，当且仅当a=0，b=-1或a=4，b=1时，满足f(x)在[0,1]上的最小值为-1，最大值为1.

【说明】第(Ⅱ)问的解法具有代表性，它是利用(Ⅰ)的结果和方法，也就是由(Ⅰ)得到的“形成性解法”，经过计算，推理得到答案.

二、是否存在某种位置关系

题型特点：一般是在确定的条件下判断某一位置关系是否存在的问题.这类问题也是以“是否存在”“是否有”“是否变化”“能否出现”等疑问词呈现，以示结论有待判断.

解题策略：解决这类问题的策略是先假设需要探索的位置关系存在，设出点的坐标、或者直线方程、或者向量，从条件和假设出发进行运算、推理，若出现矛盾，则否定存在；若不出现矛盾，则肯定存在，最后求出点的坐标.

【例2】(2017·全国卷Ⅲ文·20)在直角坐标系xOy中，曲线y=x2+mx-2与x轴交于A，B两点，点C的坐标为(0,1).当m变化时，解答下列问题：

(Ⅰ)能否出现AC⊥BC的情况？说明理由.

(Ⅱ)证明过A，B，C三点的圆在y轴上截得的弦长为定值.

【分析】(Ⅰ)假设能出现AC⊥BC.设A(x1,0)，B(x2,0)，由x1，x2的特点，可得x1·x2=-2，验证直线AC的斜率与直线BC的斜率之积是否等于-1，即可得出结论.(Ⅱ)通过求BC，AB的中垂线的交点坐标来确定圆心坐标及半径.由弦心距、半弦长、半径组成一个直角三角形，借助勾股定理求出弦长为定值，从而得证.

【解析】(Ⅰ)不能出现AC⊥BC的情况.理由如下：

【说明】常见的位置关系还有点与点、点与线、线与线、点与二次曲线、直线与二次曲线、二次曲线与二次曲线的关系等，解题时通过数形结合，合理转化，将题目变为我们熟悉的“常规”问题来解决.

三、是否存在点的问题

题型特点：一般是在确定的条件下判断某一点，或某几个点是否存在的问题.这类问题也是以“是否存在”“是否有”“是否变化”等疑问词呈现，以示结论有待判断.

解题策略：解决这类问题的策略是先假设需要探索的点存在，设出点的坐标，从条件和假设出发进行运算、推理，若出现矛盾，则否定存在；若不出现矛盾，则肯定存在.最后求出点的坐标.

【例3】(2019·全国卷Ⅰ文·21)已知点A，B关于坐标原点O对称，|AB|=4，⊙M过点A，B且与直线x+2=0相切.

(Ⅰ)若A在直线x+y=0上，求⊙M的半径；

(Ⅱ)是否存在定点P，使得当A运动时，|MA|-|MP|为定值？并说明理由.

(Ⅱ)存在定点P(1,0)，使得|MA|-|MP|为定值.

理由如下：

【说明】第(Ⅱ)问的解法是从条件入手，根据问题的特点，借助图形的性质，数形结合，推出结果，是典型的综合法.这也是解存在性问题的常用方法.

四、是否存在直线的问题

题型特点：一般是在确定的条件下判断某一条直线，或几条直线是否存在的问题.这类问题也是以“是否存在”“是否有”“是否变化”等疑问词呈现，以示结论有待判断.

解题策略：解决这类问题的策略是先假设需要探索的直线存在，设出直线方程为y=kx+b，从条件和假设出发进行运算、推理，将问题转化为探索参数k和b的存在问题.若直线的斜率和截距存在，则所求直线存在，可求出直线方程；若出现矛盾，则否定存在.注意直线斜率不存在时，需要验证此时直线的存在性.

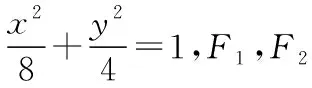
(Ⅱ)当∠F1AB=90°时，A在x轴上方，求A，B的坐标；

(Ⅲ)若直线AF1交y轴于M，直线BF1交y轴于N，问是否存在直线l，使得S△F1AB=S△F1MN，若存在，求出直线l的方程；若不存在，请说明理由.

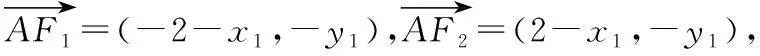
【说明】解第(Ⅲ)问时，根据直线的特点，设直线AB方程为x=my+2，避免了斜率的讨论；因可构成△F1AB，由m的存在判定直线l存在.在利用S△F1AB=S△F1MN时，根据图形的特征得S△F1AB=S△F1AF2+S△F1BF2，将两点M(0,ym)，N(0,yn)的坐标转化为用A(x1,y1)，B(x2,y2)的坐标表示，由此联想到根与系数的关系，得到关于m的方程，从而得到直线方程.从解题过程可知，解决问题的过程就是将问题合理转化的过程.

五、是否存在圆锥曲线的问题

题型特点：一般是在确定的条件下判断某条圆锥曲线是否存在的问题.这类问题也是以“是否存在”“是否有”“是否变化”等疑问词呈现，以示结论有待判断.

解题策略：解决这类问题的策略是先假设需要探索的曲线存在，设出曲线方程，从条件和假设出发进行运算、推理，若曲线是椭圆或双曲线时，就将问题转化为探索参数a，b的存在问题；若曲线是抛物线时，就将问题转化为求参数p是否存在问题；若曲线是圆时，设出圆的方程为(x-a)2+(y-b)2=r2，从条件和假设出发进行运算、推理，将问题转化为探索参数a，b和r的存在问题.若参数存在，则所求曲线存在，可求出曲线方程；若出现矛盾，则否定存在.

(Ⅰ)求双曲线E的离心率；

(Ⅱ)如图，O为坐标原点，动直线l分别交直线l1，l2于A，B两点(A，B分别在第一、四象限)，且△OAB的面积恒为8.试探究：是否存在总与直线l有且只有一个公共点的双曲线E？若存在，求出双曲线E的方程；若不存在，请说明理由.

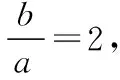
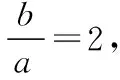
若直线AB与双曲线E另有公共点N，则x1≠x2.因为x1=x2时，A，B关于x轴对称，y0=0.从而由对称性可知，AB与双曲线E有两个公共点，相矛盾.

当x1=x2时，有x1=x2=2，点M(2,0)在E上，此时M为E的右顶点，为AB与E的唯一公共点.