基于死区补偿的空间机械臂积分变结构模糊控制

黄小琴

(闽江学院物理与电子信息工程学院，福建 福州 350108)

0 引 言

随着人类对太空领域探索的持续投入，空间机械臂作为航天领域的关键技术之一，成为航天活动越来越不可或缺的工具，因此对其各方面的研究受到诸多关注[1-5]。基座位姿均不受控时，空间机械臂系统为经典的非完整动力学系统，相较地面机械臂，相关建模与高精度运动控制的问题更为复杂。Gu Y L等利用增广变量理论，解决了基座位姿不控系统的运动控制问题[6]。

在空间机械臂执行机构中，实际存有诸如死区、饱和等多种非线性约束的情况。其中，关节输入力矩死区是主要的影响空间机械臂高精度控制的因素之一，且其是时变未知的，而以往对空间机械臂的运动控制研究中甚少考虑其影响，若不加以考虑，会造成控制精度的降低，因此有必要对其深入探索。张文辉等利用神经网络的逼近特性补偿了死区，保证了空间机械臂的高精度控制[7]。胡庆雷等考虑执行机构存在的死区特性，设计了空间机器人终端滑模自适应补偿跟踪控制器[8]。Seong I H等将死区因素视为不确定性，设计一个滑模面控制策略，以调整增益参数来实现控制死区的影响[9]。本文结合前述的文献研究，以考虑未知死区的空间机械臂系统为研究对象，建立其动力学方程。采用线性化的死区模型，设计具有积分形式的切换函数来减少外部扰动引起的稳态误差。利用模糊逻辑函数的近似特性，在此基础上，借助增广变量法，提出了一种积分变结构自适应模糊的控制器。最后，通过Lyapunov函数证明控制方法的稳定性，以Matlab仿真验证其有效性。

1 系统动力学建模

本文考虑系统构型如图1所示的两杆空间机械臂系统，在X-Y平面运动。若忽略微重力，则系统无其他外力作用，此系统遵循动量守恒定律。根据Lagrange第二类方程，可推出基座位置、姿态均不受控的欠驱动形式的系统动力学方程：

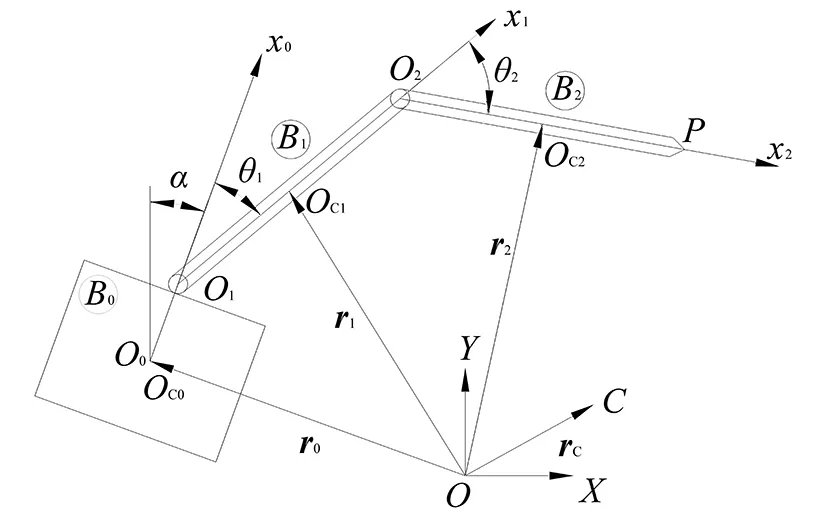
图1 漂浮基两杆空间机械臂系统

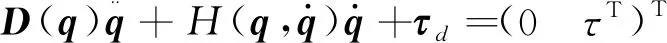
(1)

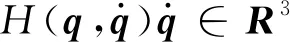
2 死区模型

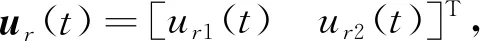
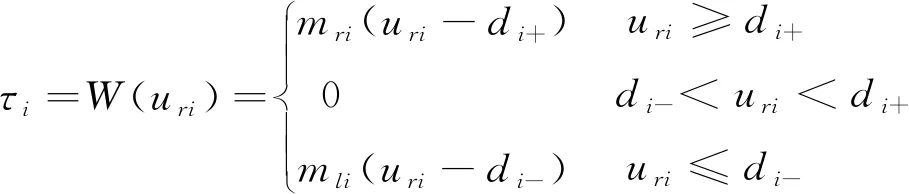
(2)

其中，i=1,2表示机械臂的第i个关节；di-和di+分别为死区的左右断点；mli和mri分别为死区的左右斜率。假定死区的斜率在正负区域是相同的，即mri=mli=mzi。di-、di+、mzi是未知不确定的，但它们有界的且符号已知，di+>0，di-<0和mzi>0。

把死区模型写成以下形式：

τi=W(uri)=mziuri+cri(uri)

(3)

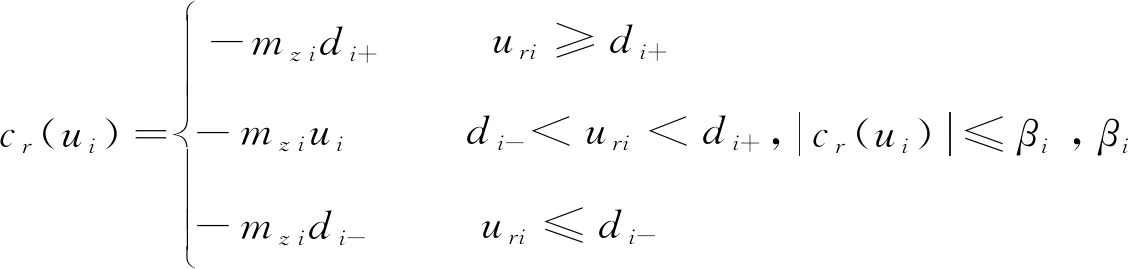
3 空间机械臂增广模糊自适应控制器设计

3.1 模糊逻辑系统及其函数逼近

包含单点模糊化、乘积推理以及中心平均加权去模糊化的模糊系统输出f(x)为[12-13]:

f(x)=UTχ(x)

(4)

其中，U是权值矩阵，χ(x)=[χ1,…,χl]T为模糊基向量，l为模糊系统的规则数目。模糊基函数χk可表示为：

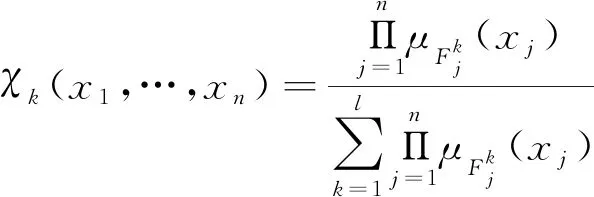
(5)

其中，输入x=[x1,x2,…,xn]T∈Ωx⊂Rn，Ωx为有界的闭区域。

3.2 增广模糊自适应控制器设计

定义具有积分的增广切换函数

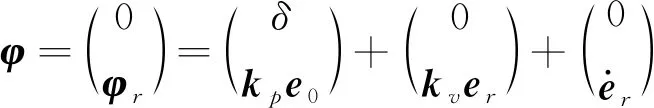
(6)

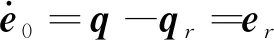
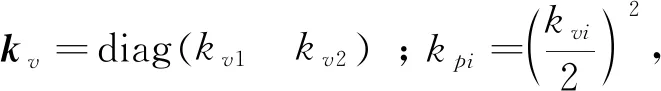
将式(6)两边对时间t求导，

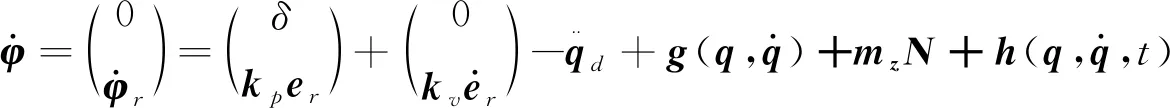
(7)

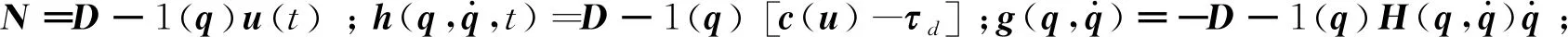
对Yφ(t)关于时间t求导把式(7)代入可得：

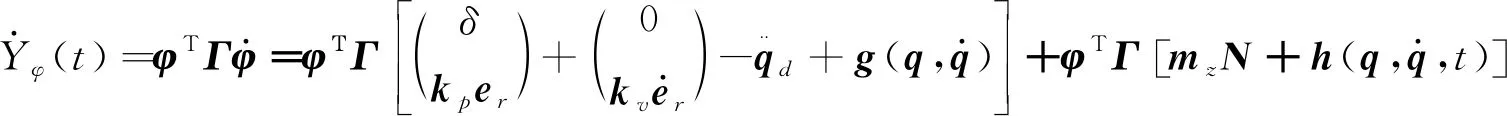
(8)

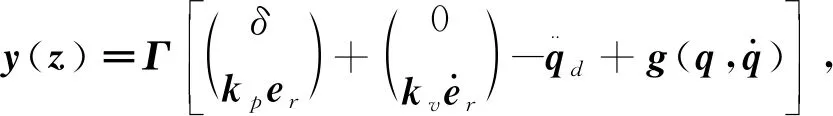
用模糊逻辑函数来近似y(z)，设y(z|U)为y(z)的一个逼近，即

y(z|U)=UTχ(z)

(9)

U的最优值U*是一个常数矩阵并满足

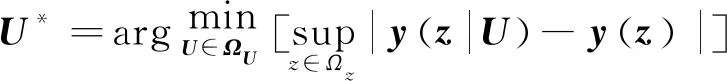
(10)

其中，ΩU={U|‖U‖≤MU},有界正常数MU是设计参数。

y(z)=U*Tχ(z)+ε

(11)

其中，ε为逼近误差，|ε|≤εy。

由式(9)～式(11)，可得

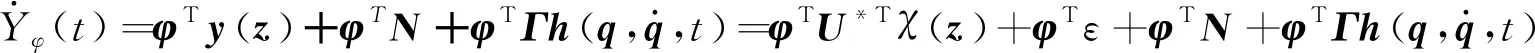
(12)

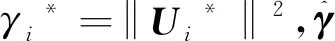
(13)

其中，β>0是设计常数。

将式(13)代入式(12)可得

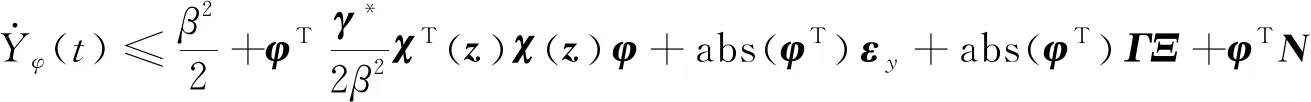
(14)

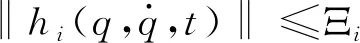
采用如下控制律

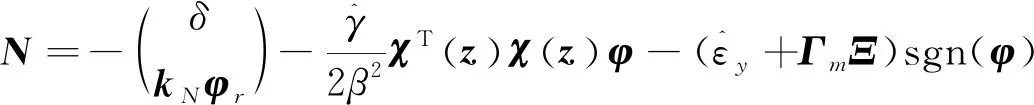
(15)

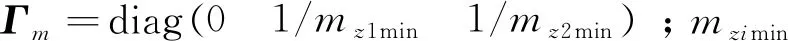
最终可得系统最终增广控制律为：

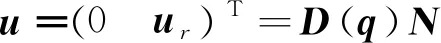
(16)

定理对于式(1)所示的系统动力学方程，若初始条件满足有界性，采用式(15)、式(16)的控制规律以及如下自适应调节规律

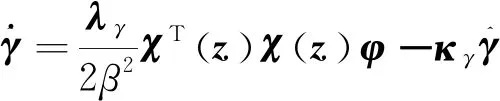
(17)

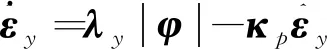
(18)

证明构造Lyapunov函数为

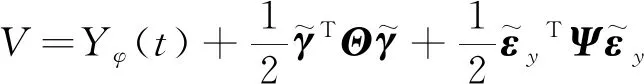
(19)

将V对时间求导，得

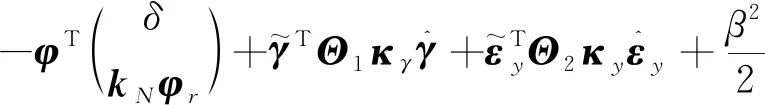
(20)

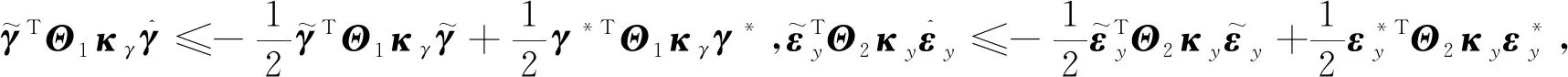
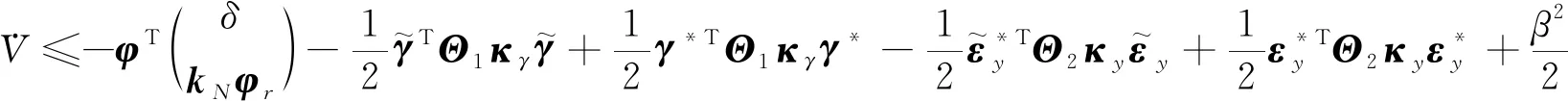
(21)

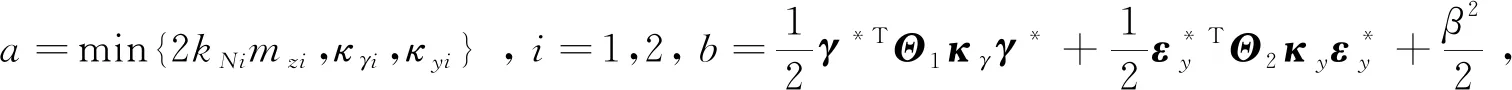
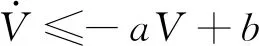
(22)

两边同乘以eat得

(Veat)′≤beat

(23)

不等式两边求[0，t]的积分，可得

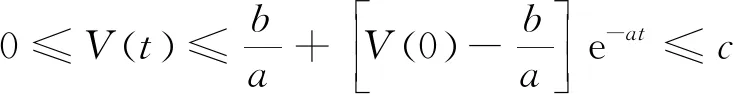
(24)

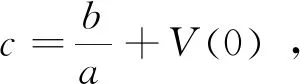
(25)

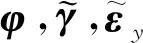
4 仿真验证

将图1所示的系统作为仿真验算实例，选取参数：l0=1.5 m，l1=l2=1 m，a1=a2=0.5 m；各分体质量为：m0=40 kg，m1=2 kg，m2=1 kg；中心惯量矩：J0=34.17 kg·m2，J1=J2=1.5 kg·m2。应用Matlab进行仿真。

臂杆两关节的期望运动轨迹为:θ1d=(π/3)-1+cos(πt/3)，θ2d=sin(πt/3)+(π/3)。

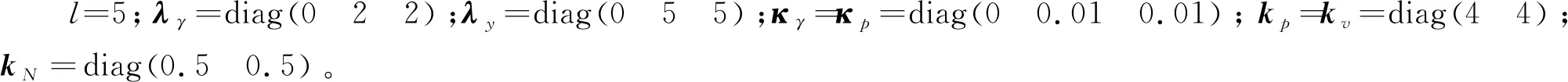
选取隶属度函数为通用的高斯型函数:

死区参数：d1-=d2-=-10；d1+=d2+=10；mz1=mz2=1；mz1min=mz2min=0.85

图2为仿真为开启死区补偿控制时，载体的实际轨迹图，可以看出，虽然载体位置和姿态不受控制，但运行平稳。图3为此条件下系统臂杆两关节qr与qrd轨迹跟踪图，图4为相应的跟踪误差er。图5仿真为关闭死区补偿控制时，臂杆两关节的轨迹变化图。对比可以看出，存在未知死区和外部干扰的情况下，如果不对死区进行补偿，两关节无法跟踪期望轨迹，而本文所采用的控制器可有效地控制系统臂杆两关节协调地完成期望运动。

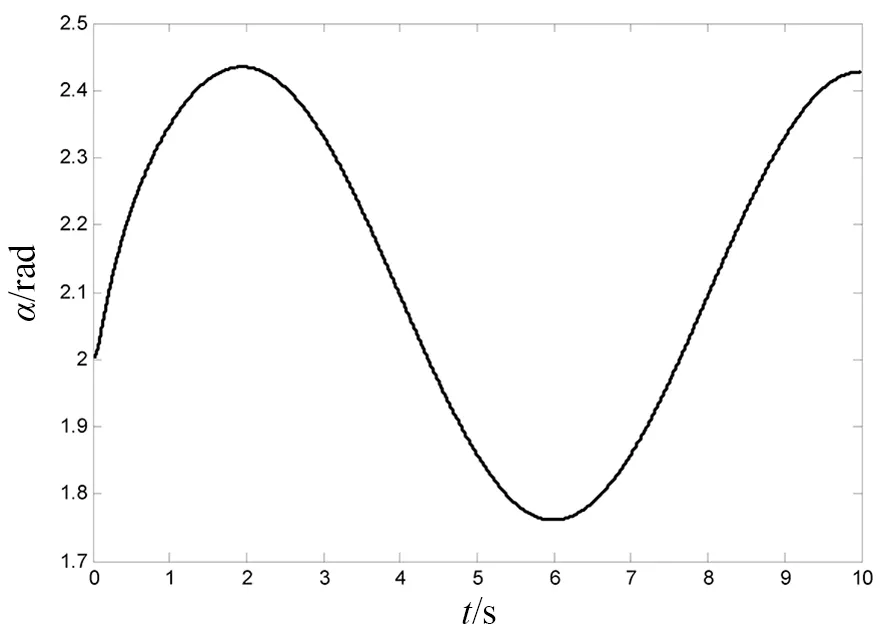
图2 载体的实际轨迹

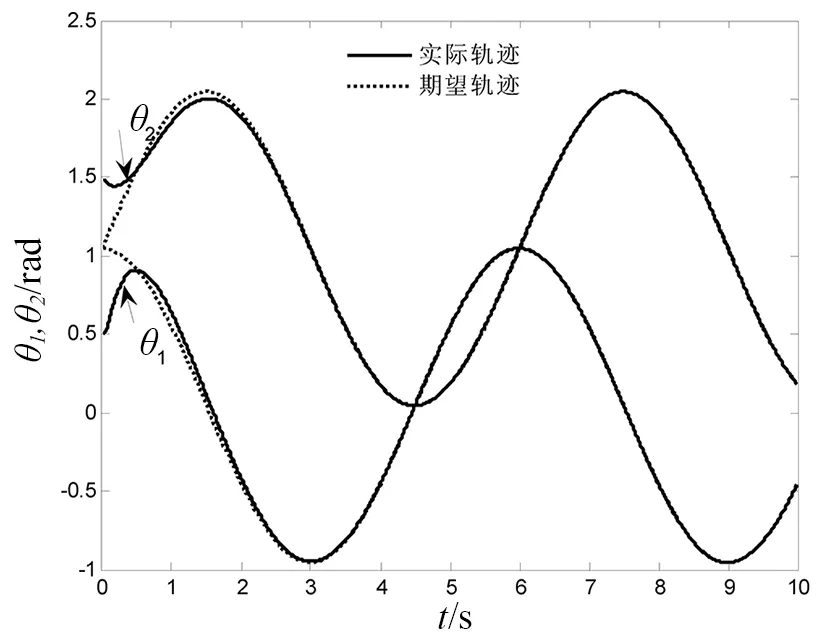
图3 臂杆两关节的轨迹跟踪

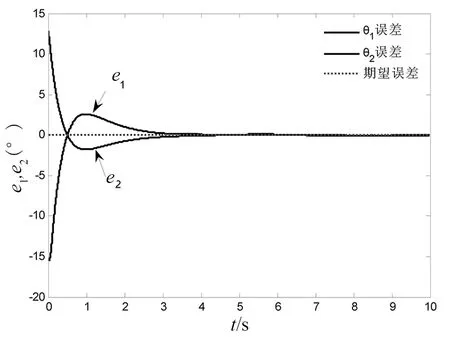
图4 臂杆两关节的跟踪误差

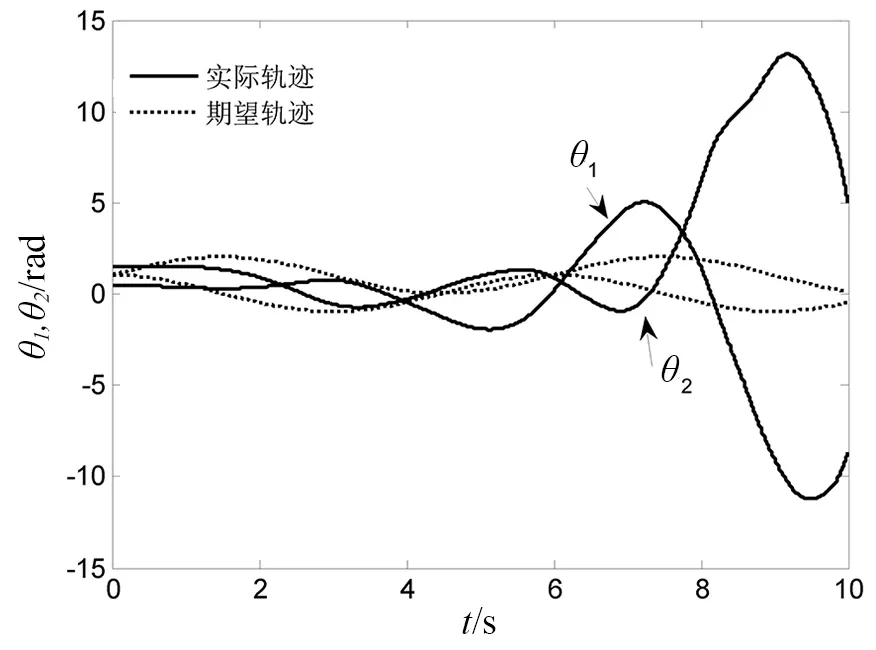
图5 臂杆两关节的轨迹跟踪(关闭死区补偿器)

5 结论

本文针对受到外部干扰和未知死区特性的空间机械臂系统，提出了一种可积分变结构模糊自适应控制方案，该方法可以克服死区的影响，设计的积分型切换函数可减少系统的外部扰动和稳态误差。Lyapunov函数的稳定性分析证明了该算法可确保闭环系统是半全局一致终结有界的。仿真运算证实了臂杆两关节能跟踪上刚性的期望运动轨迹。