能量法预测316L不锈钢蠕变疲劳交互作用寿命

陈健飞 黄保科 解学方 蒋文春 王振波 李圣军 张玉福 苏厚德 裴二阳

（1.中国石油大学（华东）新能源学院；2.中国石油化工股份有限公司胜利油田分公司技术检测中心；3.桐昆集团股份有限公司；4.甘肃蓝科石化高新装备股份有限公司；5.中国机械工业联合会）

随着现代工业向高温、高压及高速等高参数方向发展，在石油化工、核能电力及航空航天等领域越来越多的设备长期在高温、高压及交变载荷等复杂工况下运行，此类设备的服役往往受疲劳、蠕变及腐蚀等多种因素的制约［1］。尤其是化工行业的高温承压设备，不仅承受设备本身工作的应力， 而且承受高温致使的蠕变损伤与调峰、运停及温度波动等致使的疲劳损伤，蠕变疲劳交互作用是此类设备失效的重要因素［2］。 疲劳载荷在高应力区产生塑性变形， 导致晶体内部产生位错、滑移等缺陷，从而产生穿晶的疲劳微裂纹。 蠕变使晶体在晶界处形成空穴，随着时间的积累产生沿晶裂纹。 高温下的循环载荷，疲劳穿晶裂纹与蠕变沿晶裂纹于晶间相遇，蠕变孔洞可以作为疲劳源促进疲劳裂纹的萌生和扩展，疲劳循环也可以加速蠕变孔洞的成核和长大，两者间相互作用、相互促进，形成蠕变与疲劳间的交互作用［3，4］。

蠕变疲劳交互作用寿命预测方法多是基于准确的损伤评估， 根据损伤交互图确定交互寿命，例如线性累积损伤法、连续损伤力学法等，其中时间数分法和延性耗竭法被广泛应力于工程中。 由经验得出的交互图显然是种假设，理论依据不强，且此类规范包含较大的安全系数，偏于保守，远低于最优化的设计准则，可能会导致过度设计或者不可实现设计［5］。 笔者采用能量法预测蠕变疲劳交互作用寿命，并提出了一种新的滞回能密度计算方法，在经典疲劳寿命与滞回能幂率关系的基础上，添加蠕变和交互的时间影响因子，根据蠕变疲劳交互试验半寿命周期稳定的磁滞回线确定参量，拟合了寿命预测公式，该公式对参量的变化很敏感，能准确预测蠕变疲劳交互作用寿命。

1 基于能量法的疲劳寿命模型

金属材料的疲劳是指在应力或者应变循环载荷的反复作用下引起损伤的过程［6］。 进行恒定应变幅的对称循环疲劳试验， 加载波形如图1所示，可以得到应力与应变之间的加载过程（图2），称为磁滞回线。 部分金属材料（例如316L不锈钢）会出现随着循环次数N的增多， 应力幅逐渐增大的循环硬化现象，在循环次数达到几十次后即可形成稳态磁滞回线，一般取半寿命周期为稳定的磁滞回线［7］。

图1 疲劳加载波形

图2 循环应力应变曲线

不同应变幅的对称循环疲劳试验数据可以获得一系列的半寿命周期稳态的磁滞回线，在同一坐标系中将稳态磁滞回线的循环应力幅Δσ和应变幅Δεt连线后可以得到如图3所示的循环曲线，图中σa、εa分别是当前循环的峰值应力、峰值应变。

图3 循环应力幅与应变幅关系曲线

应变幅与循环应力幅之间的关系遵循Ramberg-Osgood方程［8］：

式中 E——弹性模量；

K′——循环硬化系数；

n′——循环硬化指数；

Δεe——弹性应变幅；

Δεp——塑性应变幅。

循环应力幅与塑性应变幅间的幂率关系为：

由试验数据可以得到疲劳半寿命周期稳定的磁滞回线， 从而可知循环应力幅与塑性应变幅，进行对数回归分析后可以得到循环硬化系数K′与循环硬化指数n′。

大量疲劳试验结果表明［8，9］滞回能密度w与疲劳寿命Nf间存在幂率关系，即：

式中 β0、C0——取决于材料和温度的参数。

2 基于能量法的蠕变疲劳交互作用寿命模型

2.1 蠕变疲劳交互作用寿命预测方程修正

当保载时间th=0时，式（4）即为式（3）所示的疲劳寿命公式。 当保载时间足够大时，蠕变疲劳交互作用寿命可视为Ncf=1，式（4）可以看作蠕变寿命计算式［11］，转化为蠕变断裂时间与能量间的关系：

式中 tr——蠕变断裂时间；

W——机械功。

2.2 蠕变疲劳交互滞回能密度计算

试验或模拟得到图3所示稳定的磁滞回线的面积即为滞回能密度，疲劳的滞回能密度已有较为成熟的计算公式［9，12］：

蠕变疲劳交互的加载波形如图4所示为梯形波，在最大应变处保载一段时间。 相对于纯疲劳的稳定磁滞回线， 在应力峰值处由于蠕变的存在，会产生应力松弛得到蠕变疲劳交互半寿命周期稳定的磁滞回线（ABCEFA）如图5所示。

图4 蠕变疲劳交互加载波形

图5 蠕变疲劳交互磁滞回线

笔者提出一种计算滞回能密度的方法，蠕变疲劳交互半寿命周期稳定磁滞回线的面积可视为纯疲劳磁滞回线面积SABCDEF减松弛应力所在三角形面积SCDE，即：

由于C、D两点的应力值差别极小， 可以忽略不计，将SCDE视为直角三角形，其面积为：

由纯疲劳滞回能密度计算公式可以得到SABCDEF为：

结合式（7）～（9）可得出蠕变疲劳交互半寿命周期稳定的滞回能密度为：

式中 Δεp，BF——BF间的塑性应变；

σrelax——蠕变松弛应力。

3 结果与讨论

3.1 循环硬化指数的确定

316L不锈钢在600℃加载图1所示波形的疲劳试验［13］，控制应变幅分别为0.4%、0.5%、0.6%、0.7%、0.8%， 由半寿命周期稳定的疲劳磁滞回线获得的塑性应变幅与应力幅见表1。

表1 疲劳试验特征参量

采用表1所示数据用Origin拟合式（2），结果如图6所示， 可得应力幅与塑性应变幅间的幂率关系为：

图6 应力幅与塑性应变幅关系拟合

3.2 蠕变疲劳交互作用寿命预测

316L不锈钢在600℃下进行蠕变疲劳交互试验［13］，加载波形如图4所示，控制应变幅为0.7%，保载时间分别为0（即疲劳试验）、1、5、10、30min，由蠕变疲劳交互半寿命周期稳定的磁滞回线可知其应力幅、 图5所示BF间的塑性应变和蠕变致使的应力松弛量（表2）。 由式（2）、（11）可得n′=0.27，结合以上数据根据式（10）计算，可得出不同保载时间的蠕变疲劳交互半寿命周期稳定的滞回能密度（表2）。

在双对数坐标系中滞回能密度与疲劳、蠕变疲劳交互作用寿命呈线性关系（图7），根据疲劳和蠕变疲劳交互试验数据［13］得到循环次数和滞回能密度，使用软件auto2fit5.5拟合式（4）可得：

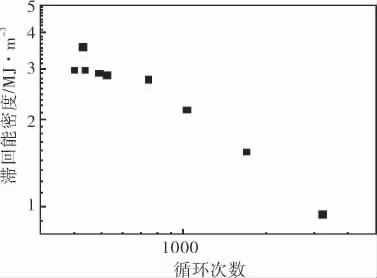
图7 滞回能密度与蠕变疲劳交互寿命关系拟合

根据试验数据拟合得到的蠕变疲劳交互作用寿命计算式，配置控制应变幅为0.7%，保载时间分别为0、1、5、10、30min， 根据试验条件进行有限元计算，结合笔者提出的式（10）所示的新的滞回能密度计算方法，得到不同保载时间的滞回能密度，代入蠕变疲劳交互作用寿命计算公式（12）即可计算得出不同保载时间的蠕变疲劳交互作用寿命。衡量有限元模拟计算得出的蠕变疲劳交互作用寿命的准确性，可以用寿命预测因子LPF表示：

不同保载时间的蠕变疲劳交互作用寿命数值模拟值与试验值的对比如图8所示。 由图可以看出通过文中的能量法，配置不同保载时间与试验相同条件的有限元模拟，蠕变疲劳交互作用寿命预测结果LPF<1.15，准确程度较高。 而且此能量法对参量变化的敏感程度较高，易于计算节省成本的同时，保证了蠕变疲劳交互作用寿命预测的准确性，为材料的高温设计提供了理论依据。

图8 模拟计算寿命准确性检测图

4 结论

4.1 基于经典疲劳理论和600℃下不同应变的316L不锈钢纯疲劳试验，研究应力幅与塑性应变幅之间的幂率关系，确定了循环硬化指数n′。

4.4 配置相同条件的蠕变疲劳交互模拟，根据文中提出的滞回能计算方法和拟合出的寿命计算公式计算出寿命， 与试验相比， 寿命预测因子LPF＜1.15。