音圈快速反射镜的完全跟踪控制

王福超，王昱棠*，田大鹏

(1.中国科学院 航空光学成像与测量重点实验室，吉林 长春 130033；2.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)

1 引 言

航空、航天成像装备及其他高端光电仪器对成像距离提出了更高的要求，而随着探测距离的不断提升，成像设备的稳定精度要求也越来越高。传统控制视轴指向的机械框架惯量大、刚度低，并且受到设计约束和干扰力矩等因素的影响，系统控制精度以及控制带宽难以提升。快速反射镜(Fast Steering Mirror，FSM)具有体积小、质量轻、结构紧凑、响应快、精度高等优点[1-2]，广泛应用于空间光通信、像移补偿以及高精度跟踪瞄准等领域[3-5]。通过在成像光路中加入FSM并采用复合轴控制方式补偿视轴晃动，有效提高了视轴稳定精度和系统的成像质量[6-9]。

FSM按照驱动方式不同主要分为压电陶瓷驱动和音圈电机驱动[10]。压电陶瓷驱动方式具有力矩输出大、响应带宽高的优点，但这种驱动方式下FSM的行程较小，并且驱动电路相对复杂。同时，压电陶瓷存在迟滞、蠕变等非线性特性，需要通过算法进行补偿，增加了工程应用的复杂度。与之相比，基于音圈电机驱动的FSM(以下简称音圈FSM)具有行程大、动态特性好、结构简单、环境适应性强等特点，工程应用更为广泛。

国内外相关机构已设计并制造多种音圈FSM。美国Ball Aerospace公司设计的多尺寸音圈FSM行程可达±50 mrad，工作带宽可达250～1 000 Hz。美国OIM公司生产的音圈FSM角度为±27 mrad，工作带宽大于500 Hz。国内对于音圈FSM的研制起步较晚，但发展较快。国防科技大学设计的音圈FSM的转动范围为±5 mrad，闭环控制带宽为360 Hz[11]，长春光机所研制的一种音圈FSM的工作带宽为213 Hz[12]。但是，上述带宽指标均只考虑幅值下降，而未对相位滞后进行衡量。实际上，相位滞后会直接影响FSM的实际应用效果。在音圈FSM补偿系统视轴稳定时，较大的相位滞后会导致反射镜的实际运动与指令之间偏差的绝对值较大，直接影响系统视轴稳定精度。随着光学系统口径、焦距的提高，这一问题也愈发凸显，如何在保证音圈快速反射镜工作带宽的前提下减少系统的相位滞后，已成为提升音圈FSM性能的关键问题之一。

实际工程中采用的FSM控制方法仍然以传统的PID控制以及超前滞后校正方法为主。然而，传统控制方法不仅鲁棒性较差，其闭环系统存在明显的相位滞后现象。为了解决上述问题，文献[13]提出了一种基于零相差轨迹控制(Zero Phase Error Tracking Controller，ZPETC)的音圈FSM控制方法，提高了系统的响应速度。但是，该方法需要获取指令超前信息，并且为了避免不稳定零极点对消需采用近似逆模型，因此限制了系统频带的拓宽，理论上存在跟踪的幅值误差。

实际上，为了保证FSM的控制性能，其控制器的控制周期较短，而外部控制计算机发送给FSM控制器的指令周期往往大于反射镜的控制周期，即实际音圈FSM系统存在多速率采样问题。常见的思路是通过插补的方式解决控制周期与指令周期不同的多速率采样问题，但这样不能很好地利用这种采样速率的差异特性。文献[14]利用多速率采样特性，不对指令进行插补，通过对前馈的巧妙设计从理论上实现了控制系统对指令的完全跟踪控制(Perfect Tracking Controller，PTC)，其核心思想是把单输入单输出(Single Input Single Output，SISO)的被控对象描述为多输入多输出(Multiple-Input-Multiple-Output，MIMO)系统，从而构造出对象状态到输入控制量之间非奇异的传递函数矩阵。利用该模型求解稳定的逆控制即可实现高动态跟踪控制，在硬盘驱动器、单相逆变器等领域得到较广泛的应用[15-16]。国内对该方法的研究成果较少[17-18]。近年来，基于完全跟踪的光电跟踪转台控制及光刻机直线电机控制的应用结果证实它在提高系统动态性能方面的有效性[19-20]。那么，针对音圈FSM对指令的宽频带跟随要求和现有控制方法性能的限制问题，可以基于完全跟踪控制的思想给出更适合工程应用的控制器设计。

本文以音圈FSM为研究对象，构建了多速率采样系统并给出它适用的完全跟踪控制方法。针对鲁棒性和控制带宽的高要求，采用离散滑模内回路补偿控制器和多速率采样下前馈控制器相结合，提出了音圈FSM的完全跟踪控制方法。该方法有效提高了控制性能，解决了传统方法对闭环带宽的限制问题。

2 控制对象数学建模

音圈电机驱动FSM的物理结构如图1所示。反射镜通过柔性铰链与基座相连，通过控制反射镜两端的音圈电机伸缩实现反射镜的旋转运动。

图1 音圈快速反射镜物理结构Fig.1 Schematic diagram of VCM fast steering mirror

音圈FSM采用柔性铰链而非轴承结构作为基座与镜面的连接部件，柔性铰链的弹性力矩与反射镜的转动角度成正比。

根据音圈FSM物理特性建立系统控制模型的方框图，如图2所示。

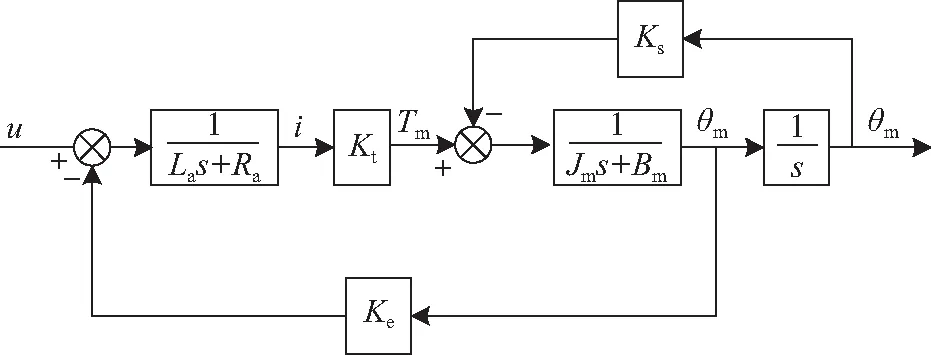
图2 FSM系统控制模型的方框图Fig.2 Block diagram of FSM system control model

图中，Ra为线圈电阻，La为线圈电感，i为线圈中的电流，Ke为反电动势系数，θm为电机转角，Tm为电机作用在反射镜上的力矩，Kt为电磁力常数，Jm为电机转动惯量，Bm为电机端黏性阻尼系数，Ks为柔性铰链的弹性系数。

根据图2求得被控对象的传递函数为：

(1)

实际系统中电机的电感非常小，可以忽略不计，因此式(1)可以简化成：

(2)

取状态变量x(t)=[x1(t)，x2(t)]T，x1(t)与x2(t)分别代表t时刻音圈快速反射镜的位置和速度。将上述传递函数转换成状态空间模型，如式(3)所示：

(3)

其中：

(4)

(5)

(6)

实际控制系统是在嵌入式处理器上以离散方式实现的，因此将公式(3)按采样周期Ts进行离散化得到离散状态方程：

(7)

其中：

(8)

控制器的设计将针对上述离散SISO系统开展。

3 控制器设计

本节利用系统的多速率采样特性，设计音圈FSM完全跟踪控制器(PTC)。控制器由基于短采样周期的内回路补偿控制器和基于长指令周期的前馈控制器组成。

3.1 多速率采样系统

为了保证音圈FSM的控制性能，其控制周期一般较短，而通常外部控制计算机发送给FSM控制器的指令周期要长于控制周期。因此，音圈FSM控制系统由长指令周期与短控制周期构成。指令周期Tr作为长周期部分，控制周期Tu和反馈采样周期Ty作为短采样周期部分[21-22]存在如式(9)所示的关系：

Tr>Tu=Ty=Ts.

(9)

指令周期与控制周期的不一致直接影响最终的控制性能。为了解决这一问题，通常采用插值的方式计算出iTr时刻与(i+1)Tr时刻之间的指令替代外部控制计算机的控制指令。为了更好地利用多速率采样特性，对长周期采样部分合理设计前馈，实现完全跟踪；对短周期部分设计合理的反馈以提高鲁棒性。两者结合实现对FSM的控制。

图3 多速率采样系统完全跟踪控制器结构Fig.3 Control structure of PTC with multi-rate sampling

图3为多速率采样系统完全跟踪控制器结构图。其中，CM(z)为前馈控制器，CM(z)为MIMO环节，CR(zs)为反馈控制器，CM(z)与CR(zs)共同作用，最终实现完全跟踪功能。L(t)为提升器，它按照短采样周期Ts依次输出其输入向量u[i]中的每个元素uk[i]，L(t)为MISO环节。根据式(2)可知FSM为二阶系统，因此可得：

u[i]=[u1[i]，u2[i]]T，

(10)

(11)

其中：Pc(s)为连续的被控对象，SM为采样器，HM为保持器。

3.2 长周期控制器设计

设定指令周期与短采样周期的关系为Tr=nTs，其中n为被控对象状态变量的个数，即被控对象的阶数。根据式(2)可知n=2，将按短采样周期Ts进行离散化得到的离散状态方程(7)进行转换，将短周期采样的SISO系统转换为长周期采样的MIMO系统：

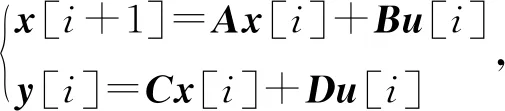
(12)

其中：

y[i]=[y1[i]，y2[i]]T，

(13)

(14)

由式(12)可以得到：

(I-z-1A)x[i+1]=Bu[i]，

(15)

当u[i]=B-1(I-z-1A)xd[i+1]时，就可以实现被控系统的状态对期望状态的完全跟踪。其中，xd[i+1]是下一时刻系统的期望状态，即：

x[i]=xd[i].

这样就得到前馈控制器：

CM(z)=B-1(I-z-1A)-CR(z)z-1C=
CM0(z)-CR(z)z-1C.

(17)

3.3 短周期控制器设计

考虑实际被控对象存在模型建模误差、外界干扰等因素，可以将图3中的短周期采样控制部分变换为图4所示的结构，通过加入对模型跟踪的反馈控制保证控制系统对干扰等不确定因素的鲁棒性。

考虑干扰后式(7)可以改写为如下形式：

(18)

其中dex(k)为等效干扰值。

图4 短周期采样控制结构的变形Fig.4 Structure deformation of short-cycle control

为了使系统具有更快的响应速度、更高的控制精度以及更强的抗干扰性能，在进行反馈控制器设计时，图4中的控制器CR(zs)可以采用离散滑模变结构控制方法[23]。

设系统的输入控制指令为r(k)，其对应的变化率为dr(k)，取R(k)=[r(k)，dr(k)]T；采用线性外推的方法预测r(k+1)以及dr(k+1)，即：

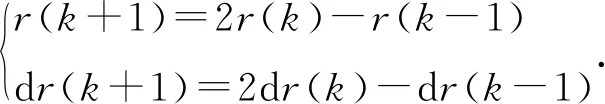
(19)

令滑模控制的切换函数为：

s(k)=Ce[R(k)-x(k)]，

(20)

其中Ce=[c1]。则：

s(k+1)=Ce[R(k+1)-x(k+1)]=
Ce[R(k+1)-Asx(k)-bsu(k)-bsdex(k)].

(21)

得到控制率为：

u(k)=(Cebs)-1[CeR(k+1)-
CeAsx(k)-s(k+1)]，

(22)

则基于指数趋近率的离散趋近率为：

s(k+1)=s(k)+Ts(-εsgn(s(k))-
qs(k))-Cebsdex(k).

(23)

将式(23)带入式(22)，得到离散控制率：

u(k)=(Cebs)-1[CeR(k+1)-
CeAsx(k)-s(k)-ds(k)]，

(24)

其中ds(k)=-Tsεsgn(s(k))-qTss(k)。

基于趋近率的离散滑模变结构控制器，可以通过调节控制参数q，ε，c实现控制器的设计。其中q为趋近速度参数，主要影响切换函数的动态过度过程，调节该参数可以改变系统向滑模面的趋近速度。ε为符号函数的增益参数，影响系统克服参数摄动以及外界干扰能力，该参数越大系统的抗干扰能力越强，但是过大的增益会导致系统抖振。c为滑模面参数，影响系统的调节时间，c越大系统的快速性越好，但是过大的滑模面参数会导致系统的抖动。

选取李亚普诺夫函数：

(25)

当公式(25)满足时，短周期控制系统能够稳定。

(26)

根据李亚普诺夫稳定性定理，s(k)=0全局渐近稳定，离散滑模的存在和到达性条件为：

[s(k+1)-s(k)]sgn(s(k))<0，
[s(k+1)+s(k)]sgn(s(k))>0.

(27)

由式(23)有：

[s(k+1)-s(k)]sgn(s(k))=
[-Tsεsgn(s(k))-qTss(k)-Cebsdex(k)]sgn(s(k)).

(28)

(29)

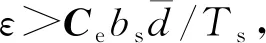
[s(k+1)-s(k)]sgn(s(k))<0.

(30)

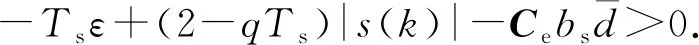
(31)

由此可见，当满足以上条件时，所设计的滑模控制率满足式(27)所示的离散滑模的存在和到达性条件，所设计的控制系统是稳定的。

4 实验与结果

4.1 实验设置

本文以音圈FSM为对象进行了实验验证，自研的音圈FSM如图5所示。音圈FSM口径为45 mm×35 mm，角度行程为±3 600″，反射镜控制系统以TMS320F28335数字信号处理器为核心，控制算法通过C语言进行编写。控制信号通过并行总线上的16位D/A转换器与功率放大器相连，镜面偏转角度的反馈信号通过A/D转换器进行采集，系统的采样与控制周期Ts=0.1 ms。

图5 音圈快速反射镜系统Fig.5 VCM fast steering mirror system

利用伪随机噪声和频谱分析的方法对控制对象传递函数进行辨识。图6为音圈FSM的开环系统模型。

图6 音圈快速反射镜开环系统模型Fig.6 Identification results of VCM FSM

通过扫频可以得到系统的模型参数如表1所示：

表1 音圈快速反射镜参数

通过上述参数拟合得到系统传递函数：

(32)

针对式(32)所示的被控对象进行长周期控制器以及内回路补偿控制器设计。首先，采用Tr=0.2 ms按照式(14)设计长周期控制器，控制器具体参数如式(34)、式(35)所示：

CM0(z)=B-1(I-z-1A)，

(33)

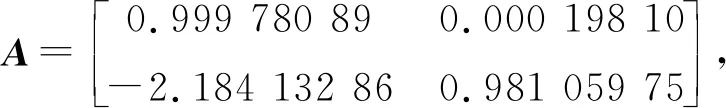
(34)

(35)

然后，采用Ts=0.1 ms对式(32)所示的被控对象按照式(8)进行离散化得到被控对象的状态空间表达式：

(36)

(37)

根据上述状态空间表达式，针对图 4中的内回路补偿控制器CR(zs)，采用累试法进行控制器设计，设计结果如下：

u(k)=(Cebs)-1[CeR(k+1)-CeAsx(k)-s(k)+
Tsεsgn(s(k))+qTss(k)]，

(38)

(39)

q=2 980.335 6，ε=1 845.537.

(40)

最后进行实验验证，对本文所设计的PTC控制器进行性能测试，分别对比传统PID控制、基于ZPETC和本文提出的PTC方法的实际控制效果。

4.1.1 静态定位精度测试

在静态定位精度测试中，通过对比3种控制器的稳态误差以及位置波动的峰峰值，衡量控制器的控制性能。

4.1.2 动态性能测试

在快速反射镜动态性能测试实验中，分别对比3种控制器的阶跃响应曲线和正弦跟踪曲线，通过实验结果衡量控制器性能。

4.1.3 系统带宽测试

通过正弦扫频测试对3中控制器的闭环控制带宽进行测试。

4.2 实验结果

4.2.1 静态定位精度测试

音圈FSM的静态定位精度是衡量反射镜性能的一项重要指标，直接影响光电成像设备的成像质量。

系统输入360″的恒值控制信号。从实验结果可以看出采用PID控制方法系统存在0.3%的稳态误差，反射镜的位置波动峰峰值为2.16″；采用ZPETC控制方法系统存在1.5%的稳态误差，反射镜的位置波动峰峰值为1.08″；采用PTC控制方法系统的稳态误差为0.05%，反射镜的位置波动峰峰值为1.08″。

从实验结果中可以看出，采用PTC控制方法相对于传统的PID控制方法，系统的位置稳态误差由0.3%减小到0.05%；相对于ZPETC控制方法，系统阶跃响应的调节时间缩短50%，系统的位置稳态误差由1.5%减小到0.05%，系统精度得到明显提升。

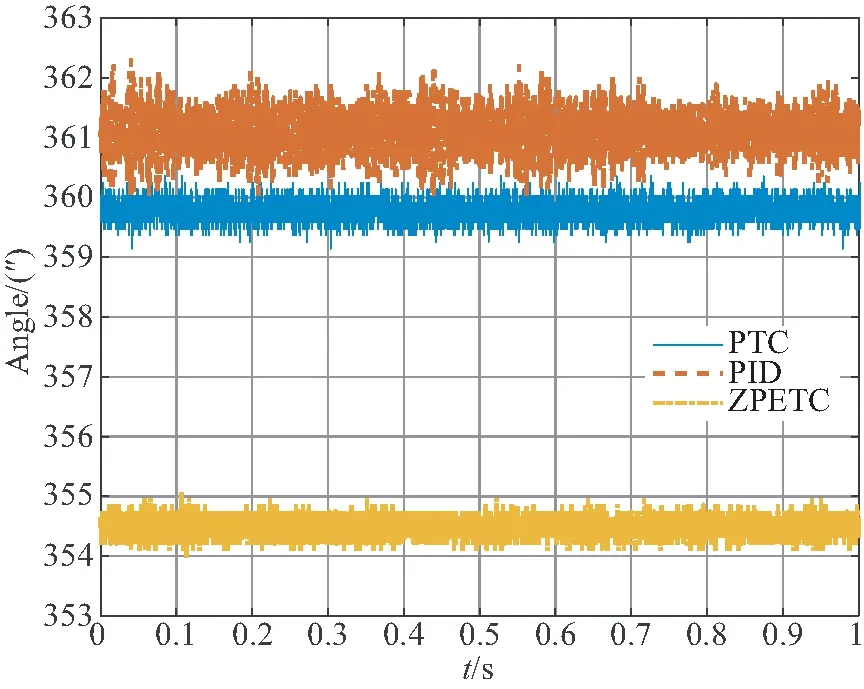
图7 静态定位精度测试结果Fig.7 Results of static positioning accuracy test

4.2.2 阶跃响应性能测试

动态性能是系统一个十分重要的指标，通过阶跃响应可以测定系统的动态性能。采用360″的阶跃位置指令作为期望轨迹信号进行跟踪实验。实验结果如图8所示。

从实验结果中可以看出，采用PID控制方法系统产生了52.8%的超调量，调节时间为14 ms；基于ZPETC方法的超调量为57.7%，调节时间为10 ms；而基于PTC控制方法的超调量为30.3%，调节时间为5.5 ms。采用PTC方法系统的阶跃响应性能明显好于PID和ZPETC方法。

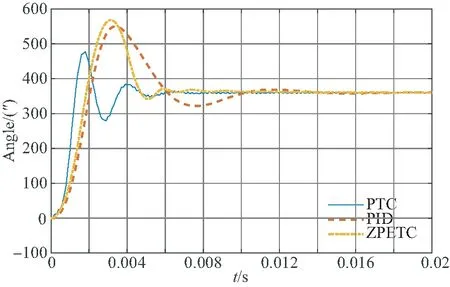
图8 阶跃响应性能测试结果Fig.8 Results of step response performance test

4.2.3 正弦信号跟踪性能测试

实验过程中采用PTC控制方法对频率分别为50，100，300 Hz，幅值为0.1°的正弦位置指令进行跟踪，实验结果如图9～图11所示。

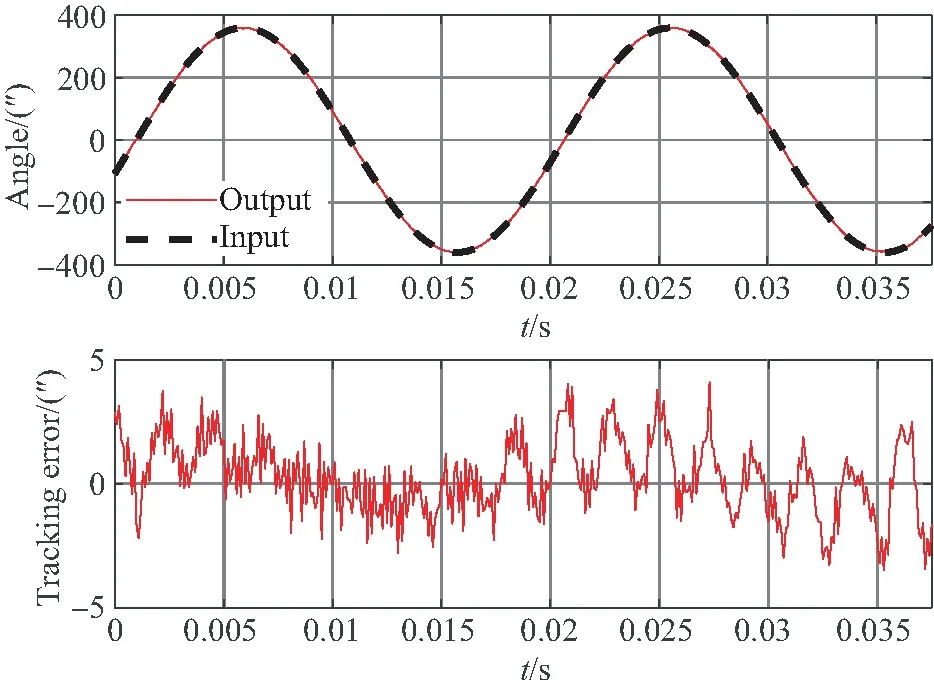
图9 50 Hz正弦信号的跟踪性能测试结果Fig.9 Tracking performance test results for 50 Hz sine signal

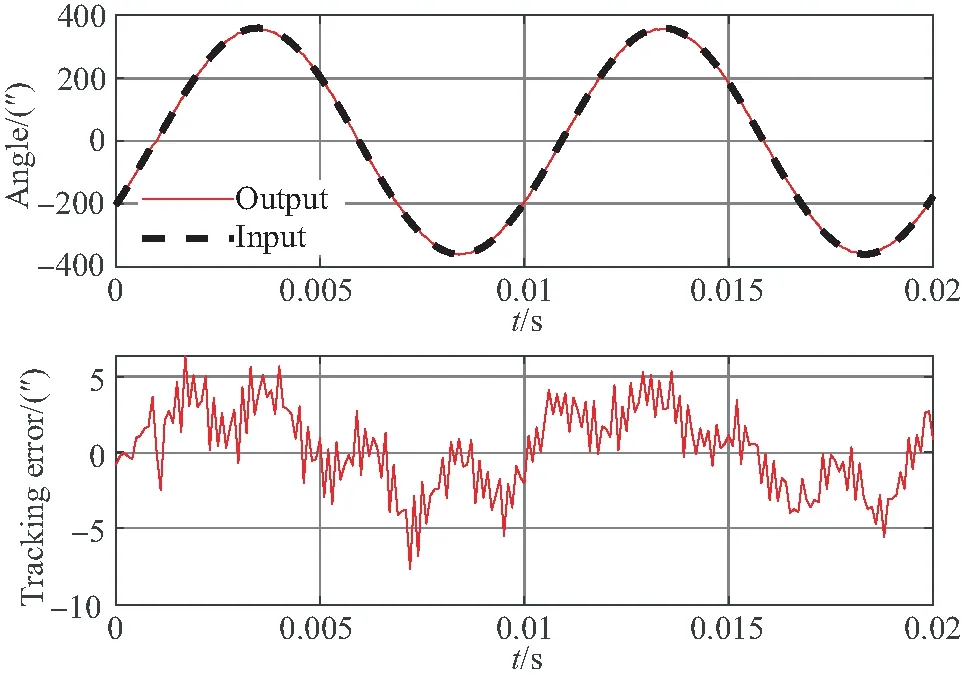
图10 100 Hz正弦信号的跟踪性能测试结果Fig.10 Tracking performance test results for 100 Hz sine signal

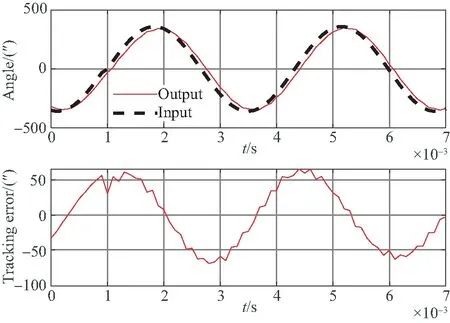
图11 300 Hz正弦信号的跟踪性能测试结果Fig.11 Tracking performance test results for 300 Hz sine signal

从实验结果中可以看出系统对指令的跟踪精度较高。

4.2.4 系统带宽测试

利用正弦指令输入对不同控制方法的闭环控制带宽进行测试，结果如图12～图14所示。

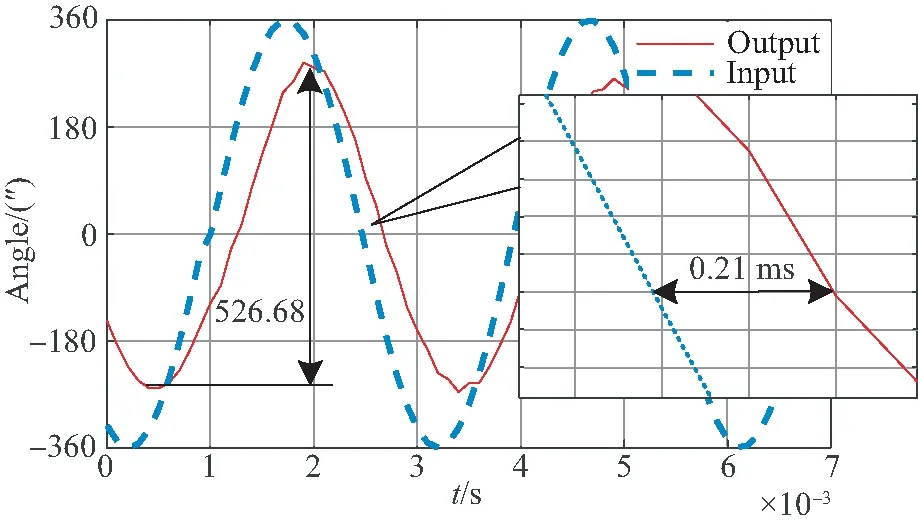
图12 基于PID控制方法的系统闭环带宽测试结果Fig.12 Closed-loop bandwidth test results for PID control

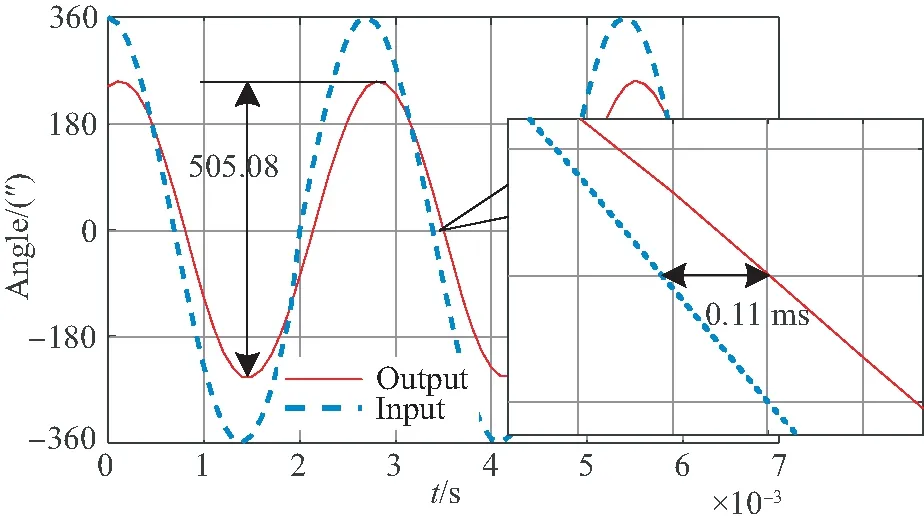
图13 基于ZPETC控制方法的系统闭环带宽测试结果Fig.13 Closed-loop bandwidth test results for ZPETC

图14 基于PTC控制方法的系统闭环带宽测试结果Fig.14 Closed-loop bandwidth test results for proposed PTC

由图12可以看出，采用传统PID控制方法，当输入正弦波频率为340 Hz时，幅值下降到-3 dB时，相位滞后25.704°，相位滞后严重。

由图13可以看出，基于ZPETC控制方法，当输入正弦波频率为360 Hz时，幅值下降到-3 dB时，相位滞后14.256°，相位滞后明显改善，但对300 Hz以上频率信号的跟踪仍然存在一定误差。

由图14可以看出，基于PTC控制方法，当输入正弦波频率为375 Hz时，幅值下降10%，相位滞后9.72°，动态特性得到了明显改善。

从实验结果可以看出，在相同的输入条件下，采用PTC控制方法相对于PID和ZPETC控制方法，在带宽拓展上有明显的提升。

5 结 论

本文针对音圈FSM设计了一种基于PTC的控制方法，实现了高精度、宽频带的FSM闭环控制。以某型音圈FSM为实际被控对象进行了实验验证，并与传统的控制方法进行了对比。实验结果表明，本文设计的PTC控制方法能够很好地保证反射镜的跟踪性能，相对于传统的PID控制方法，系统阶跃响应的调节时间缩短57%，系统的位置稳态误差由0.3%减小到0.05%，系统静态位置波动峰峰值减小50%；相比于ZPETC控制方法，系统阶跃响应的调节时间缩短50%，位置稳态误差由1.5%减小到0.05%；同时，采用PTC控制方法对幅值为360″的正弦指令进行跟踪性能测试时，系统的双十带宽(幅值下降10%，相位滞后10°)可以达到375 Hz。由实验数据可以看出，采用PTC控制方法，FSM的静态定位精度以及动态响应性能相对于PID控制方法以及ZPETC控制方法有明显的提高。本文设计的PTC控制方法可以有效抑制模型不确定性以及外部扰动的影响，提高系统的鲁棒性，同时弥补了外部指令周期与快速反射镜控制周期不同步的问题。