复杂荷载作用下高速铁路沥青混凝土层受力及开裂特性研究

吕宋，肖宏，张智海

(1.北京交通大学轨道工程北京市重点实验室，北京，100044；2.中国铁道科学研究院集团有限公司铁道建筑研究所，北京，100081)

高速铁路路基面铺设防水封闭层是一项重要的路基防水措施，可以有效阻止外界水向路基内部渗透，保证路基的承载力和稳定性，为高速铁路高平顺、高安全提供有力保障[1]。沥青混凝土因具有黏弹性好、柔性好、强度高、防水性能好等优点[2]，被广泛应用在美国、日本、德国等国家[3]。沥青混凝土在国内铁路领域的应用研究工作开展较晚，刚开始仅用于高速铁路无砟轨道路肩位置或线间位置的防水封闭层。如，在哈齐(哈尔滨—齐齐哈尔)、武广(武汉—广州)、郑徐(郑州—徐州)等高铁线路上铺设了试验段[2]。现场调研表明，部分地段沥青混凝土层开裂严重，裂缝扩展以横向为主。沥青混凝土层开裂会影响其长期服役性能，导致路基失稳，影响行车安全。为解决该问题，许多学者开展了一系列研究工作。王征[4]基于高寒地区高速铁路沥青混凝土防水封闭层的工作环境，发现高寒地区沥青混凝土应具有良好的防水性、抗裂性及高温稳定性，通过理论推导及沥青混凝土应用实例，提出东北高寒地区应选用改性沥青；邱延峻等[5]通过大量的马歇尔试验，分析了路基面防水层功能要求与沥青混合料力学行为之间的关系，提出了防水混合料SAMI(surface asphalt mixture impermeable)的技术指标体系，并研究了空隙率、沥青含量、级配等因素对SAMI材料渗透性能的影响；章天扬等[6]利用有限元软件，建立了3种轮轨噪声模型，通过计算和比较发现轮轨噪声随着沥青层厚度的增大而减小；方明镜等[7]利用有限元软件对沥青混凝土层及下部基础进行分析计算，指出提高沥青层弹性模量可以减小路基面竖向振动加速度，增加沥青层厚度和降低温度均能达到降噪效果。TEIXEIRA 等[8]利用美国肯塔基(KENTRACK)轨道模型对沥青混凝土使用性能进行分析，发现沥青底砟可以减小铁路沉降；ESMAEILI 等[9]对带热拌沥青混合料(HMA)底砟层的轨道模型进行仿真计算，得出了层间拉应变、路基层上压应力等结构设计参数。综上所述，目前已有研究主要从沥青混合料的配制方法及设计参数、使用范围、减振降噪性能等方面进行研究，而涉及沥青混凝层在长期服役过程中出现离缝、开裂等机理的研究较少，且对温度荷载作用下沥青混凝土的使用性能也关注较少，因而不能从受力机理上解释温度场-列车荷载耦合作用下沥青混凝土层的开裂现象。为此，本文作者基于黏弹性内聚力理论建立车辆-轨道-路基耦合的三维精细化有限元分析模型，对温度、列车荷载等复杂运营条件下沥青混凝土层的受力及开裂机理进行研究，分析底座板与沥青混凝土层的层间接触关系演变规律，提出改善沥青混凝土层服役性能的工程措施，以期为沥青混凝土层在铁路领域的推广应用提供参考。

1 沥青混凝土层间黏结破坏分析模型

1.1 黏弹性内聚力模型

内聚力模型是用来描述层间黏结面力与位移之间关系的物理模型[10-12]，如图1所示。由图1可知：直线OA与坐标轴所围成的区域为层间无损伤区域，在该区域内牵引力随着层间位移的增大而呈线性增长趋势，层间各处应力比破坏极限应力小，处于弹性阶段。随着牵引力F不断增大，逐渐逼近Fq(或者层间相对位移逼近临界位移δ0m,t)时，层间伤损萌生，此时，随着层间相对位移的增加，层间界面刚度逐渐减小，伤损逐渐累积；当层间界面的断裂能大于断裂韧度的极限值Gc(或者层间相对位移大于δfm,t)时，层间开始出现裂纹，原本黏结的层面由黏结接触关系退化为接触摩擦。

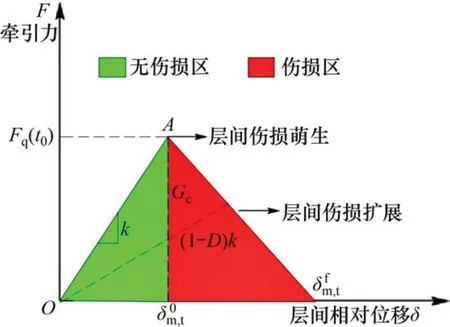
图1 层间内聚力模型Fig.1 Interlayer cohesion model

在无伤损区内，结构层面之间的力学响应以弹性作用为主，层间牵引力与位移关系的控制方程[13]为

式中：Fs和Ft分别为第一、第二切向牵引力；Fn为法向牵引力；ks，kt和kn为分别为第一、第二切向及法向刚度；δs，δt和δn分别为第一、第二切向及法向相对层间位移。在内聚力模型中伤损萌生一般表现为层间界面材料性能退化，产生微裂纹。本文参照已有研究[14]，采用最大应力准则作为层间伤损萌生的判定条件：

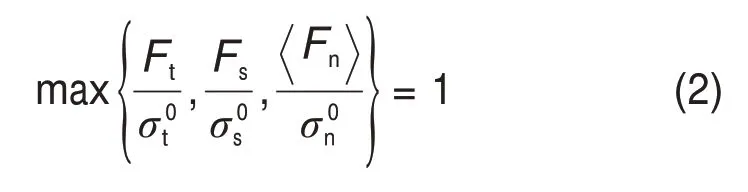
式中：和分别为第一、第二切向抗剪强度；为法向抗拉强度。参考文献[13]，引入损伤因子D来定量评价层间界面的伤损程度，其定义如下：

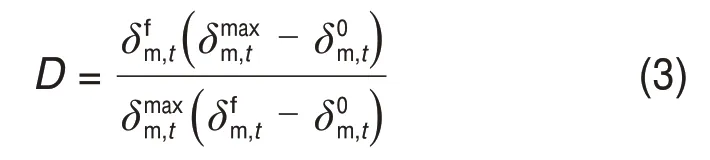
式中：为0～t时刻层间的最大有效位移，也是层间内聚力界面法向与切向变形的复合有效位移。损伤因子D的取值范围为[0，1]，当D=0时，层间无损伤；当D=1时，层间开裂、脱黏、完全损伤。

在伤损区内，结构层面的力学响应关系可用下式描述：

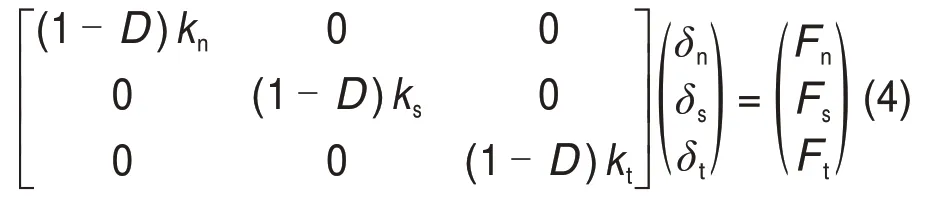
其中，δn>0。层间伤损演化及脱黏伴随着能量的变化，因此，可以将层间能量变化作为伤损演化的判断准则，如式(5)[15]所示：

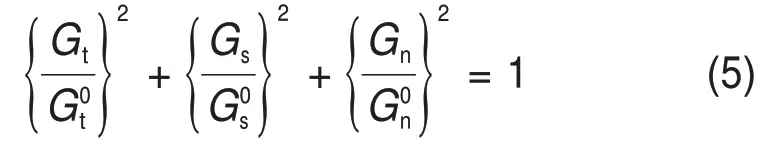
式中：，和分别为第一、第二切向及法向层间界面断裂韧度；Gt，Gs和Gn分别为第一、第二切向及法向层间界面能量，断裂能为σ(应力)-δ(有效位移)曲线与坐标轴所围成的面积。当层间能量的释放量达到断裂条件时，层间界面脱黏失效，层间接触关系退化为“硬接触”[16]和库仑摩擦[17]。

1.2 车辆-轨道-路基有限元模型

为考虑温度-列车荷载耦合作用对沥青混凝土层受力的影响，建立精细化车辆-轨道-路基三维耦合有限元仿真模型，如图2所示。针对沥青混凝土层的黏弹性及层间完全黏结性能，本文引入内聚力界面特性来模拟底座板与沥青混凝土层之间的相互作用，沥青混凝土层与基床表层之间采用共用节点方式连接[11]。参考文献[18]建立CRH-3动车组有限元模型。

图2 车辆-轨道-路基有限元模型Fig.2 Finite element model of vehicle-track-roadbed

CRTS III型板式无砟轨道各结构层采用实体单元进行模拟。考虑温度作用最不利效应，建模参数取值参考文献[18-19]，轨道板长度取5 600 mm，弹性模量为36 GPa，泊松比为0.2；自密实混凝土层，宽度为2 500 mm，厚度为90 mm，其长度与轨道板的相同，弹性模量为32.5 GPa，泊松比为0.2；路基直线地段底座板宽度为3 100 mm，厚度为300 mm，长度为11 320 mm，弹性模量为32.5 MPa，泊松比为0.2[20]。自密实混凝土与底座板之间用土工布隔开，摩擦因数取0.7[21]。参考文献[22]，底座板凹槽四周垫层刚度取30 kN/mm。

基床表层顶面宽度为8.6 m，高度为0.3 m，弹性模量为150 MPa，泊松比为0.3，密度为2 000 kg/m3。基床底层高度为2.3 m，弹性模量为100 MPa，泊松比为0.3，密度为2 000 kg/m3，沥青混凝土层厚度取8 cm。模型中热传递主要涉及到3种材料，热力学相关参数[1]如表1所示。

1.3 现场试验及模型验证

1.3.1 现场试验

为了获得底座板和沥青混凝土层的层间界面接触参数，在京张高铁河北省下花园北站附近开展现场足尺推板试验，如图3所示。由图3可知，在底座板一侧布置10台千斤顶同时施加横向推力，用位移传感器记录底座板及沥青层的位移变化；计算获得平均千斤顶推力为24.1 kN，最大剪切荷载约为241.0 kN。

表1 热力学参数[1]Table 1 Thermal parameters[1]

1.3.2 层间参数的确定及验证

在长期服役过程中，底座板和沥青混凝土层的层间内聚力以切向为主[1]。通过推板试验得到界面切向接触刚度Kss=25 MPa/m，法向接触刚度Knn=7×105MPa/m[10]，层间抗剪强度取1 200 kPa，抗拉强度取261 kPa[4]。

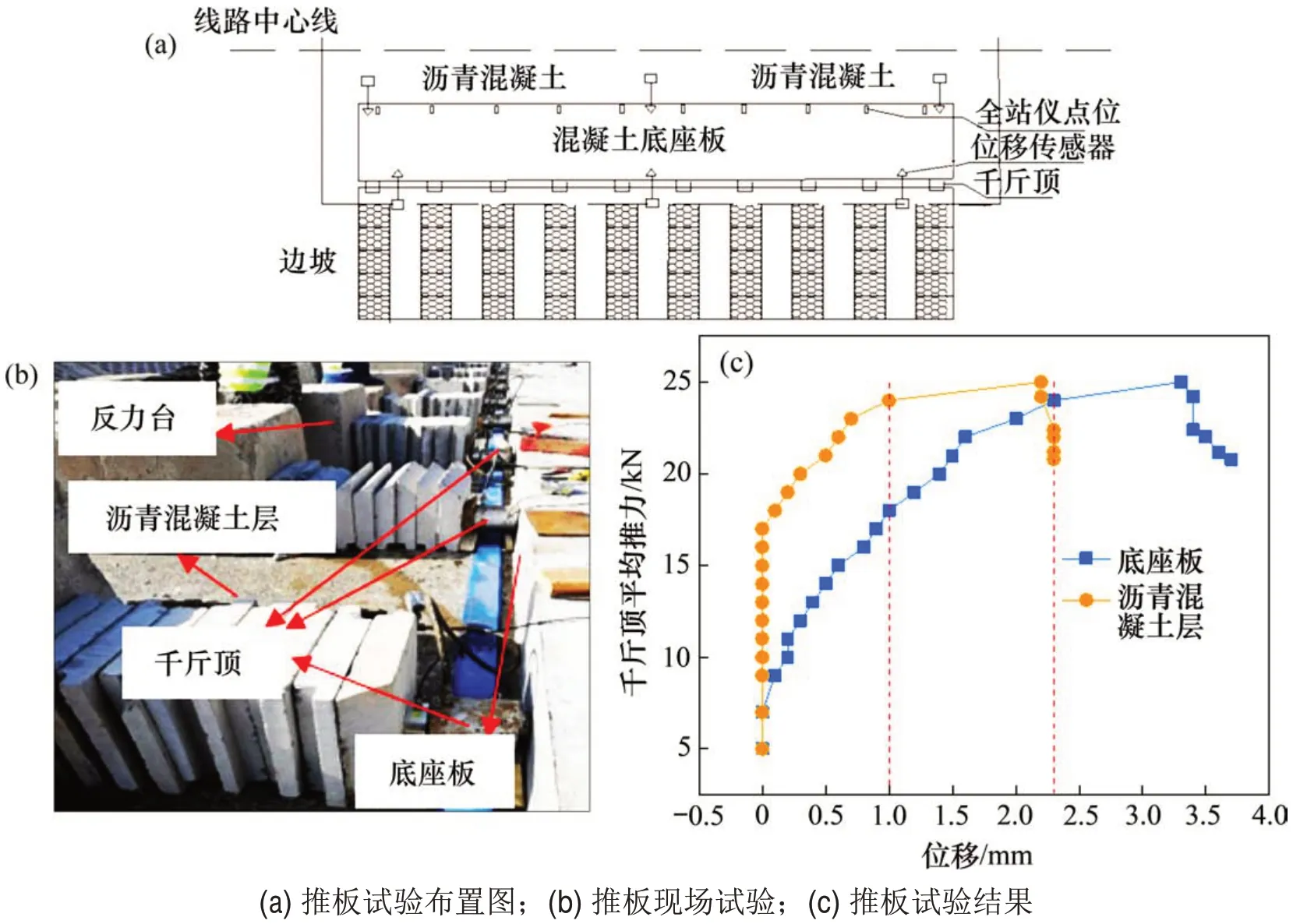
图3 推板试验Fig.3 Shear test

为验证沥青混凝土层层间参数取值的正确性，建立推板试验的有限元仿真模型，如图4所示。推板试验横向推力试验值与仿真值见图5。由图5可知：横向推力仿真计算最大值为246 kN，试验最大值为241 kN，两者相差不大；在初始阶段，横向推力试验值与模拟值有所差别，当横向位移大于0.36 mm时，两者变化几乎一致。这是因为在数值模拟中对于推板试验时的温度等外界条件考虑不足，且黏弹性内聚力模型本身与现场实际存在一定区别。软化阶段横向推力仿真值比试验值略小，这是由于仿真模型本身为近似线性软化模型，对混凝土本身软化变形过程进行了近似线性化处理，而在现场试验中千斤顶同时加载过程不易控制，横向推力试验值在软化阶段呈曲线变化。因此，在误差允许的范围内可以认为层间内聚力参数取值是合理的。

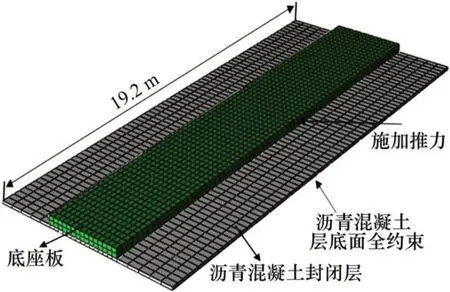
图4 推板试验有限元仿真模型Fig.4 Finite element model of shear test

图5 横向推力试验值与仿真值Fig.5 Comparison of experimental and simulated horizontal thrust

1.3.3 有限元模型验证

为验证车辆-轨道-路基三维有限元模型的正确性，参照文献[23]以及郑徐高铁开封段沥青混凝土层试验段实际运营情况，动力仿真计算列车速度取250 km/h，获得路基基床表层动位移时程曲线，如图6所示。由图6可知，仿真计算基床表层动位移最大为0.52 mm，文献[23]测得基床表层动位移最大为0.50 mm，二者相对误差仅为4%，在误差允许的范围内，故认为模型可以较好地反映现场实际情况。

2 温度梯度对沥青混凝土层受力性能的影响

在长期服役过程中，沥青混凝土层温度梯度呈周期性变化，导致层间伤损累积，使用寿命下降，严重影响路基的稳定性及线路的平顺性。本文研究温度梯度荷载下沥青混凝土层的受力时，参考文献[1]，考虑最不利荷载情况，取正温度梯度为90 ℃/m，负温度梯度为45 ℃/m。

2.1 正温度梯度荷载

图7所示为正温度梯度荷载作用下沥青混凝土层的应力应变分布云图。由图7(a)可知：沥青混凝土层最大Mises应力为36.470 kPa，最小Mises应力为2.563 kPa；应力主影响区位于底座板伸缩缝及中间位置，且板中位置应力比底座板边缘的小。由图7(b)可知：沥青混凝土层最大主应变为-6.302×10-4，最小主应变为底座板非接触区域，应力与应变分布规律极为相似。这是由于在正温度梯度荷载作用下底座板内部温度不均匀发生垂向翘曲变形，且沥青混凝土与底座板之间在无温度荷载时处于完全黏结状态，底座板的翘曲和变形会扰动沥青层的受力状态，因此，在温度荷载作用下，底座板会将翘曲作用力传递给沥青混凝土层，当层间翘曲应力超过层间内聚应力时，发生层间分离。底座板混凝土与沥青混凝土属于不同材料，其抗拉与抗压性能存在显著差异，且温度越高，沥青混凝土弹性模量越低[1]，抵抗变形能力越弱，使得层间变形协调能力下降；当与底座板处于相同温度应力条件时，沥青混凝土层产生较大的应变，导致层间出现离缝及表层开裂现象。

为研究正温度梯度作用下底座板伸缩缝处沥青混凝土层的应力、应变在纵向和横向的分布规律，以伸缩缝位置为坐标原点，绘制沥青混凝土层的应力、应变与纵横向距离的关系曲线，如图8所示。

图7 正温度梯度作用下沥青混凝土层应力、应变分布Fig.7 Stress and strain distribution of asphalt concrete layer under positive temperature gradient

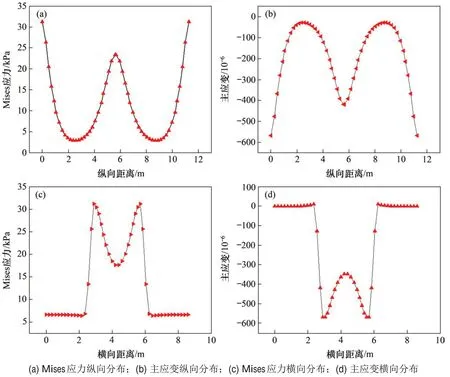
图8 不同距离下沥青混凝土层应力应变分布(正温度梯度荷载)Fig.8 Distribution of stress and strain in asphalt concrete layer at different distances(positive temperature gradient load)

由图8可知：在底座板伸缩缝位置处，沥青混凝土层纵向Mises应力先减小后增大，然后减小又增大，边缘应力最大，中部应力次之，呈“W”形分布，而主应变的分布呈“M”形分布。沥青混凝土层横向Mises应力在底座板边缘有效接触区内先增大后减小，然后增大又减小，有效接触区边缘应力最大，中部应力次之；主应变的分布与Mises应力分布规律相同。由此可见，沥青混凝土层的温度主影响区位于底座板有效接触区的边缘和中部，温度敏感区处于底座板边缘有效接触区的边角位置，以底座板纵横向中心线为对称轴，呈对称分布。

2.2 负温度梯度荷载

图9所示为沥青混凝土层在负温度梯度荷载作用下的应力、应变分布云图。由图9(a)可知：沥青混凝土层最大Mises应力为25.070 kPa，最小Mises应力为1.799 kPa；应力主影响区位于底座板有效接触区的中部，该位置的应力比边缘处的大，且沿底座板中心点位置呈“圆环状”扩散。由图9(b)可知：沥青混凝土层最大主应变为-4.751×10-4，最小主应变位于底座板非接触区域，其分布规律与应力分布相似。这是由于温度越低，沥青混凝土弹性模量越高，抵抗变形能力逐渐增强，但层间界面材料属性不同，抗温变的能力也不相同，导致层间变形协调性能减弱，且负温度梯度荷载作用下底座板内部产生与正温度梯度作用相反的垂向翘曲变形，当层间翘曲应力超过层间内聚应力时，可能出现层间分离。

图10所示为负温度梯度下沥青混凝土层的应力应变在纵横向的分布规律曲线。由图10可知：沥青混凝土层纵向Mises应力先增大后减小，再增大又减小，底座板中心点处沥青层的应力最大，边缘位置应力较小，呈“M”形分布，而主应变呈“W”形分布。沥青混凝土层横向Mises 应力和最大主应变均先增大后减小，前者呈“倒V”形分布，后者呈“V”形分布。由此可见，沥青混凝土层的温度主影响区和温度敏感区都位于底座板有效接触区中部。

通过与2.1 节正温度梯度荷载作用对比发现，负温度梯度作用下Mises应力和主应变都较小，且温度敏感区处于底座板有效接触区中部，层间黏结性能好，出现层间分离及开裂的概率较低，因此可以认为正温度梯度荷载是影响沥青混凝土层层间分离及开裂的主要因素。

3 复杂荷载作用下沥青混凝土层裂纹扩展类型

裂纹扩展有3种类型，即张开型(I型)、滑移型(II型)和撕开型(III型)裂纹，如图11所示。图11中σ为法向应力，τ为切向应力。构件一旦开裂，不管外力多小，裂纹尖端区域应力的解析解趋于无穷大[1]。层间结构脱黏后，在复杂荷载作用下裂纹会扩展延伸，使结构的抗疲劳性能减弱。

3.1 温度荷载作用下沥青层裂纹扩展特性

沥青混凝土层的使用性能受温度影响很大，为研究温度对沥青层裂纹扩展的影响，考虑不同位置的裂纹扩展方向的差异性，在底座板伸缩缝位置预设3 条长度为1 m、深度为0.05 m 的裂纹，分别位于L1，L2和L3处，如图12所示。以温度骤降法为例研究应力强度因子与温度之间的变化关系，并确定裂纹扩展类型，降温幅度介于0～20 ℃。参考每日气温变化时间，降温时间取10 h。

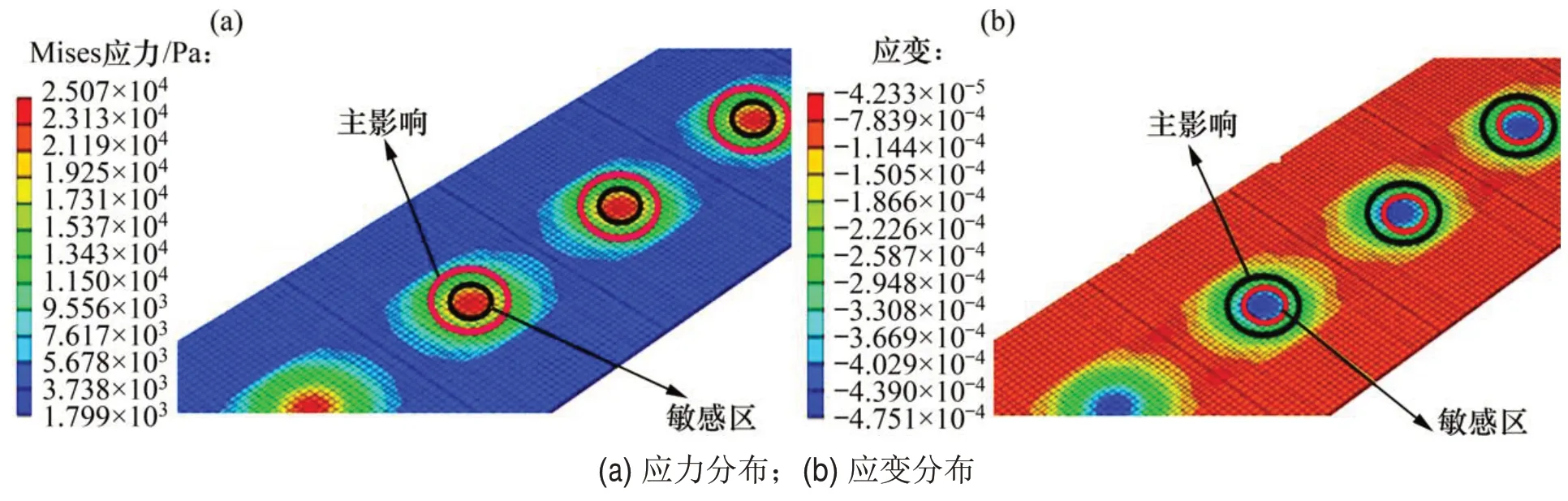
图9 负温度梯度作用下沥青混凝土层应力、应变分布Fig.9 Stress and strain distribution of asphalt concrete layer under negative temperature gradient

图13所示为L1处温度骤降过程中应力强度因子的变化曲线。由图13可知，随着温度逐渐降低，Ⅰ型裂纹的应力强度因子KⅠ呈线性增大趋势，最大值为944.5 kPa·m0.5，而KⅡ和KⅢ几乎无变化，说明低温条件下，沥青层裂纹扩展以张开型裂纹为主。

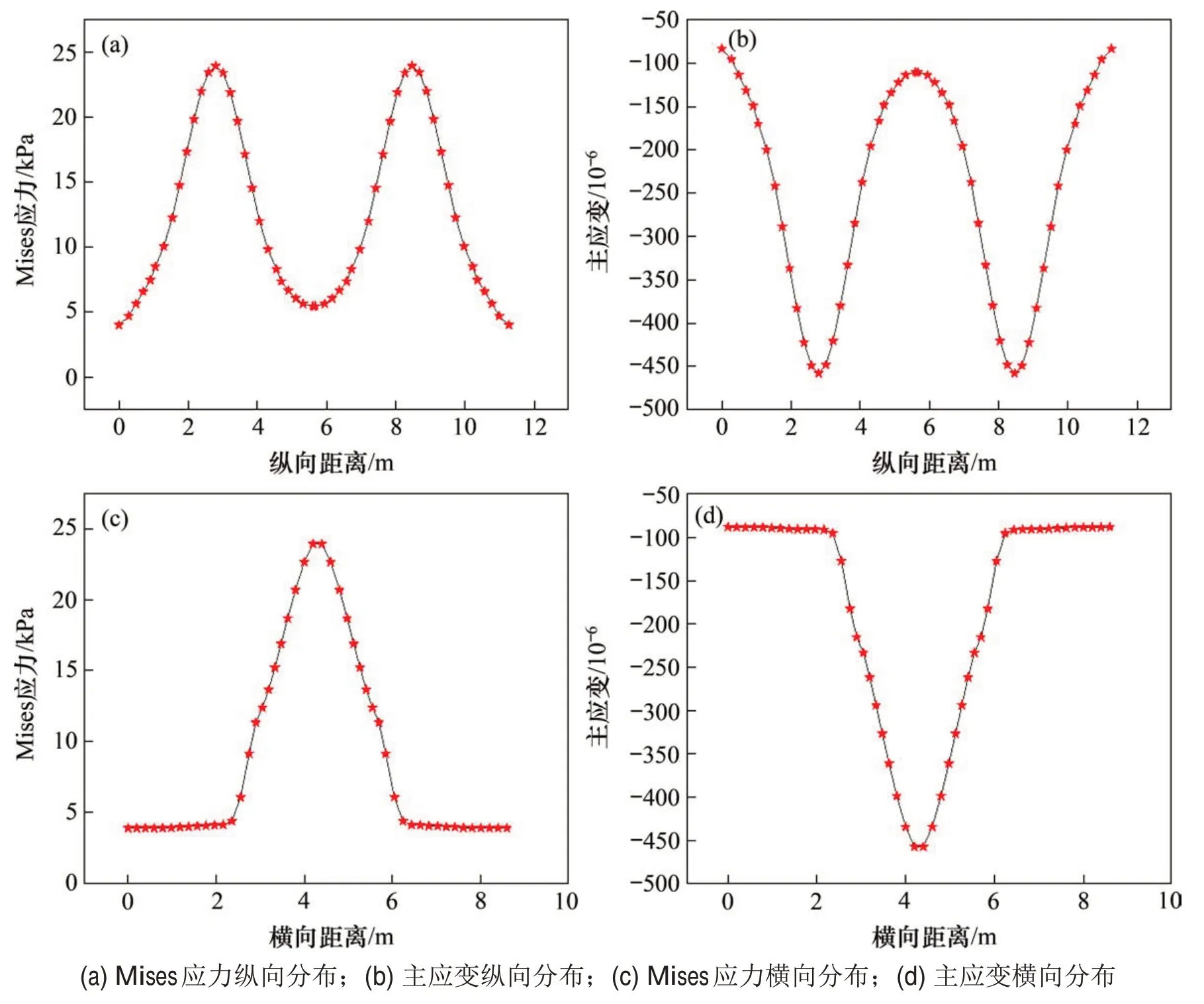
图10 不同距离下沥青混凝土层应力应变分布(负温度梯度荷载)Fig.10 Distribution of stress and strain in asphalt concrete layer at different distances(negative temperature gradient load)

图11 裂纹扩展类型Fig.11 Crack propagation type

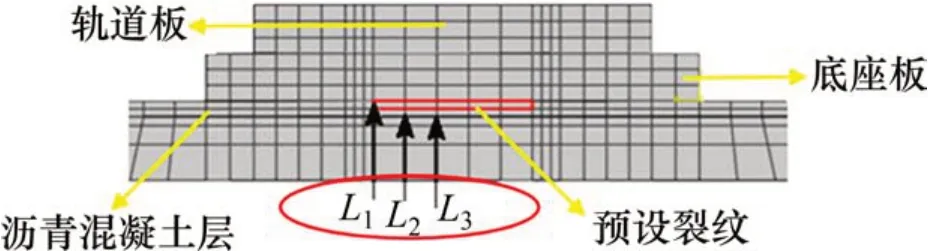
图12 预设裂纹位置示意图Fig.12 Diagram of preset crack location

图13 温度骤降过程中应力强度因子变化Fig.13 Stress intensity factor changes in temperature sag process

在低温作用下沥青混凝土层易发生Ⅰ型开裂，但是预设裂纹的不同位置扩展延伸方向并不相同，L1处裂纹沿水平方向扩展，L2和L3处裂纹均沿竖向延伸扩展。图14所示为不同位置处应力强度因子KⅠ与温度的关系曲线，图15所示为不同位置处J积分值(裂纹尖端应力应变场的能量)与温度的关系曲线。由图14和图15可知：随着温度逐渐降低，L1，L2和L3处的KⅠ呈增大趋势，L3的增幅最大，L2次之，L1增幅较小；随着温度逐渐降低，L2和L3处的J 积分值逐渐增大，L1处的J 积分值几乎无变化，说明张开型裂纹沿竖向扩展比水平扩展更容易，裂纹在扩展过程中先沿竖向延伸再沿水平方向扩展，从而可能会形成复杂的交叉裂纹扩展现象。

图14 温度骤降过程中应力强度因子KⅠ变化Fig.14 Stress intensity factor KⅠchanges in temperature sag process

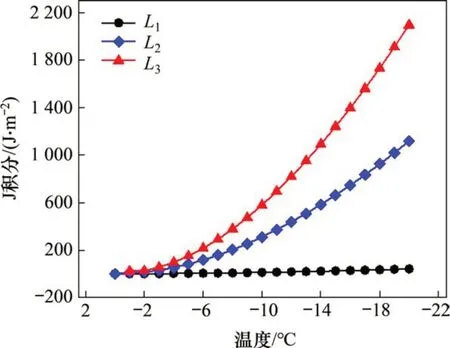
图15 温度骤降过程中J积分值变化Fig.15 J integral changes in temperature sag process

3.2 温度-列车荷载耦合作用下沥青层裂纹扩展特性

沥青混凝土材料被用于铁路路基防水封闭层时，因处于温度与列车荷载耦合作用场，受力及裂纹扩展特性复杂多变，疲劳寿命难以预估。因此，在分析沥青混凝土的受力及开裂性能时，应该综合考虑温度与列车荷载的影响。本文基于扩展有限元方法，在进行温度-列车荷载耦合计算时，分别考虑了低温0 ℃和高温40 ℃这2种工况。

图16(a)所示为低温场张开型裂纹应力强度因子随时间的变化曲线，图16(b)所示为L3处低温场滑移型裂纹应力强度因子随时间的变化曲线。由图16可知：L1处KⅠ平均值为7.5 kPa·m0.5，为正值且比较小，不能改变材料的力学特性；L3处的KⅠ在-27.5 kPa·m0.5上下波动，为负值，说明L3处受压，不可能出现张开型裂纹；L3处的应力强度因子KⅡ在[-51.0，-68.4]kPa·m0.5之间，且随着时间延长，有逐渐增大的趋势。从裂纹发生的概率考虑，低温场-列车荷载耦合作用下沥青混凝土层不易出现张开型横向裂纹，有可能导致伸缩缝位置处出现横向滑移型裂纹。

图17(a)所示为高温场张开型裂纹应力强度因子L随时间的变化曲线，图17(b)所示为L3处高温场滑移型裂纹应力强度因子随时间的变化曲线。由图17可知：L1处KⅠ为-1.50 kPa·m0.5，L3处的KⅠ为-4.75 kPa·m0.5左右，均为负值，因此，不可能出现张开型裂纹。L3处的应力强度因子KⅡ在[-70，-220]kPa·m0.5之间，且随着时间延长，应力强度因子KⅡ逐渐增大，从裂纹发生的概率考虑，高温场-列车荷载耦合作用下沥青混凝土层易出现横向滑移型裂纹。与低温条件相比，高温条件L3处的应力强度因子KⅡ大，且随时间的变化幅度也较大，这是由于温度对沥青混凝土的黏弹性影响显著，温度越高，裂缝位置处受到的剪切力越大，故横向滑移型出现的可能性越大。

为了研究沥青混凝土层纵向裂纹的扩展类型，在模型中预设长度为1 m、深度为0.05 m的纵向裂纹，如图18所示。由于纵向裂纹主要承受列车动荷载的剪切作用，因此，易出现纵向滑移裂纹。图19所示为伸缩缝位置处的应力强度因子KⅡ与时间的关系曲线。由图19可知：应力强度因子KⅡ随着时间的增加而逐渐增大，且在相同时间点，纵向裂纹KⅡ较横向裂纹KⅡ大，说明纵向滑移裂纹比横向更容易扩展。

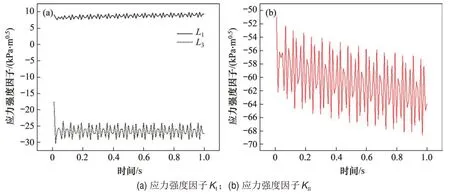
图16 低温场张开型裂纹应力强度因子随时间的变化Fig.16 Changes of stress intensity factor of open crack in low temperature field with time

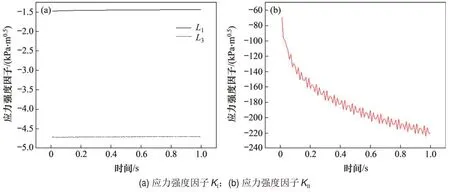
图17 高温场张开型裂纹应力强度因子随时间的变化Fig.17 Changes of stress intensity factor of open crack in high temperature field with time

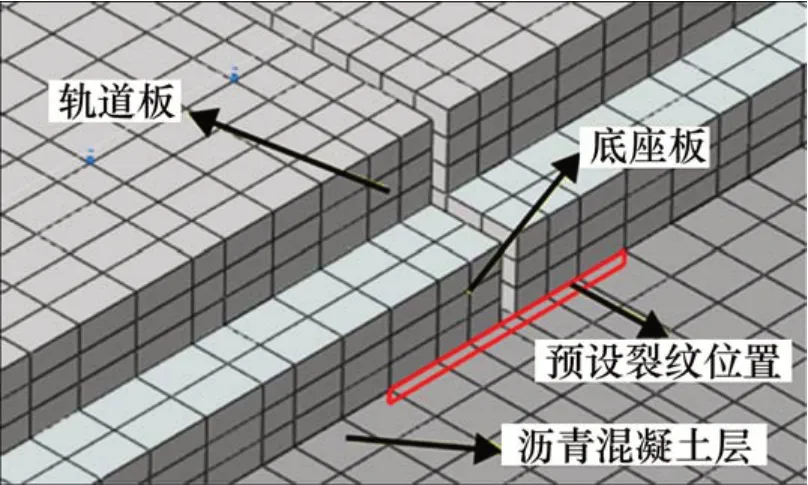
图18 纵向裂纹位置Fig.18 Longitudinal crack position

4 改善沥青混凝土层受力特性

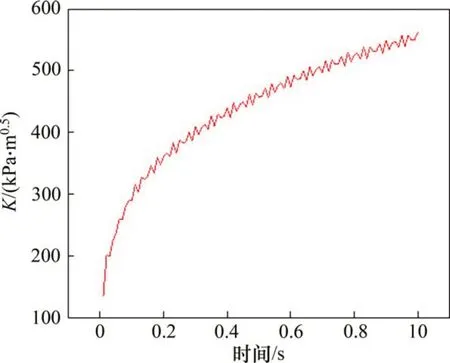
图19 伸缩缝位置处应力强度因子KⅡ随时间的变化Fig.19 Changes of stress intensity factor KⅡat the expansion joint with time

沥青混凝土层在温度与列车荷载作用下层间易出现伤损、黏结退化、裂纹扩展等现象，严重影响线路的正常服役性能。本文借助最大应力准则[1,11]的初始损伤量(Co)来判断层间伤损敏感区，如图20所示。由图20可知：底座板边缘初始损伤量最大，中部损伤量较小，可以认为底座板边缘位置为敏感区，层间黏结易退化。为改善沥青混凝土层的长期服役性能，延长其疲劳寿命，避免底座板敏感区过早开裂，特提出在底座板伸缩缝处一定范围内铺设复合土工膜，来减小敏感区的应力应变。在底座板敏感区域分别铺设长度为0.30，0.50，1.00，1.25，1.50，2.00 m的复合土工膜滑动层，如图21所示。

图20 底座板下Co分布Fig.20 Distribution of Co under the base plate

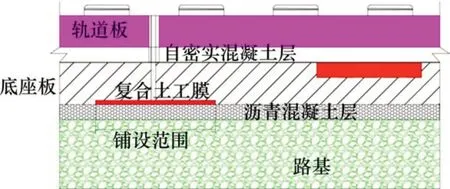
图21 土工膜滑动层铺设区域示意图Fig.21 Diagram of geomembrane sliding layer area

考虑温度荷载对沥青混凝土层受力及参数的影响，计算时将沥青混凝土层温度设置为一定值，只研究在底座板与复合土工层在整体降温荷载作用下的沥青混凝土应变分布规律，结果分别如图22和图23所示。

由图22和图23可知：随着复合土工膜铺设长度增大，底座板敏感区位置沥青混凝土层的应变显著减小，高应变区域逐渐消失，在铺设复合土工膜的区域内其应变分布均匀，说明复合土工膜可以有效控制沥青混凝土层应力、应变增大。这是由于在底座板边缘铺设土工膜滑动层减小了底座板边缘对沥青混凝土层的牵引力，使受拉区域变大，故沥青混凝土层的应变幅值显著减小。

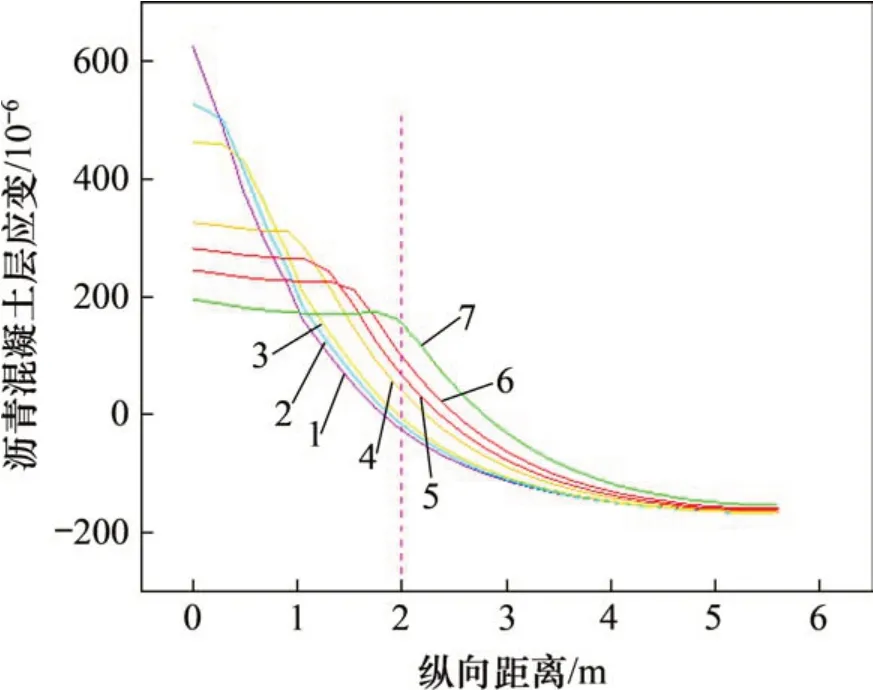
图22 不同铺设长度下应变纵向分布Fig.22 Longitudinal distribution of strain under different laying lengths

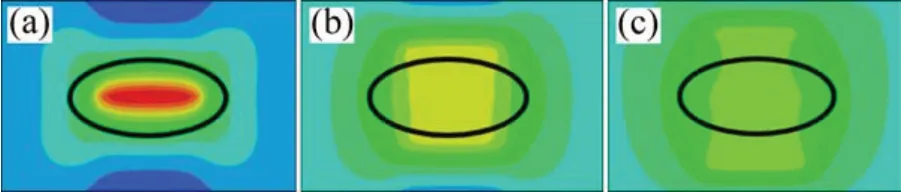
图23 不同铺设长度下应变分布云图Fig.23 Cloud chart of strain distribution under different laying lengths

为确定复合土工膜的合理铺设长度，对不同铺设长度下沥青混凝土层的应变降幅进行统计，如图24所示。由图24可知：随着铺设长度的增加，沥青混凝土层应变降幅逐渐收敛并趋于稳定；当铺设长度大于1.5 m 时，应变降幅收敛程度较大，坡度变缓；当铺设长度小于1.0 m时，应变降幅急剧增长，但应变降幅未超过50%，作用效果一般；当铺设长度在1.0～1.5 m 时，应变降幅呈线性增大，且大于50%。考虑复合土工膜对沥青混凝土层的作用效果，铺设长度不可太短；从工程的经济性和施工的难易程度考虑，复合土工膜层铺设长度不宜过长。

因此，基床表层全断面铺设沥青混凝土封闭层时，CRTSⅠ型、CRTS Ⅲ型等底座板伸缩缝两侧建议增加复合土工膜，本文建议合理铺设长度为1.0～1.5m。

图24 应变减小幅度与铺设长度的关系Fig.24 Relationship between strain reduction and slip layer length

5 结论

1)在正温度梯度作用下，沥青混凝土层最大应力为36.470 kPa，最大应变为-6.302×10-4，温度敏感区位于底座板边缘有效接触区的边角位置；在负温度梯度作用下，沥青混凝土层最大应力为25.070 kPa，最大主应变为-4.751×10-4，在负温度梯度作用下，最大应力和应变都较小，且温度敏感区位于底座板有效接触区中部，层间黏结性能好，说明正温度梯度是导致沥青混凝土层层间分离及开裂的主要因素。

2)当温度骤降时，Ⅰ型裂纹的应力强度因子KⅠ呈线性增大而KⅡ和KⅢ几乎无变化；张开型和滑移型裂纹的J积分值逐渐增大，而撕开型裂纹几乎无变化，说明在低温条件下，沥青层裂纹扩展以张开型裂纹为主；张开型裂纹沿竖向扩展比水平扩展更容易，裂纹在扩展过程中先沿竖向延伸再沿水平方向扩展，从而可能会形成复杂的交叉裂纹扩展现象。

3)在低温场-列车荷载耦合作用下，沥青混凝土层不易出现张开型横向裂纹，可能出现横向滑移型裂纹；高温场-列车荷载耦合作用下沥青混凝土层易出现横向滑移型裂纹。由于纵向裂纹主要承受列车动荷载的剪切作用，因此易出现纵向滑移裂纹；在相同时间点，纵向裂纹KⅡ较横向裂纹KⅡ大，说明纵向滑移裂纹比横向裂纹更容易扩展。

4)伸缩缝位置铺设复合土工膜可有效减小敏感区的应力应变，改善沥青混凝土的长期服役性能。考虑复合土工膜对沥青混凝土层的作用效果，以及工程的经济性和施工的难易程度，本文建议复合土工膜的合理铺设长度为1.0～1.5 m。