五自由度混联3D打印机设计与运动学分析

(福州大学机械工程及自动化学院，福建福州，350116)

3D 打印因其高效、清洁、材料利用率高等优点，已被逐步应用于生物医学、复杂产品制造等领域[1-3]。目前，较为成熟的3D打印技术有熔融沉积成型(FDM)、激光选区烧结(SLS)、光固化成型(SLA)等。其中，FDM 形式的3D 打印机器人以低成本、高效率、打印路径和结构简单等特点得到广泛应用，然而，这种打印技术仍存在一些缺点[4-5]：1)打印的产品表面精度不高，易出现台阶效应；2)打印头姿态固定不能生成较复杂的零部件并且需要较多的支撑材料；3)对于已打印的产品不能进行二次修复等。国内外学者提出采用多向3D 打印技术来解决上述打印过程中出现的问题，目前对于多向3D 打印技术从以下2 个方面来实现：1)增加3D 打印机器人末端执行器的自由度，如LEE 等[6-7]设计了混联五轴加工和快速成型一体的机床，通过转动工作台和打印头实现多向3D打印，有效地提高了打印质量；潘英等[8]设计了一种能实现大范围移动和转动的五自由度3D打印机器人，解决了一般并联机构工作空间小、转动能力差的问题，进而使末端执行器具有多向3D打印的能力。SONG 等[9]将并联机构应用于3D 打印，使得末端执行器以倾斜角度运动，进而实现多向打印。YE等[10]基于可重构并联机构的可重构特性、高刚度和高运动特性等，提出一种多向3D打印的可重构并联机构，其实验分析结果表明，所提出的并联机构能很好地完成多向3D打印任务。2)通过旋转打印平台实现多向3D打印，如SINGH等[11]采用柔性机构为工作平台，配合xyz三轴运动的打印头以实现多向分层打印。GAO 等[12]提出的RevoMaker 3D 打印机通过转动方形平台实现多向和多功能3D打印，实现定制化和多功能模型的打印。目前，3D 打印机一部分采用串联式的机构，但是该类机构存在误差累积、悬臂刚度低等特点，打印效果并不理想。而采用并联式的机构如Delta和Stewart 机构等又容易出现受并联机构本身结构限制、工作空间小等问题，使得大尺寸产品的打印受到约束[13]，因此，研究能满足多向3D 打印的并联机构具有重要意义。在并联机构当中，2R1T型冗余并联机构以机构/运动学简单、控制容易、工作空间较大等特点备受青睐[14-18]。汤腾飞等[19]分析了类Exechon 和Exechon 并联机构运动学性能，发现该并联机构具有较好的运动学特性和较大的工作空间，能够调整机构姿态，达到不同工程应用的目的。鉴于这类并联机构的大姿态转角和良好的运动学特性，本文作者提出一种五自由度混联3D 打印机，其中，拓扑构型为以2UPR&2RPS的冗余驱动并联机构为主体的模块，以实现打印头调姿。为了扩大3D打印工作空间和克服并联机构在xy方向运动范围的限制，混合串联十字运动平台在保证多向3D打印的同时，将最大限度地增大复杂形状打印产品的尺寸。最后，本文作者对所设计的五自由度混联3D打印机的自由度、运动学正逆解、工作空间、奇异性和运动仿真分析等运动性能进行研究，以期为多向3D打印提供一种新的技术方案。

1 结构设计与描述

图1所示为五自由度混联3D 打印机模型。整体构成由对称布置的2UPR&2RPS并联机构、十字运动平台、料架、挤出器、打印头和机架组成。料架上的打印材料通过挤出器连接于并联机构动平台上的末端执行器(即打印头)上，打印头通过并联机构和十字运动平台的协同作用实现多向3D打印。

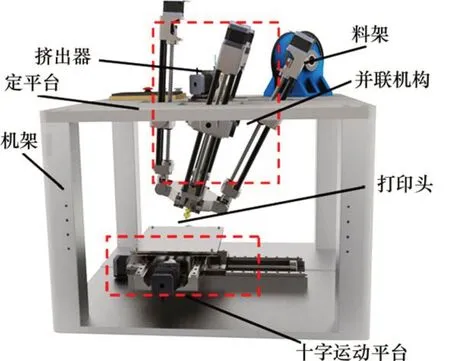
图1 五自由度混联3D打印机虚拟样机模型Fig.1 Virtual prototype model of the 5-DOF hybrid 3D printer

为了满足3D 打印机轻巧、模块化的需求，设计主体模块为2UPR&2RPS 的并联机构，如图2所示，可见该并联机构由定平台、动平台(含打印头)、2 条对称分布的RPS 支链和2 条UPR 支链组成。在4条支链中，在不改变支链运动性质的情况下，以降低支链体运动惯量为主要目标，采用碳纤维杆为支撑形式，将模块化的虎克铰、转动关节、球铰组合成UPR 和RPS 的支链布置式，实现支链体轻量化和模块化支链的设计思路。

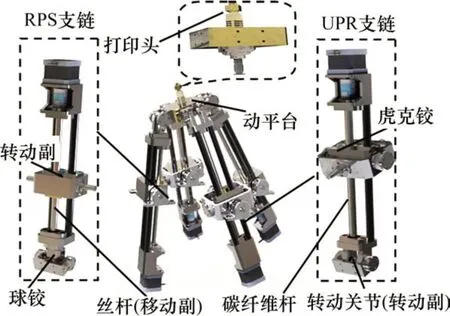
图2 2UPR&2RPS并联机构虚拟样机模型Fig.2 Virtual prototype model of 2UPR&2RPS parallel manipulator

其中，UPR 支链的虎克铰(U 副)与定平台连接，且2条支链的U副第一转轴共线，转动关节(R副)与动平台连接，驱动副(P副)轴线通过虎克铰中心点和R副中心点且分别垂直于U副第二转轴和R副转轴。在2 条RPS 支链中，R 副与定平台连接，球铰(S副)与动平台连接，P副轴线通过S副中心点和R 副中心点且垂直于R 副转轴。在4 条支链的P副驱动下，配备在动平台上的打印头具有2个转动自由度和1个移动自由度(2R1T)。

并联机构的打印行程和打印空间一般会受到其结构的限制，使得大尺寸产品的打印受限，为此，本文引入如图3所示的十字运动平台来克服并联机构在xy方向运动的不足，进而增大3D打印的运动范围。十字运动平台主要由x方向移动平台组件、y方向移动平台组件和打印托盘组成。打印托盘安装于x方向移动平台组件沿直线导轨方向移动(1T)，再由y方向移动平台组件实现垂直方向直线导轨的移动(1T)，至此，打印托盘具有2个垂直方向的移动自由度。

图3 十字运动平台虚拟样机模型Fig.3 Virtual prototype model of the cross motion platform

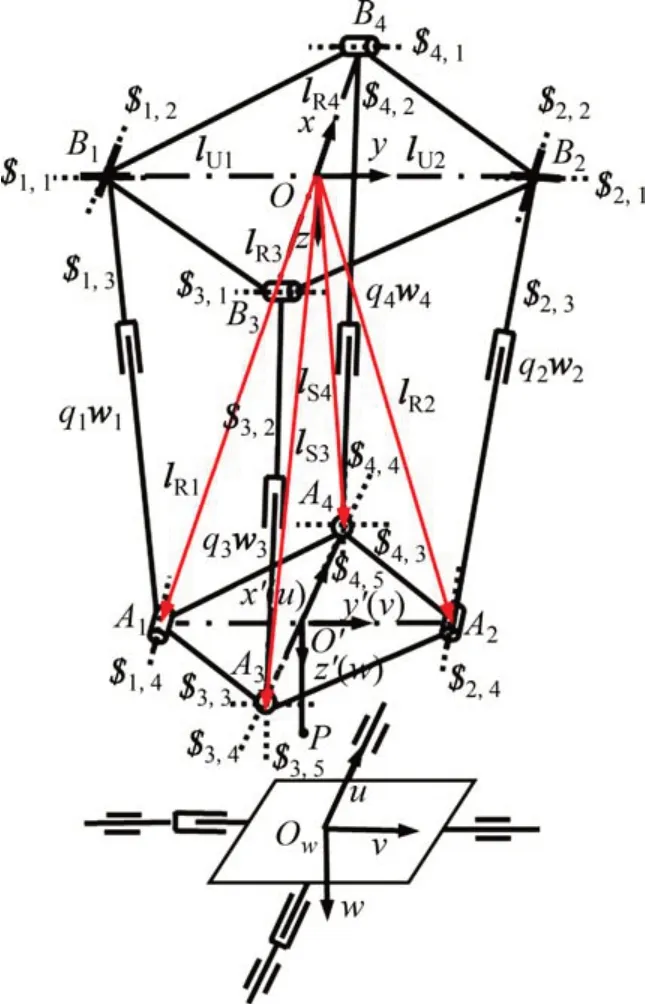
图4 混联3D打印机构简图Fig.4 Schematic diagram of the 5-DOF hybrid 3D printer

混联3D 打印机的机构简图如图4所示。图4中，点Ai(i=1～4)为支链i与动平台连接的运动副几何中心点，点Bi为支链i与定平台连接的运动副几何中心点。为便于分析，记$i,j为支链i的第j(j=1～5)个运动副的单位向量，为支链i对动平台的第j个约束螺旋。为便于得到运动旋量，分别在并联机构的静平台几何中心O、动平台几何中心点O′和打印托盘几何中心点Ow上分别建立全局坐标系Oxyz、动坐标系O′x′y′z′和Owuvw。其中，Oxyz坐标系的x轴与B3B4共线且同向，z轴垂直于静平台向下，y轴满足右手定则；O′x′y′z′坐标系的x′轴与A3A4共线且同向，z′垂直于动平台向下，y′轴满足右手定则；Owuvw坐标系的u轴、v轴和w轴分别与Oxyz坐标系的各轴平行且同向；定平台和动平台的外接圆半径分别为b和a；qi和wi分别为支链i的移动副长度和移动副方向的单位向量。另外，在动平台中心点建立瞬时坐标系O′uvw，且3 个正交轴分别平行于全局坐标系的3个正交轴。

2 运动学分析

2.1 自由度分析

为实现既定运动自由度，设定图4所示并联机构中各运动副的单位向量满足如下约束条件：

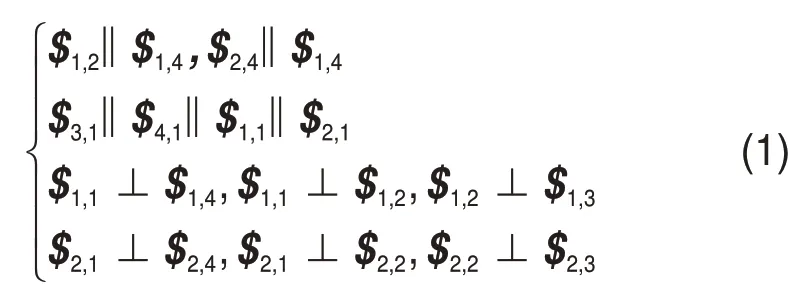
在任意位姿下，支链1的运动螺旋系可表示为

式中：lU1和lR1为第1支链U副和R副的几何中心点在全局坐标系下的位置向量。

对式(2)求反螺旋得

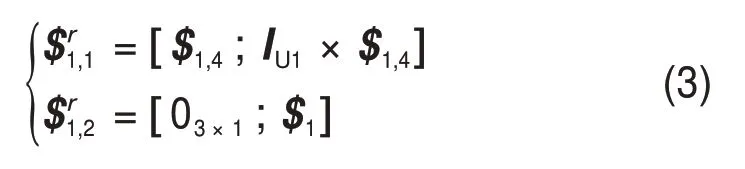
式中：$1为单位方向向量

同理，可得到支链2的运动螺旋系，再通过反螺旋运算得到约束螺旋系为

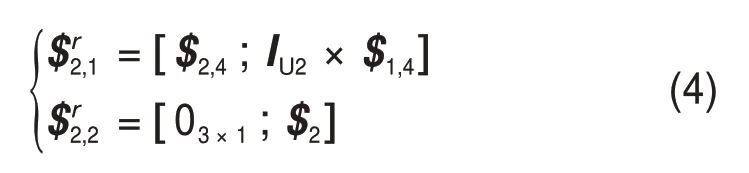
式中：lU2为第2支链上U副的几何中心在全局坐标系下的位置向量；$2为单位方向向量($2,1×$2,2)/|$2,1×$2,2|。

支链3的运动螺旋系为

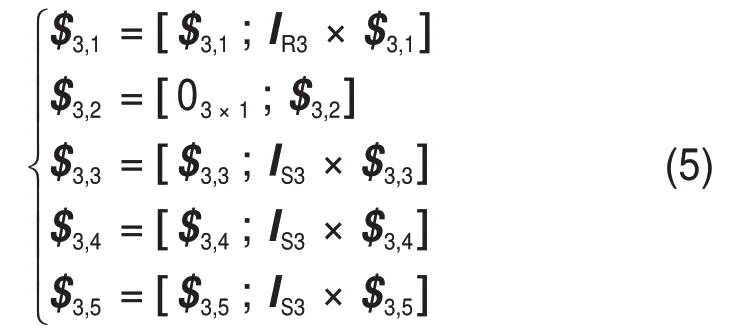
式中：lR3和lS3分别为第3支链R和S副几何中心点在全局坐标系下的位置向量。

对式(5)求反螺旋得

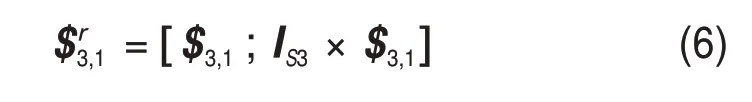
同理，可得到支链4的运动螺旋系，再通过反螺旋运算得到约束螺旋系为

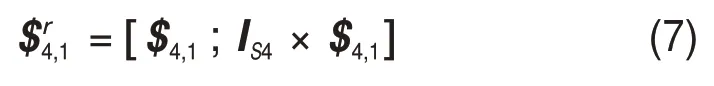
4 个支链施加给动平台的6 个约束螺旋，即为并联机构动平台的约束螺旋系。对上述约束螺旋系求反螺旋可得到并联模块动平台的运动螺旋系：

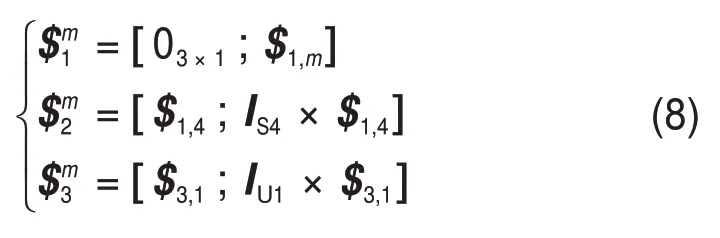
结构相对简单的十字运动平台由2个相互垂直的直线运动导轨组成，进而可以实现沿x轴和y轴方向的移动自由度。至此，可知该3D打印机具有5个自由度(2R3T)。

2.2 运动学逆解

打印机的运动学逆解过程如下：已知动平台上打印头末端点P相对于打印托盘上的Owuvw坐标系的位置和姿态，计算并联机构各支链移动副的长度qi(i=1～4)和打印托盘中心点Ow在全局坐标系x轴和y轴上的位置(即十字运动平台的位置)。

为求解该打印机的混联逆解，将其分解为2个闭环矢量链，分别为：定平台→十字运动平台→打印产品的定平台→打印产品的闭环矢量链L；定平台→2UPR&2RPS支链→动平台→打印头的定平台→打印头末端点的闭环矢量链N。

动平台坐标系Ox′y′z′相对于全局坐标系Oxyz的姿态旋转变换矩阵可表示为

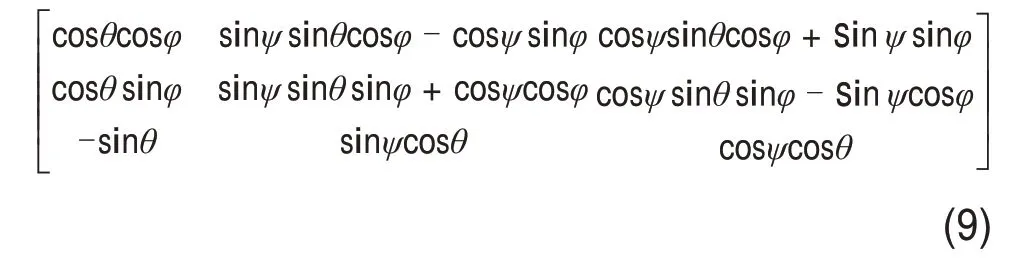
式中：φ，θ和ψ分别为O′x′y′z′相对于Oxyz的3 个姿态角。

在全局坐标系Oxyz下，动平台O′点位置矢量、向量si,1和si,4(i=1,2)及sj,1(j=3,4)可表示为

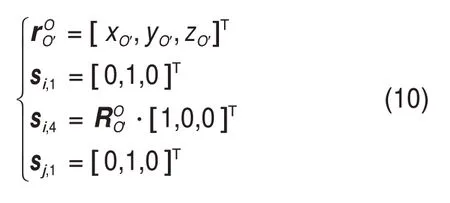
结合式(1)，可得如下约束条件：

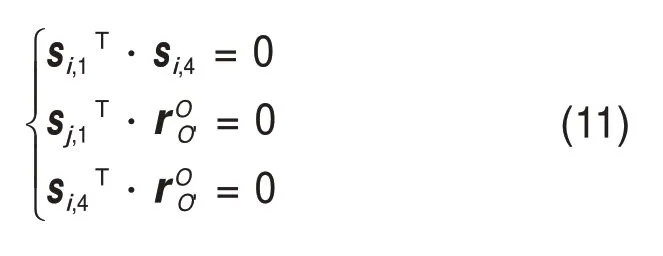
将式(10)代入(11)可得到

至此，并联机构的位姿由zO′，θ和ψ这3 个参数确定。

打印头轴线与O′uvw的w轴重合，可得打印头轴线的方向矢量为

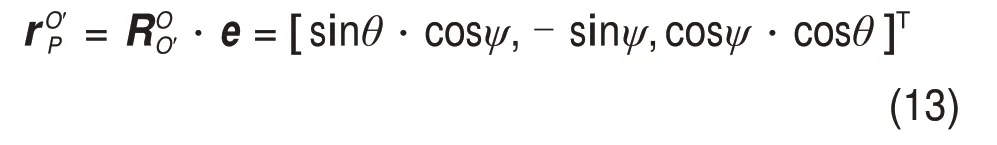
式中：e=[0 0 1]T。

由闭环矢量链N可得打印头末端点P在全局坐标系Oxyz的位置矢量可表示为

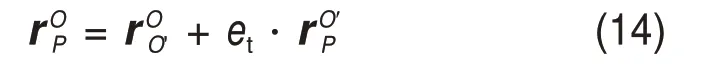
式中：et为打印头末端点P到点O′的距离；=[xP,yP,zP]T。

由于Owuvw坐标系相对于Oxyz坐标系各轴同向且平行，故Owuvw坐标系相对于Oxyz坐标系的旋转矩阵可表示为

式中：I3为三阶单位矩阵。

设打印头末端点P在Owuvw坐标系下位置矢量为姿态角为ψP，φP和θP，打印头固定在动平台上且轴线与O′x′y′z′的z′轴重合，因而，打印头的姿态角与动平台姿态角在运动过程中保持一致，即

由闭环矢量链L可得，打印头末端点P位置矢量在全局坐标系下又可表示为

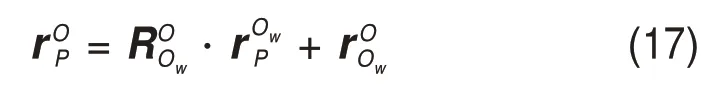
式中：=[xw,yw,zw]T，为Ow在全局坐标系下的位置矢量。

将式(14)和式(17)相减可得

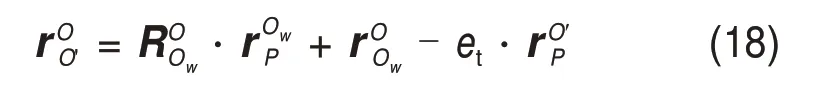
在闭环矢量链N 中，由闭环矢量回路法，可得到并联机构闭环矢量方程：

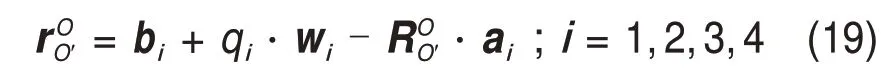
式中：bi和ai分别表示从O到Bi和点O′到Ai的位置矢量。

Bi和Ai在相应坐标系下的相对位置表示为

式中：βi和αi分别为位置矢量ai和bi与x轴和x′轴的夹角，βi=αi=(-1)i·π/2；i=1,2；βi=αi，αi=π·(i-2)；i=3,4。

通过联立式(18)和式(19)可求得运动学逆解为

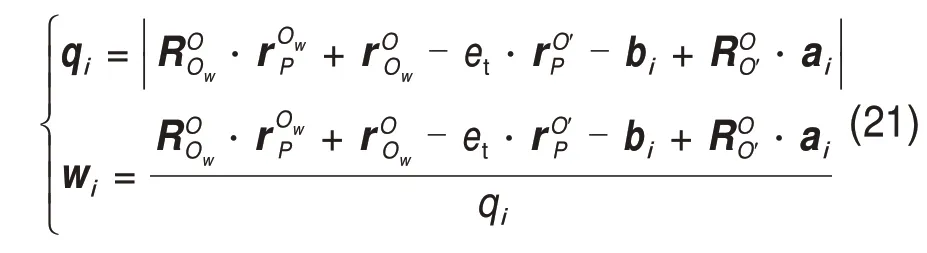
式中：i=1,2,3,4。

打印托盘原点Ow在全局坐标系x轴和y轴的移动靠十字运动平台实现，坐标xw和yw即为十字运动平台的位置。

已知打印头末端点P在Owuvw下的位置和姿态，结合式(12)～(14)和式(18)化简得到十字运动平台的位置为

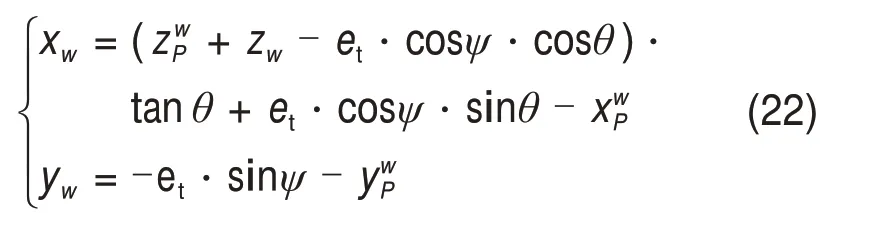
2.3 运动学正解

通过式(21)可求得

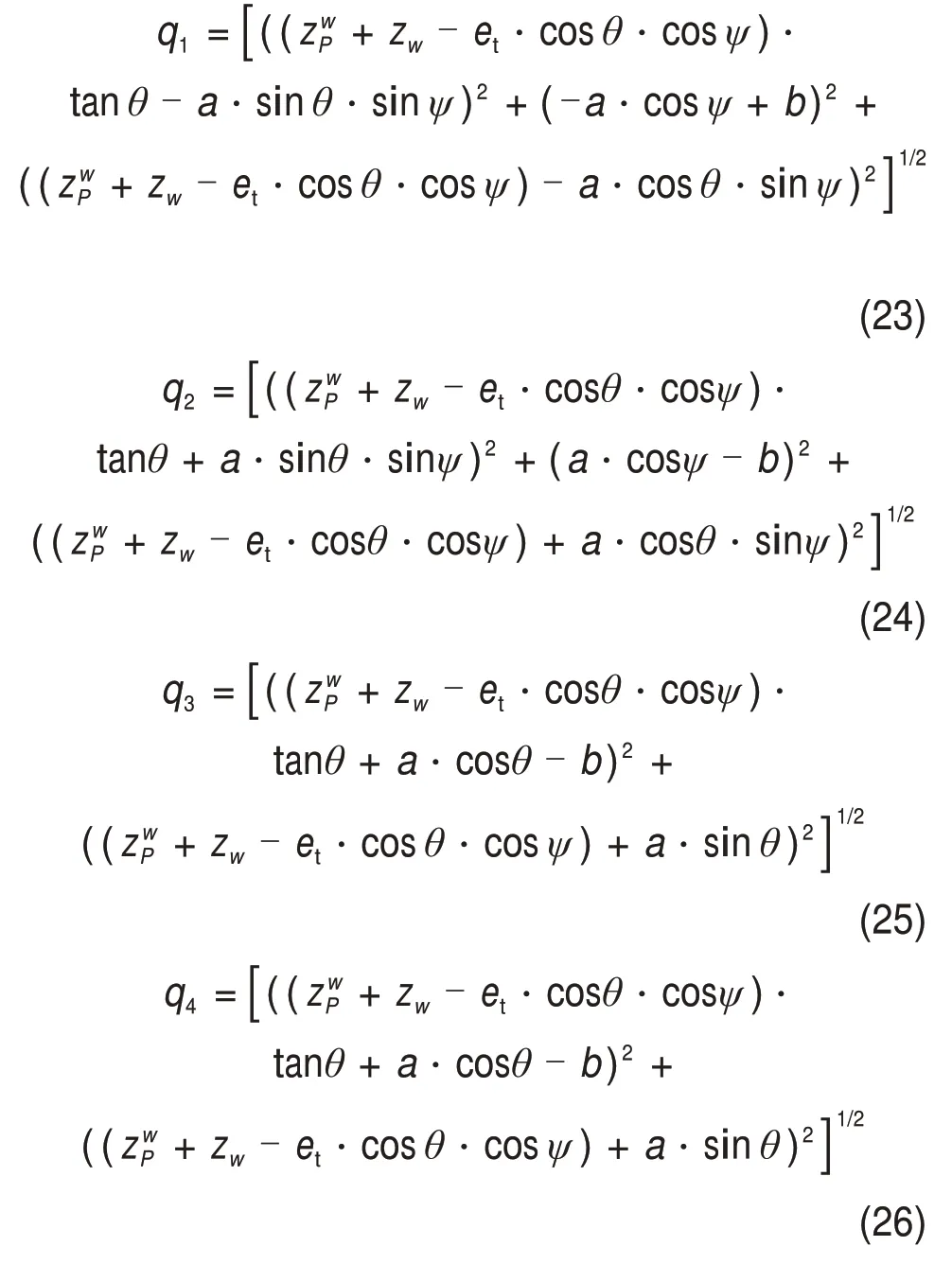
由式(23)～(26)可得关于cosθ的一元三次方程

为求解式(27)，令cosθ=t0i，代入式(27)可得到方程的3个根：

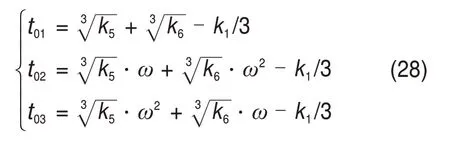
根据式(1)的约束条件可知θ∈[-π 2,π 2 ]，则t0i∈[0,1]，又3个根中只有实根且满足t0i∈[0,1]才能得到θ，因而，可通过判断t0i是否在区间内来确定θ。

又由于θ的符号与q4-q3的差值相关，则可得

将式(29)代入式(23)～(26)，联立可得：

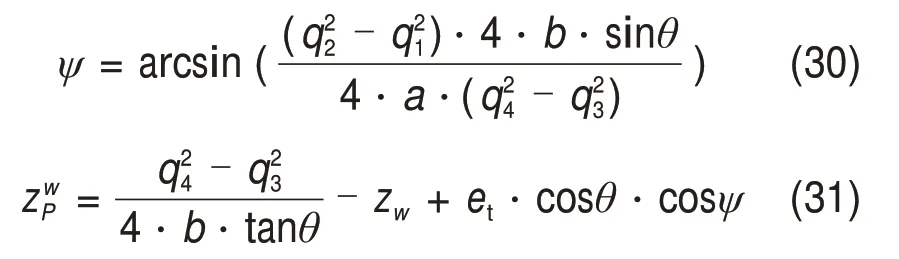
将式(29)～(31)代入式(22)可得

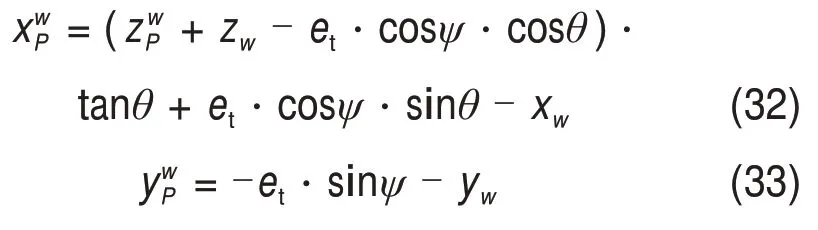
3 工作空间预估

工作空间预估是判断打印头作业时，所能达到最大范围的重要指标。下面采用分层切片的搜索思想，建立打印机在打印托盘Owuvw坐标系下的姿态工作空间和位置工作空间。由于移动副行程和运动副转角的限制，打印装备的工作空间就需要考虑二者约束的交集，其约束条件描述如下。

1)各支链i的移动副长度和十字运动平台移动行程约束条件为

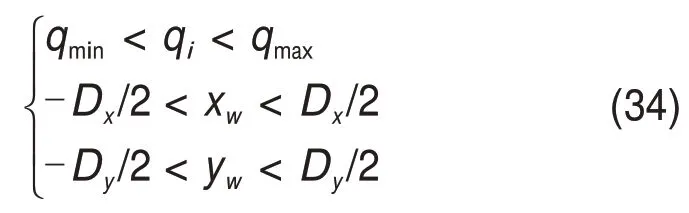
式中：qmin和qmax分别为支链i的最小和最大移动副长度；Dx和Dy分别为十字运动平台分别为沿x方向和y方向的直线移动行程极限(在全局坐标系下度量)。

2)并联机构中R，U和S副的转角约束条件分别如下。

转动副R的转角为

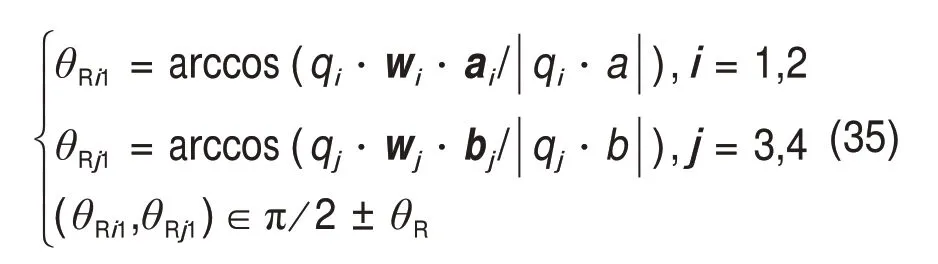
式中：θRi1为支链i(i=1,2)的转动副转角；θRj1为支链j(j=3,4)的转动副转角；θR为转动副的极限转角。

虎克铰U的转动角度为

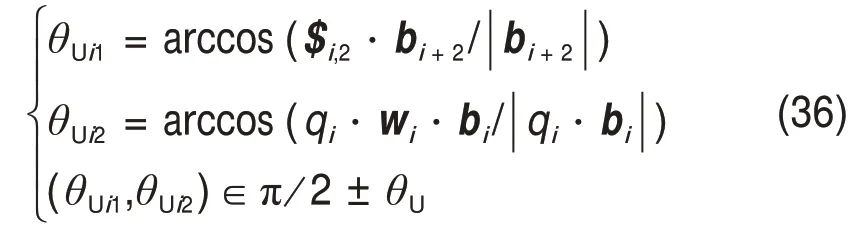
式中：θUi1和θUi2分别为支链i的虎克铰两交叉轴的转角；θU为虎克铰的极限转角。

球铰S的转动角度为

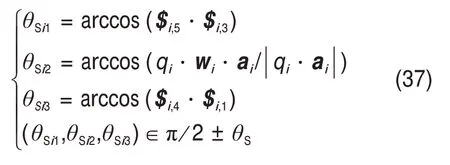
式中：θSi1，θSi2和θSi3分别为球铰的3个交叉轴的转角；θS为极限转角。

该3D打印机工作空间的搜索流程如图5所示。

根据图5可知打印机工作空间搜索步骤如下。

1)在Owuvw坐标系下，以(Δw，Δψ，Δθ)为增量建立姿态空间(w，ψ，θ)；以(Δw，Δu，Δv)为增量建立位置空间(w，u，v)。

2)根据逆运动学求解相关变量，通过各支链移动副长度、十字运动平台极限行程、U 副、S副、R副等转角约束条件来判定离散点是否在其工作空间内。

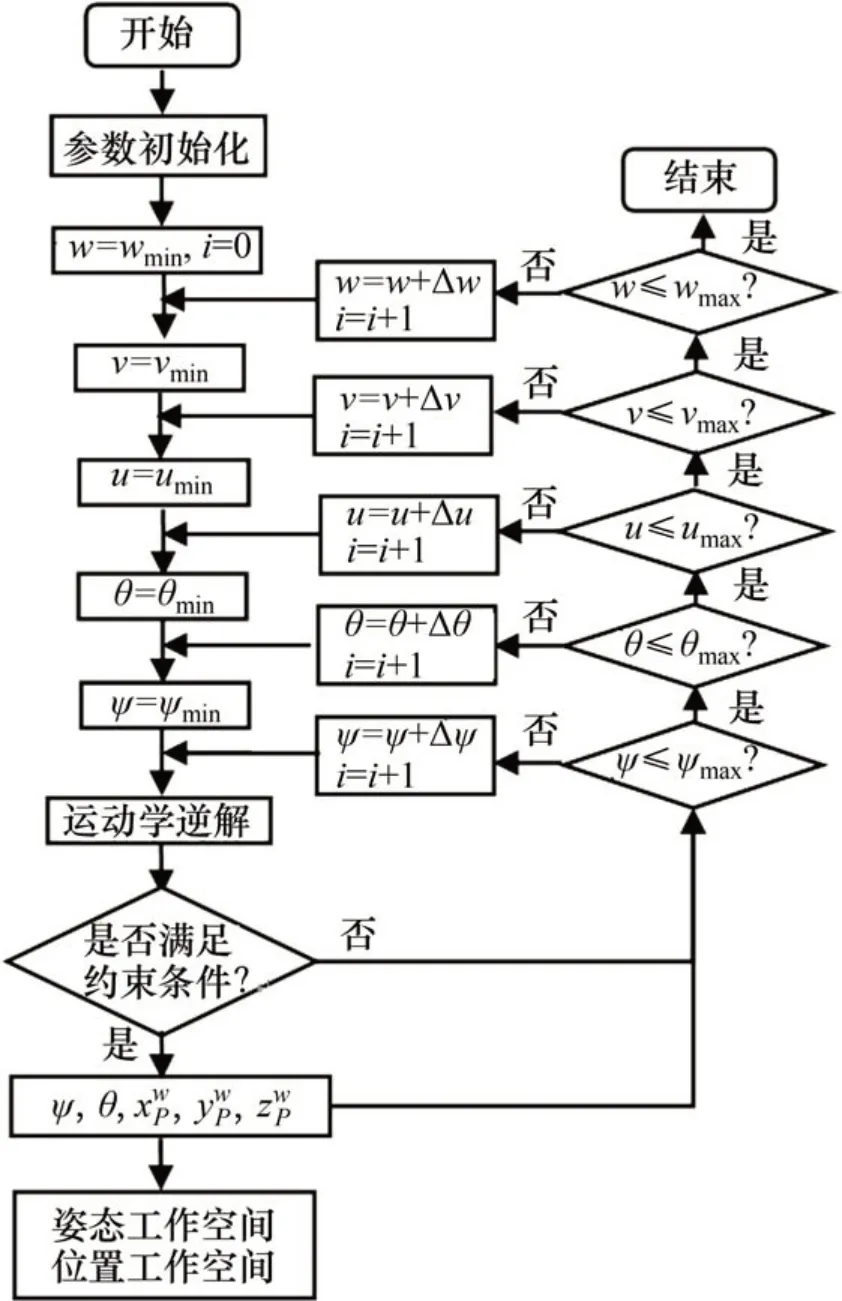
图5 工作空间搜索流程Fig.5 Flowchart of workspace researching

3)将满足约束条件的可行点记录并分别绘制成打印装备的姿态工作空间以及位置工作空间。

以图1所示的混联3D 打印机为例，运用上述方法预估其工作空间，其几何及结构参数如表1所示。

表1 混联3D打印机的几何及结构参数Table 1 Geometric and structual parameters of the hybrid 3D printer

经工作空间搜索流程得到3D 打印机在打印托盘Owuvw坐标系下的姿态工作空间和位置工作空间，分别如图6(a)和6(b)所示。经分析可知，打印机具有姿态工作空间体积为0.12 m·rad2，位置工作空间体积为0.004 6 m3，且均为对称分布的多面体。姿态工作空间在w=-76 mm 处有最大的截面，如图7(a)所示；沿ψ轴和θ轴的最大工作截面分别在ψ=0°和θ=0°处，如图7(b)和7(c)所示。类似地，位置工作空间沿u，v和w轴的最大工作截面在u=0 mm，v=0 mm和w=-76 mm，如图8所示。

由图7(a)可知，打印头的ψ和θ最大转角范围分别为[-30°,30°]和[-35°,35°]；由图7(b)和7(c)可知打印头沿w轴方向的移动范围为[-150,0]mm且截面呈对称分布，这与打印机的2条UPR 支链和2 条RPS 对称布置机构特点相对应.类似地，由图8可知打印头末端点P位置范围u∈[-230,230]mm，v∈[-150,150]mm 和w∈[-150,0]mm。根据上述分析，该打印机在打印作业时，产品在长×宽×高为200 mm×300 mm×150 mm内为最佳范围，且距离打印托盘表面高度w为[-75,-125]mm能达到最大的转动角度，实现多向3D打印。

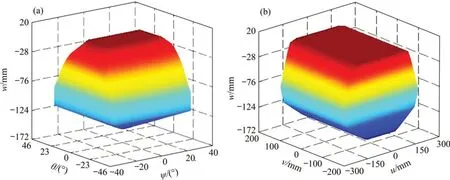
图6 工作空间示意图Fig.6 Schematic diagram of workspace

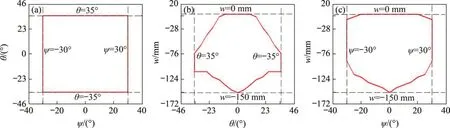
图7 姿态工作空间截面图Fig.7 Cross section of orientation workspace

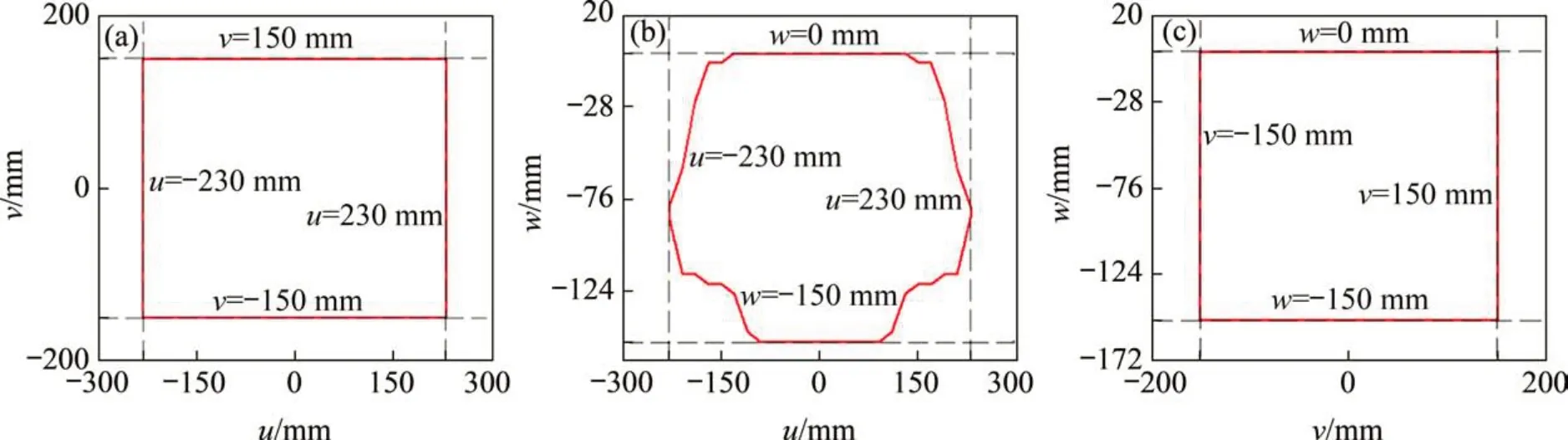
图8 位置工作空间截面图Fig.8 Cross section of position workspace

4 奇异性分析

混联3D 打印机中，十字运动平台不存在奇异位置，因而，确定主体模块并联机构的奇异位置是避免打印作业过程中出现运动突变的关键。

在瞬时坐标系O′uvw下，设动平台O′点处的线速度为vO′，动平台的角速度为ωO′，则动平台上Ai点的线速度vAi可表示为

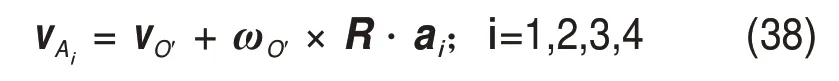
则4个驱动副的线速度Vqi为

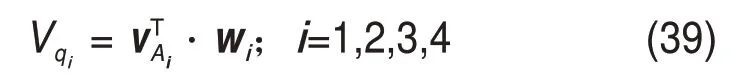
将式(38)代入式(39)可得到

定平台上点Bi的线速度vBi在瞬时坐标系O′uvw下可表示为

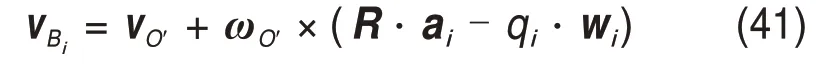
对于2 条UPR 支链，具有过虎克铰中心点Bi(i=1,2)且平行于$i,4(i=1,2)的约束力，2 条RPS支链具有过球铰几何中心Ai(i=3,4)且平行于$i,1(i=3,4)的约束力，则点Bi(i=1,2)沿$i,4方向以及Ai(i=3,4)沿$i,1方向的运动受到约束。

因此，对式(38)和式(41)分别乘以$i,1和$i,4，可得

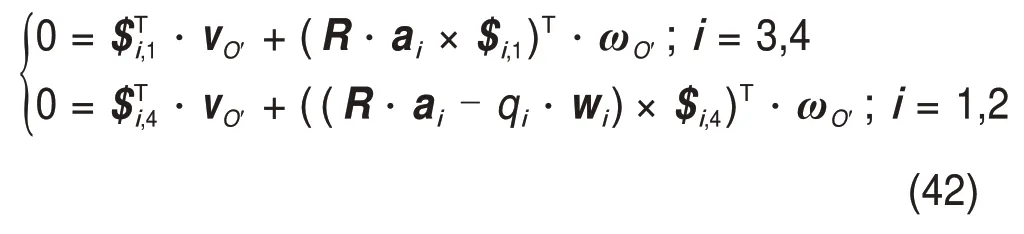
另外，2 条UPR 支链均具有一个垂直于$i,1和$i,2(i=1,2)的约束力偶，则动平台绕轴线$i,1×$i,2(i=1,2)的转动受到约束，有

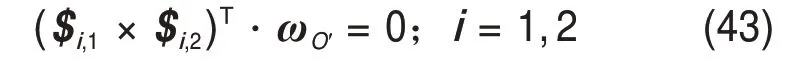
结合式(42)和式(43)，可得：

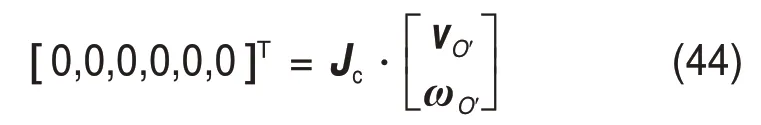
根据2 条UPR 支链产生的约束力和约束力偶相等以及2条RPS支链产生的约束力也相等，则除去约束雅克比相等的行数，得到约束雅克比矩阵最大的线性无关矩阵J′c：

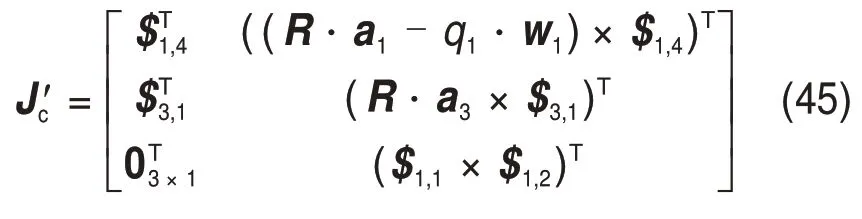
将式(40)和式(44)进行合并，可构造并联机构的全雅克比矩阵J：

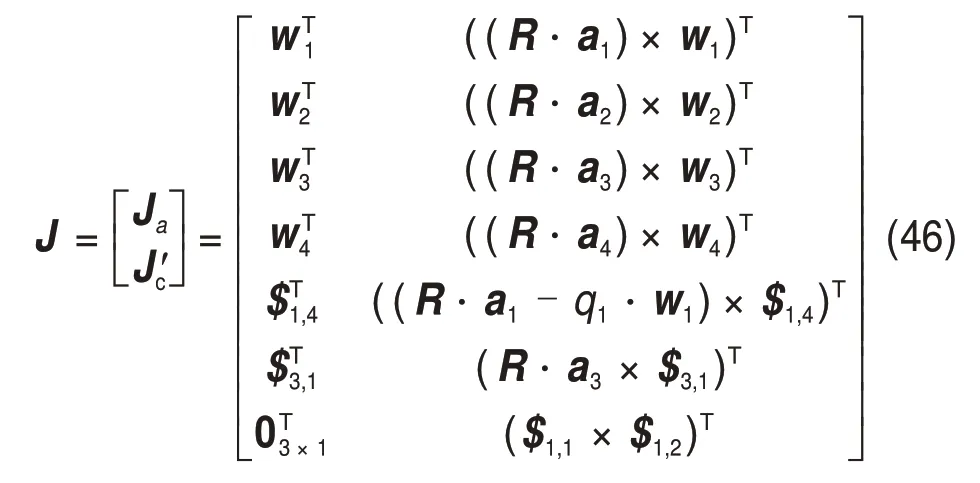
在一般情况下，奇异分为2种情况即机构奇异和约束奇异。若约束雅克比矩阵的秩小于6-f(f为自由度数)，则并联机构存在约束奇异。若驱动雅克比矩阵的秩小于f或者全雅克比矩阵的秩小于6且驱动雅克比矩阵的秩为f，则并联机构存在结构奇异。很显然，由式(1)的几何约束关系，约束雅克比矩阵J′c的3行均呈线性不相关，不会出现约束奇异。

若驱动雅克比矩阵Ja的秩小于3，即出现支链轴线方向矢量wi(i=1～4)相互平行/共面，如图9所示，则3D打印机的并联机构出现结构奇异。

图9 并联机构奇异位置Fig.9 Singular position of parallel manipulator

若式(46)的全雅克比矩阵J的秩小于6 并且驱动雅克比矩阵的秩为3，即2条UPR支链与动平台平行时，如图10所示，则3D打印的并联机构出现机构奇异。

据上述分析得到该并联机构存在结构奇异，不存在约束奇异。而上述结构奇异位置超出关节转角的约束范围，故可以判断，在3D打印作业的工作范围内不存在奇异位置，即避免了打印过程中出现运动突变的现象。

图10 并联机构奇异位置Fig.10 Singular position of parallel manipulator

5 运动仿真与验证

为了验证所提3D 打印机设计的可行性以及运动学理论的正确性，采用SolidWorks 软件对其进行运动仿真验证。为不失一般性，在可达工作空间内选择3个在Owuvw坐标系下的典型位姿进行仿真，如表2所示。

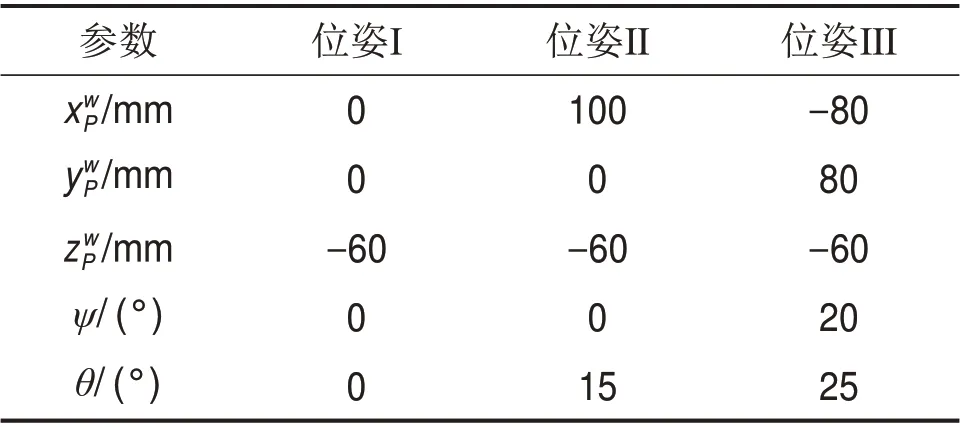
表2 在工作空间内的典型位姿Table 2 Typical poses within workspace

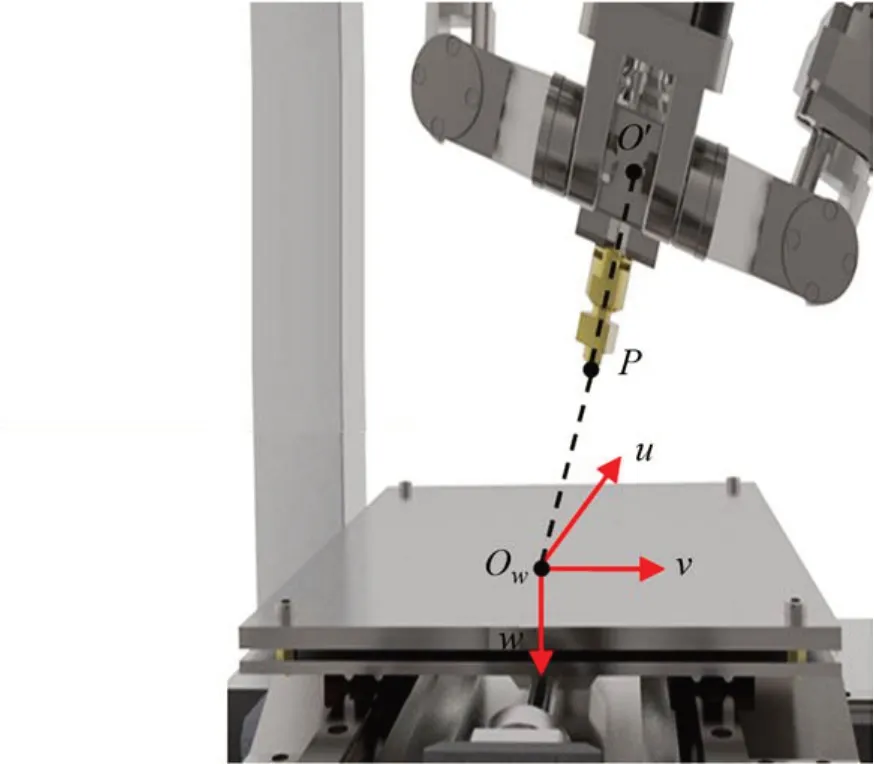
图11 在SolidWorks软件中测量点的位置坐标Fig.11 Position vector of measured point in the SolidWorks software

混联3D 打印机的仿真验证流程如图12所示，可概括如下。

图12 运动仿真验证流程Fig.12 Verification flow of motion simulation

1)从表2中选择所设定的典型位姿，将位姿代入运动学逆解方程，求得并联机构各支链的移动副长度qi和十字运动平台在Oxyz坐标系下的位置xw和yw。

2)将上述qi，xw和yw通过SolidWorks软件代入混联3D打印机的虚拟样机上并建立打印托盘坐标系Owuvw，如图11所示。借助SolidWorks 测量功能，测得点P和O'在坐标系Owuvw下的坐标。为表示打印头的姿态，采用打印头轴线的方向矢量表示其姿态，由软件可测量方向矢量(上标“m”表示在SolidWorks 中测量得到)和打印头末端点P的位置矢量。

3)将在步骤1)选定位姿下得到的qi，xw和yw代入Matlab编写的运动学程序，可以得到理论的点P位置矢量(上标“T”表示在Matlab 中计算得到)和理论的打印头方向矢量.

4)根据步骤2)仿真测得的点P位置矢量和打印头方向矢量的结果与步骤3)理论计算结果，可分别求得P在系O′x′y′z′和系Owuvw下的位置矢量误差和方向矢量误差。

5)返回步骤1)，选择另一个测量位姿，重复步骤2)～4)。

由SolidWorks 软件仿真测得的位置矢量与方向矢量和Matlab计算结果如表3所示，位置矢量与方向矢量的误差为零，可证实所设计的3D打印装备的可行性和运动学理论推导的正确性。

表3 运动仿真验证结果Table 3 Verification results of motion simulation

6 结论

1)提出了一种由拓扑构型为2UPR&2RPS的并联模块和具有2个自由度的十字运动平台组成的具有5个自由度的混联3D打印机。该混联3D打印机在实现xyz三轴运动的同时，通过θ和ψ转角可实现多向3D打印。

2)基于旋量理论的分析可知该混联3D打印机具有两转动和三平动的运动能力(2R3T)。由闭环矢量回路法得到了混联打印机运动学逆解，再由逆解方程推导出运动学正解方程。

3)利用分层搜索的思想，得到了混联3D打印机的位置工作空间和姿态工作空间，并对其进行奇异性分析，结果表明该混联机器人不仅能实现三平动的分层打印，而且能够通过改变打印头的姿态实现多向3D 打印且在工作空间内无奇异位置。

4)利用SolidWorks 软件仿真和Matlab 编写的运动学程序进行对比和分析，证实混联3D打印机设计的可行性和运动学理论推导的正确性。