液驱并联机构多维力加载系统CMAC-模糊PID控制

赵劲松，王春发，徐嘉祥，董杰，孙鑫宇，赵子宁

(1.燕山大学河北省重型机械流体动力传输与控制实验室，河北秦皇岛，066004；2.浙江大学流体动力与机电系统国家重点实验室，浙江杭州，310027；3.燕山大学机械工程系，河北秦皇岛，066004)

为保证航天器空间对接机构、数控机床主轴、大型客机机翼翼肋等受力复杂构件的可靠性，需要对构件进行多维力加载实验[1-2]。以Stewart 平台为基础的液驱并联机构多维力加载系统体积小、刚度大、承载能力强，且能够实现多维力/力矩加载，是多维力加载实验的重要设备[3-4]。然而，受系统自身结构与参数摄动等非线性因素影响，液驱并联机构多维力加载系统具有很强的非线性、时变和强耦合性，给系统控制带来了很大困难，因此，进行高精度的控制策略的设计研究具有重要意义[5]。液驱并联机构多维力加载系统控制策略可以从2个框架进行设计：一种是基于工作空间设计，另一种是基于关节空间设计[6-7]。基于工作空间的控制器设计将系统动力学模型纳入力闭环控制的前向通道中，增加了系统的非线性。基于关节空间的控制器设计中每个液压动力单元都可看作独立的力闭环，上平台广义力指令通过雅克比转置逆矩阵计算出各关节液压缸力，与各关节液压缸的拉压力传感器采集的实际力构成液压缸力闭环控制，简化了控制器设计任务。基于关节空间的控制器设计是液驱并联机构多维力加载系统控制的热点研究领域。武锡铜等[8]为实现Stewart平台的高精度运动控制，在关节空间中设计了位置-速度双环控制器，使用分段积分重置PI 控制器作为位置环控制器，加快系统镇定速度，采用自抗扰控制器作为速度控制器抑制扰动。LIU 等[9]提出了一种考虑关节耦合的并联机器人前馈控制器参数整定的迭代方法，通过最小化每一步关节跟踪误差的平方和，迭代更新前馈调谐参数的增量，使联轴器跟踪误差的均方根减少了22%。TAGHIZADEH等[10]提出了一种液驱Stewart并联机器人神经网络自整定NN-PID控制方案，通过反向传播算法对神经网络进行在线训练，使期望值与实际输出误差最小化，提高了系统的鲁棒性。PID控制具有原理简单、使用方便等特点，在现代工业机器人中应用广泛，结合智能控制算法设计先进的PID 控制器，对非线性系统控制具有重要意义。利用模糊控制鲁棒性好和适应性强的优点，对PID 控制参数进行实时调整，构成模糊PID 控制，提高了传统PID 控制在非线性系统中的有效性。樊锐等[11]将模糊PID控制策略应用于6-PUS并联加载机构单支链力控控制器中，明显降低了响应力超调量，但实现高精度系统控制需要精确的模糊逻辑规则，依靠经验与试凑法完善控制规则的过程较复杂。小脑模型神经网络控制器(CMAC)具有学习时间短、实时性强、结构简单、响应速度快的优点，具有较强的逼近非线性映射的能力。岳学磊等[12]将CMAC-PID 控制器应用到无刷直流电机控制系统中，提高了控制系统的响应速度与抗干扰能力，但为保证系统控制精度，CMAC 需要进行大量的离线训练。LIAO 等[13]通过层次聚类技术确定CMAC 每个权值表的标签数，平衡CMAC泛化能力与精度，提高了内存分配的效率。CMAC与模糊PID并行的控制策略将模糊PID的输入输出作为样本，对CMAC 进行训练，逐渐消减了模糊PID控制权重，可实现高精度实时多维力加载控制。邢立新等[14]将CMAC与模糊PID并行的控制策略应用到火炮调平控制系统，验证了CMAC-模糊PID复合控制的有效性。考虑到并联机构多维力加载系统结构的特殊性，将CMAC-模糊PID 复合控制应用到多维力加载系统中。为了提高液驱并联机构多维力加载系统控制精度，本文作者建立液驱并联机构多维力加载系统数学模型，分析耦合机理，设计复合控制器，通过对比PID 控制、模糊PID 控制与CMAC-模糊PID 复合控制加载实验结果，验证CMAC-模糊PID 复合控制在非线性系统中的有效性，以期为液驱并联机构多维力加载系统控制提供新思路。

1 多维力加载系统建模

液驱并联机构多维力加载系统采用Stewart 平台为基本结构，上平台与下平台通过胡克铰、伺服作动器连接，如图1所示。图1中，Ai为第i个上铰点在动坐标系中的坐标矢量，Bi为第i个下铰点在惯性坐标系中的坐标矢量。工作时，伺服作动器伸缩变化，输出力和位移，通过胡克铰将这种变化传递到上平台，可实现上平台广义空间六自由度力/力矩加载。

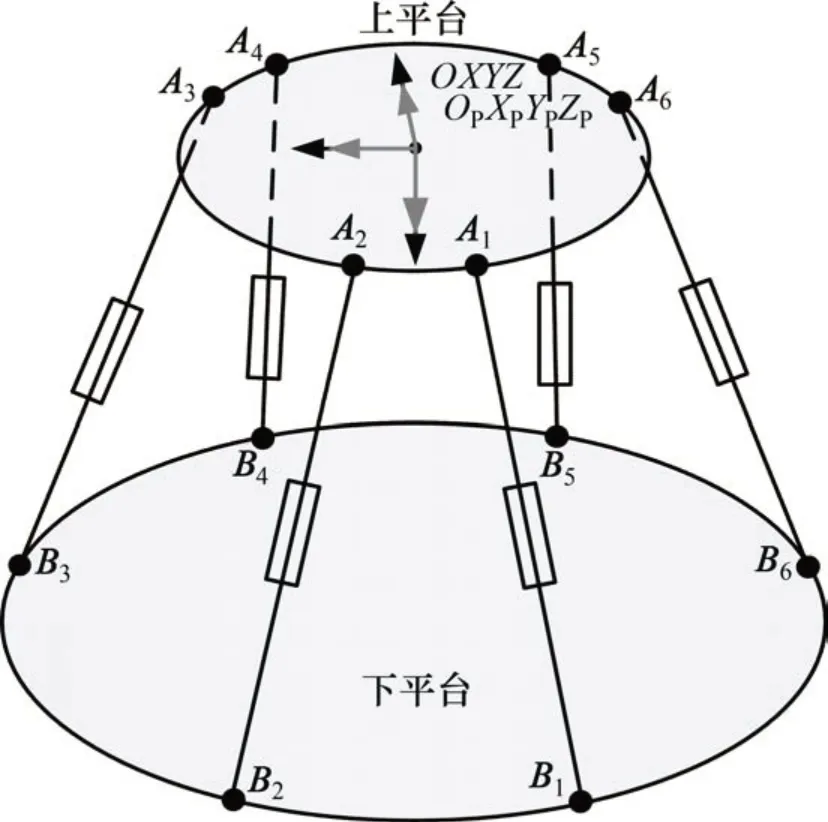
图1 Stewart平台结构简图Fig.1 Diagram of stewart platform structure

Stewart 平台通道间存在严重的交联耦合，是典型的非线性系统，主动力加载的建模过程见文献[15]。本文在系统动力学模型的基础上，对系统耦合力产生的机理进行分析。

在上平台中心建立动坐标系OPXPYPZP，动坐标系与上平台固连在一起，跟随上平台一块运动。当上平台处于初始中心位置时，动坐标系OPXPYPZP与惯性坐标系OXYZ重合。

上平台力平衡方程为

式中：Ln为各液压缸组成的单位向量矩阵；Fq为六通道活塞杆输出力向量矩阵；mA为上平台质量，为上平台加速度；g为重力加速度向量；F′为上平台所受外力。

上平台力矩平衡方程为

式中：T为动坐标系与惯性坐标系之间旋转变换矩阵；A为上平台各铰点在动坐标中的坐标矩阵；IA为上平台转动惯量矩阵；ω为上平台在惯性坐标系下角速度；M′为上平台与被试工件间相互作用力矩。

考虑到每个通道活塞杆和缸筒的重力、惯性力和惯性力矩，将这些力或力矩在上平台广义速度方向和广义加速度方向投影，可得整个并联机构的动力学方程为

式中：JF为并联机构力雅可比矩阵；Mc为广义质量矩阵；Cc为科式向心项系数矩阵；Gc为重力项矩阵；F为系统输出的广义力矩阵。

当系统的广义质量阵Mc为对角阵时，

此时，各力加载通道间不存在耦合力/力矩，但受系统自身结构与液压系统参数摄动等非线性影响，广义质量矩阵Mc为非对角阵，在进行多维力加载时，系统存在惯性力交联耦合，影响力加载精度[16]。

2 液压动力元件建模

多维力加载系统动力元件采用伺服阀控制非对称缸，其单通道力控系统由控制器、伺服阀、液压缸，拉压力传感器组成，其原理图如图2所示。

图2 单通道力控系统原理图Fig.2 Schematic diagram of single channel force control system

采用机理建模方法构建伺服阀控非对称缸数学模型，其详细的建模过程见文献[17]。阀控非对称缸液压系统原理图如图3所示。图3中，Ps为供油压力，P0为回油压力，A1和A2分别为无杆腔、有杆腔活塞杆有效面积，P1和P2分别为无杆腔、有杆腔油液压力，q1和q2分别为无杆腔、有杆腔流量，Cip为液压缸内泄系数，Cep为液压缸外泄系数，Bp为黏性阻尼系数，K为负载刚度。设阀芯位移为Xv，液压缸位移为X。

图3 阀控非对称缸原理Fig.3 Schematic diagram of valve controlled asymmetric cylinder

定义负载压力PL为

式中：η为非对称缸受力面积之比，η=A2/A1。

定义负载流量qL为

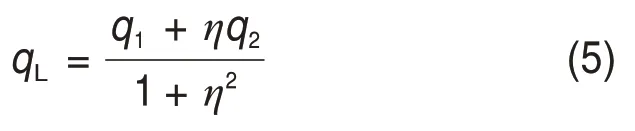
伺服阀流量方程、液压缸流量方程、液压缸力平衡方程拉式变换为

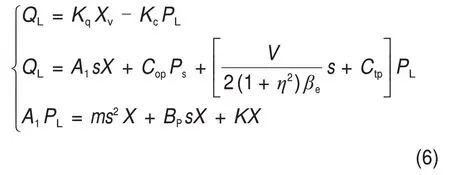
式中：Kq为流量增益系数；Kc为流量压力系数；Ctp为油缸综合泄漏系数；Cop为系统等效泄漏系数；s为拉普拉斯微分算子；βe为液压油体积弹性模量；m为活塞杆及负载折算到活塞上的总质量；V为液压缸有效容积。

伺服阀控非对称缸正反向运动开环增益不同

式中：Kq1，Kc1和Cop1分别为活塞杆正向移动流量增益系数、流量压力系数、等效泄漏系数；Kq2，Kc2和Cop2分别为活塞杆反向移动流量增益系数、流量压力系数和等效泄漏系数。

忽略Cop1和Cop2，则阀控非对称缸系统基本方程可简化为

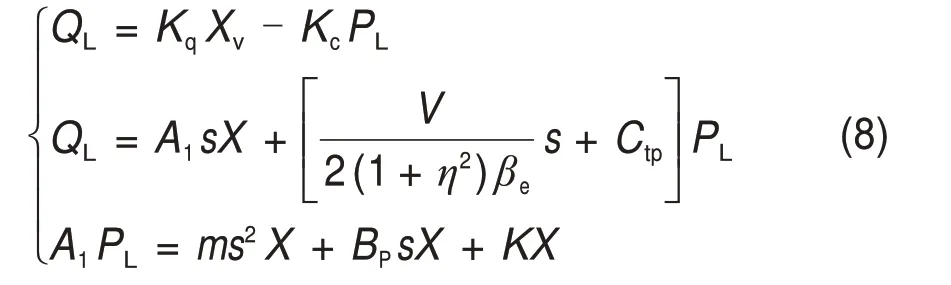
伺服阀阀芯位移Xv与活塞杆输出力Fq之间的传递函数为

式中：Kce为总流量-压力系数。

由于系统固有频率和伺服阀频宽相近，电液伺服阀在建模时可简化为二阶振荡环节[18]：

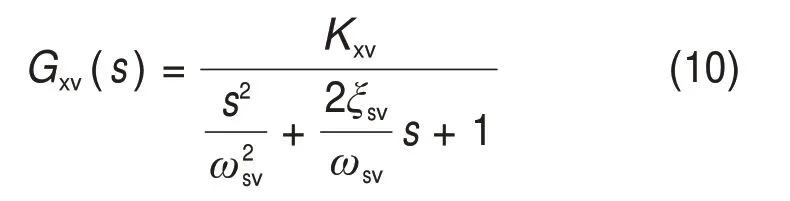
式中：Gxv(s)为伺服阀传递函数；Kxv为伺服阀增益系数；ωsv为伺服阀固有频率；ξsv为伺服阀阻尼比。

由于伺服放大器的频宽远高于系统液压固有频率，所以，可以将伺服放大器等效成为比例环节建模，可表示为

式中：Ka为伺服放大器增益系数；I(s)为伺服放大器电流输出；U(s)为伺服放大器电压输入。

通过上述建模过程可以得到单通道伺服阀控非对称液压缸力控系统传递函数示意图，如图4所示，其中，Gc(s)为关节空间控制器传递函数。

3 CMAC-模糊PID 复合控制器设计

3.1 模糊PID控制器设计

模糊控制是一种规则控制，将现场操作人员的控制经验或相关专家知识作为系统的调节规则。运用模糊控制对PID控制参数进行实时调整，能够降低干扰和参数变化对系统稳定性的影响，提高控制系统的灵活性。模糊PID控制结构原理图如图5所示。模糊PID整体调控过程如下：1)首先比较单通道液压缸力指令与拉压力传感器反馈信号，计算单通道输出力偏差e(t)和偏差变化率c(t)；2)将以上计算结果作为模糊控制输入，经模糊处理后输出PID 参数修正值ΔKp，ΔKi和ΔKd；3)将反馈偏差与模糊控制输出量共同传输至PID 控制器，经PID控制器处理后输出液压动力元件控制信号；4)液压动力元件根据控制信号调整输出力，拉压力传感器采集信号与力指令信号进行比较。重复以上步骤。

液驱并联机构多维力加载系统模糊PID控制器的设计步骤如下。

3.1.1 偏差信号模糊化

根据仿真经验，确定输入量E的模糊论域为[-500，500]，C的模糊论域为[-2 000，2 000]。输出量ΔKp的模糊论域为[-2，2]，ΔKi的模糊论域为[-0.2，0.2]，ΔKd的模糊论域为[-0.01，0.01]。将E，C，ΔKp，ΔKi和ΔKd模糊论域的连续变量划分为7 个离散点，划分后的模糊子集为{PB，PM，PS，ZO，NS，NM，NB}，对应{正大，正中，正小，零，负小，负中，负大}。

3.1.2 隶属度函数确定

在隶属度函数之中，三角函数与高斯函数因为其计算简单、占用空间内存小的优点，被广泛应用于工程领域。控制器在靠近系统稳态处的输出决定了模糊控制器的控制性能，在论域的中间位置选择三角函数，并对其参数进行调整，使其斜率满足高精度控制的要求，提高系统的逼近精度。在论域的边界选择高斯函数，其在隶属度为1的论域元素附近变化平缓，能够模拟人工智能活动的特点，在初始状态输入值较大时提高系统的响应速度。E，C，ΔKp，ΔKi和ΔKd基础隶属度函数如图6所示。

3.1.3 模糊规则制定

模糊控制器经模糊逻辑推理输出PID参数修正值，为提高液驱并联机构多维力加载系统力跟随性能，根据PID控制特性，设计PID控制参数调整原则，参考文献[18]，根据偏差e(t)和偏差变化率c(t)对PID 参数修正值ΔKp，ΔKi和ΔKd进行相应调整。

3.2 CMAC控制器设计

CMAC 是一种能够表达复杂非线性函数的表格查询型自适应神经网络，其收敛速度快、结构简单且占用内存小，其网格机构如图7所示。液驱并联机构多维力加载系统CMAC基本控制思路为：1)将单通道力指令进行量化，通过虚拟空间映射在存储空间找到对应的状态地址；2)在存储空间中找到该状态对应地址的权值，求和得到CMAC输出；3)对比CMAC 输出值与模糊PID 输出值，根据学习算法修改已激活存储单元权值，其设计过程参考文献[19-20]。

图4 单通道力控系统传递函数示意图Fig.4 Block diagram of transfer function of single-channel force-control system

图5 模糊PID控制结构原理图Fig.5 Schematic diagram of fuzzy PID control structure

图6 不同参数基础隶属度函数Fig.6 Basic membership functions of different parameters

输入值根据量化级数激活输入空间的量化子空间，如第i个输入量si∈[a,b]，可得输入向量S量化值为

式中：round 为取整函数，smin和smax分别为输入的最小值和最大值；M为量化级数。

映射到虚拟存储空间的输入向量RP为

式中：c为泛化参数。

输出空间输出值为实际储存空间存储单元权值w′的加和，输出值Fc(si)为

权值调整指标Z为

式中：z(t)为误差信号幅值；r(t)为给定信号幅值，y(t)为反馈信号幅值。

图7 CMAC网络结构示意图Fig.7 CMAC network structure diagram

由梯度下降法可知，网络权值调整公式为

式中：μ为学习效率，α为动量因子。

3.3 复合控制器设计

多维力加载系统关节空间复合控制器由PID控制器、模糊控制器和CMAC 控制器组成，复合控制结构图如图8所示。通过模糊控制器对PID控制器的控制参数进行实时调整，构成模糊PID 控制器，实现反馈控制，保障了系统的稳定性，同时能够有效降低系统超调量。利用CMAC 前馈控制实现被控对象的逆动态模型，根据力指令对控制信号进行超前的调整，提高系统响应的快速性。CMAC控制器与模糊PID控制器并行控制，提高了系统整体的控制性能。在初始阶段，使用模糊PID控制器对多维力加载系统进行力闭环控制，同时将单通道力指令信号与模糊PID控制器的输出信号作为CMAC 控制器的训练样本，调整CMAC 控制器的输出使其与总控制输出的差值减小。本研究中，控制系统的采样周期设置为2 ms，每经过1个采样周期，便将上一采样周期采集到的信号作为样本输入进行迭代，在力加载过程中对CMAC 各存储单元的权值进行修正。随着模糊PID控制器的输出样本不断增加，CMAC 控制器的控制精度不断提高，模糊PID 与CMAC 并行控制。CMAC 控制器的权重越来越大，最终完全由CMAC控制。

图8 CMAC-模糊PID控制结构Fig.8 CMAC-fuzzy PID control structure

4 实验分析

4.1 多维力加载实验方案

多维力加载实验台由机械结构、液压系统、控制系统3个部分组成，实验台加载部分结构如图9所示。

图9 实验台结构Fig.9 Physical structure of the test bench

多维力加载实验台机械结构的主体为Stewart平台，液压动力元件为伺服阀控非对称缸，油源为恒压源。控制系统采用基于Matlab/xPC Target的快速原型控制技术，其组成如图10所示。上位机是PC 机，下位机是工控机。在上位机中采用MATLAB/Simulink 软件编写控制程序并编译为C语言，通过以太网将上位机中编译的程序代码下载至下位机中并实时运行，下位机装有AD 和DA板卡，实现对伺服阀和电磁换向阀控制以及拉压力传感器和位移传感器的信号采集，并形成闭环系统。同时，上位机对系统运行状态进行实时监控。

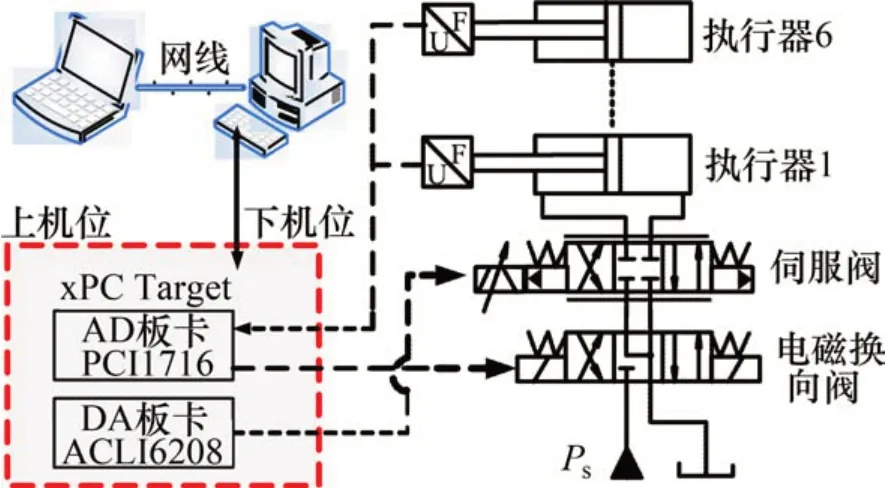
图10 实验方案Fig.10 Experimental scheme

4.2 阶跃响应实验分析

为验证复合控制器降低超调以提高稳定性的有效性，对多维力加载实验台阶跃力响应进行研究，给定关节空间CMAC 神经网络泛化参数c=5，网络学习效率μ=0.1，动量因子α=0.04，PID 参数各作动器单独调节，受非线性因素影响，6条作动器PID参数取值并不相同。给定沿X轴方向初始值为400 N 且稳态值为800 N 的阶跃信号，对比3 种控制器下力响应曲线，如图11所示。

从图11可看出：PID控制器、模糊PID控制器和CMAC-模糊PID 控制器下阶跃力响应超调量分别为6.62%，3.75%和1.25%，响应时间分别为0.19，0.18和0.10 s。模糊PID控制器与PID控制器相比，超调量降低43.4%，响应时间无明显缩短。CMAC-模糊PID 控制器与模糊控制器相比，超调量降低66.7%，响应时间缩短44.4%。通过分析不同控制器下单通道阶跃力响应实验结果，验证了CMAC-模糊PID 控制器在降低超调、提高响应速度、提高系统稳定性方面的有效性。

4.3 动态加载耦合力实验分析

为验证CMAC-模糊PID 控制在降低各通道间耦合力方面的有效性，给定沿Y轴和Z轴方向幅值为600 N，频率为2 Hz的正弦力指令，沿X轴方向0 N 的力指令信号，绕Y轴和Z轴方向幅值为100 N·m；给定频率为2 Hz 的正弦力矩指令，绕X轴方向0 N·m 的力矩指令信号。对比PID 控制器、模糊PID 控制器和CMAC 模糊PID 控制器下Fx和Rx加载通道输出力/力矩响应曲线，Fx响应曲线如图12所示，Rx响应曲线如图13所示。

由图12可知：受其他自由度力加载通道耦合力影响，在PID 控制下Fx加载通道耦合力幅值为240 N，模糊PID 控制下Fx加载通道耦合力幅值为175 N，CMAC-模糊PID 控制下耦合力幅值为120 N。与PID 控制器相比，模糊PID 控制器下耦合力幅值降低了27.1%；与模糊PID 相比，CMAC-模糊PID控制器下耦合力幅值降低了31.4%。

图11 单自由度阶跃力加载响应曲线Fig.11 Responding curves of step force loading with single channel

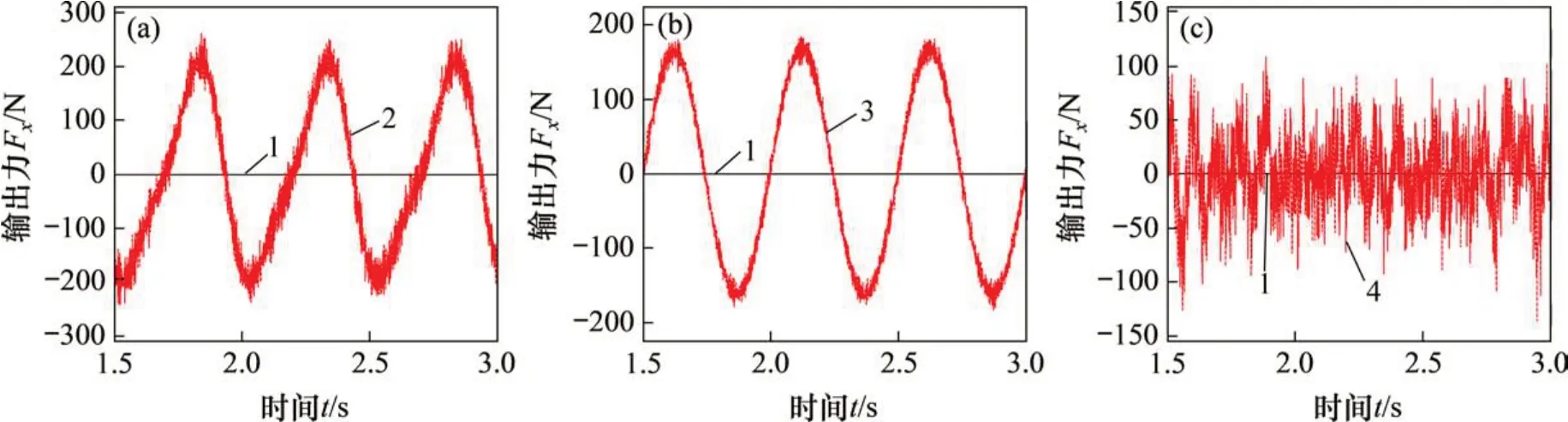
图12 Fx通道响应曲线Fig.12 Responding curves of Fx force loading channel

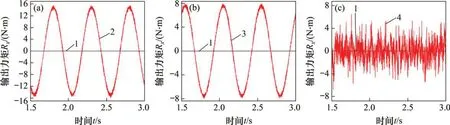
图13 Rx通道响应曲线Fig.13 Responding curves of Rx torque loading channel

由图13可知：在PID 控制下Rx加载通道耦合力矩幅值为15.4 N·m，模糊PID 控制下Rx加载通道耦合力矩幅值为8.0 N·m，CMAC-模糊PID控制下耦合力矩幅值为6.7 N·m。与PID 控制器相比，模糊PID控制器下耦合力矩幅值降低了48.1%；与模糊PID 控制器相比，CMAC-模糊PID 控制器下耦合力矩幅值降低了16.3%。

Fx和Rx加载通道耦合力/力矩在不同控制器下的幅值验证了CMAC-模糊PID 在多维力加载解耦方面的有效性。

4.4 动态力加载实验分析

在多维力加载实验台上进行正弦力/力矩加载，以验证复合控制器提高力加载动态跟踪性能的有效性。同时给定沿X轴、Y轴和Z轴方向幅值均为600 N，频率为2 Hz的正弦力指令，绕X轴、Y轴和Z轴方向幅值均为100 N·m，频率为2 Hz的正弦力矩指令，对比3种控制器下的响应曲线，如图14所示。

图14 六自由度动态力/力矩响应曲线Fig.14 Dynamic force/torque responding curves of 6-DOF force loading channel

从图14可看出：动态力加载时，Fx和Fy加载通道响应性能相似，以Fx加载通道为例，在PID控制下Fx加载通道力响应幅值为547 N，与指令信号相比，力幅值降低了53 N。模糊PID 控制下Fx加载通道力响应幅值为580 N，与指令信号相比，力幅值降低了20 N；Fx加载通道模糊PID 控制与PID 控制相比，力幅值衰减降低了62.3%。在PID控制下，Fz加载通道力响应幅值为384 N，与指令信号相比，力幅值降低了116 N。模糊PID 控制下力响应幅值为521 N，与指令信号相比，力幅值降低了79 N；模糊PID控制与PID控制相比，力幅值衰减降低了31.9%。与指令信号相比，在CMAC-模糊PID控制下，Fx，Fy和Fz加载通道几乎没有力幅值衰减与相位滞后，动态力跟踪效果良好。

Rx，Ry和Rz加载通道响应性能相似。以Rx加载通道为例，在PID控制器下，Rx加载通道力矩响应幅值为93 N·m，与指令信号相比，力矩响应幅值降低了7 N·m。模糊PID控制下Rx加载通道力矩响应幅值为96 N·m，与指令信号相比，力矩响应幅值降低了4 N·m，模糊PID 控制与PID 控制相比力矩幅值衰减降低了42.9%。与指令信号相比，在CMAC-模糊PID 控制下，几乎没有力矩幅值衰减与相位滞后，正弦力矩跟踪效果良好。

通过分析六自由度力/力矩加载在不同控制器下幅值衰减情况可知，在CMAC-模糊PID 控制器下，力/力矩响应几乎没有幅值衰减与相位滞后，力加载动态跟踪性能良好。

5 结论

1)提出了一种CMAC-模糊PID控制策略，有效降低了系统自身结构与参数摄动对液驱并联机构多维力加载系统控制精度的影响。

2)系统广义质量阵为非对角阵，由此产生的惯性力耦合为通道间力/力矩耦合的主要因素。

3)利用模糊控制实时调整PID 控制器参数，降低了干扰对系统稳定性的影响，提高了控制系统的灵活性。与PID控制器相比，在模糊PID控制下，静态力加载超调量降低43.4%，动态力加载通道间耦合力幅值降低27.1%，幅值衰减降低31.9%，系统超调量明显降低，幅值衰减、通道间耦合现象明显减少。

4)将单通道力指令与模糊PID 控制器输出作为CMAC前馈控制的训练样本，随训练样本增加，CMAC 控制精度不断提高。与模糊PID 控制器相比，在CMAC-模糊PID 控制下进行静态力加载时，超调量降低66.7%，响应时间缩短44.4%，动态力加载通道间耦合降低16.3%，与指令信号相比，几乎没有力/力矩幅值衰减与相位滞后，控制精度明显提高。