四维超混沌系统及其在数据加密中的应用

欧国成，刘小园

(罗定职业技术学院信息工程系，罗定 527200)

当今社会信息安全是影响国家安全的一个重要因素，关系到国家金融环境、意识形态、政治氛围等各个方面，是社会稳定的可靠保障，而数据加密技术是保障信息安全的有效措施。现代数据加密技术主要有对称加密和非对称加密2种，在实际应用中，非对称加密主要用于认证和密钥管理等，对称加密主要用于大量数据的加密，其中AES算法是对称加密中最流行的算法之一[1]。

混沌(Chaos)是一种在确定性动力学系统中表现出的不可预测、类似随机的运动形式。混沌具有遍历性、不可预测性、类随机性、对初值极端敏感性等特性，使其在密码学和信息安全领域得到了极大的重视。与混沌系统相比，超混沌(Hyperchaotic)系统具有2个或2个以上的正李雅普诺夫(Lyapunov)指数，具有更复杂的动力学特性，在信息安全领域中具有更高的实用价值[2]。

近年来，学者们针对混沌数据加密提出了许多方案。林振荣等[3]提出一种基于超混沌序列和位平面置乱的图像加密方法，增大了密钥空间，提高了图像加密的安全性；Khadijeh等[4]提出一种超混沌图像加密算法，算法鲁棒性好但加密速度不够理想；刘海峰等[5]设计了一种基于超混沌与圆锥曲线的混合加密算法，提高了算法安全性，但混合加密算法要比单个加密算法的执行效率低；温贺平等[6]提出一种基于Hadoop的超混沌加密算法，结合Hadoop平台的MapReduce并行编程模型，设计兼具较高执行效率和安全性的密码算法，但算法运行环境受到了限制；韩雪娟等[7]将图像分块置乱和整体行列置乱相结合，在扩散的过程中通过改进的超混沌产生更具有伪随机性的密钥流进行多次加密，解决了密文容易破解的问题；杨丹等[8]提出一种基于超混沌和分块操作的快速图像加密算法，通过建立密钥和明文的关联，提高密钥敏感性；王丽娟等[9]提出了一种基于动态参数控制的混沌系统图像加密算法方案，解决了混沌系统随机性不高、结构简单、具有周期性等问题。

现有的混沌加密方案大多用于图像加密或者运行于分布式平台，应用于文本数据加密的方案极少。针对以上问题，本文利用超混沌系统复杂的动力学特性，设计一种密钥空间大、密钥敏感性好、加解密效率高的超混沌数据加密算法，用于保障数据安全。

1 四维超混沌系统

现有的超混沌系统大多数是在三维混沌系统的基础上通过增加一个自变量，并增加一个微分方程构造而成[10]。张莉等[11]构造了一个具有四翼超混沌吸引子的非线性系统，通过对Poincaré截面、吸引子和Lyapunov指数等分析揭示新系统中超混沌吸引子的存在；扶坤荣[12]基于三维增广Lü系统，构建了一个四维耗散超混沌系统，其数学模型为：

(1)

式中：x、y、z、w为系统的4个状态变量；a、b、c、d为系统的控制参数。

2 超混沌系统特性分析

当系统(1)的控制参数[a，b，c，d]=[6，4，8，2]时，系统处于超混沌状态，分别对系统的Lyapunov指数、Lyapunov维数、超混沌吸引子相图、时间响应图、初值敏感性等特性进行分析。

2.1 Lyapunov指数

Lyapunov指数用于表示相空间相邻轨迹的平均指数发散率，正的Lyapunov指数是判断系统是否处于混沌状态的必要条件。非线性系统只要有1个大于零的Lyapunov指数，就会出现混沌现象。若系统具有1个以上正的Lyapunov指数，则称为超混沌系统。

当系统(1)的控制参数[a，b，c，d]=[6，4，8，2]，4个状态变量的初始值[x0，y0，z0，w0]=[1，2，3，4]时，计算出4个Lyapunov指数分别为：LE1=1.788，LE2=0.113，LE3=0，LE4=-37.773，此时，系统(1)处于超混沌状态。Lyapunov维数(DL)反映了混沌吸引子结构的复杂性和几何特征，按式(2)计算，可得DL=3.05。

(2)

2.2 超混沌吸引子

采用龙格-库塔法对式(1)进行微分方程求解，并利用MATLAB软件进行数值仿真，当控制参数[a，b，c，d]=[6，4，8，2]，变量初值[x0，y0，z0，w0]=[1，2，3，4]时，系统存在超混沌吸引子，如图1所示。

状态变量x、y的时间响应图如图2所示，可见变量在时域上是连续的、具有不可预测性和非周期性等特点，适合用于数据加密。

2.3 初值敏感性

保持系统(1)的控制参数[a，b，c，d]=[6，4，8，2]不变，把状态变量x的初始值x0由1变为1.000 001，其余变量的初始值保持不变，得到x的时域波形如图3所示。

尽管状态变量x的初始值改变了0.000 1%，但x很快就发生了巨大的偏差，可见系统(1)对初始条件具有极端敏感性。初值敏感性是混沌系统的最大特点，在数据加密中，把系统的初始值作为加密密钥，使混沌加密具有良好的保密性。

3 超混沌分组数据加密

当系统(1)处于超混沌状态时，所产生的混沌序列具有不可预测性、非周期性、对初始条件极端敏感性，适合用于数据加密。下面介绍一种超混沌分组数据加密方案，如图4所示，具体步骤如下：

1) 选取密钥参数。保持系统(1)的控制参数不变，使系统处于超混沌状态，以系统4个状态变量的初始值[x0，y0，z0，w0]为密钥。

2) 产生超混沌序列。采用四阶龙格-库塔法对超混沌系统进行离散化处理，将迭代步长设置为0.002，为增加随机性，舍去前面1 000次迭代的值，得到4个超混沌序列Kx、Ky、Kz、Kw。

3) 生成加密密钥。在分组数据加密中，数据分组长度由分组模式决定，每组数据需要进行2次加密，加密密钥长度和数据分组长度一致。通过把Kx、Ky、Kz、Kw分别进行小数点移位、取模、取整运算得到4个取值范围为[0，255]的伪随机序列，处理方法如下：

(3)

在式(3)中，round为四舍五入取整函数，mod为取模函数，floor为向下取整函数，经过上述处理后得到的混沌序列，取值范围为[0，255]，适合用于字节加密运算。

为了打乱4个状态变量之间的关联性，进一步提高密钥的安全性，把Kx、Ky、Kz、Kw进行异或运算，得到加密密钥key1、key2，具体操作如下：

(4)

式中:⊕表示按位异或运算；所得的key1、key2分别为2轮加密的密钥。

4) 明文数据分组加密。先把明文数据M按照分组模式进行数据分组，每组数据依次进行2轮加密操作，最后得到密文C。数据分组长度以及密钥长度由分组模式决定，在本方案中，分组模式有4种，分别为64字节、128字节、256字节、512字节。数据加密效率与分组模式有关，下文会进行详细对比。

5) 解密过程。超混沌分组数据加密方案是一种对称加密算法，解密是加密的逆过程。当解密密钥和加密密钥一致时，密文C经过解密1、解密2两轮解密，可得到原始明文M。由于超混沌系统对初始条件具有极端敏感性，解密过程的密钥参数必须和加密过程的密钥参数一致，才能得到相同的密钥，否则无法正确解密出原始明文。

4 实验结果分析

按照本文提出的超混沌分组数据加密方案，基于MATLAB图形用户界面(GUI)功能开发了超混沌数据加密系统，如图5所示。用户可以通过设置四维超混沌系统初始值来产生超混沌序列，进而生成加密密钥；可以对分组数据长度进行设置，有4种模式可以选择；可以手动输入明文数据，也可以通过文件形式导入待加密的数据；通过点击“Encrypt”按钮对明文进行加密，点击“Decrypt”按钮对密文进行解密，点击“保存密文”按钮把密文保存为文件输出。系统能够直观地显示加密前的明文和加密后的密文，显示加密所用时间和解密所用时间。

4.1 密钥空间分析

本算法以超混沌系统的4个状态变量的初始值{x0，y0，z0，w0}为密钥，x0、y0、z0、w0均为双精度类型，精度为10-15，可计算出本算法的密钥空间为1015×4=1060≈2199，即密钥长度为199 bit。本算法的密钥长度与其他经典对称加密算法的密钥长度对比情况如表1所示。

表1 几种对称加密算法密钥空间对比Tab.1 Comparison of key spaces of several symmetric encryption algorithms

从表1可以看出，本算法的密钥长度优于其他几种经典对称加密算法，仅次于AES-256算法。若把超混沌系统的4个控制参数a、b、c、d也作为密钥参数，算法的密钥长度可进一步变长，密钥空间可进一步扩大。

要想对此算法进行暴力破解，假设每秒钟尝试10亿亿次不同的组合(我国的神威·太湖之光超级计算机的峰值性能为12.5亿亿次/s，持续性能为9.3亿亿次/s)，暴力破解需要用1060/(10×108×108×86400×365)≈3.17×1035年(太阳寿命约为4.57×109年)，可见本算法具有足够大的密钥空间，足以抵抗现有运算速度的暴力破解攻击。

4.2 密钥敏感性分析

首先把密钥参数设置为x0=1、y0=1、z0=1、w0=1，对明文数据M执行加密操作，得到相应的密文数据C，然后把密钥参数x0修改为1.000 000 001，其他3个密钥参数保持不变，对密文数据C执行解密操作，结果由于解密密钥与加密密钥不一致，导致解密失败，如图6所示。

可见，本算法具有良好的密钥敏感性，尽管密钥参数变化很小，却无法通过解密得到正确的明文数据。

4.3 加解密效率分析

本算法具有4种分组数据长度可以选择，分别是64字节、128字节、256字节、512字节，分组数据长度会影响数据加解密的速度。下面以100、200、400 kB 3组明文数据为例，分别计算不同分组长度的加密时间，对比情况如图7所示。可见，分组数据长度越大，加密效率越高。

以100 kB明文数据为例，将本算法与高级加密标准(AES)算法的加解密效率进行对比。AES是对称密钥加密中最流行的算法之一，有3种不同的加密模式，分别为AES-128、AES-192、AES-256，为方便阐述，把本算法的4种分组模式分别记为HEA-64、HEA-128、HEA-256、HEA-512。为保证实验数据的公平性，在同一台计算机上分别利用AES算法和本文算法对同一份明文数据样本进行加密、解密操作，分别记录所需的加密时间和解密时间，如表2所示。

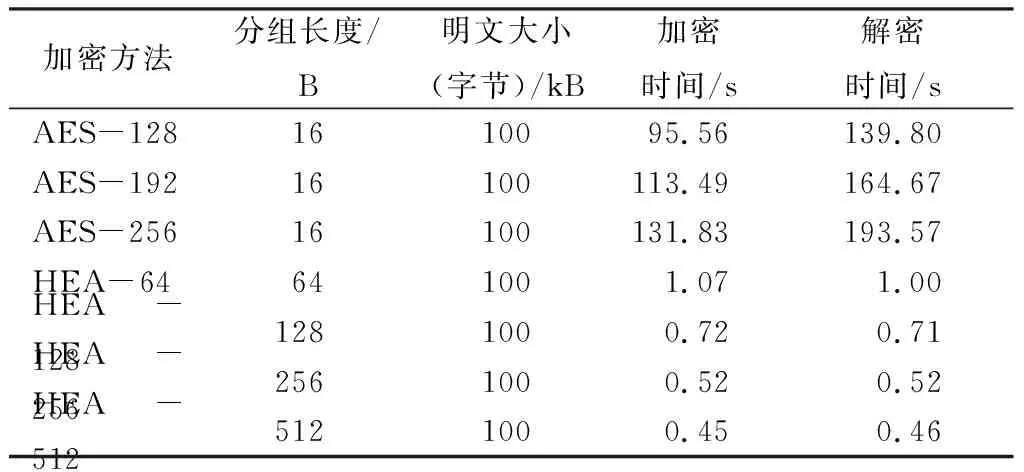
表2 加解密效率对比Tab.2 Comparison of encryption and decryption efficiency

从表2可见，本算法的加解密效率远远高于AES算法的加解密效率。其中原因有2个:一是本算法的数据分组长度比AES算法所固定的16字节长；二是本算法的加密过程只需要进行2轮加密，而AES-128需要进行10轮迭代加密、AES-192需要进行12轮迭代加密、AES-256需要进行14轮迭代加密。

5 结论

通过对四维超混沌系统的复杂动力学特性进行研究，利用超混沌系统的不可预测性、非周期性、对初始条件的极端敏感性等特点，设计了一种超混沌分组数据加密方法。实验表明，该算法具有足够大的密钥空间，可抵御暴力破解攻击，具有良好的密钥敏感性、加解密效率高等特点，适合用于大量数据的加密。