基于FGM函数的不同贮备部件下两部件串联系统的优劣分析

梁叶子

(陆军步兵学院演训中心，江西 南昌330103)

在实际的系统工程中，一些设备对于系统的可靠性要求较高，为了提高系统的可靠度，往往会通过对失效率较高的部件添加贮备部件的方式来提升整体系统的可靠度。对系统的可靠度进行分析时，往往假设系统部件互相独立[1-4]。在实际的系统工程中，系统是一个整体，系统中的每个部件之间相互影响，彼此相依，copula函数[5-10]可用于分析相依系统的可靠性，其中FGM copula函数具有很好的性质，用途较广。孙永波[11]研究了基于FGM copula不同类型的关联系统的可靠性，梁叶子[12]研究了基于FGM copula函数下带1个贮备部件的两部件串联系统如何进行优化。本文基于FGM copula函数对不同贮备类型下的两部件串联系统的可靠度进行分析，提出了用可靠度/成本作为衡量系统优劣指标，系统分析了不同贮备类型下的两部件串联系统的优劣。

1 FGM copula函数模型

Sklar定理[13]对于随机变量X=(X1,X2，…，Xn)，假设F是n维联合分布函数，对应的边缘累计分布函数为FX1，FX2，…，FXn，则存在copula函数C，对∀x=(x1,x2，…，xn)∈Rn，有如下等式成立：

F(x1，x2，…，xn)=C(FX1(t),FX2(t)，…，FXn(t))

对于FGM copula函数，若边缘分布函数FXi,(i=1,2，…，n)连续，则copula函数唯一。

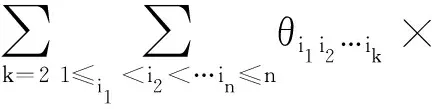
此时每个copula是绝对连续的，c(u)为copula函数的联合概率密度函数：

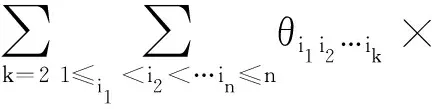
其中FGM二维copula函数族：

C(u,v)=uv+θuv(1-u)(1-v),θ∈[-1,1]

其密度函数为：

c(u,v)=1+θ(1-2u)(1-2v)

FGM三维copula函数族：

C(u,v,w)=uvw[1+θ1(1-u)(1-v)+
θ2(1-u)(1-w)+θ3(1-v)(1-w)+
θ4(1-u)(1-v)(1-w)]

2 带1个冷贮备的两部件串联系统可靠性

系统由部件1，1′，2三部件组成，其中1′是1的冷贮备部件，部件1、2串联，系统可靠性框图如图1所示。

模型假设：

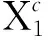
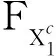
3) 系统的转换开关完全可靠。

4) 系统在t=0 时刻是完美的。则部件 FGM copula相依下带1个冷贮备的系统寿命：

用RC(t)部件FGM copula相依下带1个冷贮备的系统可靠度：

其中

求得部件相依系统可靠度：

RC(t)=1-[1+(3θ1-λ1θ1t-λ1t-1)e-λ1t-
(2θ1λ1t+3θ1)e-2λ1t]-[1-e-λ2t]+[1-e-λ2t]×
[1+(3θ1-λ1θ1t-λ1t-1)e-λ1t-(2θ1λ1t+
3θ1)e-2λ1t]+θ1[1-e-λ2t][1+(3θ1-λ1θ1t-
λ1t-1)e-λ1t-(2θ1λ1t+3θ1)e-2λ1t][(2θ1λ1t+
3θ1)e-2λ1t-(3θ1-λ1θ1t-λ1t-1)e-λ1t]e-λ2t

3 带1个温贮备的两部件串联系统可靠性

系统由部件1、2、1′三部件组成，其中部件1′是部件1的温贮备部件，部件1、2串联，系统可靠性框图如图2所示。

模型假设：

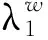
3) 其余假设同第2小节中的模型假设。

则部件FGM copula相依下带1个温贮备的系统寿命：

用RW(t)部件FGM copula相依下带1个冷贮备的系统可靠度：令

则：

其中

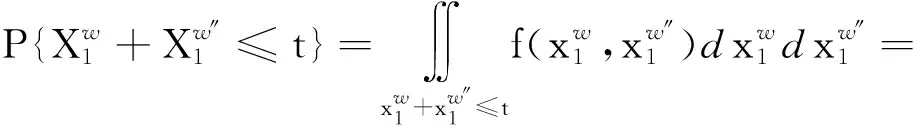
求得部件FGM copula相依下带1个温贮备的系统可靠度：

4 带1个热贮备的两部件串联系统可靠性

系统由部件1，2，1′三部件组成，其中1′是1的热贮备部件，1,2串联，系统可靠性框图如图3所示。

模型假设：

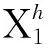
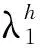
3) 其余假设同第2小节中的模型假设。

则部件FGM copula相依下带1个热贮备的系统寿命：

用RH(t)表示带1个热贮备部件的系统可靠度。

则：

其中：

C(FX1(t),FY1(t),FX2(t))=
FX1(t)FY1(t)FX2(t)[1+θ1(1-FX1(t))(1-
FY1(t))+θ2(1-FX1(t))×
(1-FX2(t))+θ3(1-FY1(t))(1-FX2(t))+
θ4(1-FX1(t))(1-FX2(t))(1-FX2(t))]=
(1-e-λ1t)2e-λ2t[1+θ1e-2λ1t+θ2e-λ1te-λ2t+
θ3e-λ1te-λ2t+θ4e-2λ1te-λ2t]

求得系统可靠度：

RH(t)=1-(1-e-λ2t)-(1-e-λ1t)2(1+
θ1e-2λ1t)+(1-e-λ1t)2e-λ2t[1+θ1e-2λ1t+
θ2e-λ1te-λ2t+θ3e-λ1te-λ2t+θ4e-2λ1te-λ2t]

5 不同贮备部件下的两部件串联系统优劣分析

可靠性固然是评判一个系统好坏的一个很重要的指标，但是在实际应用中系统的好坏受到很多因素的影响，根据经验其中可靠性和成本是我们评判一个系统优劣的最重要的两个指标。在这里用可靠度/成本即单位成本下的可靠度，作为评判系统优劣的指标。

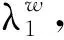
带有1个冷贮备两部件串联系统的成本表示为PC，带有1个温贮备两部件串联系统的成本表示为PW，带有1个热贮备两部件串联系统的成本表示为PH,则有：

PH=P1+P1+P2

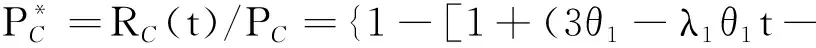
上述式子分别是带1个冷贮备的两部件串联系统的单位成本下的可靠度、带1个温贮备的两部件串联系统的单位成本下的可靠度以及带1个热贮备的两部件串联系统的单位成本下的可靠度，在实际的系统运用中，可根据实际情况带入相应的式子来评判系统的优劣。

6 数值算例

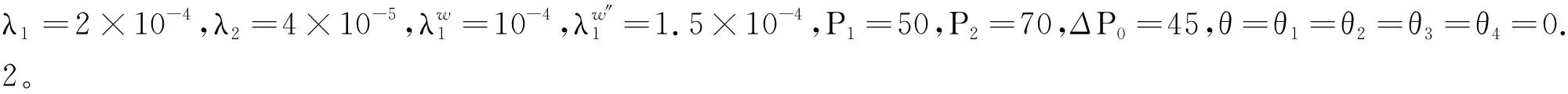
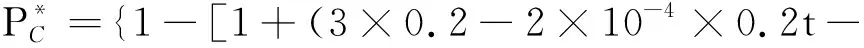
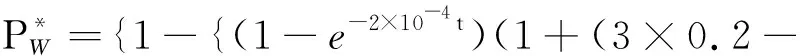
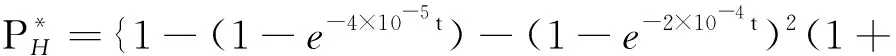
单位成本下的可靠度随时间变化曲线如图4所示。

可以得出，在一组特定参数下，假设两部件串联系统的使用寿命为10 000 h，那么对这个系统增加温贮备或者热贮备比增加冷贮备的性价比更高。如果对这个系统的使用寿命要求不高，在7 595 h之前，那么可以选择对该系统增加温贮备。如果系统的使用寿命要求比较高，选择对该系统增加热贮备性价比更高。

7 结论

本文分析了3种不同贮备类型下的两部件串联系统的优劣。推导出了不同贮备类型下两部件串联FGM相依系统的可靠度以及对应系统的性价比。结合实例，分析并求出不同寿命要求下的性价比更高的贮备系统。研究结果为现实串联系统如何选择贮备部件提供了理论参考。但是对于一些构造复杂的串并联系统如何添加贮备部件才能使得系统的性价比更高，有待进一步的研究。