支承体系对多塔矮塔斜拉桥横向地震响应的影响

邓治国 王 琦 李建中，*

（1.山西路桥桥隧工程有限公司，朔州036005；2.同济大学土木工程学院桥梁工程系，上海200092）

1 概 论

矮塔斜拉桥是介于斜拉桥和连续梁之间的一种组合体系桥型［1］，因其具有竞争力的结构特性和优美造型，在国内越来越受到重视［2］。其中，多塔矮塔斜拉桥发展迅速，如已建成的宁江松花江特大桥、南昌朝阳大桥以及正在建设的运宝黄河大桥均为多塔矮塔斜拉桥。由于多塔矮塔斜拉桥结构的质量和刚度都相对较大，地震作用下产生的反应也较大，其抗震性能引起许多学者的关注。上官萍等［3］以典型的两塔矮塔斜拉桥为背景，分析了塔墩支撑变化、主梁高跨比、边主跨比、主塔的刚度和高度等参数对于矮塔斜拉桥地震响应的影响。陈维等［4］以宁江松花江特大桥为背景，研究了多塔矮塔斜拉桥纵桥向结构体系对地震响应的影响。龚志勇［5］对一座三塔四跨双索面矮塔斜拉桥做了理论计算分析，分析行波效应对其地震反应的影响，并使用液体黏滞阻尼器对该桥做了减震设计。但这些研究主要是针对纵桥向进行的，目前对多塔矮塔支承体系横桥向地震反应以及横向减震的研究相对较少。

本文以运宝黄河大桥为背景，针对多塔矮塔斜拉桥结构特点，分别比较了塔梁固接、塔墩分离，塔墩固接、塔梁分离，塔、墩、梁固接三种不同支承体系横桥向地震反应特点，并研究了同一规格摩擦摆支座对不同体系多塔矮塔斜拉桥的横向减震效果。

2 背景工程与有限元模型

2.1 背景工程

运宝黄河大桥主桥为采用110 m+2×200 m+110 m 布置的波形钢腹板多塔矮塔斜拉桥。全桥共有五个墩，分别编号为G1、T1、T2、T3、G2，如图1 所示。下部结构构造T1～T3 主墩采用双薄壁实体墩，基础采用灌注桩基础。其中T1、T2、T3塔的连接采用塔、梁、墩固结的方式，主塔的桥塔尺寸（图2）和承台尺寸（34.6 m×24.2 m×5 m）相同，T1塔由于地址条件不同，使得设计上其与T2 和T3的墩高不同，T1 墩的墩高为39.6 m，T2 与T3 墩的墩高为45.6 m，主塔桥墩侧面与立面示意图见图3，桥塔与桥墩截面三塔均相同，过渡墩上的墩梁连接方式则为纵横桥向放开。

主梁横断面采用单箱五室单幅断面，除中室腹板采用混凝土腹板外，边腹板、次边腹板共4道全部采用波形钢腹板。箱梁顶面宽34 m，底宽25 m，翼缘宽度为4.5 m，跨中主梁横断面如图4所示。

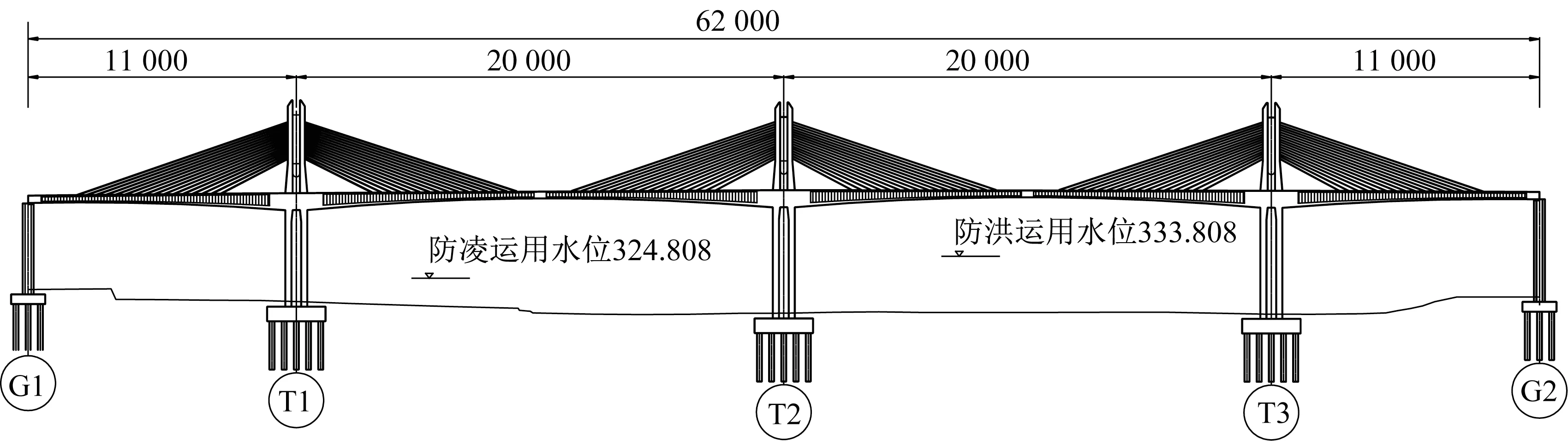
图1 运宝黄河大桥主桥桥型布置图（单位：cm）Fig.1 Yun Bao yellow river bridge main bridge type layout diagram（Unit：cm）

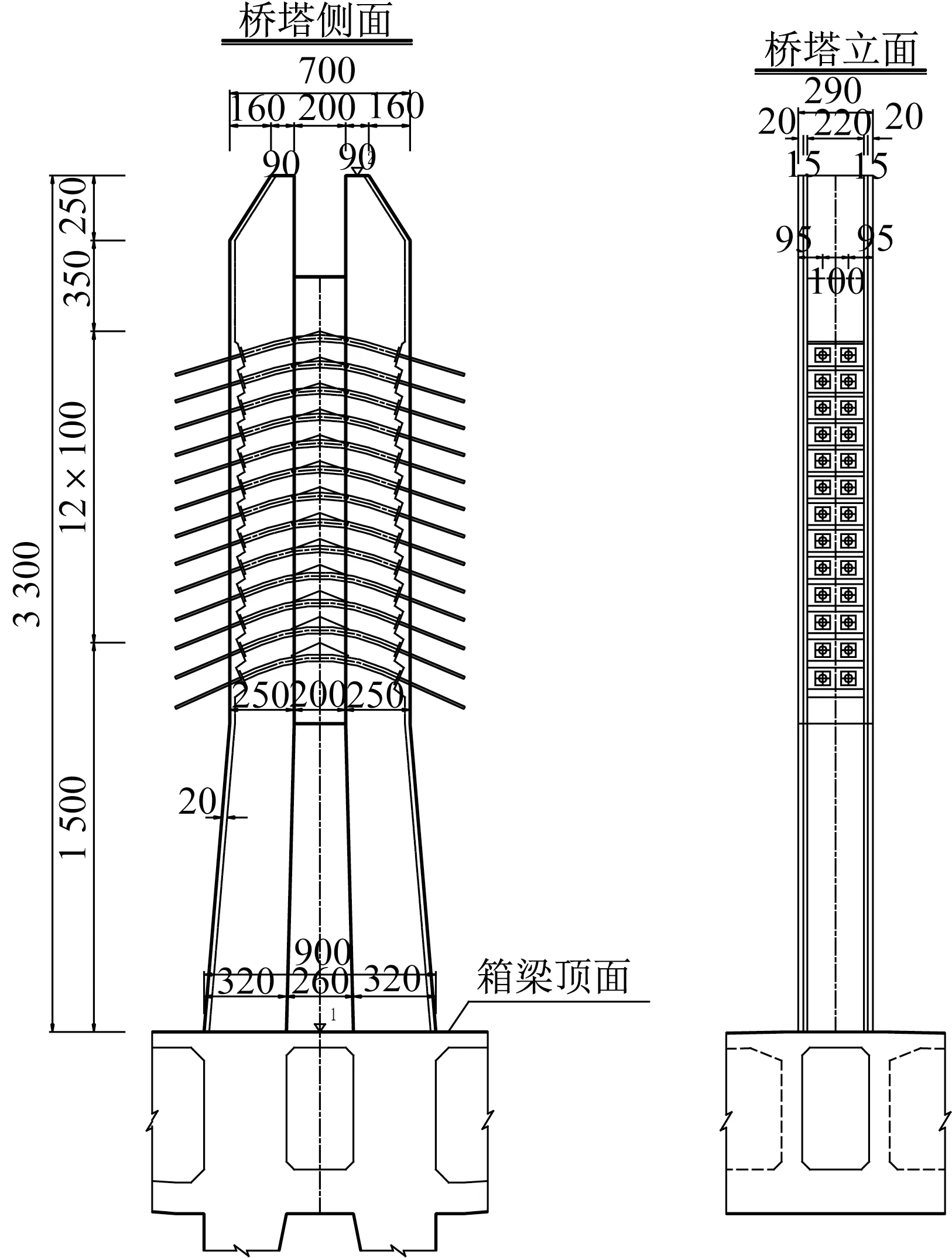
图2 运宝桥桥塔构造（单位：cm）Fig.2 Bridge tower structure of Yun Bao Bridge（Unit：cm）

图3 运宝桥墩柱构造图（单位：cm）Fig.3 Pier structure of Yun Bao Bridge（Unit：cm）

图4 运宝桥跨中主梁截面（单位：cm）Fig.4 Cross-middle main beam cross section of Yun Bao Bridge（Unit：cm）

2.2 有限元模型与比较体系

以运宝河黄河大桥为背景，采用大型有限元计算软件SAP2000 分别建立了塔梁固接、塔墩分离，塔墩固接、塔梁分离，塔、墩、梁固接三种不同支承体系的空间有限元模型，如图5所示。

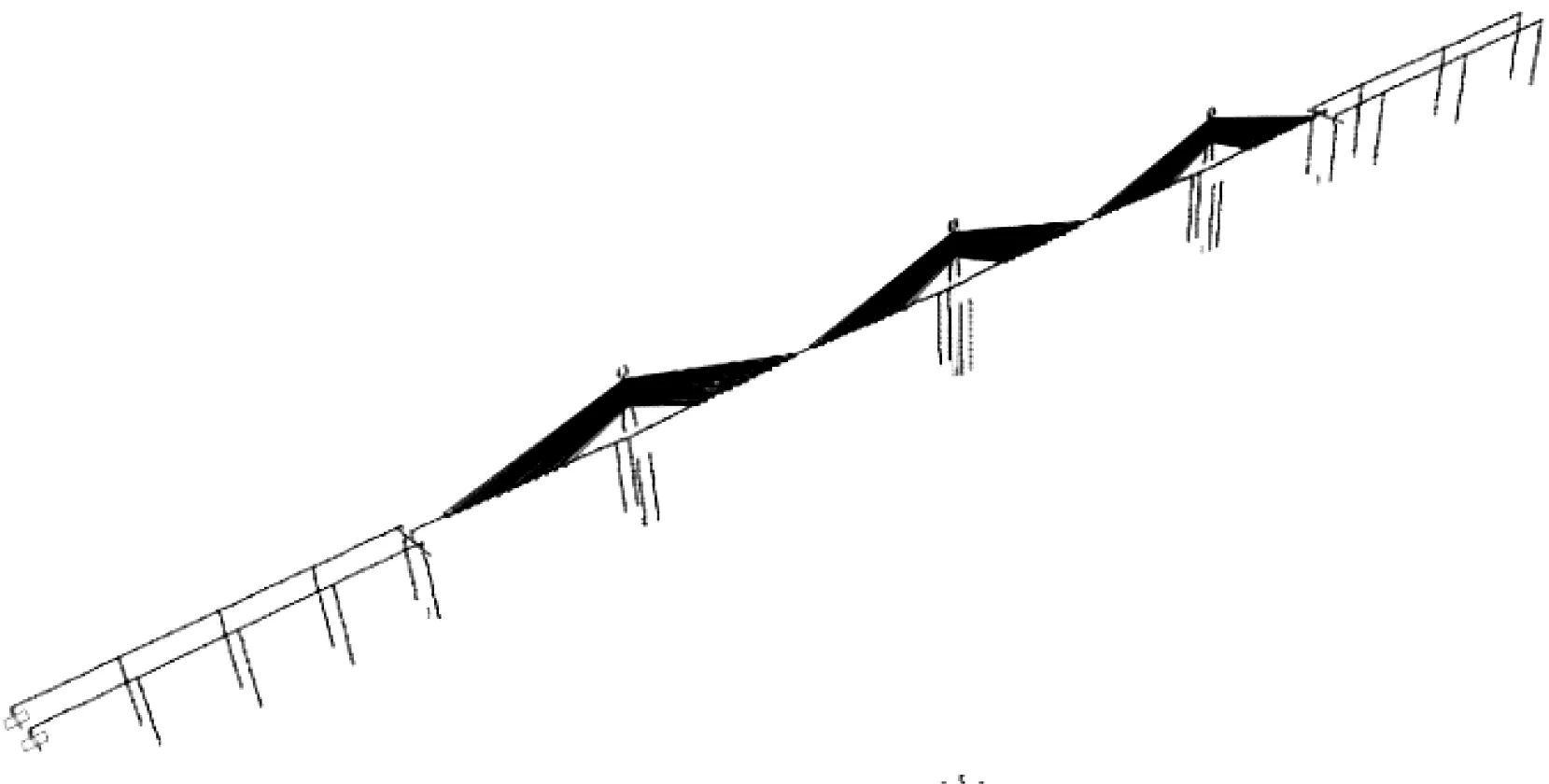
图5 结构有限元模型Fig.5 Structural Finite element model

在建立空间有限元模型时，主梁、主塔、边墩均采用空间梁单元模拟。主梁采用单梁式模型，斜拉索采用空间桁架单元模拟，以Ernst公式修正拉索弹性模量，拉索与主梁及主塔均采用主从连接，同时考虑了主塔、主梁、拉索及边墩由于恒载作用而引起的轴力对几何刚度的影响。在横向固定工况中，桥墩与塔（梁）分离时，以支座变形不影响结构位移变化为准则采用大刚度支座进行连接。桩基础以承台底六弹簧模拟。引桥对主桥的影响效应采用在主桥两侧各加一联引桥模型模拟。

本文比较的三种体系中，以塔、墩、梁固结体系为原桥体系即基准体系，塔梁固结、塔墩分离体系为比较体系A（简称为体系A），塔墩固结、墩梁分离体系为比较体系B（简称为体系B）。

2.3 地震动输入

本文以该桥所在场地50年超越概率为2%水平下自由场一般冲刷线处的加速度反应谱为目标谱拟合了7 条水平时程波，相应的竖向地震作用为水平地震作用的0.65 倍，时程分析结果取7 条波最大值的平均值。人工波及转化反应谱与目标谱的比较见图6与图7。

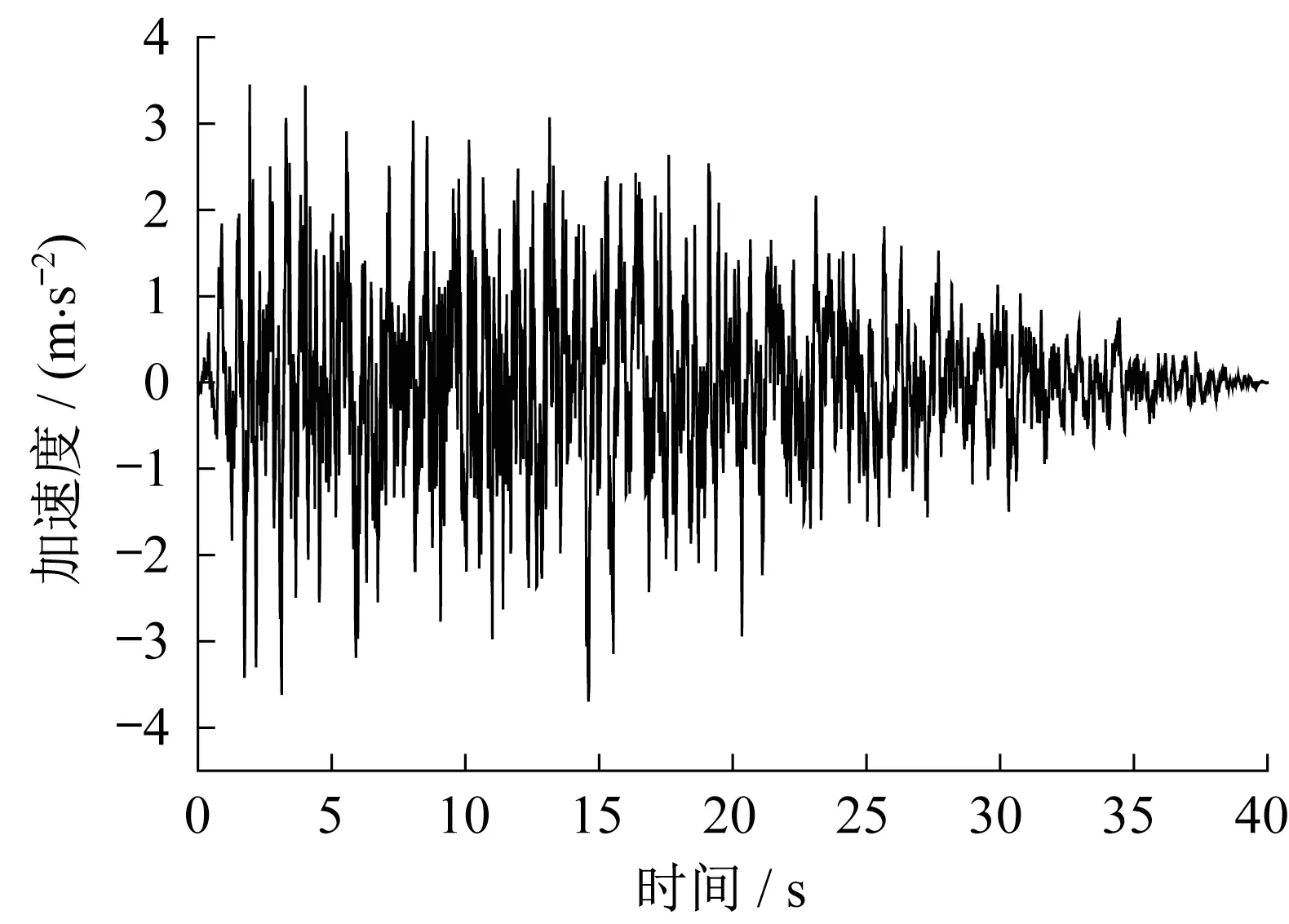
图6 E2概率下典型加速度时程Fig.6 Typical acceleration time path under E2 probability

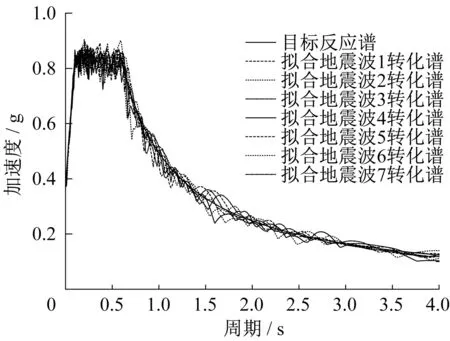
图7 拟合地震波转化谱与规范反应谱Fig.7 Artificial fitting seismic wave reaction spectrum compared to that from the seismic code

3 支承体系对横向地震响应的影响

3.1 支承体系对横向动力特性的影响

表1 给出了不同支体系结构前五阶横向振型的自振频率和振型特点。由于3 种体系梁与塔（墩）之间在横桥向均采用固定连接，由表1 可以看出不同体系多塔斜拉桥的振动周期与振型接近，多塔矮塔斜拉桥的横向振型主要表现为各塔墩一致的横向侧弯以及桥塔的横向振动。

3.2 支承体系对横向地震响应的影响

输入拟合生成的七条场地人工波，按《公路桥梁抗震设计细则》［6］的要求，取7 条地震波计算结果的平均值，得到的不同支承体系墩底弯矩变化、塔底弯矩、塔顶位移与结构支座剪力结果，如图8所示。

表1 不同体系结构动力特性Table 1 Dynamic characteristics of defferent support system

图8 可以看出，三种支承体系的墩底弯矩变化、塔底弯矩、塔顶位移相差不大，最大相差在10%以内，这主要是因为三种体系梁体与塔之间的横向连接都是采用固接，与三种体系横向动力特性相同的结论一致。但横桥向地震作用下，塔梁固结、塔墩分离和塔墩固结、墩梁分离体系的支座剪力差距较大。塔梁固结、塔墩分离体系下，最大支座剪力达894 244 kN，而塔墩固结、塔梁分离体系下最大支座剪力仅为593 172 kN，塔梁固结、塔墩分离体系剪力是塔墩固结、墩梁分析体系剪力的1.5倍。这是由于支撑体系不同造成的，塔梁固结、塔墩分离体系，桥塔和主梁的横向地震力通过支座传递给桥墩，而塔墩固结、墩梁分离体系仅有主梁的横向地震力是通过支座传递给桥墩，因此造成塔梁固结、塔墩分离体系的支座剪力较塔墩固结、塔梁分离体系的支座剪力要大。

图8 三种体系的地震响应比较Fig.8 Comparison of seismic response of three support systems

4 横桥向减震体系

图9 双曲面球型减隔震支座的构造示意Fig.9 Configuration of the double spherical bearing

由以上研究可以看出，由于以上三种结构支承体系在梁体与塔（墩）间采用固定约束，地震输入下，多塔矮塔斜拉桥的横向反应较大，为了减小多塔矮塔斜拉桥的横向地震响应，本文提出采用双曲面减隔震支座，以减小多塔矮塔斜拉桥的横向地震响应。双曲面球型减隔震支座是通过对技术上非常成熟的球形滑动支座进行改造而开发的［7］。该支座将普通球形滑动支座的平滑动面改为球面，结构上包括一个具有滑动凹球面的上支座板、一个具有双凸球面的中支座板和一个具有转动凹球面的下支座板（图9）。滑动面和转动面都是由不锈钢板和聚四氟乙烯板组成的。

在正常情况下（非地震时），支座的固定方向均受限位装置的约束，仅满足梁体转动要求；滑动方向可满足梁体位移要求。在超过装置的承载能力后，限位装置剪断，固定方向也滑动，起到减隔震作用。

双曲面球形球钢支座的力-位移曲线用图7双线性模型模拟。图10 中，Fy为临界摩擦力，x 为上部结构与墩顶的相对位移，Xy为临界滑动位移，K1为屈前刚度，K2为屈后刚度。临界滑动摩擦力为

式中：f 为滑动摩擦系数；N 为支座所承担的上部结构恒载反力。

在双曲面球形支座中，临界位移Xy很小（本文取为2 mm）。

对于屈后刚度K2计算公式如下：

式中：R 为双曲面球形支座半径值；N 为支座承担的上部结构恒载反力。

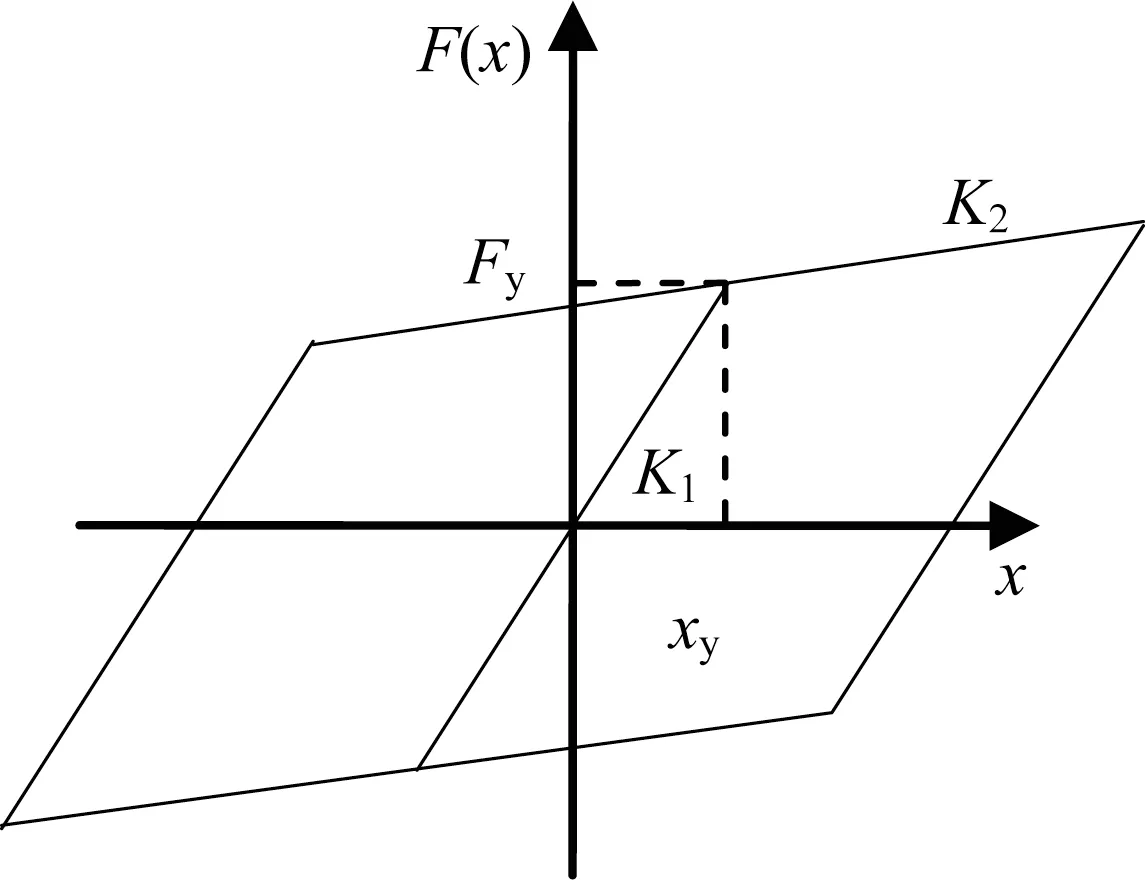
图10 双曲面球形支座恢复力模型Fig.10 Recovery Force model of the double spherical bearing

汤虎对双曲面支座进行了参数分析［8］，发现：①相同摩擦系数条件下，球面半径越小，支座的屈后刚度越大，能提供的摩擦阻力越强，减震效果较好；②相同曲面半径，摩擦系数f 越大，支座屈服强度越大，减震效果越好。本文以摩擦系数为0.03 以及球面半径5 m 为例，比较同一规格的双曲面支座对不同体系的减震效果。

在塔梁固接、塔墩分离体系，塔墩固接、塔梁分离体系中均采用相同的双曲面球形钢支座，以研究不同体系下双曲面减隔震支座的减震效果。表2 为对应于体系A 和体系B 两种体系的双曲面球形球钢支座参数和支座参数的计算。

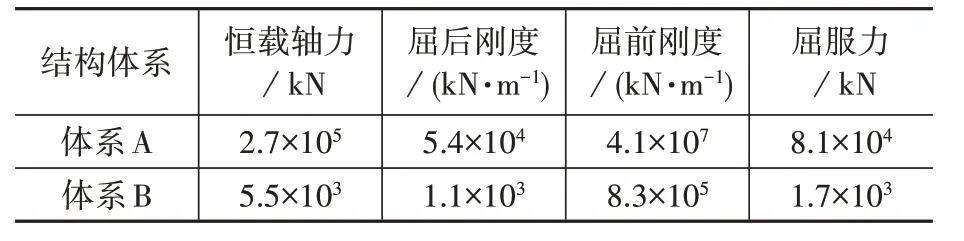
表2 双曲面支座参计算结果Table 2 Calculation results of the double spherical bearing

采用双曲面球型减隔震支座后，得到的多塔矮塔斜拉桥的各塔墩底弯矩变化如表3 和表4 所示，表中同时列出两种体系相对梁、塔（墩）固接的减震率。

表3 体系A受力减震效果Table 3 Force damping effect of support system A

表4 体系B受力减震效果Table 4 Force damping effect of support system B

由表3和表4可以看出，采用双曲面减隔震支座后，两种体系多塔矮塔斜拉桥墩底弯矩和均有减少，但减少程度不同。采用双曲面减隔震支座后，塔墩固结、塔梁分离体系的墩底弯矩减小在80%左右，但塔梁固结、塔墩分离体系的墩底弯矩减少范围在4%～21%。这主要是由于不同支承体系支座承受的反力不同，从而导致双曲面支座滑动摩擦力（表2 中的屈服力）不同。由表2 可以看出，塔梁固结、塔墩分离体系的双曲面支座摩擦力为81 181.8 kN，而塔墩固结、塔梁分离体系双曲面支座的摩擦力仅为1 660.1 kN，远远小于塔梁固结、塔墩分离体系的双曲面支座摩擦力所致。

多塔矮塔斜拉桥采用双曲面球型刚支座后的塔顶位移变化如表5和表6所示。

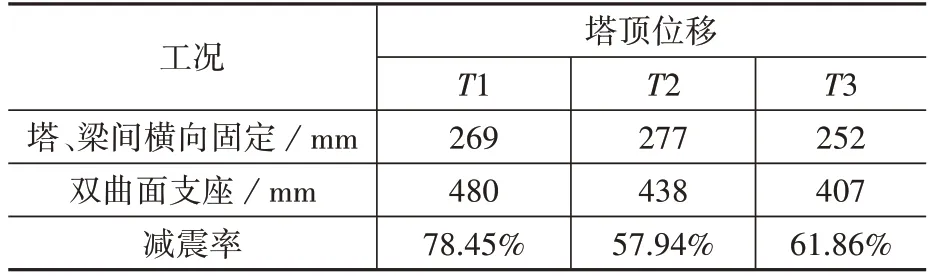
表5 体系A位移减震效果Table5 Dispacement damping effect of support systemA

表6 体系B位移减震效果Table 6 Dispacement damping effect of support system B

由表5和表6可以看出，采用双曲面减隔震支座后，塔梁固结，塔墩分离体系塔顶位移增加较多；但塔梁固结，塔梁分离体系的塔顶位移减小40%左右。

综合比较上述反应可知，双曲面减隔震支座能够有效地减小塔墩固结、塔梁分离体系的地震作用内力，但会显著地增加主梁的位移，因此在主梁与桥塔距离足够的情况下，双曲面减隔震支座对塔墩固结、塔梁分离体系的减震效果要好于塔梁固结、塔墩分离体系。

图11 为7 条地震波输入下，采用双曲面减隔震支座后，2 种体系双曲面减隔震支座的位移比较。从图中可以看出：塔梁固结、塔墩分离体系的支座位移要比塔墩固结、塔梁分离体系的支座位移小得多。因为塔梁固结、塔墩分离体系支座所受到的竖向恒载反力要远远大于塔墩固结、塔梁分离体系支座所受的竖向恒载反力，从而导致地震作用下，塔梁固结、塔墩分离体系的双曲面支座摩擦力远远大于塔墩固结、塔梁分离体系支座摩擦力所致。

图11 双曲面球形支座恢复力模型Fig.11 Recovery Force model of the double spherical bearing

5 结 论

本文针对多塔矮塔斜拉桥结构特点，分别比较了塔梁固接、塔墩分离，塔墩固接、塔梁分离，塔、墩、梁固接三种不同支承体系横桥向地震反应特点，并研究了采用摩擦摆支座减小多塔矮塔斜拉桥横向地震反应的效果。主要结论有：

（1）不同结构体系对多塔矮塔斜拉桥的横向振型和自振频率影响较小，对墩底弯矩和塔顶位移有一定影响，但最大相差在10%以内。不同体系之间支座剪力相差较大，塔梁固结、塔墩分离体系剪力是塔墩固结、塔梁分离体系剪力的1.5倍。

（2）采用双曲面支座能够有效减小两种体系下的结构截面内力响应。在主梁与桥塔间距足够时，双曲面支座对塔墩固结、塔梁分离体系的减震效果要好于塔梁固结、塔墩分离体系。

（3）采用双曲面支座进行减震以后，塔墩固结、塔梁分离体系的支座横向变形较塔梁固结、塔墩分离体系大，在减隔震设计时应注意主梁位移控制，防止发生主梁和桥塔的碰撞。