非平稳地震激励下结构动力可靠性方法对比研究

唐和生 郭雪媛 薛松涛

（1.同济大学结构防灾减灾工程系，上海200092；2.同济大学土木工程防灾国家重点实验室，上海200092）

0 引 言

结构动力可靠性是指结构系统在规定的时间间隔内，在随机动力荷载作用下完成其预定功能的概率。结构动力可靠性分析对基于性能的地震工程研究有着重要意义，为结构满足规定的性能指标提供了概率性的评估标准。

在结构动力可靠性问题中，当结构的某一与位移或速度响应相关的量（例如，绝对位移、相对位移、控制点的应力或应变等）超过给定阈值（确定性的常量）时，认为结构失效。这种基于规定时间段内累积失效概率的可靠性评估问题也被称为首次超越问题。地震从发生到结束是一个具有明显非平稳性的随机过程，即使是最简单的结构模型在非平稳随机激励下的失效概率解析解也无法获得，而Monte Carlo 模拟（MCS）方法作为目前唯一的近似精确方法计算成本极其昂贵。根据首次超越问题的基本理论，现有的非平稳随机过程激励下动力可靠性研究方法主要分为基于跨越率的方法和基于极值的方法。

Rice［1］首先提出了基于跨越率的方法，随后在跨越事件的发生服从Poisson 过程且统计独立假设的基础上，出现了大量研究。石少卿等［2］应用演变谱理论，通过求解多自由度线性体系在非平稳随机激励作用下的响应演变谱密度和时变均方响应解决了首次超越问题。Chaudhuri 和Chakraborty［3］在频域内进行随机动力分析，得到随机响应的功率谱密度函数，从而实现三维框架结构的动力可靠性分析。Barbato和Vasta［4］在改进后的Vanmarcke公式的基础上，推导了多自由度线性系统失效概率的封闭解。如上所述均为首次超越问题的近似分析方法，为了计算首次超越问题，还需进一步对首次超越事件的性质进行假定［5］。近年来，Andrieu-Renuad 等［6］提出一种PHI2 方法，引入一阶可靠度方法（FORM），将跨越率的计算转换为并联的静态问题并且得到了推广［7］。然而在实际工程中，结构动力可靠性分析为高度非线性且高维的隐式问题，这一类方法并不适用。因此，目前主要仍采用通过计算响应的功率谱密度函数［8］，结合首次超越破坏准则评估结构动力可靠性。

基于极值方法的关键在于识别极限状态函数的极值，在极值概率分布已知的情况下，时变可靠性问题可以转化为一个时不变问题。基于极值的方法在小失效概率问题中，往往需要进行大量的数值模拟［9］。为了提高计算效率，构建极限状态函数的代理模型方法已被广泛研究［10-11］，然而绝大多数代理模型由于存在维数诅咒而不适用于非平稳随机过程激励下的动力可靠性问题［12］。另一方面，研究者通过改进采样技术提高可靠性问题的计算效率。重要性采样［13］将样本从原始分布转移到失效区域，以便更有效地抽取小概率事件。子集模拟方法［14］通过引入适当的中间失效域，将原概率空间中的一个罕见事件的概率表示为条件概率空间中的序列事件概率的乘积，是近年来发展起来的一种计算小失效概率的高效可靠性分析方法［15］。

本文对目前常用的两种结构动力可靠性方法进行对比研究，探讨非平稳随机激励频谱特征及响应阈值对两种方法计算精度的不同影响，为结构动力可靠性问题提供更为通用的分析方法。

1 基于跨越率的动力可靠性计算方法

根据首次超越理论，对于双侧界限的结构动力可靠性问题，结构在规定时间段［0，T］内的动力可靠性为

式中：Pf(0，T)为累积失效概率；Y(t)为结构在非平稳随机激励下的响应；b是确定性阈值。

假定非平稳随机响应Y(t)为零均值高斯随机过程，相对于确定阈值b 的平均跨越率为νY(b，t)。通过对跨越率在时间段［0，T］内的积分得到累积失效概率的解析上限：

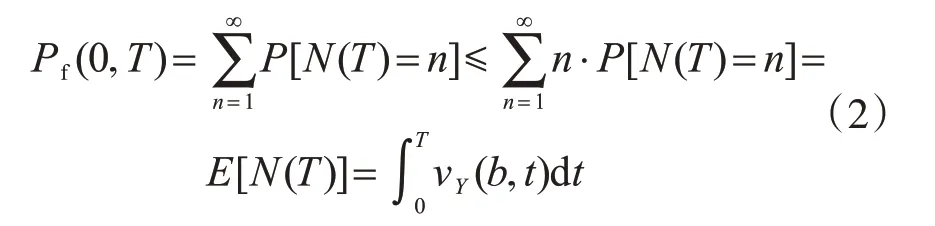
式中：E[...]为期望算子；N(T)为T时刻前跨越阈值的次数。

传统的Poisson 过程法基于任意两次交叉事件与其发生的时间统计独立，服从（无记忆）Poisson 过程假设。随着响应阈值提高和响应过程带宽的增加（如线性弹性系统中阻尼水平的增加），Poisson 过程法结果趋近于精确解。然而对于低阈值水平和/或窄带过程，Poisson过程法得到的是累积失效概率的保守值，将低估时变可靠性。

为克服Poisson 过程法的限制，Vanmarcke［16］认为交叉事件是成群出现的且各群之间相互独立，在双态Markov 过程假设的基础上提出了一种累积失效概率的改进估计：

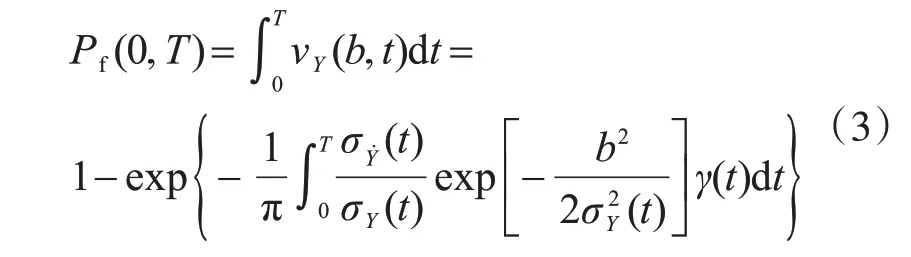
式中，σY(t)和σẎ(t)分别为随机过程Y(t)及其一阶导数过程的标准差，并且有

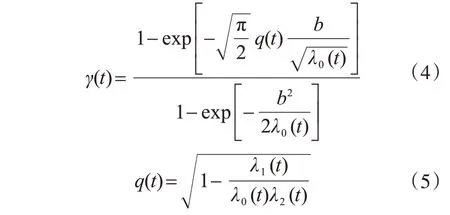
式中，λk(t)=2ωkSyy(ω，t)dω 为随机过程Y(t)的第k 阶谱矩，可进一步通过虚拟激励法对非平稳随机激励下f(t)的结构响应Y(t)进行求解。

针对工程中常见的非平稳随机过程，Priestley提出一种演变谱过程模型，表示为

式中，A（t，ω）是t与ω 的确定性调制函数；Z（ω）是一个正交增量过程。

如果用A（t）代替A（t，ω），则非均匀调制演变谱退化为工程中常用的均匀调制演变谱。构造如下形式的虚拟激励：

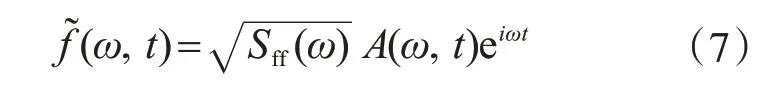
此激励在t 时刻产生的响应为y͂(ω，t)，可得任意响应的自功率谱函数计算式为

式中，*表示取复数共轭，相应的各阶谱矩为

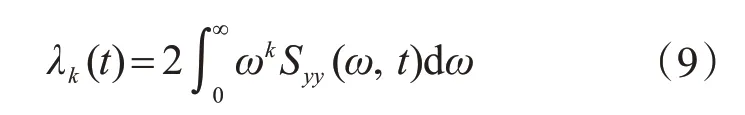
虚拟激励法将非平稳随机运动方程转化为确定性外荷载作用下瞬态响应方程，故可用Newmark-β 或Wilson-θ 法求解所关注物理量的虚拟响应并得到其时变功率谱密度及各阶谱矩。

尽管基于跨越率的方法在理论推导方面是合理的，但在实际应用中通常会受到一些限制。首先，交叉事件的独立性假设可能不成立，即使基于Markov 过程假设，动力可靠性的近似仍存在不可避免的误差；其次，对于复杂结构的动力可靠性问题，跨越率求解不仅技术难度大，而且计算成本极高。

2 基于极值的动力可靠性计算方法

基于极值的方法关注结构在规定时间段内的极限状态，由非平稳随机过程的演变谱表示理论，导出了非平稳随机过程模拟的一个谱表示方法，随机激励样本函数由余弦级数公式计算产生：

式中，Δω=ωu/N，ωu表示计算截止频率，超过ωu所对应功率谱能量可忽略不计；θk为在［0，2π］区间上均匀分布、相互独立的随机相位角。

因此非平稳随机过程激励可转换为一组随机变量θ=[θ1，...，θk]表示，动力可靠性问题被转化为与时间无关的一个隐式非线性高维可靠性问题。定义结构响应在时间段［0，T］内的极值变量：

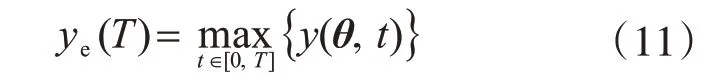
式中，θ为随机激励的一次样本。

极值法将结构的动力可靠性问题转换为对应等效极值分布的求解，则根据首次超越理论，累积失效概率可表达为

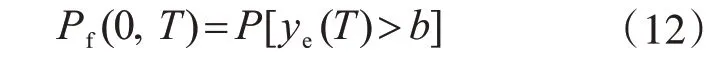
基于抽样的方法由于与维数无关且未对极限状态函数做任何假设，目前是解决高维可靠性问题的唯一可行方法，本文采用子集模拟方法提高计算效率。子集模拟方法的基本思想是通过自适应地引入m 层嵌套的中间事件，满足FE1⊃FE2⊃…⊃FEm=FE，将小失效概率转换成一系列相对较大的失效概率的乘积，即P(FEm)＜P(FEm-1)＜…＜P(FE1)。中间事件与目标失效事件FE 的 表 达 相 似，定 义 为FEi={ye＞bi，i=1，…，m}(b=bm＞…＞b2＞b1)。其中，m 为中间事件的总数。为自适应地确定中间事件，设定所有的中间条件概率为一常数p0，通常为兼顾准确性与计算效率取值p0∈[0.1，0.3]。

因此子集模拟方法首先根据不确定参数概率分布通过MCS 产生第一层随机样本，然后采用MCMC 方法不断产生中间事件相应的样本，最终子集模拟算法中的累积失效概率可表示为

3 数值算例

以单自由度结构为例研究非平稳随机过程频谱特征和响应阈值两个因素对基于跨越率和基于极值的动力可靠性计算方法精度的影响，并以样本数为106的MCS 方法计算结果作为准确值。单自由度结构受到非平稳地震激励时的运动方程为

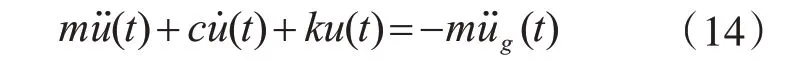
式中，m=20 000 kg；c 和k 分别为质量、阻尼和刚度；u(t)、u̇(t)和u(t)分别为位移、速度和加速度。

结构所受非平稳随机激励的调制函数为

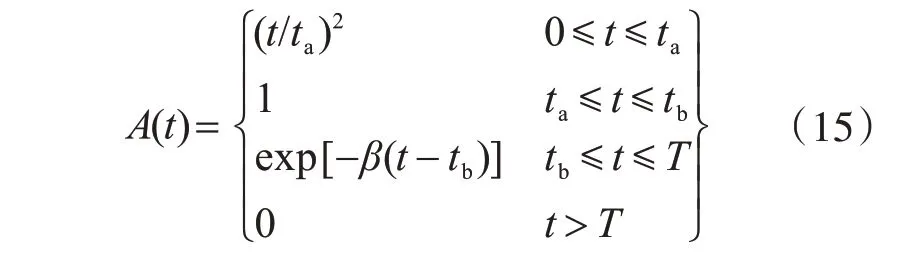
式中，T=20 s，ta=2.5s，tb=10 s，β=0.1，计算步长Δt=0.02 s，功率谱密度函数取Kanai-Tajimi模型：

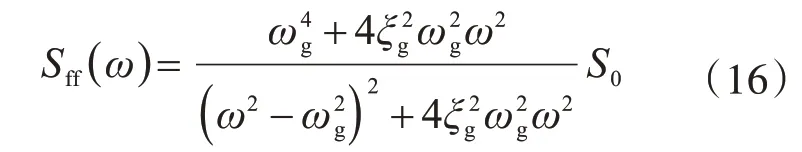
式中，ξg=0.6。

本研究中各计算工况见表1，各工况下功率谱密度函数如图1 所示。各工况中非平稳随机过程频谱特征ωg和S0取值满足非平稳随机激励所包含总能量相同。

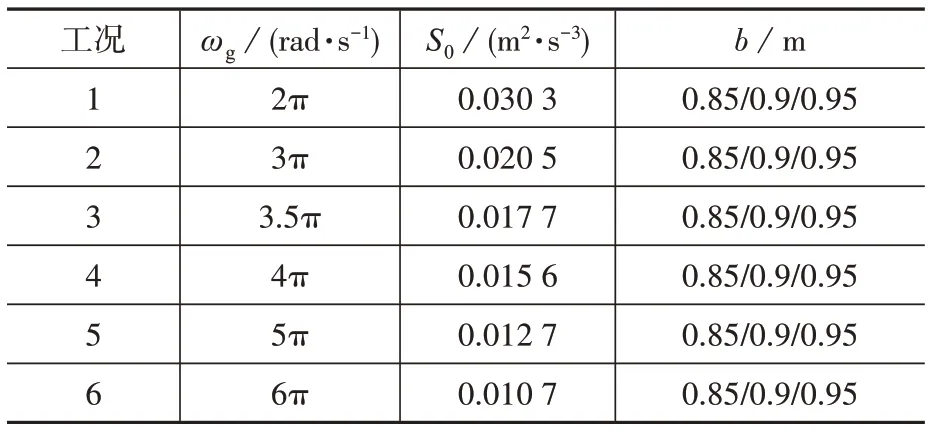
表1 计算工况Table 1 Calculation condition

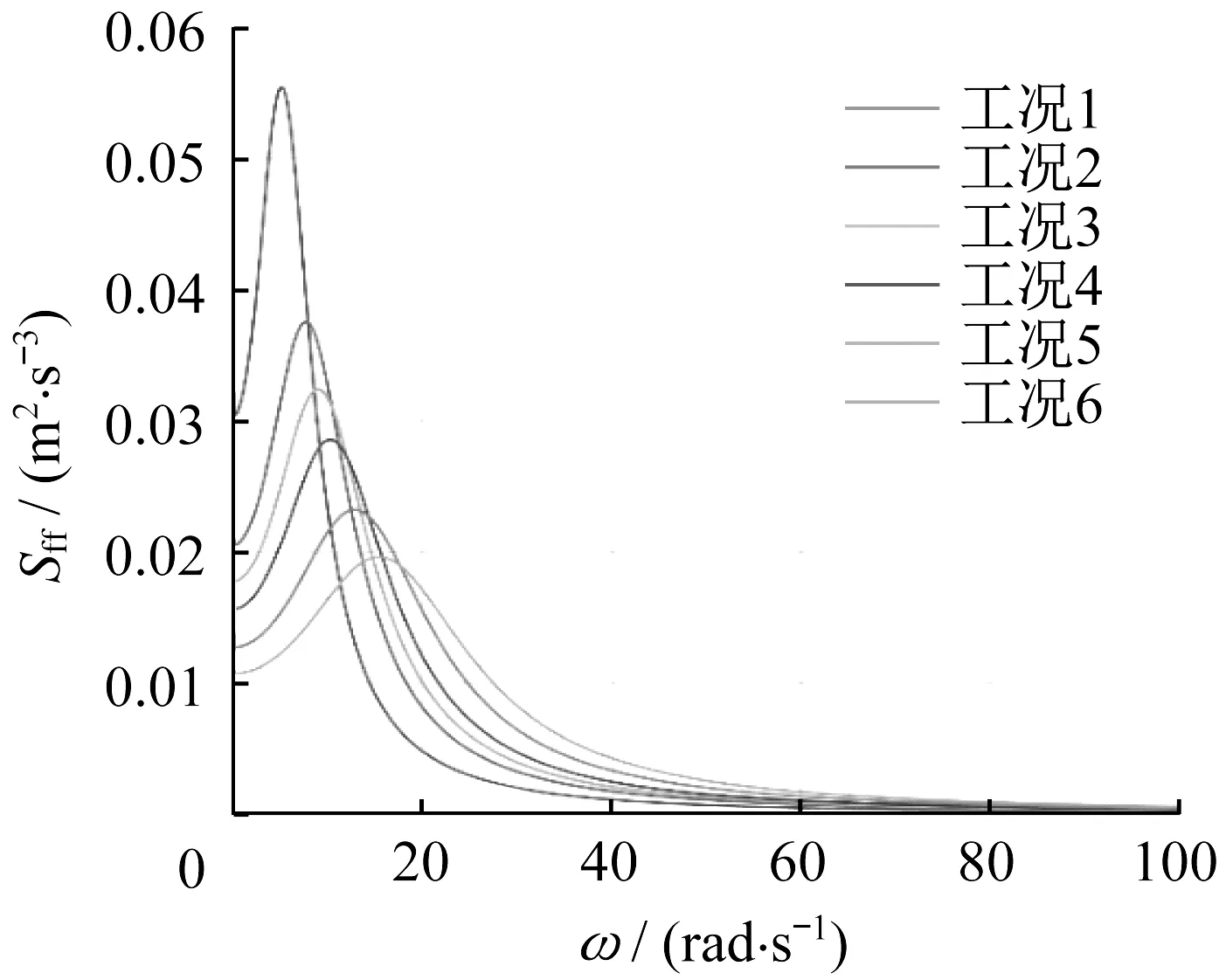
图1 功率谱密度函数Fig.1 Power spectral density functions

位移响应的绝对值超过阈值b 则认为结构失效，各工况下阈值分别设置为0.85 m、0.9 m 和0.95 m，用于比较响应阈值对动力可靠性计算结果的影响。对各工况分别采基于跨越率的方法、基于极值的方法和MCS 方法进行分析，其中基于极值的子集模拟算法中参数取值p0=0.3，第一层样本数为2 500。

4 结果分析

首先考虑非平稳随机激励的频谱特征对动力可靠性计算的影响。位移响应阈值均取b=0.09 m时，不同Kanai-Tajimi模型中的地基土卓越圆频率ωg对应6 个工况，采用基于跨越率的方法和基于极值的方法计算得到的累积失效概率随持时的变化曲线分别于MCS方法对比如图2所示。

由图2 可以看出，对于不同的非平稳随机激励频谱特征ωg和S0，基于极值的方法与基于跨越率的方法相比，计算结果都与MCS 方法更为相近，即计算精度更高；随着失效概率的增大，基于跨越率方法的误差逐渐减小，其中工况3、工况4的跨越率方法累积失效概率曲线与MCS 方法几乎重合；在计算效率方面，以工况3 为例，基于极值的方法所需时程分析总数为21 265 次，约为MCS 方法计算量的2.13%，计算效率显著提高，而基于跨越率的方法本质为求数值解计算成本极低。

同时考虑非平稳随机激励频谱特性及响应阈值两个影响因素，图3 及表2、表3 为两种方法计算各工况在T=20 s 的累积失效概率与MCS 方法的相对误差。结果表明：①非平稳随机激励的频谱特征对基于跨越率的方法有明显影响，当Kanai-Tajimi 模型中的地基土卓越圆频率ωg与结构圆频率ωS=3.704πrad/s 差距增大，计算精度显著下降；②响应阈值对功率谱方法的准确性也有一定影响，随响应阈值的降低，计算精度有所改善，且基于跨越率的方法对可靠性预测大部分偏保守；③基于极值的方法对随机激励的频谱特征和响应阈值并不敏感，且由于样本抽取的随机性，误差有微小变化，表明基于极值的方法在各种情况下均保持较高的计算精度。

5 结论

本文对非平稳随机激励下结构动力可靠性分析的两种常用方法进行了对比研究，分析了非平稳随机激励频谱特征及响应阈值两种因素对于动力可靠性方法计算精度的影响。主要结论如下：

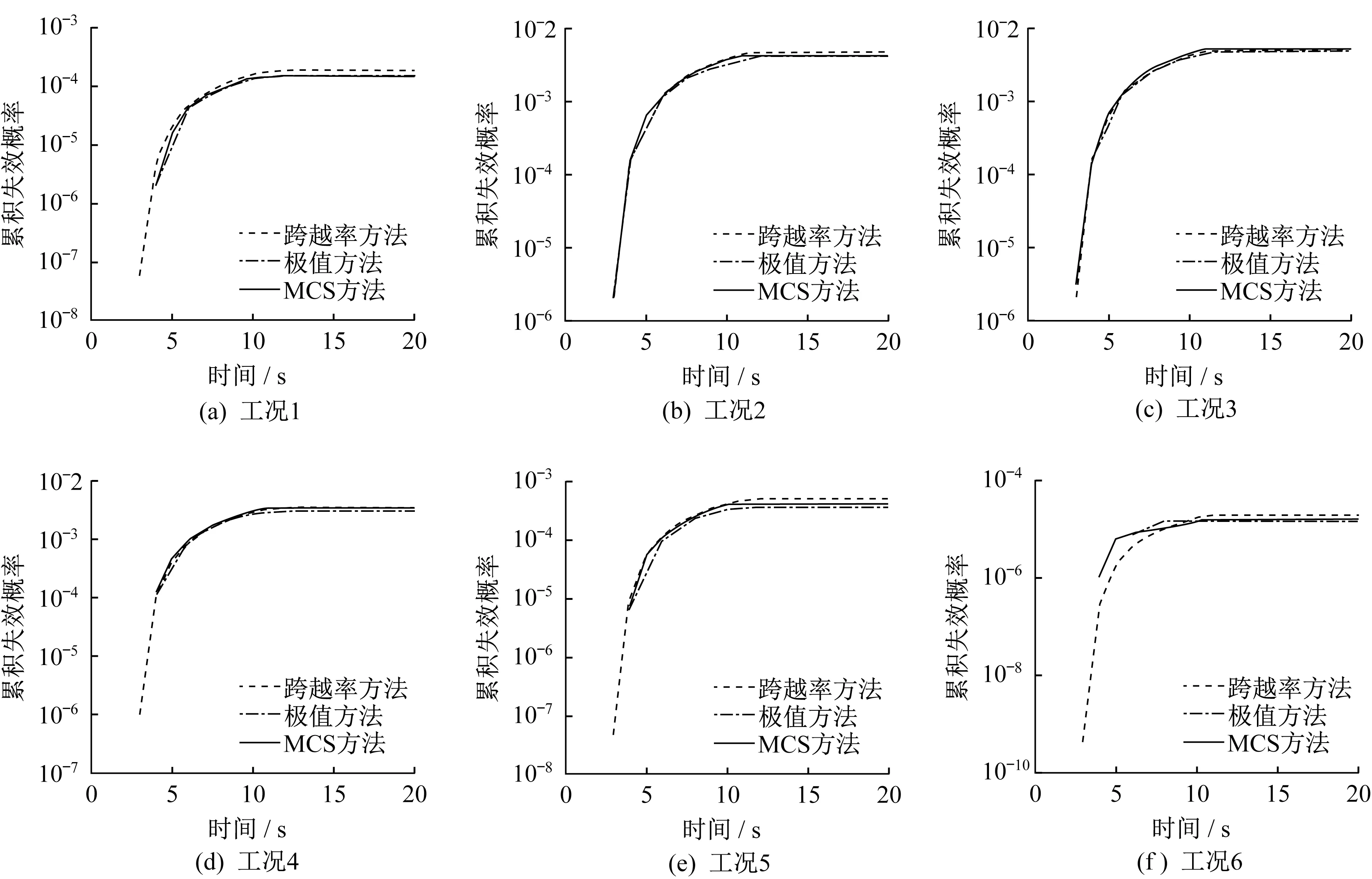
图2 b=0.09 m时累积失效概率Fig.2 Cumulative probability of failure for b=0.09 m

图3 20 s时相对误差对比Fig.3 Comparison of relative error at 20 s

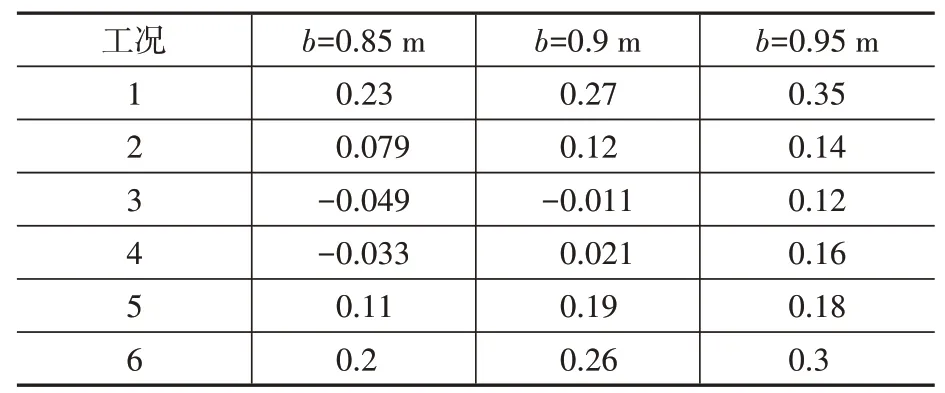
表2 T=20 s跨越率方法相对误差Table 2 Relative error of out-crossing rate based method at 20 s

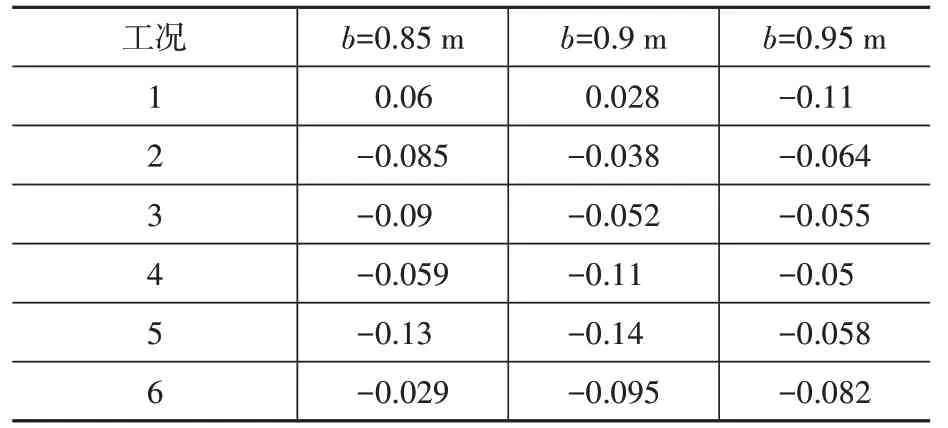
表3 T=20 s极值方法相对误差Table 3 Relative error of extreme value based method at 20 s

（1）基于跨越率的方法在计算累积失效概率时，受到非平稳随机激励的频谱特征影响显著，当Kanai-Tajimi 模型中的地基土卓越圆频率与结构圆频率接近时，计算精度显著提高。

（2）随着定义失效事件的响应阈值提高，基于跨越率方法的动力可靠性计算误差逐渐增大。响应阈值和非平稳随机激励频谱特征对于基于跨越率方法的精度影响，本质均表现为该方法在小失效概率问题中误差较大。

（3）基于极值的方法与基于跨越率的方法相比，在各种工况中均具有良好的精度，不受到非平稳随机激励频谱特征和响应阈值的影响。并且作为一种本质为数值模拟的方法，与传统的MCS 方法相比具有相当高的计算效率。因此，基于极值的方法是一种具有更广泛适用性的动力可靠性分析方法。