基于预测理论的投资组合选择模型的研究

孙冲，吴天庆，王虹

(1.陆军炮兵防空兵学院,安徽 合肥 230000；2.宿迁学院 文理学院,江苏 宿迁 223800)

1952年，Markowitz[1]首次提出了M -V投资组合模型，该模型为研究现代投资组合选择理论奠定了基础.但是，市场中存在诸多不确定性问题，如股票价格、换手率等.为此，Zadeh[2]提出了模糊决策理论.随后，一些学者基于模糊决策理论对模糊收益下的投资选择模型进行了研究[3-7].这些研究结果在一定程度上弥补了传统M -V模型的不足，但利用数学期望值对预期收益率进行测度时仍存在个人主观性较强的问题.对此，本文利用区间模糊数的整体GM(1,1)预测模型，对股票的收益率和流动性等进行预测，得到相应的预测区间模糊数；并在此基础上，基于区间模糊数构造一种投资组合选择模型，并以实例分析验证该模型的有效性.

1 区间模糊数的相关知识

定义1[8]在论域U上给定一个映射A∶U→[0,1]，即μA(μ),则称A为U上的模糊集，称A(μ)为A的隶属函数(或者称μ为A的隶属度).Γ为所有的模糊数的集合.

定义2设A∈Γ(U)，任取γ∈[0,1]，记[A]γ={t∈R:A(μ)≥γ}=[a1(γ),a2(γ)].当γ>0时,称[A]γ为A的γ-截集，其中γ为阀值或置信水平，ai(γ) (i=1,2)为[A]γ的左右端点.

定义3[9]若a≤b且a,b∈R，则A=[a,b]为区间数，其中a为区间数的下界，b为区间数的上界.当a=b时，区间数为清晰模糊数.

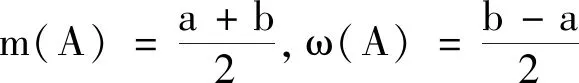
定义5设A=[a1,b1]，B=[a2,b2]，则：

1)A+B=[a1+a2,b1+b2];

2)A-B=[a1-b2,b1-a2];

3)A×B=[min(a1a2,a1b1,a2b1,b1b2),max(a1a2,a2b1,a1b2,b1b2)];

2 区间模糊数的整体预测

定义6[6]设模糊数序列x(0)(t)=[x(0)(1),x(0)(2),…,x(0)(n)]，则x(0)(t)的一次累加序列为

上述一次累加序列的白化背景值序列为

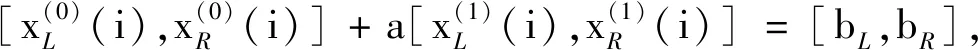
根据定义7可得区间模糊数GM(1，1)模型的预测公式，为:

(1)

3 建立含交易成本的模糊组合选择模型

在股票投资中，股票的流动性是不可忽略的.流动性主要包括宽度、深度、及时性以及弹性等方面.本文利用换手率度量流动性，并建立如下含有流动性约束的M -V模型：

(2)

其中:ci为第i个股票的交易成本的比率；Ri为第i个股票的预测收益率；xi为第i个股票的投资比例，记x=(x1,x2,…,xn)T；li为第i个股票的换手率；V=(vi j)n ×n为协方差阵.

利用区间模糊数的预测公式(1)可得到股票预期收益率和流动性的相应区间模糊数，进而根据区间模糊数可将模型(2)转换为含有区间模糊数的M-V模型(3)，利用模型(3)即可实现对股票的收益率和流动性进行测度.

(3)

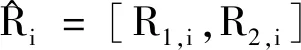
利用区间数的中点和半径可将模型(3)转化为如下双目标规划模型:

minf(x)=〈m(f(x)),ω(f(x))〉；

(4)

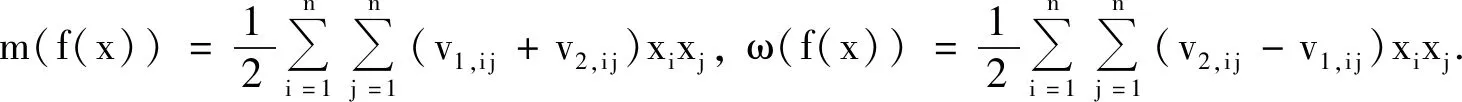
假设参数λ表示投资者的风险偏好，则利用系数λ可将模型(4)转化为如下单目标规划模型:

(5)

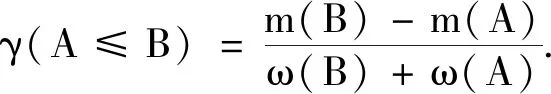
根据定义8对模型(5)中的区间数约束条件进行优化可得如下结论：

利用结论1和结论2，可将模型(5)转化为如下含有单目标规划的模型:

(6)

其中:0≤λ,α≤1.

4 实例分析

本文以2018年9月至2019年9月上交所中的5种股票为例进行实例分析.对5种股票的每月收盘价格和换手率进行预测后得到如下5种股票的预测收益率的区间数、元素为区间数的协方差阵和换手率的区间数：

1)预测收益率的区间数为：

2) 元素为区间数的协方差阵为：

3) 换手率的区间数为：

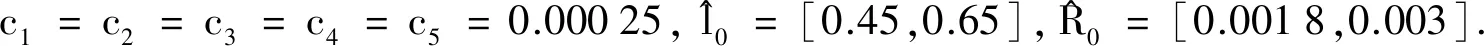
表1 不同参数下的投资策略