直接空冷机组最佳背压计算及分析

李国庆，徐 威，王 永，陈雅丽

(1.中电华创(苏州)电力技术研究有限公司，江苏 苏州 215123；2.安徽芜湖发电有限责任公司，安徽 芜湖 241000；3.大同电力高级技工学校，山西 大同 037039)

0 引 言

直接空冷机组具有汽轮机排汽压力高、空冷风机耗电量大、背压波动幅度大等显著特点。机组能否安全稳定、经济运行直接受到机组背压高低的影响[1]。同时，机组运行背压易受环境因素干扰，存在夏季机组背压高，负荷受限，冬季空冷换热面冻结的现象[2-3]。

直接空冷系统中，降低汽轮机的排汽压力可以增加机组的发电功率，但并不是冷凝器背压越低越好。在一定的环境温度和冷凝流量下，要想使得凝汽器背压降低，只能通过提高迎面风速，即增大冷却风量来实现，而增大冷却风量会导致风机的功耗升高。因此存在一个被称为“最佳背压”的凝汽器压力，在该压力情况下，提高风量降低冷凝器排汽压力所多出的电功率ΔPe与风机提速导致多消耗的电功率ΔPfan之差达到最大值。所以，确定机组的最佳背压有利于实现机组的节能降耗以及优化机组运行[4-5]。

将某电厂600 MW机组作为算例，计算不同运行工况下机组最佳的背压情况，以分析环境温度和当前运行背压对最佳背压的影响。

1 最佳背压的计算方法

设定凝汽器背压为pc，最佳背压为pc,op，两者相等时汽轮机功率P相对最大，其定义式可写为

P|pc=pc,op=max(ΔPe-ΔPfan)

式中：ΔPe为汽轮机的微增功率；ΔPfan为风机提速导致多消耗的电功率。

图1为凝汽器最佳背压的确定示意图[6]。

因此，计算直接空冷机组冷凝器最佳背压就转换为计算汽轮机的微增功率ΔPe以及风机提速导致多消耗的电功率ΔPfan。

1.1 机组微增功率计算

工程上用来计算由排汽压力改变而导致机组功率变化主要有4种方法，不同方法根据机组各有应用。结合某电厂600 MW的直接空冷系统工作特性，选择等效热降法进行计算。

1.1.1 等效热降法

等效热降法是以回热系统的热力平衡为基本原理的一种计算方法，这种计算方法与其他方法的区别在于对整个热力系统的部分进行分析时，将重点放在整体中出现变化的局部，进一步分析出因为部分变化而引起的整个空冷机组的影响。

对于纯凝汽式机组，由于不存在抽汽等损失，蒸汽通过汽轮叶片所减少的焓值就转换成对机组的做功，所以对于单位质量蒸汽，有：

H=h0-hc

式中：h0为蒸汽的初始焓值，kJ/kg；hc为乏汽的焓值，kJ/kg。

而对于具有回热的机组，单位质量蒸汽经过机组叶片的做功为

H=(h0-hc)-α1(h1-hc)-…-αz(hz-hc)

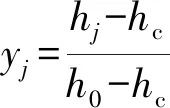
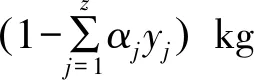
1.1.2 排汽压力变化的等效热降计算

如果汽轮机的背压发生改变，其对发电系统功率的影响主要体现在两方面，其一为乏汽的焓改变导致整个汽轮机有效焓的变化值ΔH01；另一个则为由于冷凝循环水温度的改变导致最后一级低温加热器的蒸汽抽汽份额出现的变化值ΔH02。排汽压力做功分析如图2所示。

图2 排汽压力做功分析图

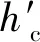
另外，凝结水温度变化引起机组内蒸汽做功量的变化。根据等效热降原理，就相对于蒸汽产生的αnnΔτn焓值变化。那么此时抽汽份额发生改变导致机组做功的变化为

ΔH02=αnnΔτnη′1

式中：αnn为流经低加的凝结水份额；Δτn是最后一级的加热器凝结水焓的上升值，kJ/kg；η′1是机组背压改变之后末级低压加热器的抽汽效率，不同的加热器有不同低加抽汽效率。

通常加热器可以分为疏水自流型加热器和汇集型加热器，若为前者，则可以按照式(1)得出低加抽汽效率[7]：

(1)

式中：η1为运行工况下1号加热器的抽汽效率,%；H′1为变工况下抽汽焓降，kJ/kg；q′1为变工况下1级抽汽在加热器中的放热量，kJ/kg；H1为第1级抽汽的焓降，kJ/kg。

而如果加热器选择后者，那么可以按照式(2)计算抽汽效率：

(2)

式中：q1为运行工况下1级抽汽在该加热器中的放热量，kJ/kg。

所以因为汽轮机背压变化而引起的单位质量蒸汽焓值改变为

ΔHi=ΔH01-ΔH02

则由机组排汽压力改变引起蒸汽焓降改变为

如果汽轮机的主蒸汽量是D0，则机组背压改变时，汽轮机电功率的改变量能够根据式(3)得出：

ΔPe=D0(ΔH02-ΔH01)ηmηg/3.6

(3)

式中：ηm为机械效率；ηg为发电机效率。

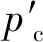
(4)

式中：hjq是低压缸入口蒸汽的焓，kJ/kg；Δh′jr是变工况运行结束低压缸的焓降，kJ/kg；ηelep是低压缸的额定效率，%。

变工况运行汽轮机低压缸的排汽焓为

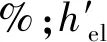
蒸汽的干度通常根据式(5)计算：

(5)

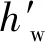
对于汽轮机低压缸末级排汽损失的计算，需要先知道变工况运行条件下的机组乏汽的比体积以及其体积流量，这样按照机组生产时绘制的排汽损失过程曲线图就能够得出汽轮机低压缸最后一级的在排汽时的各种损失。

变工况运行条件下乏汽的比体积计算式为

v′=v′sX′

式中；v′s为变工况机组在相同的压力条件下干饱和蒸汽的比体积，m3/kg。

1.1.3 抽汽等效热降计算

第j级回热抽汽量降低1 kg所排挤蒸汽的做功改变值也就是所谓的抽汽等效热降Hj，该定义仍将其下一级抽汽部位抽汽份额的改变包括在内。确定Hj是比较容易的，有一定的规律可循，可归纳成下式：

式中：Am表示单位疏水在m级加热器的放热量，Am取γm或τm；γm为单位疏水在m级加热器的放热量；τm为第m级加热器中单位凝结水的焓升；若加热器型式为汇集式，Am取τm，若加热器型式是疏水自流式，则用γm取代Am，二者单位均为kJ/kg；Hm为第m级等效热降，kJ/kg；qm为单位质量抽汽在第m级加热器中放热量，kJ/kg。

抽汽效率ηj的定义为抽汽等效热降Hj和造成Hj出现而送入的热之比。一旦知道了Hj，相对应的抽汽效率ηj能够直接代入式(6)快速得出：

(6)

1.2 空冷风机耗功计算

如果所研究的风机与某定性风机是属于同种类型或者几何尺寸成比例的情况下，则能够按照相似定理计算得出环境温度变化时不同转动速度下风机群的功耗[9]：

(7)

式中：NG是风机群的总耗功功率，kW；Ni是单台风机的实际耗电功率，kW；N0是在设计转动速度下风机的电耗功率，kW；ρi是实时的大气密度值，kg/m3；ρ0是测定额定工况下大气的密度值，kg/m3；qvi为不同风机转速下的风量，m3/h；qv0为额定转速下风机的最大风量，m3/h。

2 计算结果

某电厂600 MW空冷机组抽汽相关参数见表1，风机相关数据(30 ℃、30 kPa工况)见表2。

2.1 不同工况

根据上述理论及数据，计算不同运行工况下该机组的最佳背压。

1)运行工况1：此工况下环境温度为22.53 ℃，汽轮机的运行负荷为350.2 MW，排汽压力为10.28 kPa，总的凝汽流量为197.47 kg/s。经运算可知最佳背压是12.076 kPa，此刻的迎面风速为1.83 m/s，是设计运行工况条件下风速的90.95%(即1.83/2.012)。功率增量与机组背压关系如图3所示。

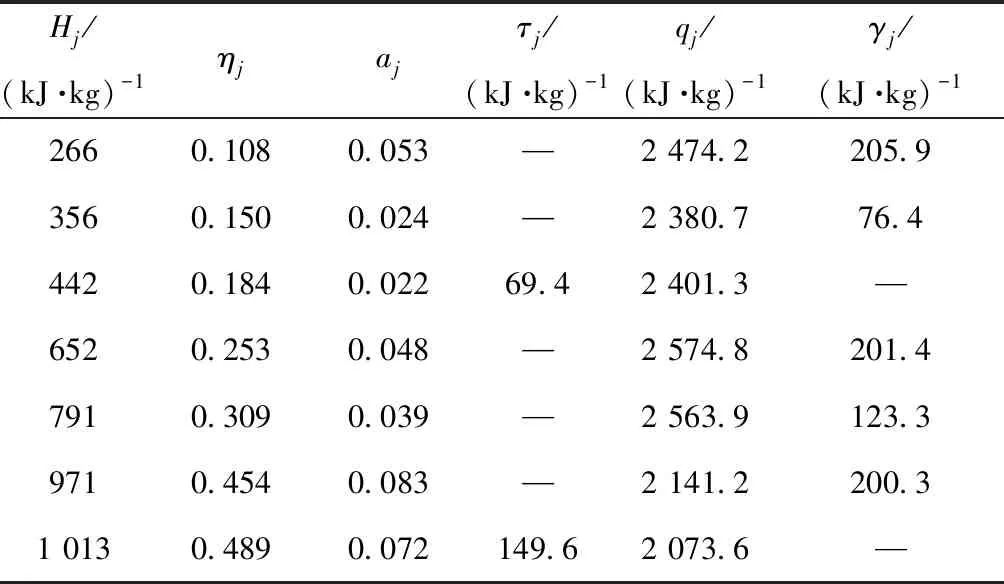
表1 抽汽等效热降以及热力系统参数Table 1 Equivalent heat drop of extraction steam and parameters of thermal system

表2 空冷风机数据Table 2 Data of air-cooled fan

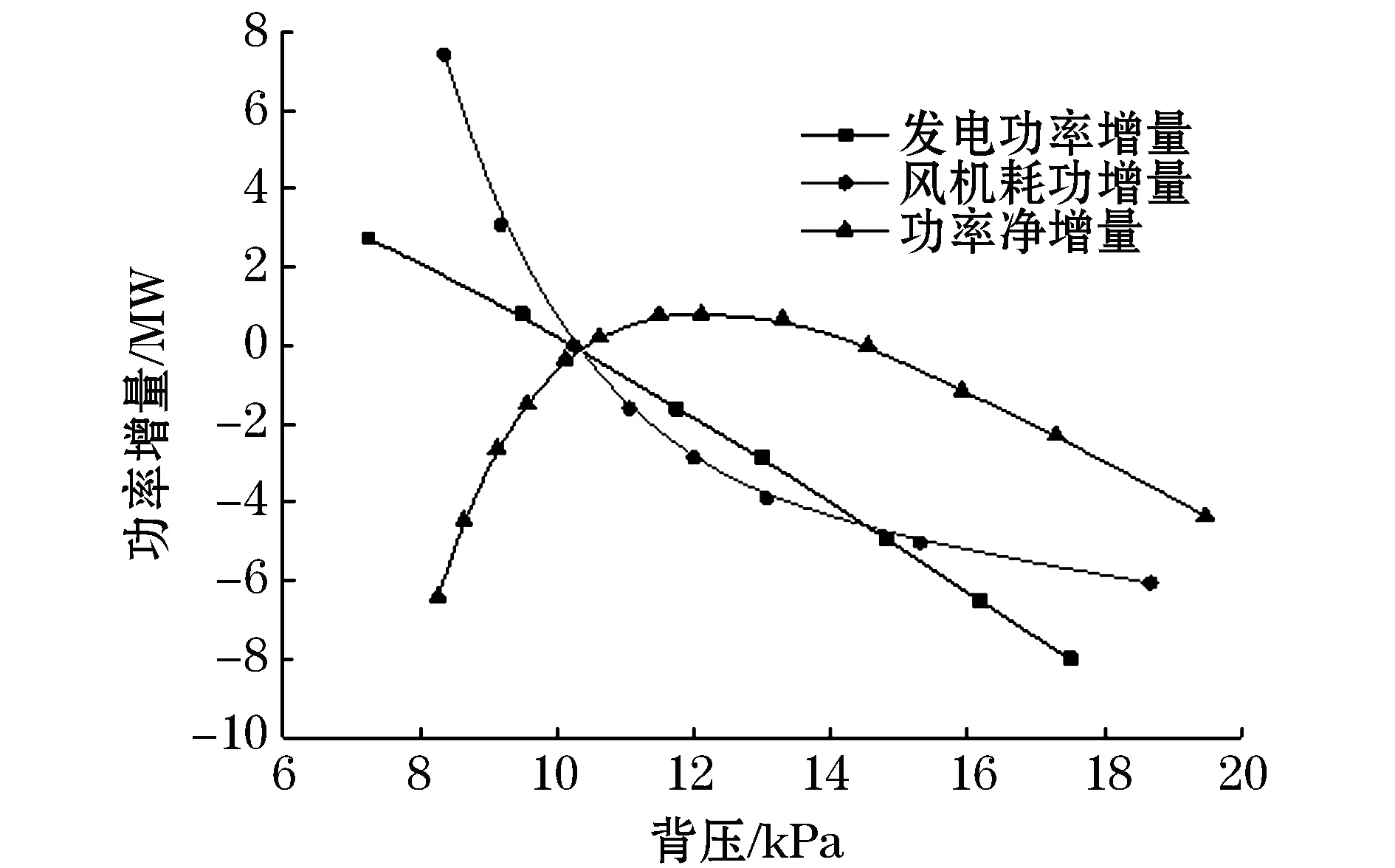
图3 350 MW工况下的最佳背压

2)运行工况2：环境温度为25.73 ℃，汽轮机的实际负荷为399.07 MW，此时工作的背压为16.04 kPa，总的凝汽流量为240.37 kg/s。此工况下功率增量与背压关系如图4所示，计算可得该工况下机组的最佳背压为14.868 kPa，此刻的迎面风速为2.08 m/s，是设计运行工况条件下风速的103.3%。

3)运行工况3：环境温度为27.47 ℃，汽轮机的实际负荷为501.17 MW，此时工作的背压为21.63 kPa，总的凝汽流量为283.24 kg/s。经过运算可知该运行工况下的最佳背压为18.987 kPa，此刻的迎面风速为2.495 m/s，是设计运行工况条件下风速的124%，在此工况中汽轮机各部分功率增量与汽轮机背压曲线如图5所示。

4)运行工况4：环境温度为25.85 ℃，汽轮机的实际负荷为551.08 MW，此时工作的背压为23.13 kPa，总的凝汽流量为311.83 kg/s。可知该运行工况下的最佳背压为17.985 kPa，对应的迎面风速是2.46 m/s，占设计运行工况条件下风速的122.26%。图6为功率增量和汽轮机背压关系。

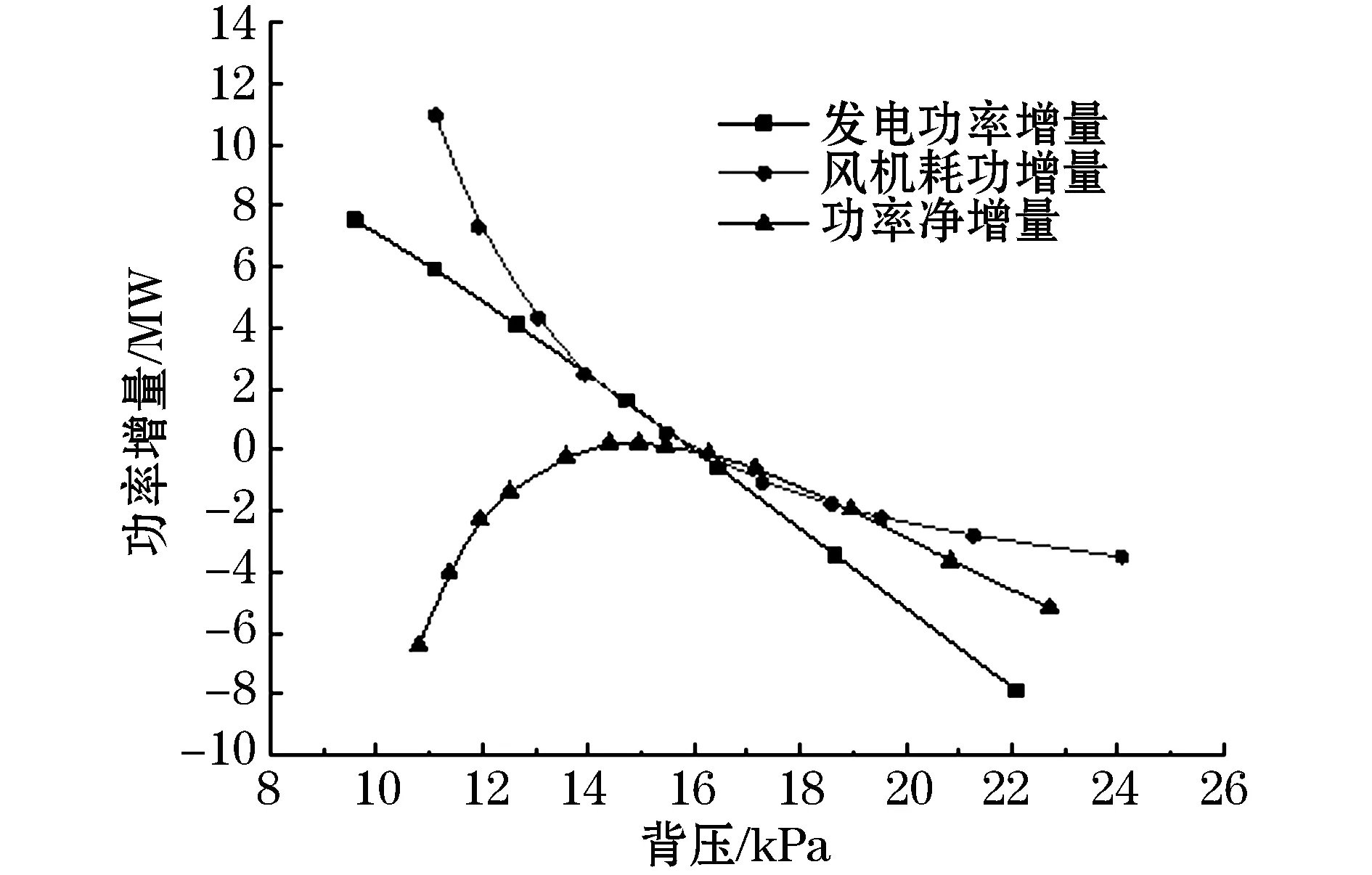
图4 400 MW工况下的最佳背压

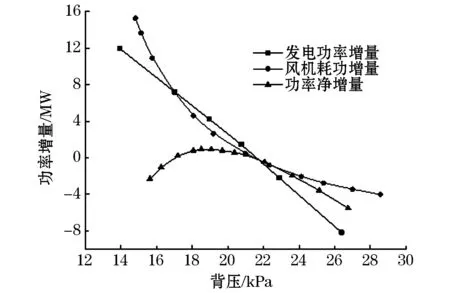
图5 500 MW工况下的最佳背压

2.2 影响因素分析

85%THA负荷工况下周围环境温度对直接空冷机组运行最佳背压以及最佳风机频率的关系如图7所示。随着环境温度升高，机组最佳背压逐渐增大，且风机的最佳工作频率同样会上升，但是当风机负荷达到峰值时风机频率便不再变化。

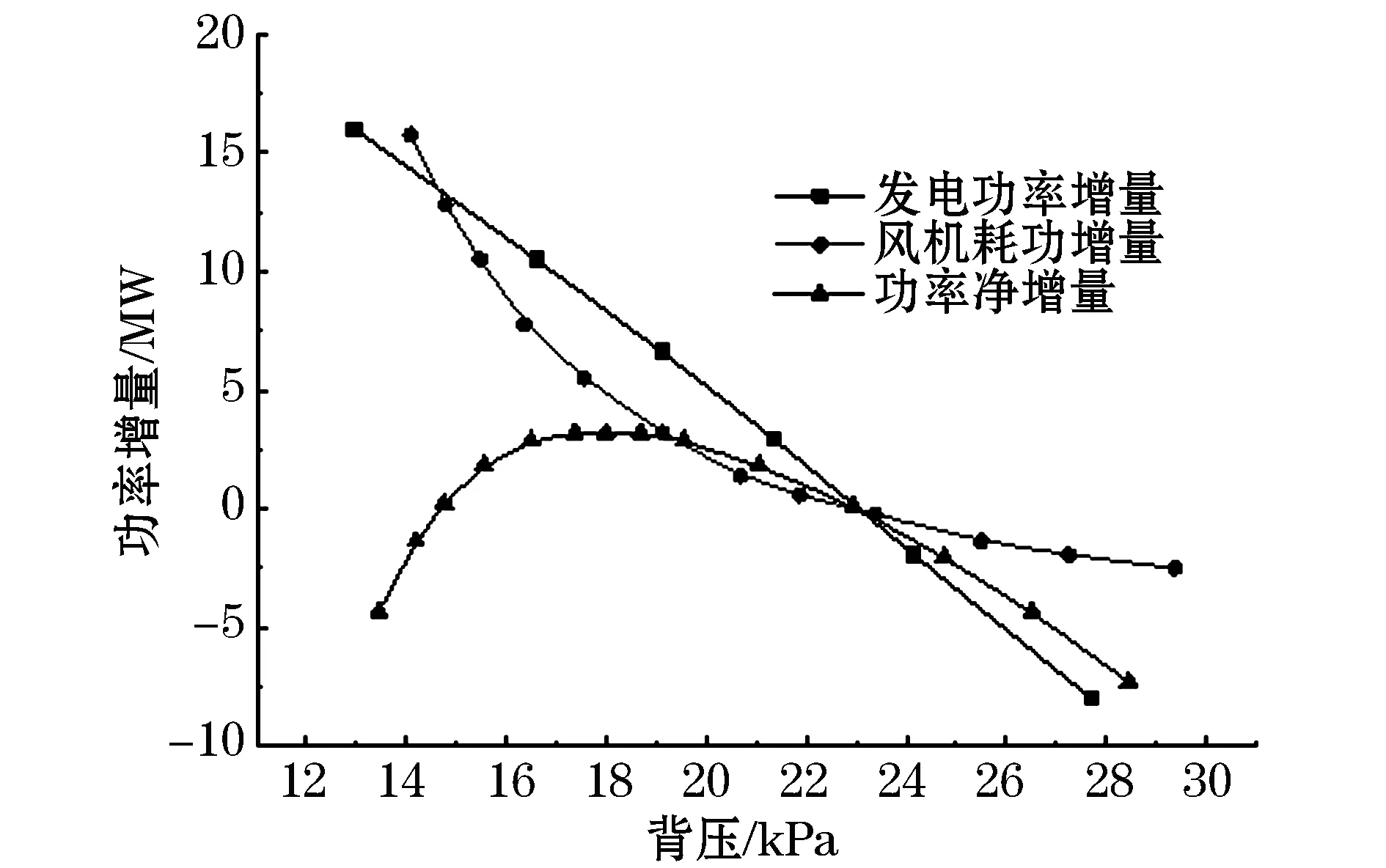
图6 550 MW工况下的最佳背压

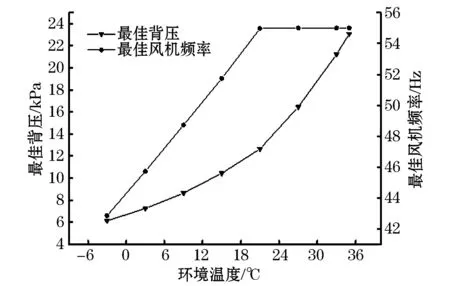
图7 85%工况下，环境温度对最佳背压的影响

在环境温度以及机组的凝汽流量保持不变的情况下，通过使当前背压变化，分析其给汽轮机最佳背压确定带来的影响，根据程序计算得出的结果绘制曲线，如图8所示。能够发现，直接空冷系统的功率改变的数值是由当前背压决定的，但是当前背压无论为何值，机组的最佳背压仍然不会改变。因此，当前背压对机组最佳背压基本上不会起作用。

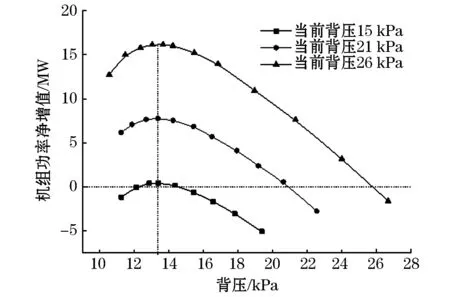
图8 当前背压变化，背压与功率改变值之间的关系

3 结 语

1)不同运行工况下机组的最佳背压不同，因此在机组实际运行过程中要优化机组背压，使机组的性能达到最高。

2)因轴流式风机的负荷运行区间有一定范围，而一旦风机频率上升至某一定值后，则无法仅仅依靠改变送入的风量来调节汽轮机的排汽压力，而且此时如果周围温度继续上升或是机组的负荷再一次增加，汽轮机的排汽压力会立即增大，为防止事故发生、使机组能够稳定工作，要启用喷水降温或者使机组的负荷减小。

3)机组当前运行的背压不会影响机组的最佳背压，但是会给机组的功率净改变量带来变化，对优化机组运行、节能降耗有重要意义。

4)机组的最佳背压受环境温度作用较大，随着环境温度的增加而上升，因此需要避免环境温度带来的影响，并且对其加以利用以优化机组运行。