察“构”观“式”抓本质变式同构妙转化

安徽省池州市第一中学(247000) 吴成强

所谓同构变换，就是通过巧妙变形，使式子两边的结构相同，具有对称美，然后再构造新的函数;或者使式子的局部结构相同，再通过换元，使复杂的式子变得简单，从而使问题求解变得简单.同构解题，观察第一.要有敏锐的观察力，善于察“构”观“式”抓本质，发现式子的结构特征，利用有关公式和法则实施巧妙变形，化成“同构”式，再通过构造函数或换元，使问题巧妙求解.同构变换对创新能力有较高要求，能很好地锻炼我们的创新能力，增强思维的广阔性.同构的技巧性很强，方法灵活，常用的同构方法主要有: ①利用指数对数恒等式实施同构，问题求解可“妙杀”之.②利用三角变换实施同构，解法巧妙.3○加减同构，在同构的过程中“加减配凑”，从而完成同构.4○乘除同构，在同构的过程中“乘除配凑”，从而完成同构.5○局部同构，即在同构的过程中，将函数的某两个或者多个部分构造出同构式，再巧妙换元.6○整体同构，即使式子两边结构相同，便于构造函数巧妙求解.7○放缩同构，即通过巧妙放缩后再同构，使问题求解变得非常简单，对思维有很大的启发.

一、利用指数对数恒等式实施同构变换

指数对数恒等式:alogaN=N(a ＞0,a /=1,N ＞0)，利用指数对数恒等式，可以巧妙进行同构变换，使方程两边的结构相同，从而可以构造一个函数，再利用函数的性质，把复杂问题化为简单问题，这种方法让人大开眼界，令人赏心悦目.

例1已知正实数x满足求m的值.

解由已知得:令f(x)=x ·ex，则f(x)=又易知f(x) 在(0,+∞) 上单调递增，所以x=即x=-lnx，令g(x)=x+lnx，易知g(x)在(0,+∞)上单调递增，所以存在唯一x0∈(0,+∞)，x0=即lnx0=-x0，m=所以m=1.

评注本题通过指数对数恒等式，结合函数的单调性，将复杂的方程化为等价的简单方程x=-lnx，这一转化真可谓神来之笔，也揭示了看似复杂繁琐的方程(或式子)，通过去粗取精，去伪存真，抽丝剥茧，由表及里，揭示本质，其实就是一个非常简单方程(或式子)，也使我们进一步感受数学魅力之所在，式子变形之巧妙.

例2已知λeλx≥lnx(λ ＞0)恒成立，求λ的范围.

解因为x ＞0，所以λxeλx≥xlnx=elnx ·lnx，设f(x)=xex，易知f(x)在[0,+∞)上单调递增，原不等式化为f(λx)≥f(lnx).

①若0＜x ＜1，则λeλx ＞0＞lnx成立.

②x≥1 时，lnx≥0，所以λx≥lnx，λ≥令则所以x ∈[1,e)时g′(x)＞0，x=e 时g′(x)=0，x ∈(e,+∞)时g′(x)＜0，所以x=e 时g(x)取最大值，g(x)max=g(e)=所以

评注将已知不等式两边同乘以正数x，得到一个新的不等式λxeλx≥elnx·lnx，这个新的不等式是通过指数对数恒等式进行同构变换，从而便于构造函数，再利用函数的性质巧妙求解，这种解法也是让人深受启发.

二、利用三角变换公式实施同构变换

与三角函数有关的问题，往往要利用三角变换公式实施同构变换，使三角函数名称相同，式子两边的结构相同，再通过构造函数，使问题巧妙求解.

例3已知定义在R 上的函数f(x)，其导函数为f′(x)，若f(x)+f(-x)=cosx，且当x≤0 时，则不等式的解集为( )

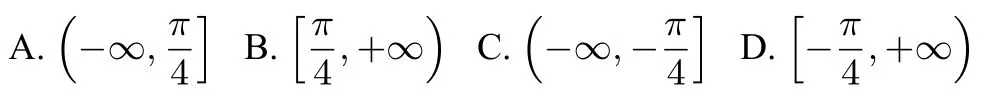
解由得，f(x)+即令g(x)=f(x)-则g(x) ≥且有当x ∈(-∞,0]时，g′(x)=f′(x)+所 以函数g(x) 在(-∞,0] 上单调递增，又f(x)+f(-x)=cosx，所以于是g(-x)=-g(x)，g(x)为奇函数，所以g(x)在R 上单调递增，由故选B.

评注本题就是通过三角变换使不等式两边的结构相同，从而可以进行同构变换，这种解法的技巧性比较强，需要我们善于发现式子的结构特征，从而有目标地进行式子的变形.

三、对式子的局部实施同构变换

局部同构，即在同构的过程中，我们可以将函数的某两个或者多个部分构造出同构式.然后再把同构的式子用一个新的变量代换，使式子变得简单，从而使问题巧妙求解.

例4已知f(x)=(ax+lnx+1)(x+lnx+1) 与g(x)=x2的图像至少有三个不同的公共点，则实数a的取值范围是( )

解由f(x)=g(x)得，令t=，(a+t)(1 +t)=1，a=-t，令h(t)=- t，h′(t)=--1＜0，所以h(t) 在(-∞,-1) 上单调递减，在(-1,+∞) 上单调递减，φ(x)=，φ′(x)=，由φ′(x)＞0 得0＜x ＜1，由φ′(x)＜0 得x ＞1，所以φ(x)在(0,1)上单调递增，在(1,+∞) 上单调递减，φ(x)max=φ(1)=1，且时，φ(x)＞0，因为至少有三个不同零点，所以0＜t1＜1，t2＜0，所以

评注本题通过巧妙变形，把式子中所含的变量局部同构成，然后通过换元，把原本复杂的式子化成简单的式子，从而使问题巧妙求解.

四、对式子两边整体实施同构变换

有的式子两边的结构已经相同，这时就是要善于发现式子两边结构特征，要能够透过现象看本质.有的式子需要经过适当变形，才能使式子两边的结构相同.处理这类问题的最好办法就是实施同构变换，构造函数，再利用函数的性质巧妙求解.

例5已知函数f(x)=(a+1)lnx+ax2+1，其中a ＜-1，如果对任意x1,x2∈(0,+∞)，x1/=x2，且|f(x1)-f(x2)|＞4|x1-x2|，求a的取值范围.

解f′(x)=+2ax=，因为a ＜-1，x ＞0，所以f′(x)＜0，f(x)在(0,+∞)上单调递减，不妨设0＜x1＜x2，则f(x1)＞f(x2)，所以原不等式可化为f(x1)-f(x2)＞4(x2-x1)，即f(x1)+4x1＞f(x2)+4x2，令g(x)=f(x)+4x，所以g(x1)＞g(x2)，所以g(x) 在(0,+∞) 上单调递减，g′(x)=即2ax2+4x+a+1 ≤ 0 对x ＞0 恒成立，令h(x)=2ax2+4x+a+1，因为a ＜-1，所以h(0)=a+1＜0，对称轴所以Δ=16-8a(a+1)≤0，所以a≤-2.

评注本题根据函数的单调性去掉绝对值，然后移项，把相同变量放在同一边，使式子两边的结构相同，便于构造函数，利用同构变换巧妙解题.

五、通过巧妙放缩实施同构变换

所谓放缩有方，就是通过一些重要不等式进行巧妙放缩，使式子的局部的结构相同，然后再实施同构变换，使问题求解变得非常巧妙、简单.常用的不等式有ex≥x+1，ln(x+1)≤x等.

例6已知不等式对x ＞1 恒成立，求实数a的取值范围.

解因为x ＞1，所以lnx ＞0，所以因为ex≥x+1，即ex -x-1 ≥0，所以ex-3lnx -(x-3 lnx)-1 ≥0，所以等号成立的条件是x-3 lnx=0，即的最小值为-3，所以a≤-3.

评注本题就是先通过重要不等式ex≥x+1 进行放缩，使式子的局部结构相同，利用同构变换巧妙求解.这类放缩灵活性比较强，但解题过程非常简单，可谓“秒杀”，令人拍手称快.

六、使式子两边符合xex 型结构

观察式子的结构特征，通过巧妙的配凑，使式子两边的结构符合xex型结构，然后再构造函数f(x)=xex，利用函数的性质使问题巧妙求解.

例7已知函数f(x)=ex-aln(ax-a)+a(a ＞0)，若关于x的不等式f(x)＞0 恒成立，则实数a的取值范围为( )

A.[0,e2] B.(0,e2) C.[1,e2] D.(1,e2)

解由题设知ex ＞a[ln(ax - a)-1].因为a ＞0，ax-a ＞0，所以x ＞1，两边同乘x-1，得(x-1)ex ＞a(x-1)[lna(x-1)-1]=[lna(x-1)-1]elna(x-1).

令φ(x)=(x-1)ex，原不等式化为φ(x)＞φ(lna(x-1))，φ′(x)=xex ＞0，易知φ(x) 在(0,+∞) 上单调递增.若lna(x-1)=ln(ax-a) ≤0，则显然f(x)＞0 恒成立，若lna(x-1)=ln(ax-a)＞0，则x ＞lna(x-1)恒成立，即x ＞lna+ln(x-1)对x ＞1 恒成立，令h(x)=x-ln(x-1)，所以h(x) 在(1,2)上单调递减，在(2,+∞)上单调递增，lna ＜h(x)mⅰn=h(2)=2，所以a ＜e2，又a ＞0，所以0＜a ＜e2，故选B.

评注本题通过两边同乘x-1，使式子的两边结构相同，再构造函数，这种构造十分巧妙，需要有敏锐的观察力以及对同构变换技巧的掌握达到一定的熟练程度.

七、使式子两边符合型结构

观察式子的结构特征，通过巧妙的配凑，使式子两边的结构符合型结构，然后再构造函数利用函数的性质使问题巧妙求解.

例8已知0＜a ＜b ＜1，比较a·eb与b·ea的大小.

解要比较a·eb与b·ea大小，即比较大小，令f(x)=则f′(x)=所以f(x)在区间(0,1)是单调递减，因为0＜a ＜b ＜1，所以f(a)＞f(b)，所以所以a·eb ＜b·ea.

评注本题通过对两个数同除以ab，使式子的两边结构相同，再构造函数，使问题巧妙求解.

八、使式子两边符合x ln x 型结构

观察式子的结构特征，通过巧妙的配凑，使式子两边的结构符合xlnx结构型，然后再构造函数f(x)=xlnx，利用函数的性质使问题巧妙求解.

例9若对任意x≥1，恒有a(eax-1)＞2(x-)·lnx(a ＞0)，则实数a的取值范围是( )

A.(0,+∞) B.(,+∞) C.(,+∞) D.(0,)

解由a(eax -1)＞2(x-)·lnx，得a(eax -1)＞即(eax -1)·ln eax ＞(x2-1)·lnx2，令g(x)=(x-1)lnx，则g(eax)＞g(x2)，g′(x)=所以g′(x) 在(0,+∞) 上单调递增，又g′(1)=0，所以g(x) 在(0,1) 上单调递减，在(1,+∞)上单调递增，于是当x≥1 时，g(eax)＞g(x2)，eax ＞x2，ax ＞2 lnx，a ＞恒成立，令h(x)=(x≥1)，h′(x)=，由h′(x)＞0 得1 ≤x ＜e，由h′(x)＜0得x ＞e，所以h(x)在(1,e)上单调递增，(e,+∞)上单调递减，所以h(x)max=h(e)=所以故选C.

评注将已知不等式化为(eax-1)·ln eax ＞(x2-1)·lnx2，通过观察结构特征，根据同构变换的策略，构造函数g(x)=(x-1)lnx，把问题又划归到不等式g(eax)＞g(x2)，再利用函数g(x)的单调性，把不等式进一步划归到简单不等式eax ＞x2，这种变形虽运算量不大，但技巧性却非常强.

九、使式子两边符合x+ln x 型结构

观察式子的结构特征，通过巧妙的配凑，使式子两边的结构符合x+lnx结构型，然后再构造函数f(x)=x+lnx，利用函数的性质使问题巧妙求解.

例10已知实数α,β满足αeα=e3，β(lnβ -1)=e4，其中e 是自然对数的底数，则αβ=____

解法1对所给的两个式子两边分别取对数，则有α+lnα=3，lnβ-1+ln(lnβ-1)=3，令f(x)=x+lnx，f(α)=3，f(lnβ -1)=3，f(α)=f(lnβ -1)，易 知f(x)=x+lnx在(0,+∞)上单调递增，所以α=lnβ-1，lnβ-1+lnα=3，ln(αβ)=4，αβ=e4.

解法2由β(lnβ -1)=e4得，=e3=αeα=eαln eα，令f(x)=xlnx，=f(eα)，易 知f(x) 在(1,+∞) 上单调递增，易知，eα ＞1，所以=αeα=e3，所以αβ=e4.

评注(1)解法一通过巧妙配凑，使式子两边符合x+lnx结构型，然后再构造函数f(x)=x+lnx，利用函数的性质使问题巧妙求解.

(2)解法二通过巧妙配凑，使式子两边符合xlnx结构型，然后再构造函数f(x)=xlnx，利用函数的性质使问题巧妙求解.

十、使式子两边符合型结构

观察式子的结构特征，通过巧妙的配凑，使式子两边的结构符合结构型，然后再构造函数，利用函数的性质使问题巧妙求解.

例11对任意x ＞0，求证:x2＜(ex-1)ln(x+1).

证明即证即 证令f(x)=易知函数f(x) 在(0,+∞) 上单调递减，又易知x ＞0 时，x ＜ex -1，所以f(x)＞f(ex-1)，即命题得证.

同构变换为我们解题带来了新思路、新视野，其解法灵活、巧妙、简捷、新颖，给人带来美的享受和震撼，也使人们的思维在更广阔的空间得到发展，对培养人们积极思考、善于观察、勇于创新、追求简单的探究精神大有裨益.