过抛物线外任意一点作切线的方法
四川成都七中(610041) 杨 力 康 盛
在文章[1]中,给出了过圆锥曲线上任意一点作切线的方法.本文从中受到启发,先证明切线与过抛物线顶点且垂直于对称轴的直线的交点有一特殊性质,然后利用这一性质,给出过抛物线外任意一点作切线的方法,并予以证明.
一、先证明一个与抛物线有关的命题
命题1过抛物线y2=2px外一点P(x0,y0),作抛物线的切线l,l与y轴相交于点M,则过M且与l垂直的直线必过抛物线的焦点.
证明先求过点P的切线方程.如图1,设切点T(x1,y1),方程y2=2px(p >0) 两边对x求导,2yy′=2p,即:y′=所以由导数的几何意义得,过点T的切线的斜率所以过点T的切线方程为:

图1
再求切线与y轴的交点坐标.当x=0 时,
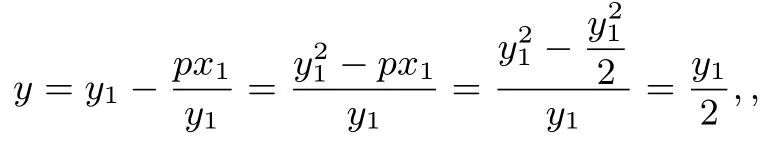
故点M的坐标为所以过M且与l垂直的直线方程为:(x-0),当y=0,x=则与x轴的交点为命题得证.
二、过抛物线外任意一点作切线的方法
已知切线上一点P,若再能确定一点即可作出切线.由命题1 可知,切线与y轴的交点,点P,抛物线的焦点,三点构成一个直角三角形.利用这个直角三角形,就可作出切线.
设P为抛物线外任意一点,F为其焦点,则过点P且与抛物线相切的直线作法如下:
第一步: 作以PF为直径的圆,与过抛物线顶点且与其对称轴垂直的直线分别交于M与N两点.
第二步: 连接PM,PN,则直线PM,PN就是过点P且与抛物线相切的直线.
证明如图2,以抛物线的顶点O为原点,其对称轴为x轴,建立平面直角坐标系.设抛物线方程为y2=2px(p >0),点P(x0,y0).以PF为直径的圆交y轴于点M,则有FM⊥PM,由命题1 可知,点M必在过点P且与抛物线相切的直线,则PM为抛物线的切线.同理可知,PN也为抛物线的切线.
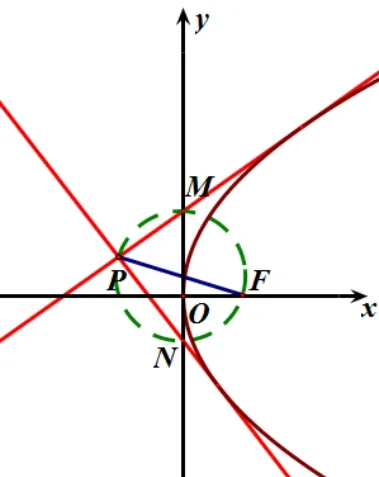
图2
本文提供了一种解决过抛物线外任意一点作切线问题的方法.但这种方法还需要抛物线的焦点位置,能不能找到一种不需要焦点参与的作法? 过椭圆与双曲线外一点,如何作切线呢?

