基于分数阶傅里叶变换和RVM的运动想象脑电信号分类方法

詹 宏 锋

(广东科学技术职业学院 广东 广州 510640)

0 引 言

脑-机接口(Brain Computer Interface, BCI)技术不依赖于传统的大脑外周肌肉和神经系统等输出通路，而是直接利用计算机等外围设备对脑电信号(Electro Encephalogram Gram, EEG)进行采集，进而运用模式识别方法对其进行分析并将特定任务下的EEG与不同的控制命令(例如敲击鼠标左键)建立联系，从而达到向外界输出信息的目的[1-4]。BCI技术中的关键是模式识别，即如何提取脑电信号中的有用信息(特征提取)并将这些信息与特定的控制命令联系起来(分类识别)。特征提取和分类识别作为模式识别中的难点，成为了当前研究的热点。特征提取是从高维的脑电信号中提取能够反映不同思维活动的差异信息，即实现从原始信号空间向低维特征空间的映射。分类识别是通过构建合适的分类器及选择最优的分类器参数对特征提取阶段获得的特征向量进行有效的区分，需要在保证分类性能和计算效率的前提下具备鲁棒性。

在特征提取方面，当前的研究主要集中在从脑电信号的时域、频域、空间域等变换域提取特征，例如快速傅里叶变换法(Fast Fourier Transformation, FFT)[5]、短时傅里叶变换法(Short Time Fourier Transformation, STFT)[6]、独立分量分析法[7]、小波变换法[8-10]等。FFT方法将脑电信号转换到频域，虽然能够提取频域中的信息，但是以损失时域信息为代价，不适于分析非线性、非平稳的EEG信号。STFT方法虽然能够对EEG信号的局部特征进行分析，但其时间分辨率和频率分辨率是相互矛盾的，即不能在得到高时间分辨率的同时保持高的频率分辨率，因此在对EEG信号进行分析时存在一定的局限性。CSP方法作为一种多通道分析方法，可以获得较好的分类结果，但是多通道的数据获取不仅增加了系统的复杂度而且降低了计算效率，限制了其在实际工程中的应用。小波变换能够对信号进行多尺度的细化分析，在面对非线性、非平稳的EEG信号时具备独特优势，因此被广泛应用于运动脑电信号分类。对信号进行小波分析时需要事先设置“基函数”，文献[11]分析表明“基函数”的选取对分类性能存在较大影响，而如何选择合适的“基函数”当前还没有很好的办法。

上述分析表明，现有方法虽然能够提取出反映不同运动脑电信号中包含的差异特征，但是由于这些方法仅仅是从某个特定的变换域对运动脑电信号进行分析，提取的特征较为单一，没能包含不同维度的信息，具有一定的局限性，同时在小样本条件下或信噪比较低时，也会存在分类识别性能下降的问题。

针对上述问题，本文提出将分数阶傅里叶变换理论应用到运动脑电信号的特征提取中，将现有特征提取方法扩展到分数域，利用不同阶次的FRFT对信号进行分析，从中提取数量更多、包含信息更完善的分数阶特征，在此基础上利用相关向量机对特征选择和分类函数进行联合优化，剔除冗余特征并得到最优的特征组合。基于实测数据的实验结果表明，本文方法相对于传统方法具有更好的可分性和更高的识别性能，并且在小样本和低信噪比情况下具有更强的鲁棒性。

1 分数阶傅里叶变换

傅里叶变换自1807年由Fourier提出以来，在理论研究和工程实践方面都发挥了极其重要的作用，也是当前应用最为广泛的一种数学工具。但是随着对信息科学理论研究的深入，FFT的局限性也逐渐暴露，由于FFT是一种全局变换，只能将信号由时域整体转换至频域，频谱上的任何一点都是由整个时间域内信号的贡献决定，无法对信号的局部变化情况进行分析，在面对非线性、非平稳信号分析需求时应用受限的问题愈发突出。在这种情况下，国内外学者开展了大量研究并提出了一系列针对非线性、非平稳信号进行分析的新方法，如小波变换、短时傅里叶变换、Gabor变换、FRFT等，其中FRFT作为一种广义的傅里叶变换，在保留传统FFT特点的基础上增加了其特有的优势，具备对信号的时域和频域双域的信息融合处理能力，逐渐发展成为一种分析非线性、非平稳信号的强有力工具[12-15]。

图1 FRFT与FFT关系示意图

对于任意连续时域信号f(t)，经p阶FRFT后得到的分数域信号fp(u)可以表示为：

(1)

式(1)给出的是连续信号的FRFT，而实际数字信号处理工程应用中都是针对离散信号进行处理，需要使用离散形式的FRFT，即离散分数阶傅里叶变换(Discrete Fractional Fourier Transform, DFRFT)。当前常用的计算DFRFT的方法主要包括三种：1) 利用DFT核矩阵的特征值和特征向量构造DFT核矩阵的分数幂来计算DFRFT；2) 根据FRFT的定义，将其分解为一个chirp信号与调制信号卷积的形式，然后利用FFT计算得到DFRFT；3) 通过某些特点阶数的DFRFT的线性组合计算得到任意阶数的DFRFT。其中第2种方法由于精度和效率较高，目前应用最为广泛。式(1)可以按如下方式进行展开：

exp[-j2πutcscα]dt

(2)

根据Shannon定理[12]，函数f(t)exp[jπt2cotα]可以表示为：

(3)

将式(3)代入式(2)即可以得到信号f(t)的离散分数阶傅里叶变换fp(m)为：

(4)

2 实验数据

实验采用文献[4]中选用的BCI 2003年国际竞赛所用Dataset Ⅲ标准数据集。实验过程中要求受试者按照提示通过想象左右手运动实现对光标移动的控制。每次实验持续时间为9 s，图2为每次实验的时序：

1) 0≤T<2 s，准备时间，受试者处于平稳放松状态；

2)T=2 s，开始提示，屏幕上出现十字光标示意受试者实验即将开始；

3) 3≤T<9 s，实验时间，受试者根据屏幕出现的向左或向右的箭头对应想象左手或者右手运动。

图2 实验数据采集时序

实验过程中采用差分电极，实验数据从国际标准的10～20导联系统的C3和C4两个通道获取。数据集中总共包含280组实验数据，其中140组为训练数据(包含70组想象左手运动数据和70组想象右手运动数据)，剩余140组为测试数据(包含70组想象左手运动数据和70组想象右手运动数据)。实验中采样频率设置为128 Hz，每次实验包含1 152个采样点，根据图2所示实验时序，由于每次实验是从第3 s开始，因此为了提升计算效率，本文对每组实验数据选用第3～9 s的数据共768个采样点。

3 基于FRFT的特征提取

对于任意给定的一组信号，分别对其进行p阶离散分数阶傅里叶变换p=0,0.1,…,1，可以得到对应的分数域信号fp(m)，m=1,2,…,M，M为采样点数。当p=0时得到的f0(m)为原始时域信号；p=1时得到的f1(m)为原始信号对应的频谱。

图3(a)和(b)分别给出了对想象左手运动和想象右手运动的C3通道实测数据进行不同阶次FRFT得到的分解结果，可以看出随着阶次的增加，信号的时域特性逐渐减少，频域特性逐渐增加，即不同阶次的分解结果呈现了信号由时域过渡到频域的完成过程。同时对比图3(a)和(b)可以看出，想象右手运动脑电信号和想象左右运动脑电信号存在一定差异，想象右手运动脑电信号支撑区宽度明显大于想象左右运动脑电信号。图4(a)和(b)分别给出了C4通道实测数据的分解结果。从图3和图4可以看出，相同运动方式的C3和C4通道信号的FRFT分解结果具有一致性。每幅图的横坐标为采样点，纵坐标为归一化幅度。

(a) 想象左手运动

(b) 想象右手运动图3 C3通道不同阶次FRFT

(a) 想象左手运动

(b) 想象右手运动图4 C4通道不同阶次FRFT

针对运动脑电信号分类问题，当前的特征提取方法大都是采用时域、频域或小波域等变换域的特征，虽然能够获得较好的分类结果，但都是从某一特定变换域中进行分析，特征提取维度少，特征中包含的信息量不足，并且对测试数据信噪比要求较高，在信噪比较低的条件下分类性能会有明显下降。针对上述问题，本文在对信号进行FRFT的基础上，将特征提取维度扩展到分数域，从而提取更多特征，扩充特征中的有用信息。

1) 分数阶信号的二阶中心距特征：

(5)

2) 分数阶信号的方差特征：

(6)

方差特征反映的是信号的波动特性。

3) 分数阶信号的熵特征：

(7)

4) 分数阶信号的支撑区宽度特征：

(8)

式中：find(·)为寻找满足条件的样本点总个数的函数。

对0～1阶分数阶信号分别提取上述四维特征，可以得到由44维特征构成的特征向量如表1所示。

表1 分数域特征

4 特征选择及分类

得到特征向量后，需要设计合适的分类算法才能得到期望的分类性能，虽然分数域的特征提取方法实现了特征域的扩展，但是提取的44维特征中不可避免会存在一些冗余特征，这些特征的存在不仅不会增加对分类有用的信息，相反可能会降低分类性能，因此在分类识别前需要采用特征选择方法将其剔除。

目前常用的特征选择方法为序列浮动前向选择法(Sequential Forward Floating Selection method,SFFS)[16]，该方法需要预先设定期望的特征个数d，实验过程中每次从特征总集合中选入或者抽掉某一些特征，直至得到包含d个特征的最优分类结果。这种方法通过遍历的方式找到最优的d个特征向量，但是预设特征个数d的确定存在困难，并且算法需要消耗较大的运算资源。

相关向量机由Tipping等[16]基于贝叶斯框架提出，与SVM类似，RVM也是通过核函数将低维空间的线性不可分问题转换为高维空间的线性可分问题，同时又具备独特的优势：1) RVM模型具备更高的稀疏性，因而能够自动实现特征选择； 2) RVM模型设计中充分实现了对分类器设计和特征选择的联合优化，保证了两者具备相同的优化准则； 3) 核函数的选择不受摩西准则约束； 4) RVM能够提供概率式的预测分布。

运动脑电信号分类作为典型的两类分类问题，对于给定的训练样本集{xn,tn}，n=1,2,…,N，N为训练样本个数，tn∈{0,1}为类别标号。两类RVM分类函数为：

(9)

式中:K(x,xn)为核函数;wn代表不同的权重;ε为均值为0，方差为τ-1的高斯分布。为了对输入向量对应的目标值作出概率预测，将Sigmoid函数引入分类函数，此时样本集的似然函数可以表示为：

(10)

为了构建完成的贝叶斯模型，假设wn的先验分布为均值为0，方差为α-1的高斯分布。由于高斯分布的共轭先验分布为伽马分布，因此用伽马分布定义α-1和噪声方差τ-1的超先验：

(11)

p(τ)=Gamma(τ|c,d)

利用VBEM算法对参数后验分布的求取过程中，大部分α会随着迭代过程趋于无穷大，对应的w则趋于0，从而实现了权值向量的稀疏化，此时不为0的权值对应的特征向量即为要选择的特征。

5 实 验

首先选取数据集中的140组数据作为训练样本，其中包含想象右手运动数据和想象左手运动数据各70组，剩余140组作为测试数据，将本文方法和近年来其他文献中介绍的方法进行对比，结果如表2所示。其中：文献[17]采用小波包能量特征并利用基于马氏距离的线性分离器；文献[18]采用小波熵特征并利用SVM分类器对运动脑电新年好进行分类；文献[19]在文献[17]的基础上利用Burg算法提取脑电信号的5阶AR模型稀疏作为特征并利用线性分类器获得了93.43%的分类结果。可以看出，本文提出的分数域特征结合RVM分类器的运动脑电信号分类方法可以获得最好的分类性能。

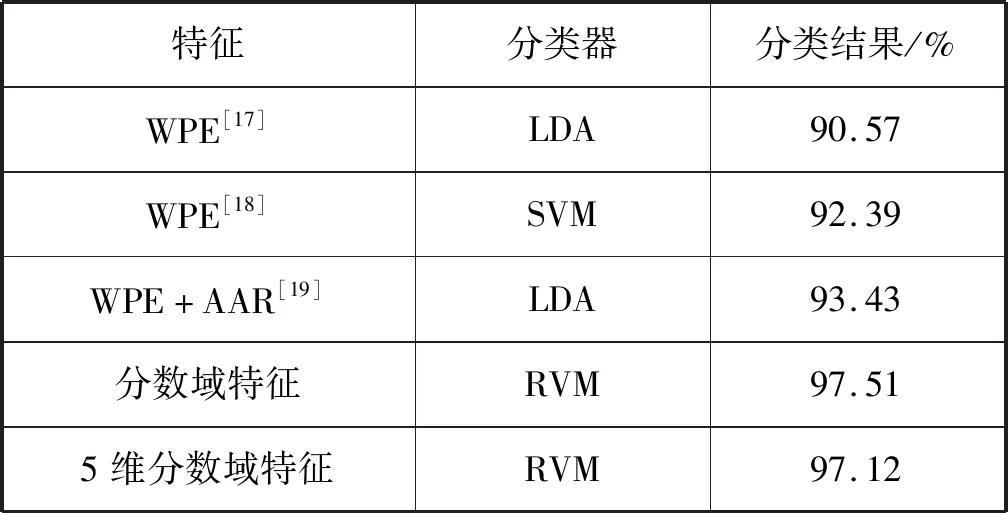
表2 不同方法的分类结果

图5为利用RVM分类器对44维分数域特征进行特征选择的结果，可以看出经过特征选择后，对应权值较大的特征有5维：Feature20.9，Feature30，Feature30.7，Feature40.8，Feature41，既包含了传统的时域特征和频域特征，又包含了不同阶次的分数域特征，体现了信息提取维度和特征的多元化。表2中最后一行给出了只采用上述5维特征并利用RVM分类器进行分类可以得到97.12%的正确识别率，该结果表明44维分数域特征中，该5维特征对分类结果的贡献要远远超越其他39维，说明RVM特征选择的准确性和有效性。

图5 RVM分类器特征选择结果

图6为上述5维特征的二维归一化特征分布图。可以看出RVM选择出的5维特征在特征域存在明显的差异，具备较好的可分性。

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

(j)图6 RVM选出的5维特征的二维特征分布图

对于运动脑电信号分类问题，除了正确分类性能外，小样本条件下的泛化能力和低信噪比条件下的噪声稳健性在实际工程应用中同样具有重要意义。

实验过程中通过减少训练样本、增加测试样本的方式验证本文方法在小样本条件下的泛化能力(总数据集不变)。图7给出了训练样本数变化时不同方法的分类性能，可以看出本文方法在训练样本减少至60组时，依然能够获得95%以上的分类性能，体现出了强泛化能力。同时文献[18]采用的WPE+SVM的方法在样本减少时也表现出了较强的鲁棒性，这是由于RVM与SVM采用一致的分类函数，都具备在小样本条件下强推广能力，而LDA分类器不具备该能力，分类性能随着样本的减少逐渐变差。

图7 分类性能随训练样本数的变化曲线

脑电信号的幅度通常处于μV级，微弱性特征明显，容易受到噪声污染，因此要求分类方法具备低信噪比条件下的噪声稳健性。为了验证本文方法在不同信噪比条件下的分类性能，实验过程中采用在实验数据中加入高斯白噪声的方式进行分析。本文中信噪比(SNR)定义如下：

(12)

图8给出了不同信噪比条件下的分类性能。可以看出，本文方法在低信噪比条件下相对于其他方法可以获得更好的分类性能，SNR优于15 dB时仍然可以获得85%以上的正确分类结果，相对于其他方法具备更好的噪声稳健性。

6 结 语

对非线性、非平稳脑电信号的特征提取和分类识别是当前脑机接口技术研究的热点。本文提出一种基于FRFT和RVM的运动想象脑电信号分类方法，首先利用FRFT将信号从时域转换至分数域，充分扩展了特征提取维度，然后利用RVM分类器对分数域特征进行选择，剔除冗余特征从而降低运算复杂度。基于实测数据的实验结果表明相对于其他现有方法，本文方法可以获得更好的分类性能。同时本文通过设计合理的实验对所提方法在小样本情况下的返还能力和低信噪比条件下的噪声稳健性进行了验证，实验表明本文方法在样本数减少至30%时仍然可以获得90%以上的正确分类性能，在信噪比优于15 dB时可以获得85%以上的分类结果，均优于其他对比方法。