基于博弈视角和实物期权理论的养老机构PPP 项目运营补贴机制研究

吴 凡，曾颖妍

（华南理工大学 土木与交通学院，广东 广州 510641，E-mail：zengyingyan@foxmail.com）

步入 21世纪以来，我国人口老龄化的形势越显严峻，同时我国家庭结构不断往小型化发展，居家养老模式不仅逐渐加重家庭负担，也与老年人不断增长的对高品质生活的追求产生越来越多的矛盾。而社区养老规模有限，且服务质量、完备程度和及时性难以得到保证，因此机构养老的支撑作用显得越来越重要[1]。而与此同时，我国养老服务机构床位供给缺口巨大，供需矛盾十分突出。在此背景下，机构养老服务项目结合政府和社会资本合作（Public-Private Partnership，PPP）模式成为一个可行的解决方案。虽然养老服务产业属于公共服务领域，但养老机构及其服务又具有准经营性，因此适度引入市场竞争机制有利于提高养老服务产业的供给效率[2]。然而PPP模式在近几年的快速发展后进入反思阶段，由于各参与方沟通和协商不充分，投资决策不科学，易导致项目流产、落地困难等风险，为项目后续的运营埋下隐患，同时也容易使地方政府增加巨额隐性债务。在此背景下，对养老机构PPP项目进行合理的制度模式设计，能在逐步收紧的PPP政策下开辟一条可持续的发展道路，通过利益共享、风险共担，提高项目运营效率，对推进养老机构PPP项目的风险管控和规范化，促进养老产业和PPP模式的健康协同发展有着重大意义。

针对PPP模式，国内外研究都较为成熟。Jui-Sheng Chou等[3]总结了案例国家和地区的基础设施采购PPP项目关键成功因素，以及偏好的风险分配策略。Robert Osei-Kyei等[4]通过加纳和中国的对比分析，评估PPP项目矛盾的根源，并寻求合适的矛盾化解机制。在PPP项目特许期决策方面，传统的现金流折现（Discounted Cashflow Model，DCF）方法应用最为广泛。李启明等[5]在传统净现值法的基础上提出了项目特许期的数量决策模型。传统DCF方法虽然操作简单，但其依赖于对未来现金流预测的准确性，且将不确定性全部视为风险，忽略了不确定性带来的项目潜在价值，因此不适合处理不确定性环境下的投资决策问题[6]。基于此，国内外学者将博弈论和实物期权理论应用于PPP项目的特许期决策，弥补了DCF模型的不足。Ke Feng等[7]基于讨价还价博弈，计算一系列假设下的PPP项目最佳特许权期限，并分析不同因素对最优特许期的影响。Guofeng Ma等[8]和史翔等[9]将实物期权价值的分配纳入决策过程，结合博弈论计算PPP项目特许期。冯永洲[10]利用蒙特卡罗模拟将实物期权价值定量化，构建基于实物期权的PPP项目特许权期决策模型。

在PPP模式下，为降低社会投资者的经营负担，政府一般会对私人部门进行补贴。Chowdhury等[11]认为政府对私人投资者的补贴对PPP项目融资起着关键作用。在补贴机制设计方面，王卓甫等[12]建立政府方与私人方的Stackelberg博弈模型，求解公益性PPP项目的最优特许期限及政府支付给私人方的最优年补贴成本。朱保霞等[13]基于讨价还价博弈模型设计了政府、项目公司和管线单位三方共赢的灵活补贴机制。现阶段我国对于养老类PPP项目的运作模式设计仍在尝试与摸索中。孙玉栋等[14]认为要通过合理的责任分摊缓解政府的财政压力并保证社会资本适当获利。杨凯峰[15]对PPP模式下的养老机构进行定价机制研究，构建“三方合理”养老产业PPP项目定价模型。

综上，目前PPP项目定价和特许期决策模型的研究对象多为大型公共项目，如污水处理、收费公路等，以养老机构PPP项目为对象，充分考虑其项目特征的研究较少。在PPP模式与养老机构项目结合的研究上，多数停留在理论层面和定性研究，相关定量模型的建立以及实证计算检验较少，且运用的研究方法较为传统。在已有研究的基础上，本文将基于博弈视角和实物期权理论对养老机构PPP项目进行运营补贴机制设计以及定量化测算。

1 基于讨价还价博弈的项目补贴博弈模型

在养老机构PPP项目的开发运营过程中，政府希望通过引入社会资本减轻财政负担，提高项目的社会效益；而私人投资者则希望通过参与项目获得合理的利润回报。二者之间行为相互作用，寻求利益均衡，具有显著的博弈特征，可运用博弈论来分析养老机构PPP项目补贴分配的问题。

1.1 补贴模型前提假设

（1）床位费与其他配套服务费是养老机构PPP项目公司的主要收入来源，且经营收入不足以弥补建设成本和运营成本。根据企业和政府签订的合同，约定公益性床位和经营性床位比例及收费价格，由于养老机构运营专业性强，成本较高，单凭使用者付费很难实现盈利，需要政府对项目公司进行可行性缺口补助。

（2）政府在运营阶段对项目公司进行补贴。养老机构PPP项目的特许期可划分为建设期和运营期，政府对PPP项目的补贴以运营阶段补贴为主。将运营补贴分为固定补贴和可变补贴，固定补贴用于保证项目可持续运营，可变补贴则与项目公司运营绩效挂钩，起到监督和激励的作用。

1.2 贴现率与补贴金额的确定

投资回报率（Return on Investment，ROI）指企业从一项投资活动中得到的经济回报，涵盖了企业的获利目标。学者常常与其测算方法相结合，将投资回报率等同于“贴现率”[13]。秦旋[16]指出私人投资者对项目的投资包括股本资金和债务资金，在确定贴现率时应考虑股本资金的机会成本以及应该获得的合理的风险报酬，因此私人投资者应采用风险校正贴现率作为财务测算指标。对于养老机构PPP项目公司，资金投入由股本资金和债务资金两部分组成，使用加权平均资金成本作为项目的贴现率，则风险校正贴现率radj为：

式中，rc表示股本资金成本；rd表示债务资金成本，可取项目特许期贷款利率；c表示项目股本资金的市场价值；d表示项目债务资金的市场价值；γ表示项目公司税率。

根据式（1）计算得到合理的投资回报率，设项目特许期为t，包括建设期t0和运营期t1，则养老机构 PPP项目在运营阶段的净现值（Net Present Value，NPV）为：

式中，Ci表示建设阶段项目公司第i年的建设成本；Si表示运营阶段第i年政府支付给项目公司的补贴额；Ii表示运营阶段第 i年项目公司的营业收入；Mi表示运营阶段第i年项目公司的运营成本。

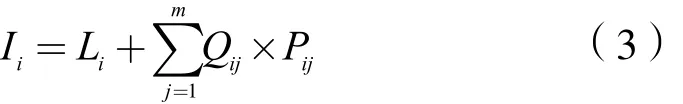
式中，Li为第i年的配套服务收入；设养老机构共有m种床位，Qij表示第i年第j种床位的入住量；Pij表示第i年第j种床位的收费价格。

在我国，PPP项目政府补贴一般以每年均等数额给予项目公司，补贴金额的确定要从政府和投资者双方的角度加以考虑。从私人投资者的角度来看，项目必须具备可行性和可持续性，因此补贴金额的下限 Smin为令项目净现值 NPV=0时的补贴金额：

从政府的角度来看，当投资一个项目获得的收益使项目净现值达到预期的资金回报时，社会投资者才愿意参与。但由于养老机构PPP项目具有非营利性，因此要控制项目收益率，确定补贴金额上限时不以总投资额来测算收益，只考虑股本资金的合理回报，即项目补贴金额的上限Smax为令项目净现值时的补贴金额，则：

式中，Ic为项目资本金；RC为项目资本金回报率；等额年金现值系数

为利用政府补贴形成激励机制，将政府补贴分为固定补贴和可变补贴两部分，固定补贴S1保障项目公司正常运营，Smin≤S1＜Smax。可变补贴 S2用于激励项目公司提高运营效率与服务质量，S2=φ×系数φ与项目绩效考核评价有关。称K为可变补贴比例，则固定补贴S1=(1-K)Smax。由此形成固定补贴和可变补贴相结合的养老机构PPP项目补贴激励机制。

1.3 基于讨价还价博弈模型的补贴比例计算

可变补贴作为项目不确定因素，风险由私人投资者承担，因此政府希望可变补贴比例越大越好，与之相反，私人投资者则希望可变补贴比例越小越好。为寻求利益均衡，可变补贴比例K可通过讨价还价博弈模型确定。提出以下假设：

（1）博弈双方政府部门（G）和社会投资者（P）均为理性人。

（2）第一回合由政府部门先出价，提出可变补贴比例K1，私人投资者可选择接受或拒绝，若接受则博弈结束，若拒绝则进入下一回合，由私人投资者出价K2，以此类推。每一回合双方交替出价，提出的可变补贴比例为Kn，n=1，2，…，n。

（3）考虑谈判成本，每进行一回合双方利益均有损失，设政府损耗系数为δg，0<δg<1；私人投资者损耗系数为 δp，0<δp<1；且 δg>δp。

鲁宾斯坦（Rubinstein）模型中把讨价还价过程视为合作博弈的过程，根据该模型，双方在经过无限回合博弈后，模型的纳什均衡解即固定、可变补贴的比例为在实际情况中，由于损耗系数的存在，参与人在下期所得份额X经过贴现后只等于本期的 δX，且项目的谈判时间有一定限制，因此博弈双方都希望尽快接受对方合理报价以减少利益损耗。

为控制利益损耗和谈判时间，本文假设博弈最多进行3个回合，在第三回合中政府提出可变补贴比例K3，无论私人投资者是否接受，第三回合后博弈都将结束。设可行分配集 K={(Kn，1-Kn)|0≤Kn≤1，n=1，2，3}；在第 n回合，政府方得益私人投资者得益若第三回合私人投资者拒绝政府的出价，则谈判破裂，项目流产，双方得益均为零。政府和私人投资者双方的博弈过程可用扩展式表示，如图1所示。

可利用逆推法求解上述博弈模型的解。在第三回合，由于谈判破裂双方得益均为零，因此只要使私人投资者得到的固定补贴大于等于补贴金额下限 Smin，私人投资者必定会接受，令 P3=Smin，即：

图1 政府和私人资本方讨价还价博弈模型扩展式

对于政府而言，第三回合的K3等价于第二回合时的 δgK3，因此若企业在第二回合时提出的K2=δgK3，则政府必定接受。在第二回合，企业的1-K2=1-δgK3等价于第一回合时的 1-K1=δp-δpδgK3，即 K1=1-δp-δpδgK3，因此若政府在第一回合提出K1=1-δp-δpδgK3，企业必定接受。

因此可得三回合讨价还价模型的解，即可变补贴的比例为：

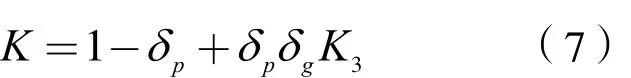
将式（6）代入式（7），可得：

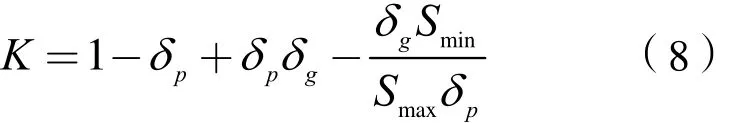
式（8）即为养老机构 PPP项目可变补贴比例的计算公式。

2 基于实物期权的项目特许期计算模型

项目的可变补贴受实际运营情况影响较大，具有不确定性。基于传统NPV法计算项目特许期时，若只考虑固定补贴，不将可变补贴纳入测算体系，则忽略了不确定性带来的项目潜在价值；若计算最高可能补贴，不考虑实际情况下可变补贴的波动性，则忽略了隐藏的风险，会导致投资者无法获得预期回报。因此本文引入实物期权理论建立项目特许期计算模型，使模型充分考虑可变补贴带来的期权价值，更适应PPP项目的多变性。

实物期权（Real Options）理论把金融市场的规则引入企业内部战略投资决策，是管理者对所拥有实物资产进行决策时所具有的柔性投资策略。可变补贴可看作一种担保期权，当项目公司运营绩效考核分数达到政府考核标准时，项目公司可获得相应数额的可变补贴，此时可以认为项目公司实施了看涨的担保期权。可变补贴S2的考核系数φ与考核得分ω相关，即：

f(ω)由项目公司与政府协商制定。项目担保期权价值为：

式中，S2i表示运营期第i年项目公司获得的可变补贴；rf表示无风险利率。由于项目绩效考核评分具有不确定性，可通过对项目运营期内的各年考核成绩进行概率分布假设，利用蒙特卡罗模拟对不同年份的担保期权价值进行模拟计算。考虑担保期权后的项目总价值：

3 实证分析

YX市某城市综合养老院PPP项目，项目用地面积为49922.3 m2，建筑总面积为55232m2。项目采用 BOT（Build-Operate-Transfer）模式，初始特许经营期为30年，其中建设期为3年，项目静态投资25501万元，其中项目资本金为1亿元。资本方融资利率为5.39%，资本金回报率6%，通过式（1）计算得修正贴现率radj为5%。则有IC×RC×(P/A，i，n)=9223.47万元。

项目建成后设置1117张养老床位，其中政府供养老人床位不低于212张，自理老人床位234张，护理老人床位671张（包括失智老人床位36张），床位使用率和员工数目均逐年增长，到运营期第 6年趋于稳定。对项目中的收费标准与成本做出测算，得现金流量表如表1所示。

根据式（4）计算得投资者可接受的年总补贴额下限Smin为1935.78万元；根据式（5）计算得政府可接受的年补贴额上限Smax为2664.95万元。本项目政府损耗系数δg为0.95，私人企业损耗系数δp为0.9，根据式（8）计算得可变补贴比例K为0.188。因此项目年固定补贴S1=(1-K)×Smax=2163.25万元。

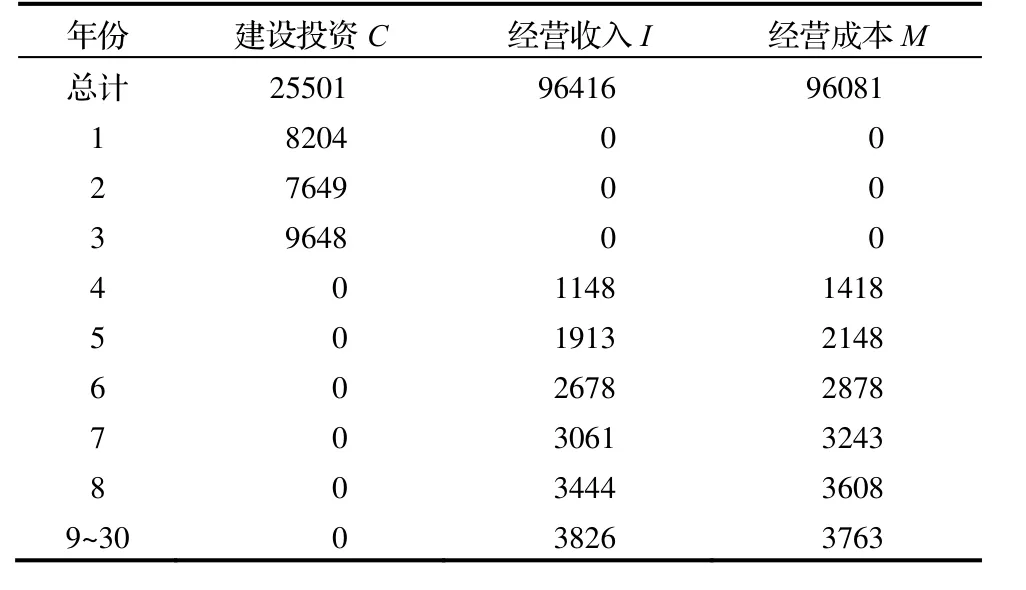
表1 Y X市养老院PPP项目现金流量表（单位：万元）

根据初始特许期确定补贴金额和分配方案后，项目的实际特许期应根据可变补贴带来的期权价值进行调整，运用蒙特卡罗模拟担保期权价值，作如下假设：

假设一：项目可变补贴金额与年度绩效考核结果挂钩。考核为百分制，考核系数φ计算式如下：

假设二：无风险利率rf取立项当年国债利率4.17%。

假设三：假定项目每年的考核分数波动符合正态分布（76.67，7.67），选取试算年份15~30年。

则项目累计净现值NPV1为仅计算固定补贴S1，不考虑可变补贴期权价值时的项目净现值：

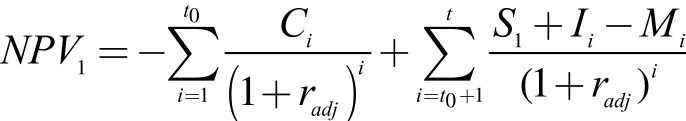
根据考核规则，当项目年绩效考核低于 60分时，当年项目公司不会获得可变补贴，当绩效考核在 60分以上时，按式（12）确定考核系数，结合式（9），则特许期第i年政府给予项目的可变补贴S2i为：

可变补贴的担保期权价值为：

项目的担保期权价值Vg可通过 CRYSTAL BALL11.1.2.4进行蒙特卡罗模拟计算（本文模拟次数为 10000次）。从而计算出基于担保期权价值的项目总价值V，结果如表2所示。

由表2可知，基于固定补贴的累计净现值NPV1在特许期第24年为566.56万元>0，因此24年为不考虑可变补贴潜在价值时的投资回收期，可作为特许期谈判的政府可接受上限tmax。考虑可变补贴担保期权价值后，项目总价值V在特许期第19年即可达到476.68万元>0，因此19年可作为特许期谈判的投资者可接受下限tmin。图2为对第19年时的担保期权价值的蒙特卡罗模拟结果。

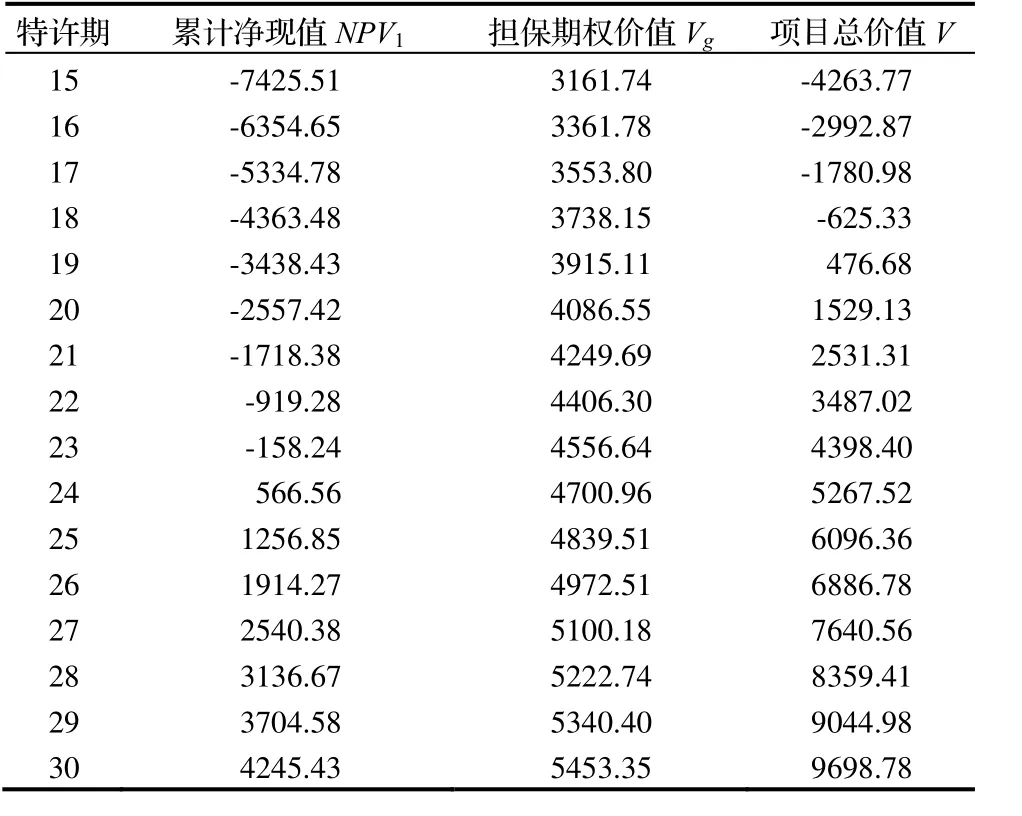
表2 基于担保期权的项目价值计算（单位：万元）

图2 第19年时担保期权价值的蒙特卡罗模拟结果图

综上，项目年固定补贴为2163.25万元，（19，24）为项目特许期谈判区间。具体谈判过程可参考有限讨价还价博弈模型，运用式（8）进行计算：

也可由社会投资者与政府考虑其他风险因素等详细条件再协商确定。

4 讨论

案例项目原特许期 30年，原补贴方案每年补贴金额固定，政府补贴静态总额为42321万元。应用本文构建的运营补贴机制和特许期决策模型后，项目年固定补贴S1为2163.25万元，特许期t为21年，此时政府支付的固定补贴静态总额为38938.44万元。与原方案相比较，本文设计的运营补贴机制在保障社会资本合理收益的同时，固定补贴总额比原方案补贴总额少3382.56万元，特许期缩短9年。在此基础上设置动态补贴不会对政府财政造成大的负担，同时与绩效考核挂钩的形式在很大程度上激励项目公司提高服务质量。而更短的特许期则使得政府在收回经营权时项目还保留有较高的固定资产余值，给予政府更大的经营空间。

从政府的角度来讲，可变补贴的设置不仅能降低政府的固定补贴支出，更重要的是能矫正私人投资者对政府补贴过度依赖而导致的运营效率低下，加强政府对项目的监控和引导作用；从私人投资者角度看，固定补贴满足了项目最低运营条件，而可变补贴具有超额收益的可能，增加了项目的潜在投资价值，具有一定投资吸引力，通过对期权价值的合理测算，也有更充裕的特许期谈判空间；从使用者（入住养老机构的老年人）角度来看，政府补贴保证了机构价格的稳定性和普惠性，而补贴激励机制调动了私人投资者运营积极性，使老年人享受低价高质的服务成为可能。本文建立的运营补贴机制和特许期决策模型具有其可行性与合理性，较好地发挥政府补贴的积极引导作用，在政府、社会投资者和使用者三方合理的基础上有效提高了项目社会效益。

5 结语

本文论证了养老机构和PPP模式相结合的可行性，对PPP项目利益分配问题有一定参考价值。基于讨价还价博弈，本文提出固定补贴和可变补贴相结合的机构养老PPP项目政府补贴激励机制，该机制实现了政府、社会投资者和使用者三方共赢，并且引入实物期权理论测算项目真实的投资价值，建立了考虑期权价值的项目特许期计算模型，弥补了传统贴现现金流分析方法的缺陷，为养老机构PPP项目的科学决策提供方法论的参考。但研究中还存在一些不足在今后可以继续深化：如考虑更多种情况的讨价还价博弈，构建普适性更强的博弈模型；对项目绩效考核成绩的概率分布假设可寻找更多数据支撑，尽可能降低模型主观性。科学合理的运营机制设计和投资决策是养老机构PPP项目可持续运营的基础，政府和私人投资者应吸取过往同类项目的经验，不断提高管理水平和决策能力，推动PPP模式和养老产业的有机结合，实现一加一大于二的协同发展。