基于NRS-BP模型的商品住宅需求预测研究

谷甜甜，李德智，杨 茜，蒋 英

（1.中国矿业大学 力学与土木工程学院，江苏 徐州 221116，E-mail：gusweet@126.com；2. 东南大学 土木工程学院，江苏 南京 211189；3.江苏城乡建设职业学院 管理工程学院，江苏 常州 213147）

当前我国城镇化进行的加速使得商品住宅需求旺盛，总体住房短缺问题仍存在[1,2]。因此识别住房需求的关键影响因素，构建合理的预测模型分析住宅需求未来走势，对于促进住房供给科学决策、住房建设合理投资、乃至形成平稳健康发展的房地产市场具有十分重要的意义。

在商品住宅需求及其预测的研究上，国内外许多学者进行了深入且积极的探索，发现国家、消费者、供给方等多方面因素对城镇商品住宅需求量产生综合影响，其预测方法也多种多样。其中，国家层面的影响因素主要包括GDP、国内生产总值增长率、城镇化率、房地产开发投资完成额[2~4]；消费者方面影响因素主要包括人均居民可支配收入、家庭规模、人均居住面积、居民消费价格指数等[5,6]；住宅市场的供给方主要是指房地产开发商，对于住宅需求的影响因素包括住宅平均价格、住宅竣工面积、新开工面积等[7,8]。考虑到影响商品住宅需求的因素较多且通常呈现非线性关系，传统的线性回归、主成分分析法（PCA）、德尔菲和层次分析法等无法从本质上反映真实问题。近年来部分学者在进行商品住房需求影响因素分析及未来趋势预测上，采用人工神经网络方法并取得了一定效果，例如葛怀志等[2]应用基于PCA-BP模型分析了湖北省城镇居民住房需求的9个影响因素，为住房需求的预测提供了一定的参考。

然而，国内外在住宅需求影响因素指标选取上往往缺乏科学根据，仅仅考虑少数几个和需求相关因素的面板数据。因此，本文从简单且切实可行角度出发，提出基于邻域粗糙集（Neighborhood Rough Set，NRS）和“误差反向传播”（Back Propagation，BP）神经网络的住宅需求预测模型，从住宅需求的众多影响因素中筛选出主要影响因素，利用BP神经网络方法，预测城镇居民住宅需求的未来走势，并选取某市A区作为算例分析。

1 基于NRS-BP的商品住宅需求预测模型

在粗糙集理论基础上，邻域粗糙集（NRS）作为约简方法被提出用于处理混合型属性值[9]，其广泛地应用在决策模型构建、评价指标体系构建、影响因素提取等方面[10]，然而 NRS无法对属性数据进行预测。BP神经网络作为人工智能的一种方法，用于对数据进行运算和规律识别，在人力资源需求、能源需求、建设用地需求等方面具有较好的预测能力[11,12]。本文基于NRS-BP构建商品住宅需求预测模型如图1所示。

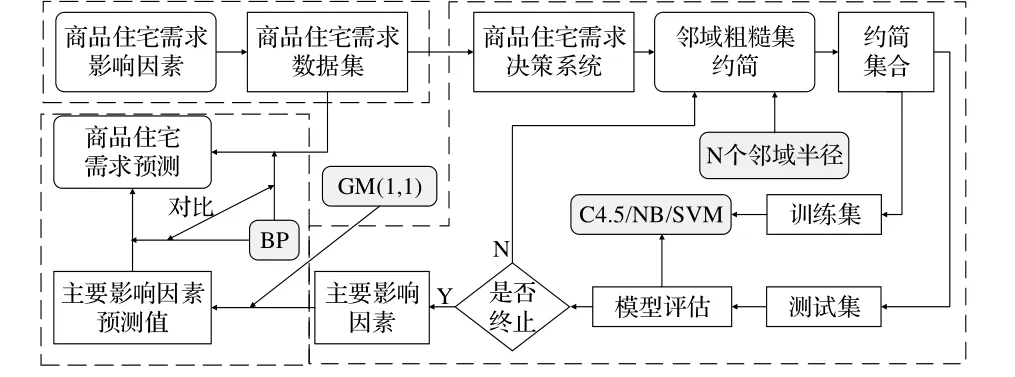
图1 基于NRS-BP的商品住宅需求预测流程

1.1 商品住房需求影响因素的确定

考虑到我国住宅需求中微观层面数据难以获取和政策层面因素难以度量两方面情况，从商品住宅需求数据的有效性及可得性出发，采用宏观经济时间序列数据来构建预测模型，选取城镇常住人口（a1）、住宅竣工面积（a2）、GDP（a3）、城镇化率（a4）、住宅投资额（a5）、家庭规模（a6）、主要年份城镇非私营单位职工年平均工资（a7）、人均居民可支配收入（a8）、人均居住面积（a9）、国内生产总值增长率（a10）、城镇居民恩格尔系数（a11）、商品住房均价（a12）、居民消费价格指数（a13）、住宅施工面积（a14）、住宅新开工面积（a15）等作为商品住宅需求的影响因素。商品住宅需求指的是某一时期消费者能够并有意愿购买的商品住宅产品，通常表征指标为商品住宅销售面积[13]，因此本文将商品住宅销售面积作为决策变量（D），并以时间为单位对某地区商品住宅需求量进行预测。

1.2 商品住房需求关键影响因素确定

利用需求数据集构建决策信息表，明确商品住宅需求决策系统。针对表述的需求影响因素约简问题，将其转化成一个决策系统。论域U={x1，x2，…，xn}是全部样本构成的集合，其中xi=(i=1，2，…，n)代表某地区 n年的样本数据；A={a1，a2，…，am}代表样本所有因素的集合，其中 ai(i=1,2,…，15)代表 15个商品住宅需求影响因素；D代表商品住宅需求（分类决策属性）。任意给定N维欧式空间中两点，记作xi和xj，其距离为：

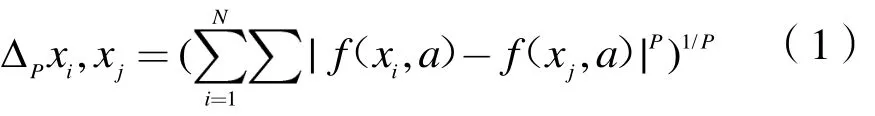
其中，f(x，a)为对象x在属性a上的取值。对于U上任意样本xi，其δ邻域为δ={x|x∈U,Δ(x,xi)≤δ}，其中 δ≥0。N被定义为 A的邻域关系，则NDT=(U，N，D)是商品住房需求影响因素邻域决策系统，N个等价类（因素集）则根据D对U划分而来：{x1，x2，…，xN}，B⊆A，邻域关系NB由B得到，那么在决策D中，B的NB下（NBD）、上近似边界及决策边界BN(D)分别为：

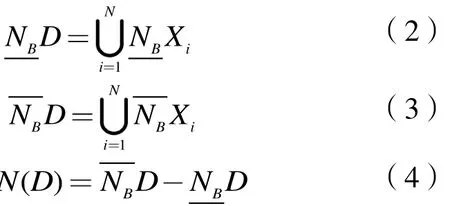
式中，

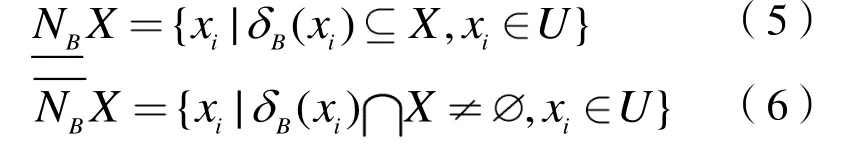
对于条件属性B，商品住宅需求D的依赖度为：

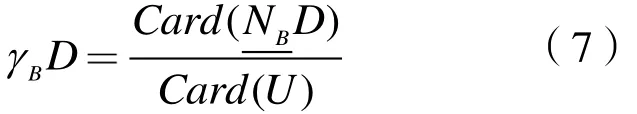
对于商品住宅需求D，条件属性a的重要性为：

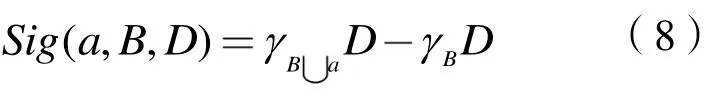
依据商品住宅需求D计算的各属性重要性，由大到小进行排列，在约简集合中加入选择重要度大的属性值，直到属性重要性Sig(a，B，D)小于重要度下限（通常由ς表示，取0.05或者0.01），则剩余属性不加入约简集合，由此得到某一邻域半径下的属性约简结果。之后，按照一定的步长调整条件属性的邻域半径δ，计算δ不同情况下单个属性重要度，得到相应的属性约简集合。而后，对每个约简集合构建相应的训练集和测试集，并将约简集合中的属性值作为输入指标，商品住宅需求（决策属性）作为输出指标，利用weka软件中的分类功能，采用决策树（C4.5）算法、支持向量机（Support Vector Machine，SVM）和朴素贝叶斯（Naive Bayes，NB）分别对训练集进行处理，再利用测试集计算在三类算法下的分类精度。最后根据约简后的分类精度及属性个数，选取合适的邻域半径值，记录对应的属性约简结果，完成模型的评估，输出最佳约简结果，提取影响商品住宅需求的主要因素。

1.3 约简后商品住房需求预测及模型检验

将约简后的商品住宅需求主要影响因素（输入端）及商品住宅销售量历年数据（输出端）放入BP神经网络中训练，直到拟合优度值接近 1，保存训练好的商品住宅需求预测训练模型。再基于灰色预测模型GM(1,1)预测商品住宅需求主要影响因素时序数据，并通过计算后验差比C（C≤0.65）和小误差概率p（0.70＜p）来评定主要影响因素预测的精确度，训练好的BP神经网络输入端数据则为通过检验的主要影响因素时序数据，以此来预测未来年份商品住宅的需求量。

在此基础上，对比普通BP预测模型（将全部影响因素作为BP神经网络输入指标预测商品住宅需求的模型）和NRS-BP预测模型（将约简后的关键商品住宅需求影响因素作为BP神经网络输入指标进行商品住宅需求预测的模型）的预测平均相对误差，从可靠性角度分析NRS-BP商品住房需求预测模型。

2 算例分析

2.1 数据收集与预处理

本文将江苏省某市统计局有关商品住宅需求的数据作为选用对象，包括2005~2017年该市A区商品住宅需求影响因素a1~a15的数据和商品住宅销售面积D等相关数据，分析这16项数据得到图2和图3。

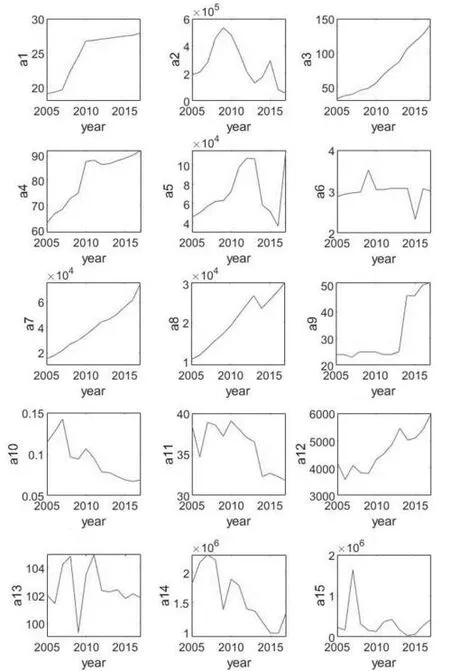
图2 2005~2017年某市A区商品住宅需求全部影响因素统计图

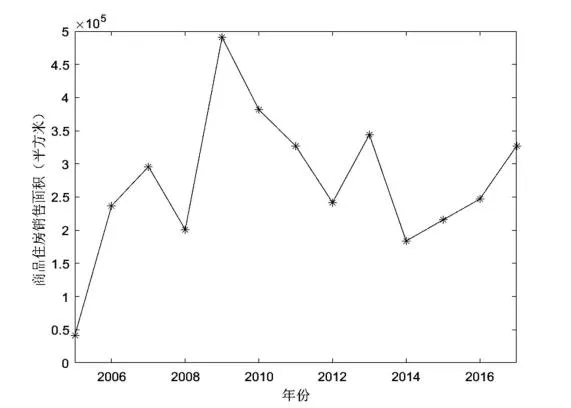
图3 2005~2017年某市A区商品住宅销售面积统计图

由图 2 可知，a1、a3、a4、a7、a8、a9、a12近年来持续增长，a10、a11、a14近年来逐渐下降，而a2、a5、a6、a13和a15变化不明显。由图3可知，某市A区商品住宅销售面积在 2009年高达 490797m2，2009年之后持续下降，2014年达到近 5年最低（183817 m2），在此之后略有回升。

2.2 商品住宅需求影响因素约简

由分析模型第二步可知，邻域δ大小会影响属性约简的样本数量，若δ过小，划分到同一邻域的样本数量较少，商品住宅需求过多依靠该类条件属性，影响因素约简分类的精度会变低，无法实现约简目标，因此选取适宜的δ有利于需求影响因素的约简。李静等[14]在邻域半径的计算上考虑数据标准差，其计算公式为：

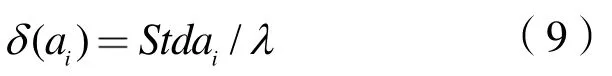
式中，Stdai指的是ai的标差；λ为邻域半径δ计算参数。当样本量较小时，λ取值尽可能在0.5~1.5之间，当样本量较大时，λ取值可调大为2~4。

考虑到本文仅有 12年的样本数据，在实验的基础上确定λ取值区间为0.5~1.15，同时确定重要度下限ς阈值为0.01。在Matlab中运算得到商品住宅需求影响因素约简结果（见表1），任意一个特征集合均可以作为商品住宅需求影响因素集。由表 1可知，当λ取值为0.65时，约简后的指标个数最多，为9个影响因素。当λ取值为1.15时，约简后指标个数仅为2个，即认为a4城镇化率和a6家庭规模主要对商品住宅需求产生影响。

表1 影响商品住宅需求因素约简表

根据约简结果构建14个决策系统{s1，s2，…，s14}，Si={Ri，D}（其中i=1，2，…，14），针对各决策系统Si，划分训练集（用于建模）和测试集（用于评估），输入指标确定为Ri，商品住宅需求D作为输出指标分别输入到 weka软件中，选择分类精度和稳定性都较好的C4.5、SVM和NB算法进行十折交叉检验，分别计算三类算法下的分类精度值，各λ值参数下约简前后三类算法的正确分类比率和属性约简个数结果如图4和图5所示。

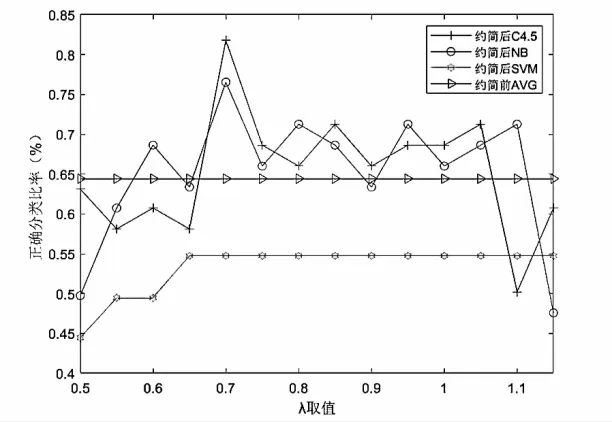
图4 ς=0.01下的分类精度比较

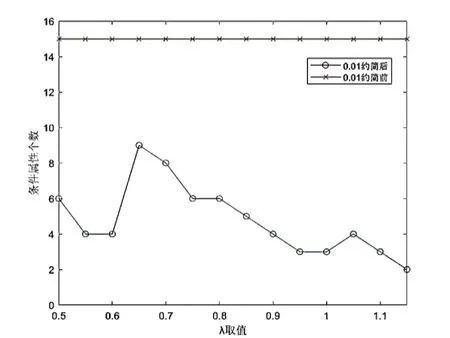
图5 ς=0.01下约简前后的属性个数

由两张图可知，当λ值为0.70，0.85和1.05时，基于 C4.5算法分类器计算得到的正确分类比率为极值处，均大于64.39%（因素约简前平均正确分类比率），选中的属性个数分别为8、5和4，尤其当λ值为0.70时，正确分类率达到最大为81.79%；当λ值为0.70，0.80，0.95和1.10时，基于NB分类器的分类准确率均大于70%，选中的属性个数分别为8、6、3和3，其中当λ值为0.70时，正确分类率达到最大为76.53%；然而，在各λ取值下，基于SVM分类器的正确分类比率均小于64.39%（约简前平均正确分类比率）。通过对比图4和图5可知，属性集中的属性数量增加并不会导致分类准确率的提升，例如约简后属性个数最多时（λ值为0.65时），对应的分类准确率小于基于 C4.5分类器的最大正确分类率。当λ值较小时，属性值的增加提升了正确分类比率，然而随着属性个数的增加，正确分类比率不增反降。综合考虑正确分类比率和条件属性个数，决策系统S5在NB分类器下的结果最好，分类准确率最高（81.79%），因素个数在约简后较少，因此S5为最佳约简情况，即商品住宅需求预测的关键影响因素为a1、a3、a4、a6、a8、a9、a11、a12。

2.3 商品住宅需求预测

在确定影响商品住宅需求的关键因素后，将2005~2017年某市A区8个关键影响因素数据a1、a3、a4、a6、a8、a9、a11、a12作为 BP 神经网络的输入节点，将商品住宅需求作为输出节点，设置隐藏层为 3，利用历年样本数据训练 BP模型。训练结果显示，停止时训练达到140次，训练过程中拟合优度为0.93698，输出值与目标值相近，BP模型的训练效果良好，将模型进行保存。

本文基于灰色预测 GM（1，1）模型，利用Matlab软件预测了2018~2022年某市A区商品住宅需求主要影响因素数据（见表2）。而后，计算各影响因素预测后验差比C及小误差概率p，均达到预测要求，各影响因素预测结果较为可靠。

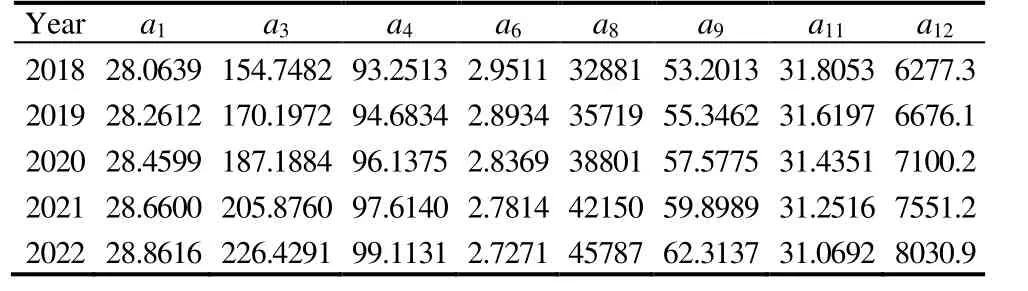
表2 2018～2022年某市A区住宅需求的影响因素预测数据

将表2的数据作为输入指标，输入训练好的BP模型中，预测得到2018~2022年商品住宅销售面积数，分别为 266382 m2、266939 m2、269470 m2、274208 m2和 281659 m2。

2.4 普通BP预测模型与NRS-BP预测模型的比较

通过比较普通BP预测模型及NRS-BP预测模型计算出的预测值与历史值，二者平均相对误差可以直观显示预测效果的差异（见表3）。由表可知，普通BP预测模型的平均相对误差为27.70%，远大于NRS-BP预测模型的平均相对误差7.85%，NRS-BP预测模型更接近真实值。

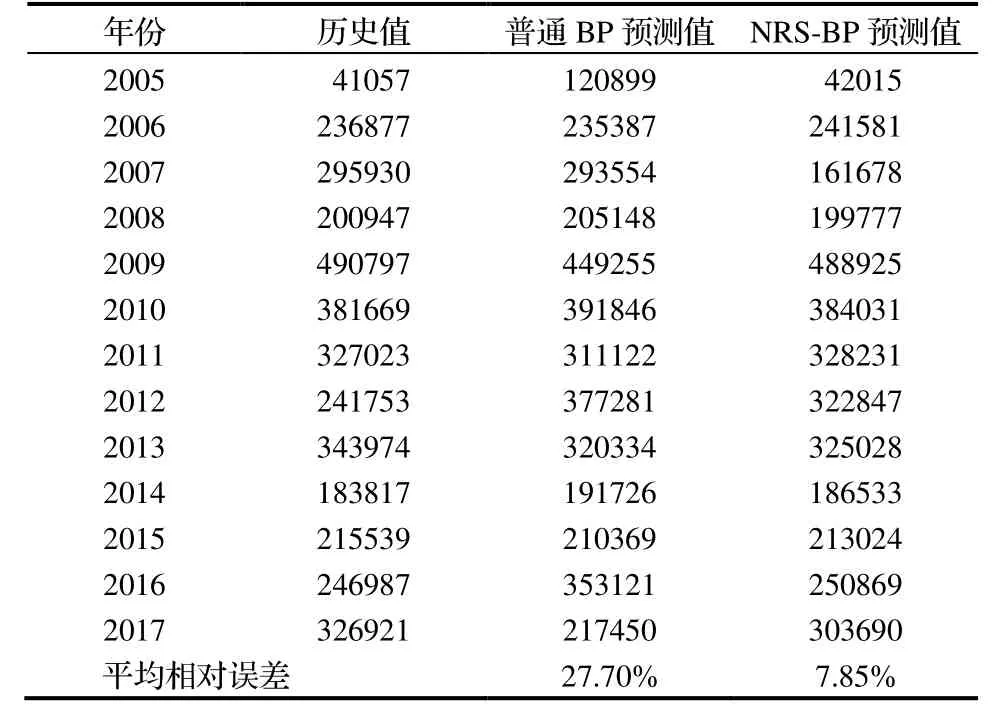
表3 普通BP预测值与NRS-BP预测值的结果汇总表

从模型构建上来看，利用NRS-BP对因素约简可以有效去除原有影响因素之间的信息重叠，最大限度保留BP神经网络输入端信息，从而提高预测模型的训练速度，进一步说明本文选取的 NRS-BP商品住宅需求预测模型相较于普通BP神经网络预测模型具有更高的精度和效率。

3 结语

本文基于NRS和BP神经网络提出一种预测商品住宅需求的方法，通过对某市A区算例分析，验证了本文提出的商品住宅需求预测模型精度较高且可行性较好。但由于国家宏观调控政策及住宅需求中微观层面因素对房地产市场的作用，部分年份的预测值可能会出现一定程度的波动，在今后的住房需求预测中，需要进一步加强对政策影响的量化，同时不断改进微观层面数据获取的手段，将对住宅需求产生影响的各类因素充分考虑在内。