面向数据集覆盖问题的优化算法研究

刘荣鑫

（哈尔滨工业大学 计算机科学与技术学院， 哈尔滨150001）

0 引 言

数据科学时代，基于某些数据集训练学习算法是非常常见的。 通过调查或科学实验，可以前瞻性地收集到数据集，最近已经认识到训练数据集只具有代表性是不够的，如果受训练的系统要很好地处理一些不太流行的类别，则必须包括来自这些类别的足够的例子。 “谷歌大猩猩”强调了这种包含问题的重要性，谷歌早期发布的图像识别算法没有对足够多的深色皮肤图像进行训练，当呈现黑皮肤的非洲裔美国人的图像时，该算法将她识别为“大猩猩”［1］。 还有很多其他此类事件也说明了这个问题。 虽然谷歌对大猩猩事件的解决方案是“删除大猩猩标签”，但更好的解决方案是事先确保训练数据在每个类别中都有足够的条目。 无论分析任务的数据收集模式是什么，必须确保每个对象类别在数据集中有足够的条目。 从数据多样性相关的文献中汲取灵感，将这个概念称为“Coverage”，这样的问题就是数据集覆盖问题［2-3］。 上述示例不是数据科学家采样的问题，他们以某种方式获取了一个数据集，然而没有意识到数据集覆盖问题。 数据集覆盖问题也为对抗性攻击开辟了空间［4］。

数据集覆盖问题和不平衡学习（imbalanced learning）问题类似， 不平衡学习即数据表示和信息提取的学习过程，其中存在严重的数据分布偏差，开发有效的决策边界来支持决策过程，主要有随机采样的方法和代价敏感学习的方法。 使用采样的方法来解决不平衡学习的问题，主要是通过一些机制来改变原始数据集的分布，使得处理后的数据集分布平衡。 在这方面比较有代表性的工作有随机过采样、随机欠采样、基于数据生成的合成采样、基于聚类的采样方法、integration of sampling and boosting。代价敏感学习是利用不同类别的样本被误分类而产生不同的代价，使用这种方法解决数据不平衡问题。很多研究表明，代价敏感学习和样本不平衡问题有很强的联系［5］。

不平衡学习问题主要是处理数据集中标签属性的问题。 而数据集覆盖问题，主要是数据集中的缺乏覆盖的问题，即数据集中的某些条目缺乏覆盖的情况。 例如：对于一个关系型数据集，主要考察数据集中的特征属性，而不是标签属性；考察各特征属性组成的“模式”所覆盖的数据元组个数是否满足特定阈值，提出相应的评价指标，用于评价数据集的覆盖情况，运用相应的算法处理数据集覆盖问题。

综上所述，本文的数据集覆盖问题不同于不平衡问题，使用现有的不平衡学习的方法可能不能很好的处理缺乏覆盖的数据集。 本文研究分析了已有获取MUP 的三种算法的优缺点以及适用场景；结合关联规则挖掘相关研究以及搜索算法的思路，并提出了针对DeepDiver 算法的改进算法FastDeepDiver算法，它能够更快地识别到未覆盖模式并更快地获取MUP，从而过滤掉更多的节点；提出了计算coverage 算法面，对数据稀疏问题以及位图过大、内存不足问题的解决思路。

1 数据集覆盖问题相关算法研究与优化

1.1 数据集覆盖问题相关定义

给定一个数据集D，以及d 个低维分类属性A ＝｛A1，A2，…，Ad｝。 如果属性值是连续的或者高基数的，考虑用桶化的方法将其转换为离散属性。 对于图像，比如说肤色，可能需要先进行图像的肤色相关的标注，想办法转换为离散属性的形式。 每个元组t ∈D 是一个向量，对于所有i ＝1，…，d，Ai的值为t［i］。 此外，数据集还包括包含目标值的“标签属性”Y ＝｛Y1，Y2，…，Yd｝，覆盖问题中不考虑标签属性。 数据集覆盖问题的相关定义如下：

（1）模式（Pattern）。模式P 是大小为d 的向量，其中P［i］ 是X（意味着其值未指定） 或者是属性Ai的值。 将值为X 的元素命名为非确定性元素，将其他元素命名为确定性元素。 一个元组t 匹配模式P（写为M（t，P）＝T），如果对于所有的i，若P［i］ 是确定性的，t［i］ 等于P［i］；否则M（t，P）＝F。

（2）Coverage。 给定具有基数c ＝｛c1，c2，…，cd｝的d 个属性的数据集D，以及基于c 和d 的模式P，模式P 的coverage 是D 中与P 匹配的元组数。 形式上：cov (P，D) ＝

（3） 覆 盖／未 覆 盖 模 式（Covered／Uncovered Pattern）。 如果模式P 的覆盖大于或等于指定的覆盖阈值τ，则称模式P 为覆盖模式，即cov (P，D) ≥τ。 否则，模式P 被称为未覆盖模式。

（4）父／子模式（Parent／Child Pattern）。 如果可以通过用X 替换P2中的一个确定性元素（比如P2［i］） 来获得P1，则模式P1是模式P2的父模式，可以等效地说P2是模式P1的子模式。

（5） 极 大 未 覆 盖 模 式（Maximal Uncovered Pattern （MUP））。给定阈值τ，如果cov (P ) ＜τ（未覆盖），且对于P 的任意父模式P｀，cov (P｀ ) ≥τ（覆盖），则P 为极大未覆盖模式。

（6） MUP 识 别 问 题（ MUP Identification Problem）。给定在具有基数c的d 个属性上定义的数据集D，以及覆盖阈值τ，找到所有最大未覆盖模式M 集合。

1.2 对现有获取MUP 算法的分析与研究

获取MUP，即解决MUP 识别问题。 获取MUP的算法是基于遍历模式图的方法。

模式图（Pattern graph）：令P 为在基数为c 的d个属性上定义的所有可能模式的集合。 P 的模式图是图G（V，E），其中V ＝P。 具有父子关系的每对节点P 和P｀之间都有一条边。 每个边缘位于相邻级别的两个节点之间，父节点比子节点小一级。

如图1 所示，为3 个二元属性的模式图，二元属性即每个属性的属性值可以取0 或1。 下面将通过该模式图示例对已有的获取MUP 算法进行分析，并提出改进算法。

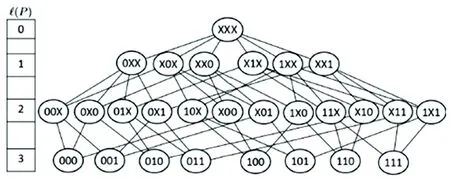
图1 3 个二元属性的模式图Fig. 1 The pattern graph of three binary attributes dataset

1.2.1 自顶向下算法（Pattern-Breaker）分析

自顶向下的算法类似极大频繁项集挖掘中的MaxMiner 算法，采用了广度优先遍历的搜索策略［6］。 它从最一般的模式开始，不断地一层一层地生成更具体的子模式，并利用coverage 的“单调性”属性来过滤掉模式图中的部分节点。 图1 的模式图转换为一个树形图，如图2 所示。

自顶向下算法利用单调性过滤掉部分子模式图，来减少获取MUP 所消耗的时间，但是这个算法在它找到未覆盖模式前，需要遍历模式图中的已覆盖区域的节点，计算这些节点的coverage，它的运行时间取决于模式图中已覆盖区域的大小。 因此，如果模式图中一大片区域都是已覆盖的，那么自顶向下的算法运行时间就很长，性能较差。

图2 自顶向下算法树形图Fig. 2 Thetree graph of Pattern-Breaker

1.2.2 自底向上算法（Pattern-Combiner）分析

自底向上算法参考频繁项集挖掘中从特殊到一般的思路，它自底向上地遍历模式图，同样用单调性来避免遍历整个模式图，一旦找到了一个已覆盖模式，就可以过滤掉这个分支。 自底向上算法将模式图转化为一个森林，并通过相应的规则，来保证每个候选节点只生成一次，如图3 所示。

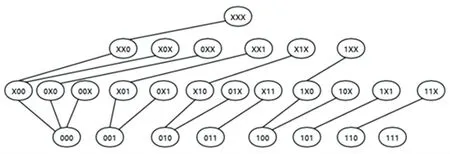
图3 自底向上算法森林图Fig. 3 The forest graph of Pattern-Combiner

自底向上算法先遍历未覆盖区域的节点，所以如果模式图中大部分节点都是未覆盖的，那么该算法的性能较差。 同时，由于它最开始需要通过倒排索引的方式计算第d 层的各个节点的coverage， 而对d - 1 层到第0 层的节点的coverage，只需要根据其子节点得到。 所以，自底向上算法适用于属性基数较小，且阈值较小（大部分节点都是已覆盖的）的情况。 自底向上的算法对于属性基数较大的数据集，运行性能差。 原因：①属性基数大，第d 层的模式节点很多。 ②根据子节点计算自身的coverage，所以基数变大后每个节点的计算时间也会增加（可能造成严重哈希冲突）。 对于属性个数多，属性基数小的数据集，使用自底向上的算法比较好，当然也得综合考虑阈值。

1.2.3 DeepDiver 算法分析

当处于模式图的中间层数时，这两个算法都表现不佳，因为它们都需要遍历大约一半的模式图。

DeepDiver 算法采用类似极大频繁项集挖掘中MAFIA 算法的思路［6］，考虑使用深度优先遍历的搜索策略（扩展节点方式同自顶向上算法），以更快地找到未覆盖模式，通过建立已获得的MUP 集合的倒排索引，来高效地过滤掉MUP 的祖先节点以及后代节点。 DeepDiver 算法对于属性基数大的数据集大部分情况运行时间比自底向上算法少，且更稳定。

1.3 获取MUP 的改进算法——FastDeepDiver 算法

DeepDiver 算法利用了深度优先搜索的方法尽快找到MUP，目的是更快地找到未覆盖模式节点。深度优先搜索扩展的方向不一定是较优的搜索方向，有爬山法最佳优先搜索等方法用于优化深度优先搜索策略。

考虑这样一个示例，一个有3 个二元属性的数据集D，其只有一个数据元组100，设定阈值为1，可以得XX1 为MUP，考虑使用DeepDiver 算法来获取MUP，如果它是通过XXX→1XX→10X→101 的路径进行深度优先搜索，那么当遍历到101 时才发现其为未覆盖模式，从101 开始向上找MUP，依次替换它的确定性元素为X，当替换第一位为X 时，得到父节点X01，计算X01 的coverage，得到其为未覆盖模式，继续替换得到X01 的父节点XX1，计算XX1 的coverage，得到其为未覆盖模式，继续替换得到XX1的父节点XXX，计算XXX 的coverage，得到其为已覆盖模式，因为XX1 只有一个父节点，从而得到XX1 为MUP。 然而，如果它是按照XXX→XX1 的路径进行深度优先搜索，那么在遍历到XX1 时发现它是未覆盖模式，从而发现它是MUP，那么当后面遇到10X 以及它的后代节点直接被MUP 的倒排索引过滤了。 从上述例子推理可知，属性个数越多，如果能在更浅的层找到未覆盖模式，从而找到MUP，那么能够过滤掉的节点就会更多，而且在往上找MUP 的过程，也能避免计算一些已覆盖父节点的coverage。 也就是说，在更浅的层更早地发现MUP，就能更快地找到MUP，从而过滤掉更多的节点，可以减少在找到未覆盖模式节点后，向上找遍历的祖先节点个数。 因此，考虑结合爬山法和最佳优先搜索策略对深度优先搜索进行优化，提出对DeepDiver算法的改进算法FastDeepDiver 算法。

先计算模式图中第一层节点的coverage，如果第一层的各节点有一个未覆盖模式节点，那么按照节点的coverage，由大到小的顺序依次压入栈中，再进行深度优先搜索；如果第一层各节点都是已覆盖的，那么考虑从第一层的节点生成第二层的节点，计算第二层各节点的coverage，再按照第二层各节点的coverage 由大到小的顺序依次压入栈中。 这样就保证了深度优先搜索最初前进的方向为最优的方向。 FastDeepDiver 算法的伪代码如下：

Algorithm 2FastDeepDiver

Input：DatasetDwithdattributes having cardinalities c and thresholdτ

Ouput：Maximal uncovered patternsM

1： LetS ＝an empty stack

2： compute the coverage of each node in level 1 and store them in a hash tableT

3：isLevelOneHasUncovered ＝a flag indicating if there is a uncovered

node in level 1

4：if isLevelOneHasUncovered ＝＝true then

5： push the nodes in level 1 toSin descending order of coverage

6：initialLevel ＝1

7：else

8： clear hash tableT

9： compute thecoverage of each node in level 2 and

store them in a hash tableT

10： push the nodes in level 2 toSin descending order of coverage

11：initialLevel ＝2

12：end if

13：level ＝initialLevel

14： whileSis not empty do

15：P ＝pop a node fromS

16： uncoveredFlag ＝a flag indicating ifPis uncovered

17：iflevel ＝＝initialLevelthen

18：cnt ＝T.get（P）

19：uncoveredFlag ＝cnt ＜τ

20： else ifPis dominated byMthen

21： continue

22： else ifPdominatesMthen

23：uncoveredFlag ＝false

24： else

25：cnt ＝cov（P，D）

26：uncoveredFlag ＝cnt ＜τ

27： end if

28： ifuncoveredFlag is truethen

29： LetS′ ＝an empty stack

30： pushPtoS′

31： whileS′is not empty do

32：P′ ＝pop a node fromS′

33：K ＝generates parent nodes ofP’ by replacing one deterministic cell withX

34：flag ＝0

35： forP″∈Kdo

36：cnt′ ＝cov（P″，D）

37： ifcnt′ ＜τthen

38： pushP″toS′

39：flag ＝1 ； break

40： end if

41： end for

42： ifflag ＝＝0 then

43： addP′toM

44： end if

45： end while

46： else

47：Q ＝generates nodes onPand c based on Rule 1

48：ifQ.size＝＝0 then

49：level - -

50： else

51：level ＝level + Q.size

52： end if

53： pushQtoS

54： end if

55： end while

56： returnM

第13 行中的level变量是判断当前栈中弹出的节点是否是处于一开始计算过的层中，如果是，可以通过哈希表直接得到节点的coverage。

有研究证明没有多项式时间复杂度的算法可以完成MUP 的枚举，考虑一个有n个数据元组和n个二元属性的数据集D，这些属性的属性值只有对角线上的值为1，其他取值都为0，即∀i∈［1，n］，有ti［i］＝1 且∀j≠i，有ti［j］＝1，如表1 所示。

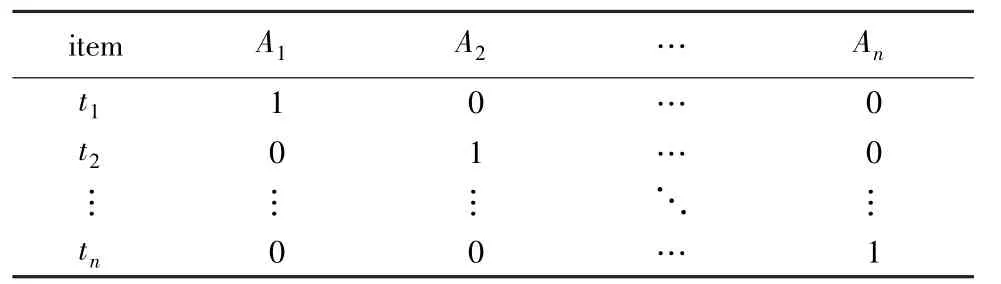
表1 示例数据集Tab. 1 The constructed dataset

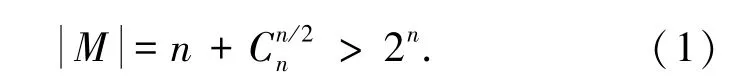
可以做一个估算，考虑上述数据集，因为整个模式图中所有节点的个数为：

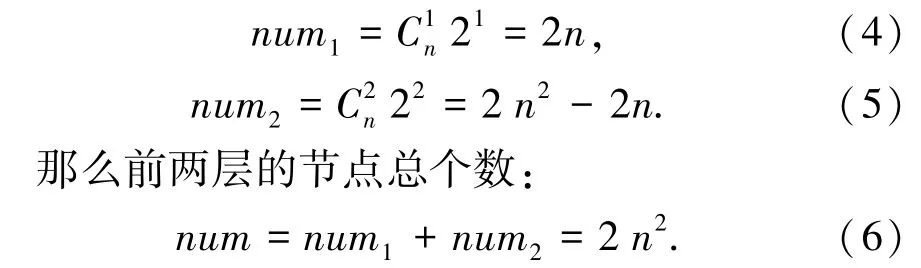
当n ≥7 时，2n＞2 n2，即MUP 的个数大于前两层的节点的总个数，找到一个MUP 后，可以过滤掉的节点个数显然不止一个，而且当n 越来越大时，前两层的节点个数num ≪total，计算的前两层节点coverage 的个数也远小于能够通过MUP 过滤掉的节点个数。

DeepDiver 算法相对于自顶向下算法以及自底向上算法来说，其优点在于当阈值不是特别大或者阈值不是特别小时，它能过滤的节点个数更多，性能更好， 相对来说更加稳定。 本文提出的FastDeepDiver 算法，能够更快地找到未覆盖模式，从而更快地找到MUP，过滤掉更多的节点，它在大多数情况下，性能比DeepDiver 算法更好、更稳定。

1.4 计算coverage 算法的改进方法

coverage 的计算方法，将数据集转换成属性值的倒排索引。 该方法类似频繁项集挖掘中的BitTableFI 算法，将数据库转换成高度压缩的Bitmap的形式，通过基于Bitmap 上的位与运算，快速计算出候选集的支持度，从而大大减少了挖掘过程中扫描数据库的时间开销。 计算coverage 的方法利用了倒排索引，从而也建立了一个Bitmap。

考虑一个示例数据集，其有3 个二元属性，其中有5 个数据元组，t1为010，t2为000，t3为001，t4为101，t5为010，可以得到倒排索引如表2 所示。

得到了这样的倒排索引后，根据与运算和点积运算的方法来获得一个模式的coverage。 其中， 位向量的总个数为cd，c 即属性的基数，d 为属性个数，每个位向量的长度为O（n），因此存储所有位向量需要O（cdn）。

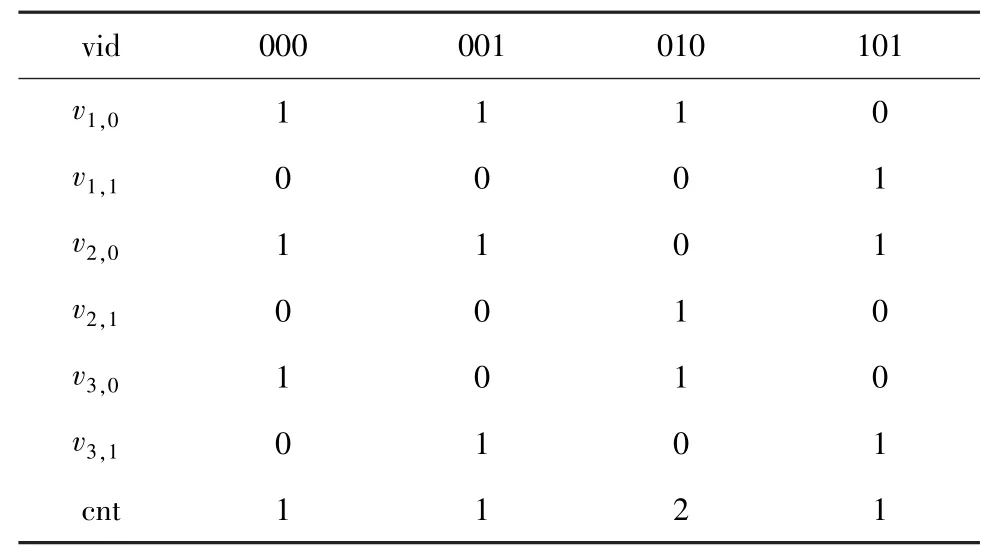
表2 示例数据集倒排索引Tab. 2 The inverted indices of constructed dataset

上述方法存在两个问题：①如果这个倒排索引比较稀疏，即Bitmap 中大部分值都为0 的情况，将会带来很多无效的与操作。 ②虽然Bitmap 极快地提高了coverage 的计算效率，但是同样也带来了一个问题，即极大的内存需要，如果数据元组类型太多，可能无法全部读入内存。 对于以上两个问题，本文提出了以下3 个改进方法。

（1）提高与运算效率的方法。 考虑引入一个辅助内存，比如要计算模式001 的coverage，先计算v1，0AND v2，0的结果，再用这个结果去和v3，1做与运算，想要在这个过程中过滤掉很多0 的位，就可以考虑只存储v1，0AND v2，0结果中为1 的位的下标集合N，表2 的例子中N ＝｛0，1｝，0 表示000 的位置下标，1 表示001 的位置下标，只需要考察v3，1中处于N 中的下标处是否为1 即可。 如果是0 则从N 中删除这个下标，即此时只需考察v3，1中下标为0 和1位置的值，得到N ＝｛1｝，最后做与运算得到结果为向量｛0，1，0，0｝， 再与cnt 做点积运算， 即可得到001 的coverage 为1。

（2）压缩Bitmap 的方法。 若Bitmap 中0 特别多，不妨考虑在倒排索引中只保存位置为1 的下标，即每个vi，j中只存储下标值，为下标的集合，比如表2 的例子中，v1，0为｛0，1，2｝。 Bitmap 中的与运算转换成求交集运算，即下标求交集运算，得到的结果再转换为位向量的形式，再与cnt 做点积即可。 这样的方法压缩了Bitmap 的存储空间，但是增加了运行时间。

（3）划分Bitmap 的方法。 若Bitmap 中数据元组类型特别多，这样的倒排索引无法全部存入内存，可以考虑把Bitmap 按元组（即列索引）进行划分，比如表2 中的Bitmap，如果考虑把它划分为两个部分，则v1，0从｛1，1，1，0｝划分为｛1，1｝和｛1，0｝ ，相应的cnt 划分从｛1，1，2，1｝ 划分为｛1，1｝ 和｛2，1｝，各个部分读入内存后，各自做与运算得到的结果与cnt 的该部分做点积运算得到covi，再把这些cov 加起来就得到了coverage。

2 算法结果及分析

2.1 数据集与实验运行环境

（1）数据集：①AirBnB 数据集，收集了785 331条数据元组以及15 个属性，其中一个属性为三元属性，其他属性都是二元属性。 ②BlueNile 数据集，BlueNile 是全球最大的线上钻石零售商，收集了116 300条数据元组，数据集包括7 个分类属性，分别是形状、切割、颜色、透明度、抛光度、对称性和荧光，各自的属性基数为10、4、7、8、3、3、5。

（2）实验运行环境：①硬件环境，2.80GHz i5 CPU 以及12GB 内存。 ②软件环境，Windows 10 操作系统，通过Java 实现算法在IntelliJ IDEA 集成环境中运行。

AirBnB 数据集由于其属性个数较多，模式图大，用于对比获取MUP 的算法的性能；BlueNile 数据集由于其属性基数较大，主要用于验证自底向上算法对于属性基数较大的数据集性能较差的推理。

2.2 获取MUP 算法性能对比实验

本文主要从阈值τ 变化以及数据元组个数n 的变化来进行获取MUP 算法的性能。

2.2.1 只改变阈值性能对比实验

只改变阈值，而不改变属性个数以及数据元组个数。

（1）采用AirBnB 数据集，取前10 个属性进行实验，其中有一个属性为三元属性，其他属性都为二元属性，数据元组个数为785 331 个，约80 万条数据元组，阈值从8 ～80 000，实验得到如图4 的实验结果，随着阈值从小变大，模式图中由大部分模式都是已覆盖的到大部分都是未覆盖的，所以自顶向下算法运行时间由长变短，自底向上算法运行时间由短变长，DeepDiver 算法和FastDeepDiver 算法运行时间都是先变长后变短，从图中可以看到，自底向上算法大部分情况运行时间都较短。

（2）采用属性基数较大的BlueNile 数据集进行实验。 BlueNile 数据集一共有116 300 条数据元组，且有7 个属性，阈值从1 ～1 000。 实验得到如图5所示的结果。 可以看到，由于BlueNile 中属性基数较大，自底向上的算法大部分情况运行时间都较长。

（3）由上述实验可以看出，DeepDiver 算法和FastDeepDiver 算法有更好的鲁棒性，更加稳定。 接下来利用AirBnB 数据集验证FastDeepDiver 算法和DeepDiver 算法，本文采用AirBnB 数据集中的前13个属性，其中12 个属性为二元属性，1 个属性为三元属性，数据元组个数n 为785331，阈值从8 ～80 000，实验得到如图6 所示的结果，可以看出FastDeepDiver 算法大部分情况都比DeepDiver 算法性能更佳，因为FastDeepDiver 算法能够更快地寻找到未覆盖模式（在更浅的层），从而找到MUP，从而过滤更多的节点。 当阈值设定特别小时，DeepDiver算法运行时间比FastDeepDiver 算法稍短，原因是阈值特别小时，模式图中大部分区域都是已覆盖的，相对DeepDiver 算法，FastDeepDiver 算法比较难在更浅的层找到未覆盖模式，因为FastDeepDiver 算法一开始需要先计算前两层（可能不用计算第二层）的节点的coverage，且对这些节点按coverage 排序，所以当阈值特别小时， FastDeepDiver 算法相对DeepDiver 算法没有提升。 从实验可以得出，大部分情况下FastDeepDiver 算法是优于DeepDiver 算法的，其鲁棒性更佳。

图4 AirBnB 数据集-只改变阈值（n＝785 331，d ＝10）Fig. 4 AirBnB：varying threshold（n＝785 331， d ＝10）

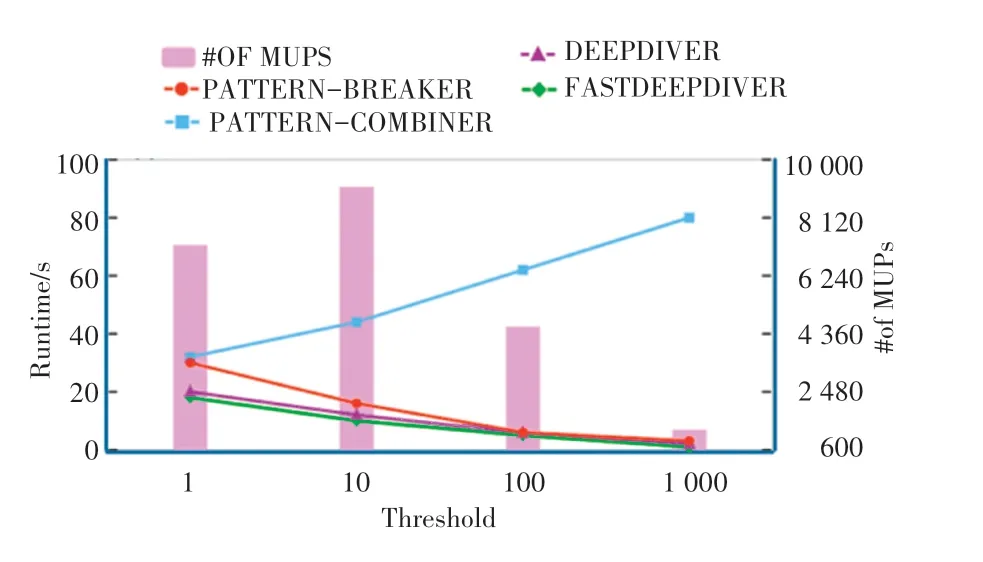
图5 BlueNile 数据集-只改变阈值（n＝116 300，d ＝7）Fig. 5 BlueNile：varying threshold（n＝116 300，d ＝7）

2.2.2 只改变数据元组个数性能对比实验

本部分考察当数据元组个数变化时，各个获取MUP 算法运行时间变化情况。 使用AirBnB 数据集，取前10 个属性进行实验，其中有一个属性为三元属性，其他属性都为二元属性，阈值取5 000，数据元组个数从8 000～785 331，得到如图7 所示的实验结果。

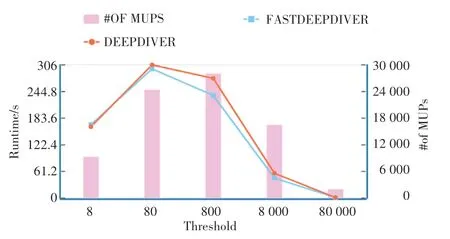
图6 AirBnB 数据集-只改变阈值（n＝785331，d＝13）Fig. 6 AirBnB：varying threshold（n＝785331，d ＝13）

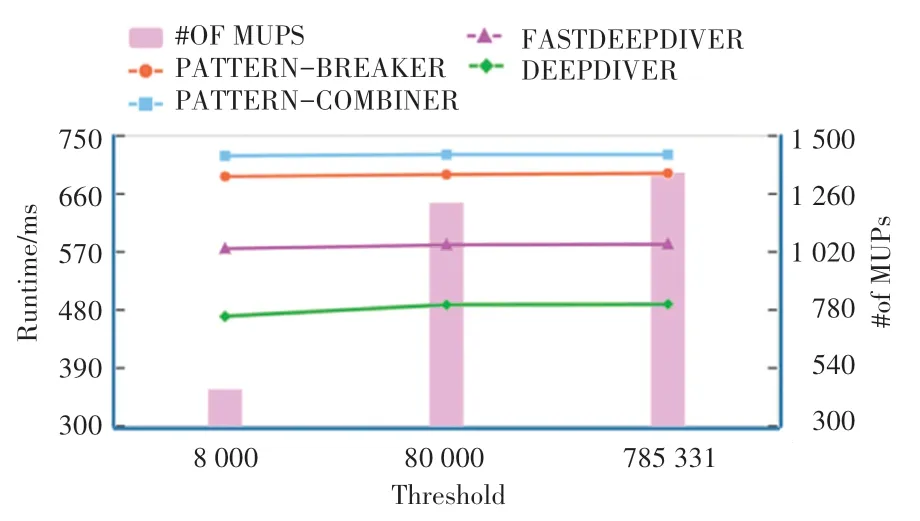
图7 AirBnB 数据集-只改变数据元组个数（threshold＝5000，d＝10）Fig. 7 AirBnB：varying data size（threshold＝5000，d ＝10）

从图7 可以看出，各个算法运行时间几乎不变化，因为数据元组个数大小只会影响计算coverage的倒排索引的大小，但当数据元组个数为8 000 时，数据集几乎所有元组类型都已经包含到了，所以对倒排索引占内存大小几乎没有影响，只影响cnt 向量中各位的值。 自底向上的算法只有在计算最底层的节点的coverage 时需要从倒排索引中计算，其受数据元组个数影响更小。

3 结束语

本文针对数据集覆盖问题，在已有定义的基础上，分析并提出了一系列的改进优化算法。 首先，分析了已有的获取MUP 算法的优缺点及适用场景；其次，结合关联规则挖掘相关研究以及搜索算法的思路，研究并提出了针对DeepDiver 算法的改进算法FastDeepDiver 算法，提出了计算coverage 算法对数据稀疏问题以及位图过大内存不足问题的解决思路。

通过实验分析了各个获取MUP 的算法的性能，并验证了FastDeepDiver 算法相对于DeepDiver 算法的改进效果。

未来考虑结合不平衡学习中的一些方法，用于处理数据集覆盖问题。