基于MATLAB数据分析方法在空调器实验数据处理中的应用
樊小波
(青海高等职业技术学院,青海 乐都810799)
【关键字】MATLAB;空调器;数据分析;多元回归分析
0 引言
随着气候的变化,空调已成为生活中不可或缺的一部分,尤其是在我国的南方地区,空调更是起到至关重要的作用。而在设计空调系统时,必不可少的环节是压力、温度的测试,因为在空调系统设计时要根据压力、温度的测试数据和制冷剂的压焓图,将得出的数据代入理论计算公式,从而得出空调系统的理论单位制冷或制热能力。
1 制冷剂压焓图
压焓图,指压力与焓值的曲线图。常用于制冷剂分析。该图纵坐标是绝对压力的对数值log p(图中所表示的数值是压力的绝对值),横坐标是比焓值h。

图1 压焓图示意图
压焓图曲线的含义可以用一点 (临界点)、二线(饱和液体线、饱和蒸汽线)、三区(液相区、两相区、气相区)、五态(过冷液状态、饱和液状态、过热蒸汽状态、饱和蒸汽状态、湿蒸汽状态)和八线(等压线、等焓线、饱和液线、饱和蒸汽线、等干度线、等熵线、等比体积线、等温线)来概括。
2 基于压焓图的理论热力计算
单位质量制冷量q0指的是1 kg制冷剂在蒸发器内从被冷却物吸收的热量,理论计算公式为q0=h1-h4。
单位体积制冷量qv指的是压缩机吸入了1 m3制冷剂蒸汽后在蒸发器中产生的制冷量,理论计算公式为qv=q0/v1=(h1-h4)/v1。
制冷剂质量流量理论计算公式为MR=Q0/q0
制冷剂体积流量理论计算公式为VR=MR*v1
单位冷凝负荷qk指的是1 kg的制冷剂在冷却和冷凝过程中放出的热量,理论计算公式为qk=h2-h3
单位理论压缩功w0指的是压缩机压缩输送1 kg制冷剂所消耗的压缩功,理论计算公式为w0=h2-h1
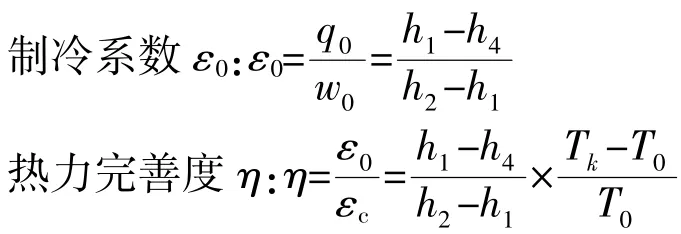
制冷剂在制冷系统中的理论循环如图2所示,压缩机对制冷剂的压缩过程为图中a-b阶段,制冷剂在冷疑器中的冷凝过程是b-c阶段,节流过程为c-d阶段,制冷剂在蒸发器中的蒸发过程是d-a阶段[1]。

图2 制冷剂循环过程
3 基于MATLAB的数据回归分析
在MATLAB中,stepwise函数的作用就是逐步回归需要进行分析的变量,stepwise函数是一个交互工具,它使用矩阵X的列向量组成的子集来建立一个对y进行预测的回归模型。
本文制冷剂采用的是R404A,其中推导数据采用的是制冷剂参数,该参数由计算机软件提供。再基于MATLAB的回归分析能力,对制冷剂R404A的各个数据(气体粘度系数、密度和压力、温度之间的函数关系式)进行多元线性回归,以此R404A在不同温度、压力下的参数值。
从压焓图的基本理论可得,在温度和压力已知条件下,制冷剂比容值可以推导出来,而密度和比容互为倒数,因此可将其作为温度与压力的函数。再根据制冷剂计算软件得出的数据,建立R404A密度ρ与压力p、温度t的函数关系式,如下式所示。

其中,a5、b5、c5、d5、e5、f5、g5为待定系数。
根据上式,基于MATLAB,拟合R404A关于压力和温度的密度关系式,图3为密度拟合曲线和误差曲线,拟合后的均值误差值为0.28%。
制冷剂计算机软件可以统计出来R404A的参数数据,依据这些数据可以建立R404A气体粘度系数v与压力p、温度t的函数关系式,如下式所示。

其中,a6、b6、c6、d6、e6、f6、g6为待定系数。
根据上式,拟合R404A的温度和压力的关系式,该温度和压力是关于R404A的气体粘度系数的。图4为密度拟合曲线和误差曲线,拟合后的均值误差值为0.86%。数据进行拟合后,与参考数据的均值误差可以控制在1%以内。
基于以上建立的空调控制系统的温度、压力和环境工况,以及压缩机运行频率间的数学模型和R404A材料参数关系式,就可以在特定环境工况下测试出空调系统的温度、压力数据,再由此推导出普通环境工况下的温度和压力值,以及相应的制冷剂材料参数,可以为空调系统的设计提供相应的数据和CAE仿真提供材料参数输入。
4 结论
本文基于MATLAB的回归分析能力,建立了空调制冷系统的数学模型,以制冷剂R404A为例,多元非线性回归分析了R404A的气体粘度系数和密度的参数,从分析结果得出与参考值之间的均值误差可以控制在1%以内,且精度较高。
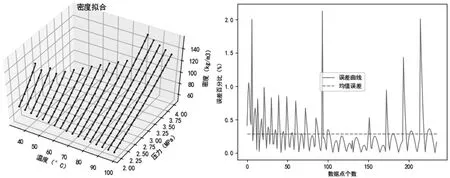
图3 密度拟合曲线和误差曲线

图4 密度拟合曲线和误差曲线

