堆排序的构造方法探究

杜双敏

摘要：堆排序作为一种内排序算法，其特点是将待排序记录R[1..n]看成一棵完全二叉树的顺序存储结构，利用完全二叉树中孩子结点和双亲结点之间的内在关系，在当前无序区中选择关键字最小（或最大）的记录输出，依次得到一个有序序列。堆排序需要解决的两个问题：一是如何将一个无序序列建成一个堆;二是在输出堆顶元素之后，把剩余元素调整成为一个新堆。堆排序对少量的记录来说，其优点不明显，但对大量记录来说是很有效的。

关键词：堆排序;完全二叉树

中图分类号：TP399 文献标识码：A

文章编号：1009-3044（2020）27-0067-03

开放科学（资源服务）标识码（OSID）：

排序就是确定一种排列[Rj1，Rj2，…，Rjn]，设含n个记录的文件{R1，R2，…，Rn】，与其相应的关键字为{k1，k2，…，kn），使得与它们相应的关键字满足递增（或递减）关系，即：Kj1≤Kj2≤…，Kjn这种操作过程就称为排序。简而言之，排序就是将一个数据元素（或记录）的任意系列重新排成一个按关键字有序序列。如果在待排序的表中，存在多个相同关键字的记录，经过排序后这些相同关键字记录之间的相对次序保持不变，则称这种排序方法是稳定的;反之，若相同关键字记录之间的相对次序发生了变化，则称这种排序方法是不稳定的。

1964年J.willioms和Floyd提出了堆排序算法，堆排序是一树型选择排序，在其排序过程中的比较次数达到树型选择水平，同时又不增加存储开销。它的特点是将记录R[1..n]看成一棵完全二叉树的顺序存储结构，利用完全二叉树中孩子结点和双亲结点之间的内在关系，在当前无序区中选择关键字最小（或最大）的记录输出。在输出堆顶的最小值（或最大值）之后，便将剩下的n一1个元素的序列重新建成一个堆，则得到n个元素的次最小值（或次最大值），如此反复，便得到一个有序序列，这个过程我们称之为堆排序。

堆排序算法的基本思想可以描述为：对一组待排序记录的关键字，首先是按堆的定义将它们建成一个堆，排成一个序列，从而输出堆顶的最小（或最大）关键字。然后将剩余的n-l个关键字再重新建成一个新堆，通常称为重新调整成堆，便得到次小（或次大）的关键字输出，如此反复，直到全部关键字排序成有序序列。

堆的定义[1]为：

对于一个关键字序列（k1，k2，…，kn】，当满足：

称此序列为堆（heap），其中，i=1，2，…，[n/2]。满足条件①称之为小根堆，满足条件②称之为大根堆。

堆排序需要解决的两个问题：（1）如何将一个无序序列建成一个堆？（2）如何在输出堆顶元素之后，把剩余的元素调整成为一个新的堆？

设记录的关键字集合key={49，38，66，90，75，10，20），下面以其为例，来说明堆的构造和堆的筛选、重建过程。

1 堆的构造

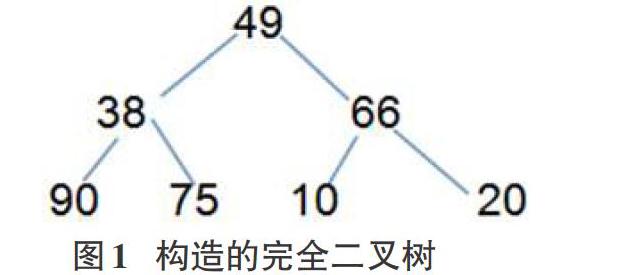
我们可以借助完全二叉树来描述堆。先把关键字集合key={49，38，66，90，75，10，20】构造成一棵完全二叉树。

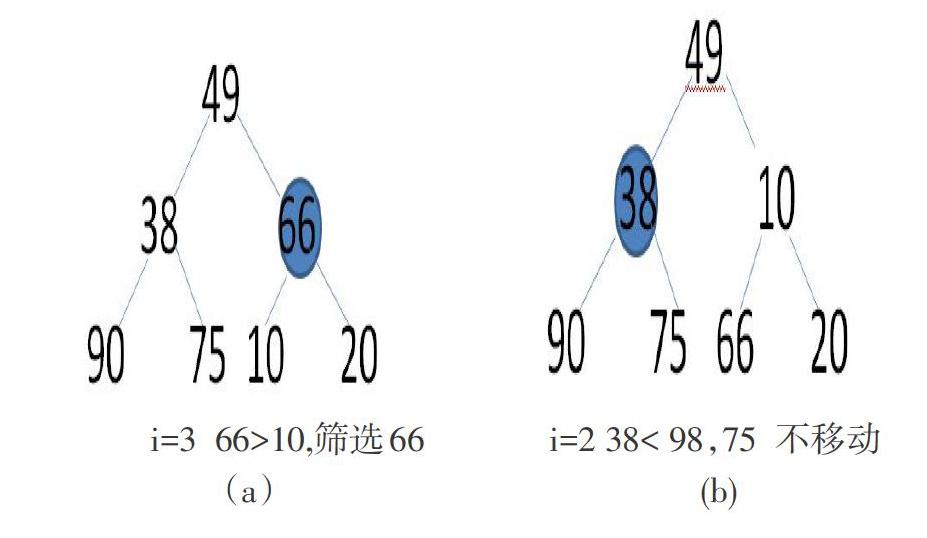
依照Floyd筛选法，从完全二叉树的第i（i=[n/2]）个结点序号开始，对以此结点为根的子树做必要调整，使该子树为堆。然后再分别调整以第i-1，i-2，…，1个结点序号为根的子树。

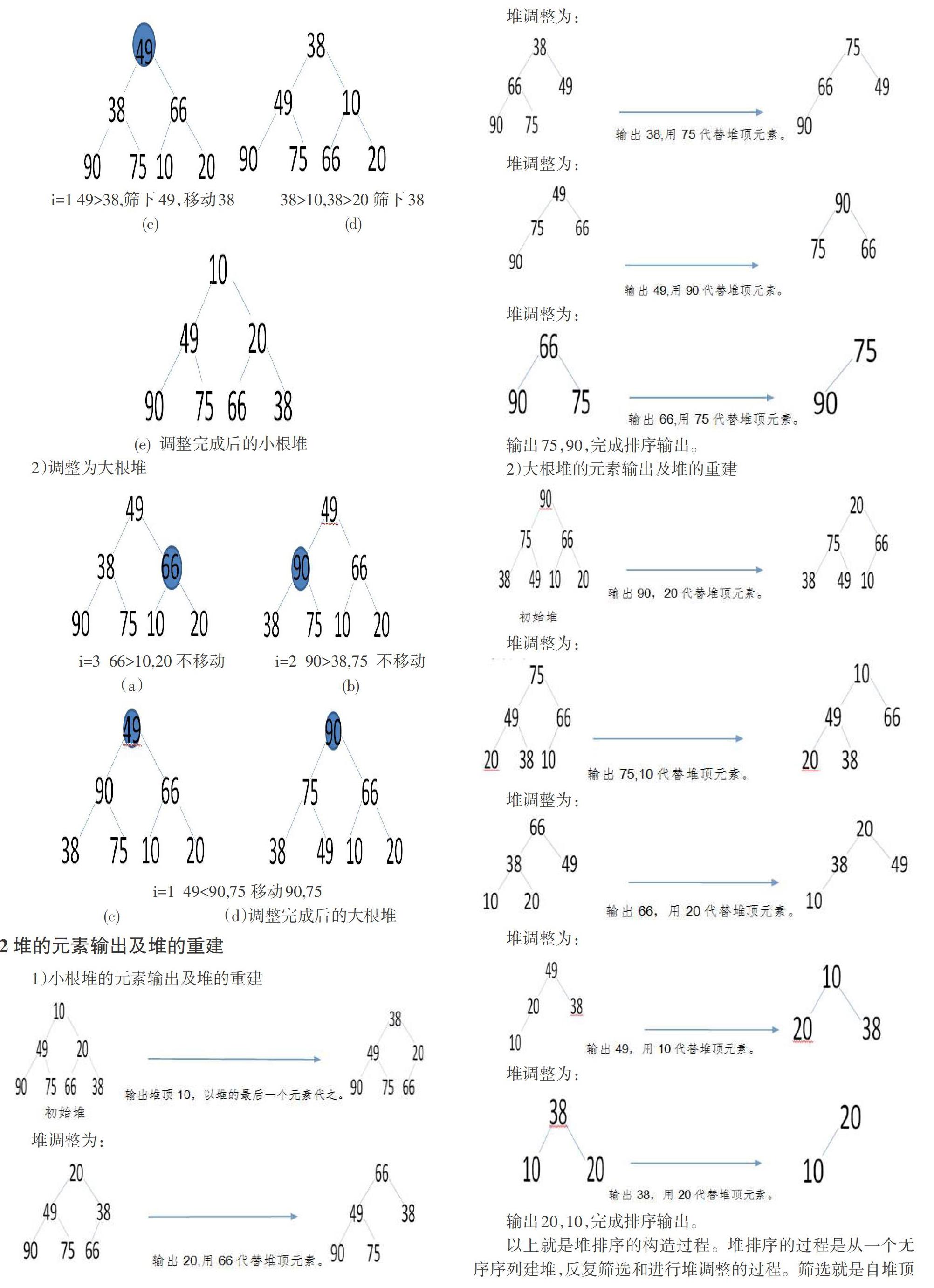
1）调整为小根堆

2）调整为大根堆

2堆的元素输出及堆的重建

1）小根堆的元素输出及堆的重建输出75，90，完成排序输出。

2）大根堆的元素输出及堆的重建

输出20，10，完成排序输出。

以上就是堆排序的构造过程。堆排序的过程是从一个无序序列建堆，反复筛选和进行堆调整的过程。筛选就是自堆頂至叶子的调整过程。堆调整就是输出堆顶元素之后，以堆的最后一个元素（叶结点）代替之。

其算法如下：

Void Heapsort（RecType R[]，int n）

{ int i;

RecType temp;

for（i=n/2;i>=l;i--）

Sift（R，i，n）;

for（i=n;i>=2;i--）

{ temp=R[1];

R[1]=R[i]

R[i]=temp;

sift（R，l，i-l）;}

）

Void sift（RecType R[]，int low，int high）

{ int i=low，j=2*i;

RecType temp=R[i];

While （j<=high）

{ if（R[j].key< R[j+l].key&&j

j++;

if（R[j ].key>temp.key）

{R[i]=R[j]

i=J;

j_2*i;）

else break;1

R[i]=temp;）

3 结束语

堆排序对少量的记录来说，其优点不明显，但对大量记录来说是很有效的。堆排序在最坏的情况下，其平均时间复杂度为O（nlog2n），辅助空间O（1），它不稳定。

参考文献：

[1]严蔚敏，吴伟民，数据结构（C语言版）[M].北京：清华大学出版社，1996.

[通联编辑：梁书]