对城市煤炭供应过程中煤炭运输车的路径规划

何康佳，何 玲，冯 磊，张光星

( 贵州大学 现代制造技术教育部重点实验室，贵州 贵阳 550025)

煤矿是我国非常重要的能源[1]，城市煤炭供应关乎着城市工业的发展。如何调配车辆进行煤炭运输是一个值得研究的车辆路径规划问题(vehicle routing problem，VRP)。为提高运输系统的运行效率和服务水平，通常会设置多个城市煤炭配送中心。因此，解决多配送站情况下的车辆路径规划问题(multi-depot vehicle routing problem，MDVRP)具有重要的实际意义。RENAUD等[2]以最小化总物流成本为目标，提出以车辆容量和行驶里程为约束条件的MDVRP，并设计了禁忌搜索算法进行求解。KUO等[3]针对具有装载成本的MDVRP，设计了三阶段的变领域搜索算法进行求解。RAN等[4]研究了多承运商合作情形下的MDVRP，并提出一种两阶段贪婪启发式算法。

从现有的研究来看，针对最小化碳排放量的车辆路径规划问题的研究多考虑单个配送站的情形，而对于多配送站的物流配送系统下的车辆路径规划问题研究较少。多配送站是物流配送系统中普遍使用的配送方式。因此，研究多个配送站情形下以最小化碳排放量为目标的车辆路径规划问题更具有实际意义。考虑到车辆的碳排放与行驶里程和实际载重量具有正相关关系[5-6]，将燃料成本和碳排放成本考虑到总物流成本中，提出了以最小化物流成本和行驶距离的多目标多配送站车辆路径规划问题，建立了该问题的混合整数规划模型。进一步针对问题特点，设计了化学反应算法进行求解。仿真实验结果表明，该算法可以有效地解决所提出的问题。

1 问题描述和模型构建

1.1 问题描述

一个城市煤炭配送系统有m个配送中心，n个消耗点。配送车辆的最大载重量为Q，考虑到车辆油耗和司机工作负荷的约束，配送车辆的行驶距离不超过L。要求在满足车辆载重和行驶距离的约束条件下，合理地安排配送车辆和车辆的行驶路径，从而最小化车辆配送的物流成本和行驶距离。一个可行的配送方案需要满足如下条件：

(1)每个配送中心的车辆数目均是有限的。

(2)车辆只能从配送中心出发，沿着1条配送路线将装载的货物送达指定煤炭消耗点，并最终回到原配送中心。

(3)1辆配送车辆可以服务多个煤炭消耗点，但每个煤炭消耗点仅被1辆车服务1次。

(4)每辆车有容量和最大行驶距离的约束，所有的配送车辆均是同质的。为建立该问题的数学模型，对符号定义如下：

1.2 符号定义

(1)集合

C：消耗点索引集合，C={c1,c2,…,cn}，n个消耗点数量；

D：配送中心索引集合，D={d1,d2,…,dm}，m个配送站数量；

N：配送站和消耗点索引集合，N=C∪D；

K：配送车辆索引集合，K={k1,k2,…,km}。

(2)参数

qi：消耗点i的需求量(0≤qi≤Q)；

dij：任意两点i和j之间的欧式距离，i,j=1,2,…,n,…,m+n；

ω：配送车辆空车净重；

Q：配送车辆的最大装载量；

L：配送车辆的最大行驶距离；

Cf：每辆车的固定成本(包括车辆租赁费、车辆保险费以及司机工资等)；

Cv：车辆单位燃料成本；

φ：单位碳排放的成本。

(3)决策变量

xijk：如果车辆k经过(i,j)值为1，否则为0；

fijk：配送车辆k经过(i,j)时的货物装载量。

1.3 车辆碳排放量刻画方法

已有的研究成果表明，车辆的碳排放量与燃料消耗量具有正相关关系，因此可以利用燃料消耗量刻画其碳排放量[7-8]。考虑到车辆的实际载重量和行驶距离与燃料消耗量的关系，本文采用如下的方法计算燃料消耗量：

(1)

其中：ρ*和ρ0分别为车辆满载和空载时的燃料消耗率；Fij表示车辆经过路径(i,j)的燃料消耗量。因此，根据碳排放量与燃料消耗量之间的关系，车辆的碳排放量计算方法如下：

Eij=FE·Fij。

(2)

其中，FE表示单位燃料消耗释放的碳排放量。

1.4 多目标MDVRP模型

根据上述符号定义和碳排放量计算方法，最小化物流成本和行驶距离的MDVRP模型如下：

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

fijk≤(Qk-qi)xijk，∀i∈N,∀j∈D,∀k∈K；

(14)

xijk∈{0,1}。

(15)

其中：目标函数(3)表示最小物流配送成本，包括固定成本、燃料消耗成本、碳排放成本3个部分；目标函数(4)表示最小化总行驶距离；式(5)和(6)表示1辆车1次只能服务1个煤炭消耗点；式(7)保证车辆行驶的连续性，即服务完消耗点i之后才能为消耗点j提供服务；式(8)和(9)分别表示车辆的容量约束和行驶里程约束；式(10)和(11)表示车辆的可用性限制，即确定车辆k是否被使用；式(12)至(14)表示车辆行驶在边(i,j)上的载重量限制；式(15)表示0～1变量xijk，当车辆k行驶在路径(i,j)上时xijk=1，否则为0。

2 算法设计

VRP是一类典型的NP-hard问题，国内外学者通常采用启发式或亚启发式算法进行求解[9-13]。MDVRP具有多个配送中心，具有更高的复杂性，且本文提出的问题具有多目标特征，因此，也为NP-hard问题。LAM and LI[14]受到化学反应中分子之间相互作用以寻求势能面中最低势能的启发，提出了化学反应优化算法(chemical reaction optimization,CRO)，已经成为求解组合优化问题的重要方法。

CRO模拟化学反应中分子碰撞以求达到稳定状态的特性，即分子势能达到最低。具体来说，化学反应中的分子经历4个反应，分别为单分子无效碰撞、分解反应、分子间无效撞击以及分子合成反应，且在反应前后遵循能量守恒定律。本文针对所提出的问题特点，采用矩阵编码法和两部编码法两种编码方式，设计了基于贪婪搜索策略的种群初始化方法，进一步设计了4种化学反应。所提出的算法设计如下：

2.1 解的表达

2.1.1两部编码法

两部编码法中，每个解的编码由两部分组成，其结构为：配送车辆服务的消费者数量+消费者服务顺序序列。如图1所示，仓库1中的配送车辆2服务4个消费者，其服务的顺序为2→5→8→3；车辆的行驶路线为：仓库1→2→5→8→3→仓库1，即来自仓库1中的2号配送车从仓库出发，依次服务完消费者2、5、8、3,最终回到仓库1。

图1 两部编码示意图Fig.1 Schematic diagram of two encodings

2.1.2矩阵编码法

矩阵编码法采用矩阵的形式进行编码。首先将MDVRP转化为多个VRP，然后分配车辆，设计行驶路线。如图2所示，仓库1和仓库2各有2辆配送车，每辆配送车在满足容量和行驶里程约束的情况下执行配送任务。如仓库1中的配送车辆1为消耗点4、7提供配送服务，配送路线为：仓库1→4→7→仓库1。

2.2 算法步骤

2.2.1初始化阶段

初始化阶段主要分为两步：算法参数的初始化及种群个体的初始化。

步骤1算法参数的初始化。关于CRO的参数符号、具体意义以及本文中采用的数值如表1所示。

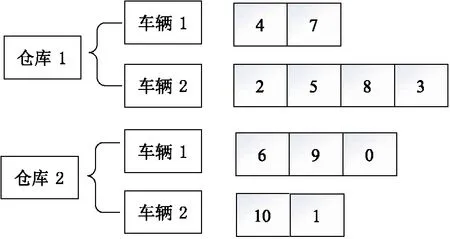
图2 矩阵制编码示意图Fig.2 Schematic diagram of matrix coding

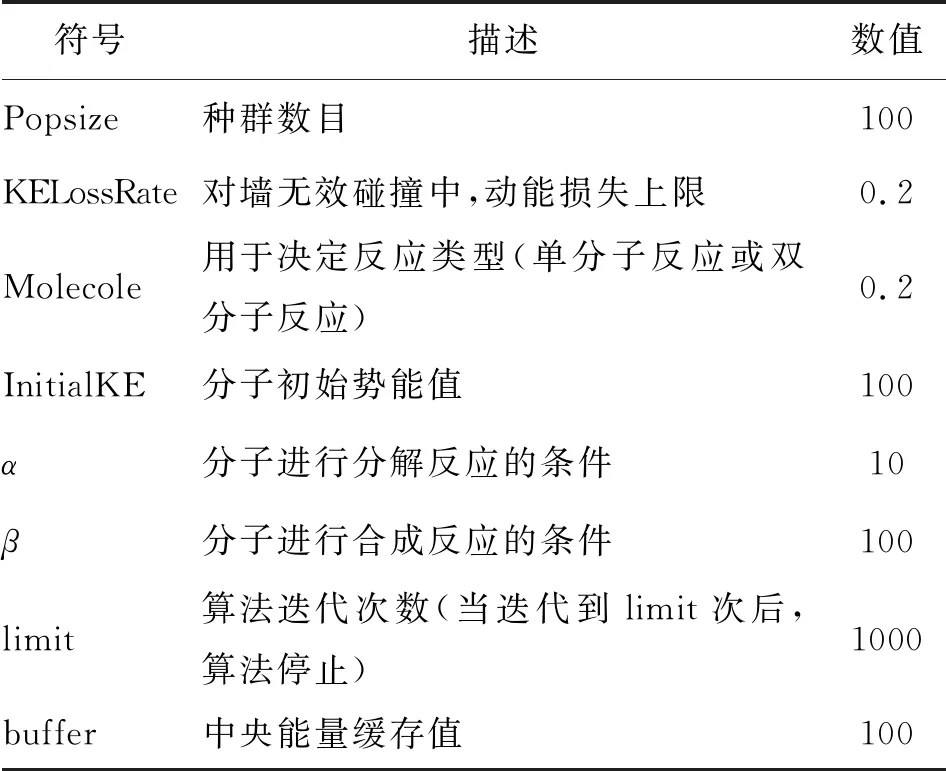
表1 化学反应算法的参数设置Tab.1 Parameter setting of chemical reaction algorithm

步骤2种群的初始化。为了提高解的质量，减少求解时间，以贪婪搜索策略初始化种群个体。首先，根据各个煤炭消耗点与各配送中心的距离分配消耗点到最近的配送中心；其次，按照扫描法对配送中心的消耗点安排配送车辆；最后，调整每辆车所服务的煤炭消耗点先后顺序。

2.2.2单分子无效碰撞

单分子无效碰撞是指单个分子撞击容器壁而得到一个新分子的过程，即ω→ω′。反应后，一部分的分子势能将传递到中央能量缓冲器中。求解本文模型时，单分子无效碰撞采用随机插入算子。具体来说，随机选中一个个体基因，将该基因从基因序列中删除，然后随机将该基因插入到其他位置。如设基因序列为：1|4|7|2|5|8|3|6|9|，选中基因2，在原基因序列中删除该个体基因，得到1|4|7|5|8|3|6|9|，然后将其插入到另一位置。假设插入到基因3之前，那么得到新的基因序列为：1|4|7|5|8|2|3|6|9|。

2.2.3分解反应

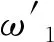
2.2.4分子间无效撞击

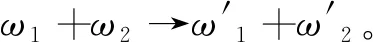
2.2.5分子合成反应

与化学反应中的合成反应类似，化学反应优化算法中多个分子合成一个新的分子(为了简化，这里假设两个分子合成一个分子)，即有：ω1+ω2→ω′。显然，通过允许两分子ω1和ω2合成一个分子ω′的形式，使得新分子ω′在分子结构上与两个分子ω1和ω2形成了较大的差别，继而能够使新分子“探索”一个新的搜索区域，避免陷入局部最优。本文采用最优成本交叉(best cost crossover)反应算子。具体来说，随机从父代1和父代2中选择一个基因，在父代2中删除选中的父代1的基因，然后将父代1中选中的基因插入到父代2中，其中插入位置为能够使得父代2的势能值降低最多的位置，得到子代1。类似地，可得到子代2。最后从两个子代中随机选择一个较优的子代作为ω′。

3 实例分析

本部分随机选取初始化数据进行数值实验。假设有4个配送中心，每个配送中心均有2辆配送车，每辆车的最大载重量和最大行驶距离分别为120 kg和400 km，48个客户的位置在[-50,50]区间内随机产生，消耗点的需求量在[5,25]内随机产生。配送中心和客户信息分别如表2、表3所示：

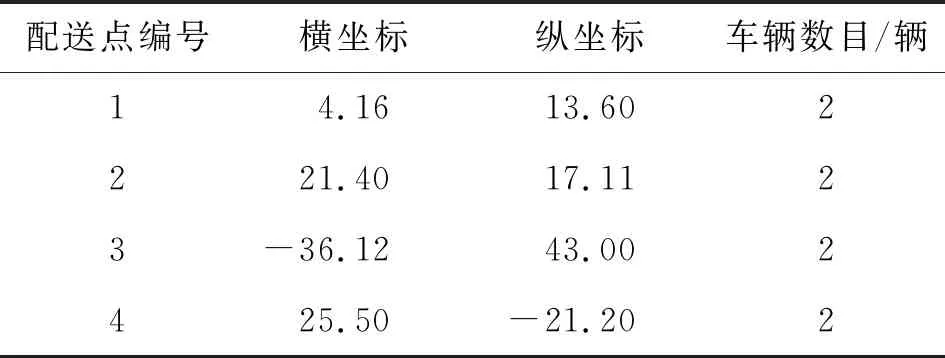
表2 配送中心信息Tab.2 Distribution center information

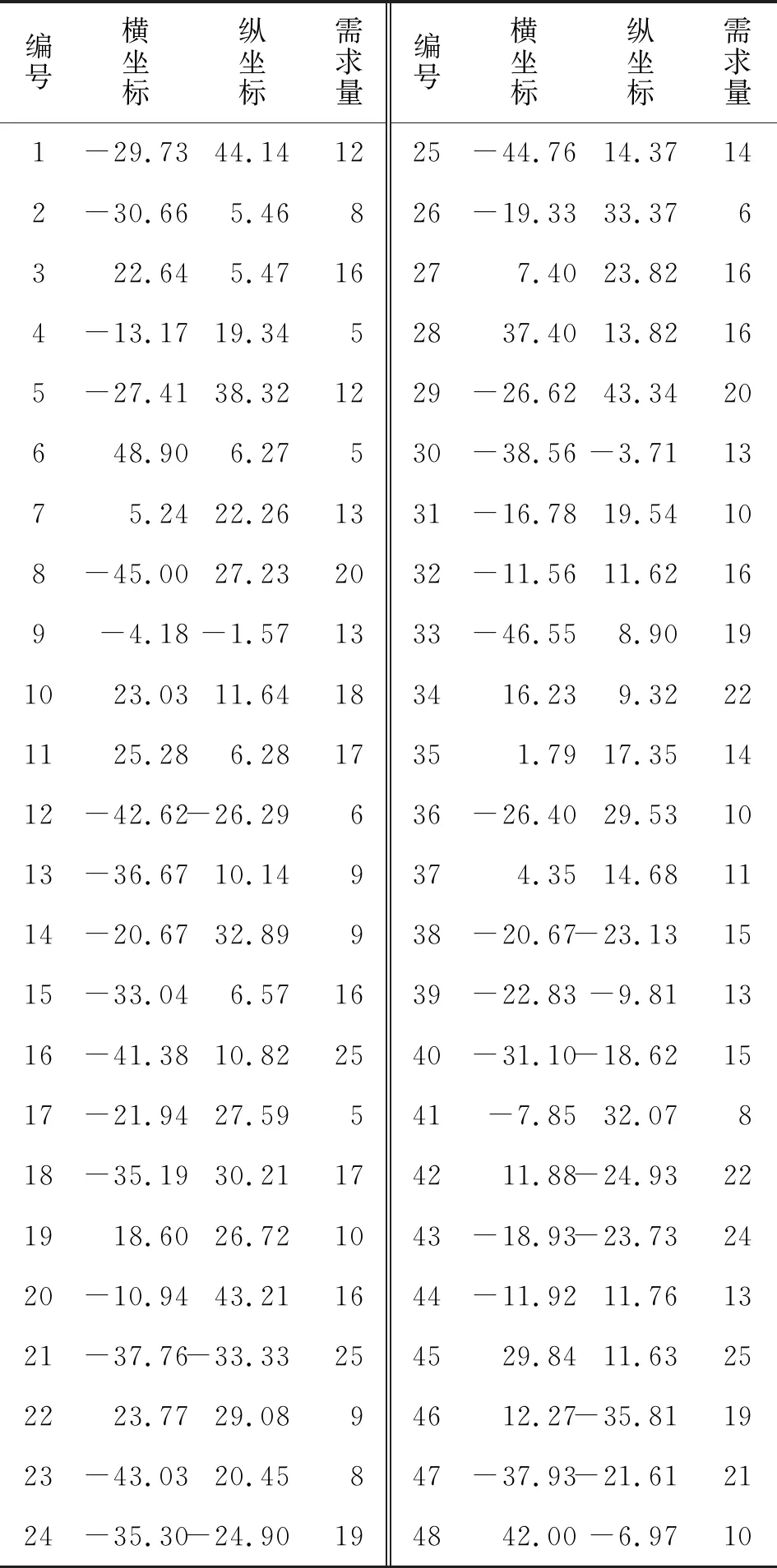
表3 消耗点信息(需求量/kg)Tab.3 Consumption point information (quantity demanded kg)

根据SUZUKI[6]，令ρ0=1，ρ*=2；同时，FACTS E[15]通过研究指出每升燃料消耗释放2.32 kg的碳排放量，单位碳排放成本为2元，配送车辆每天的固定成本为500元，车辆配送中单位变动成本为7.56元。

3.1 物流成本目标求解结果

为了验证贪婪搜索策略的有效性，并对比两种编码方式的优劣，基于化学反应算法的基本框架，本文采用3种求解算法求解模型。

表4 3种算法的详细信息Tab.4 Details of the three algorithms

如表4所示，在编码方式上，算法CRO1采用两部编码法，算法CRO2和算法ICRO(improve chemical reaction optimization)采用矩阵编码法；初始化阶段，ICRO采用2.2.1提出的贪婪搜索策略，而CRO1和CRO2均采用随机初始化方式。考虑到元启发式算法在寻优过程中具有一定的随机性，每个算法各运行10次，将求解结果和CPU耗时汇总在表5中。

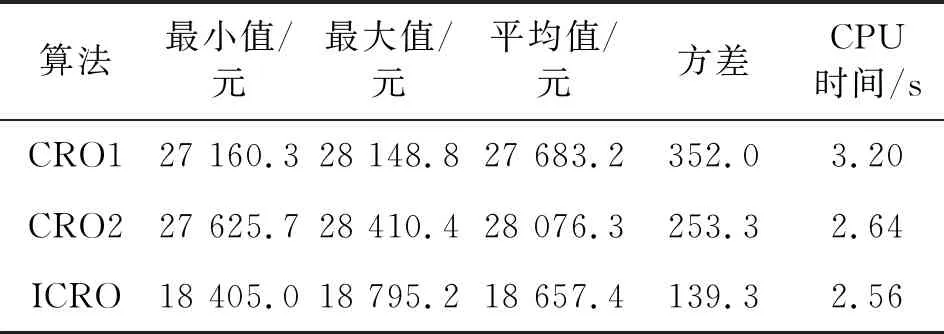
表5 3种算法得到的求解结果对比Tab.5 Comparison of solution results obtained by the three algorithms

由表5可以得到，CRO1和CRO2求解结果相差不大，CRO2求解均值比CRO1降低了1.4%，而CPU时间降低了17.5%。这可能是因为两部编码法需要在求解过程中对行驶路线进行分割而得到每辆车的行驶路线，而矩阵编码方式在初始化阶段就将多配送站转化为单配送站进行求解，降低了问题求解规模，并且MDVRP经过转化后得到的多个VRP问题能够实现并行求解，节省了求解时间。

ICRO算法相比前两种求解方法，在最小值、最大值、平均值、方差以及CPU时间5个维度上均表现出了优势。其中平均值分别提高了32.6%和33.5%。出现较大差距的原因在于CRO1和CRO2均采用随机初始化，车辆使用数为8辆。而ICRO算法在初始化阶段按照车辆的实际载荷以及消耗点与配送站的距离安排车辆，在这种方式下，ICRO算法得到的求解结果中，仅使用了7辆车就完成了配送服务，这样就减少了1辆配送车的成本支出。显然，这对于物流公司来说意味着可以通过合理地设置配送中心的位置，实现成本费用的节省。另外，可以看到，在CPU时间上3个算法求解结果依次递减，也说明贪婪搜索策略相比随机初始化的求解效率高。最后，从10次求解结果的标准差也可以发现，ICRO算法相对来说比较稳定，鲁棒性较好。

3.2 两种优化目标求解结果对比

由3.1可知，ICRO算法相比前两种算法，减少了1辆配送车的成本开支，而配送48个消费者至少需要7辆车才能完成配送任务。另外，注意到碳排放量和燃料消耗量存在一定的比例关系，燃料消耗量的减少也必然使得碳排放减少，故令目标函数(3)中的参数Cf=0,φ=0,Cv=1，分别以最小燃料消耗和最短行驶里程为优化目标，以探讨配送路线数目一定的基础上最小燃料消耗和最短行驶里程两种目标的差异。同样地，为了避免算法的随机性，算法各运行10次(记最小燃料消耗为F′；最短行驶里程为d)，最终求解结果如表6所示。

表6中的第二行、第三行为以最小燃料消耗为目标计算得到的燃料消耗量和行驶里程；类似地，第四行和第五行则为以最短行驶里程为目标得到的燃料消耗量和行驶里程；燃料消耗量偏差值和行驶里程偏差值分别定义如下：

SF′=F′*-Fd；

Sd=dF′-d*。

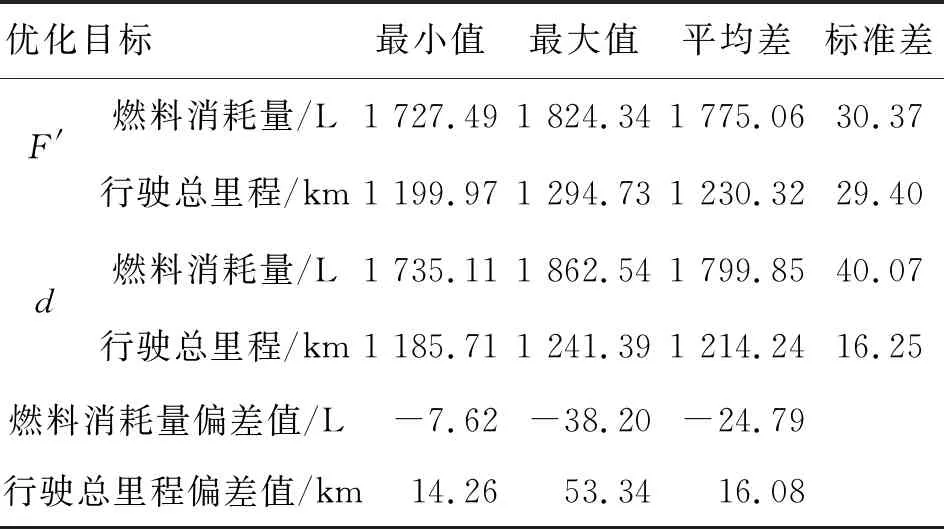
表6 两种优化目标下的求解结果Tab.6 Results of the two optimization objectives

由表6可以看到，当初始目标设定为最小燃料消耗，10次运行结果的最小值为1 727.49 L；而在最小行驶里程目标下，燃料消耗量最小则为1 735.11 L；二者的燃料消耗量偏差值为7.62 L；平均值和最大值分别增加了24.79 L和38.20 L；可以发现每增加14.26 km的行驶里程，就可以节省燃料消耗7.62 L；理论上多行驶53.34 km的里程，可以减少2.20%的燃料消耗量。尽管降低幅度有限，但对大型物流配送企业来说，可以节约巨大的物流成本。而且，从环境保护的角度分析，例如燃料消耗大国美国每年的燃料消耗360亿 L，按照碳排放2.32 kg/ L计算，节省2.20%的燃料消耗将降低18.37亿kg碳排放量。

4 结论

本文在低碳物流快速发展的背景下，充分考虑燃料消耗和碳排放量，构建多目标MDVRP模型，并采用改进后的化学反应算法对问题模型进行求解，完成了以下工作：

(1)构建了基于行驶路径和实际载重量的燃料消耗模型，并进一步建立了碳排放模型，为煤炭配送过程中燃料成本、碳排放量的计算以及燃料消耗成本的优化设计提供了工具。

(2)对比分析了两种优化目标下的燃料消耗量和行驶里程。研究结果表明：可以多行驶一定的路径而降低燃料的使用，为降低燃料成本和低碳物流配送规划问题提供方法指导。

(3)构建了多配送站的物流配送路径规划模型，应用两部编码和矩阵编码两种编码方式，设计了贪婪搜索策略初始化种群个体，并进一步地设计了4种化学反应算法，为求解MDVRP等NP-hard问题提供了参考。