一种改进的K-Prototypes聚类算法

孙志冉，苏 航，梁 毅

北京工业大学 信息学部，北京 100124

1 引言

聚类算法[1]作为数据挖掘领域的重要组成部分，能够在无标记样本的条件下，根据各数据对象的相关信息，将相似的对象进行分类，使得同一类中的对象尽可能相似，不同类中的对象差异尽可能大，从而发现数据的潜在结构和组织规律。在现实的应用中，数据集中不仅包含着年龄、身高等定量的数值属性，还包含如性别、职业等类别属性，同时包含数值型属性和类别型属性的混合型数据集无处不在。为解决混合型数据的聚类问题，Huang 提出了由K-Means[2]和K-Modes[3]算法结合而成的，可处理混合型数据的K-Prototypes[3]聚类算法。该算法具备简单高效的特点，应用也十分广泛，但是仍然存在不足，如随机选择初始聚类中心导致算法稳定性和准确率较差、需要人为确定类簇个数等。

针对原始K-Prototypes 算法的问题，近年来有不少学者进行了不同程度的优化。针对属性值距离度量表示不准确的问题，陈韡等[4]改进了分类属性的距离计算公式，不单单考虑样本与聚类中心的距离，还加入了样本与类簇中已有数据之间的差异；Sangam等[5]考虑每个类别的相对频率和分布，对分类属性采用加权汉明距离测度；Cui等[6]提出了RS-K-Prototypes算法，将数值数据离散化为分类数据，利用粗糙集刻画属性值之间的距离，并进行异常值检查，但如果不同类的属性值数据范围之间存在交叉，则离散化数据难以准确分类，聚类结果很大程度上受离散化情况的影响。针对类簇边界数据对象归属应具有模糊性，而在划分迭代过程中没有考虑模糊性的问题，Chen等[7]考虑到样本在类簇归属上的模糊性，根据模糊隶属度的思想，提出了模糊K-Prototypes（FuzzyK-Prototypes，FKP）算法。针对忽视了各属性对聚类结果的贡献可能不同的问题，Ji等提出了IWKM算法和WFK-Prototypes 算法[8]，利用模糊集和模糊质心的思想，考虑了不同属性对聚类过程的不同影响力，在一定程度上提高了聚类精度；欧阳浩等人[9]根据信息熵对分类属性赋权值，并利用粗糙集表示对象之间的差异度；Yao 等[10]提出了基于K-Prototypes 的 KLS 算法，改进了距离算法的距离公式，对数值型和分类型属性的权重进行了统一，可以满足敏感属性的多级隐私保护要求，但该算法的权重是由专家预先指定，需要大量人工干预。为改进传统算法随机选择初始中心点的问题，Zheng 等[11]提出了进化K-Prototypes（EvolutionaryKPrototypes，EKP）算法，引入了具有全局搜索能力的进化算法（Evolutionary Algorithm，EA），改进了K-Prototypes聚类结果对初始选点敏感，容易造成局部最优的问题，但未对距离计算方式改进，所以结果仍不太理想；文献[12]基于先验信息利用最大最小距离算法确定类簇个数和初始中心，但该算法需要有类标签信息；文献[13-15]都能够根据密度和距离分布[16]选择初始聚类中心，但DC-MDACC 算法[13]中心点受置信因子参数影响较大，DPCM[14]算法利用拐点进行选择，对于多个类簇的识别，效果不佳，DP-MD-FN 算法[15]引入了额外的阈值截断参数来选择中心点，参数需先验知识，且可能选出同一类簇的两个高密度点，造成聚类结果有误。

以上算法从不同方面改进了原算法的不足，但鲜少有能自动确定类簇个数的改进方法，且大多算法初始选点随机具有不稳定性。为解决该问题，本文提出基于密度自动确定聚类中心的DACKP 算法，该算法根据数据对象的密度和数据对象间的距离，实现类簇个数的自动识别，并选择出初始聚类中心，优化初始选点造成的局部最优问题，保证聚类结果的准确性。另外，在聚类过程中还优化了距离公式，考虑各属性对聚类的不同影响，并保存类簇中重要属性值，以达到更好的聚类效果。

2 传统K-Prototypes聚类算法

K-Prototypes 聚类算法是对K-Means 和K-Modes 聚类算法的扩展，用于处理混合型数据的聚类问题。

定义1设S=(U,A,V,f)是一个信息系统，其中U={x1,x2,…,xn}是由n(n≥1)个数据对象组成的有限数据集合，xi(1 ≤i≤n)表示由m(m≥1)个属性描述的数据对象；A={a1,a2,…,amr,amr+1,amr+2,…,amr+mc}表示m个属性组成的有限属性集合，其中a1～amr表示mr个数值型属性，amr+1～amr+mc表示mc个分类型属性，即m=mr+mc；V={vj|1 ≤j≤m}表示所有属性值域的集合，vj表示属性aj的取值集合，aj∈A，若1 ≤j≤mr，则vj由实数域表示数值属性取值集合，根据实际需求确定上下界，若mr＜j≤m，则vj={v1j,v2j,…,vnjj}表示分类属性取值集合，nj表示分类属性aj的不同取值个数；f:U×A→V表示一个数据对象的映射信息函数，对∀xi∈U,aj∈A，有f(xi,aj)∈vj。

定义2数据集U聚类过程中的类簇划分表示为集合C={C1,C2,…,Ck}，其中k为类簇个数，U，并且Ci⋂Cj=∅(1 ≤i,j≤k,i≠j)，即C是U的一个划分。

定义3属性值在类簇Cl中的出现比例表示为并且0 ≤。

定义4数据集U聚类过程中类簇的中心点表示为集合Z={z1,z2,…,zk}，zl表示类簇Cl的中心点，且对每个中心点zl(1 ≤l≤k)都有：

数据对象xi和类中心zl的相异度为：

K-Prototypes算法的目标函数可描述为：

其中，wli∈{0,1} ，1表示数据对象xi被划分到第l个类簇中，0 表示数据对象xi没有被划分到第l个类簇中，每个数据对象被划分且仅被划分到一个类簇中。

K-Prototypes 算法的步骤为：输入为数据集U和类簇个数k；首先从数据集中随机选择k个样本作为初始聚类中心Z；然后根据相异度度量公式（2）把数据集中的样本x逐一分配到最近的类簇中，并按照公式（1）更新聚类中心Z，迭代划分和更新聚类中心的过程，直到目标函数F不再发生变化，即每个数据对象不再改变所属聚类时算法结束，得到聚类结果C。

K-Prototypes 聚类算法达到迭代终止条件，即目标函数F减小到不再变化时，则认为算法收敛，但目标函数可能有多个极值点，而初始聚类中心的选择，可能导致算法收敛到局部最优，所以K-Prototypes 聚类算法对初始聚类中心敏感。另外算法采用公式（2）来度量数据对象间的相异度，忽略了数值属性对聚类结果的影响，以及不同属性对聚类结果的不同影响；由于分类属性聚类中心单值表示的问题，造成属性缺失，不能准确刻画类簇的信息，造成分类属性的相异度度量忽略了类内对象的总体相异度，并且当相异度相同时，算法不能准确地划分到相似性更大的类簇中。K-Prototypes 算法还需指定类簇数目，而对于无序的数据集，类簇数目往往很难确定。针对上述问题，本文提出了一种改进K-Prototypes算法。

3 改进的K-Prototypes算法

针对K-Prototypes 算法的不足，本文提出了新的相异度度量方法，并解决随机选取初始聚类中心的问题，且可自动确定类簇数目，提高算法的准确率和稳定性。

3.1 新相异度度量公式

本文提出的相异度度量方法，使用信息熵来确定各属性的重要程度，对各属性进行加权；对于分类属性相异度度量采用多Modes的聚类中心，不单单保留类簇内出现频率最高的值，而是保留全部属性值及其出现频率，并给出混合属性的相异度度量公式。

信息熵表示事件发生的概率，对于数值属性aj(1 ≤表示在属性aj下对象xi的取值所占的比重；对于分类属性aj(mr＜j≤m) ，表示在属性aj下第t个属性值所占的比重，其中ntj表示属性值为的对象个数，故各属性的信息熵表示为：

属性在聚类过程中的重要程度与其属性值构成的差异度成正比。熵值越大则属性值差异度越大，故该属性的权重值应该更高，反之，熵值越小表明属性值差异度越小，故该属性的权重值应该更低。属性aj权重值表示为0 ≤ωj≤ 1 。

根据定义4可知，传统算法对分类属性聚类中心的表示是直接选择频率最高的属性值，这不能准确地刻画类簇内的信息，在多于一个类簇出现频率最高的属性值相同时，数据对象到每个类簇的距离相同，算法不能准确划分到更相近的类簇中，故本文将聚类中心的分类属性值表示为该属性的所有属性值及其出现频率组合，则聚类中心的映射函数定义为：

基于权重和聚类中心的优化，本文给出的相异度度量公式定义为：

3.2 初始聚类中心点的选取

为解决随机或人工干预选择聚类中心的问题，考虑到数据的实际分布情况，结合文献[16]提出的数据分布的密度和高密度距离定义，本文使其应用到混合数据集上，并提出了初始聚类中心点的选取方法，能够有效地确定初始中心点和类簇个数。该方法首先进行聚类中心的预选取，然后进行优化确认最终的中心点集合和类簇个数。

（1）聚类中心预选取：通常情况下，中心点往往分布在数据对象密度较高的区域中，且不同类簇之间的间距较大，根据这两个假设，文献[16]定义两个关键参数：①每个数据对象xi的局部密度ρi，常用截断核和高斯核两种定义方式，分别如公式（7）和（8）所示，公式（7）取值为离散的整数，往往用于大规模数据集，公式（8）取值为实数；②每个数据对象xi到局部密度高于它且距离最近的数据点xj之间的距离δi，定义如公式（9）：

其中，d(xi,xj)表示数据对象xi和xj之间的距离，dl为截断距离，由近邻占比pd来确定，通常pd∈[1%，2%]，即所有d(xi,xj)由小到大排序后第1%到2%的值取作dl；为了能更好适用于混合数据集，结合3.1节中提出相异度度量公式，数据对象之间的距离公式描述为：

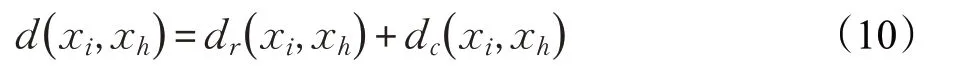
其中：

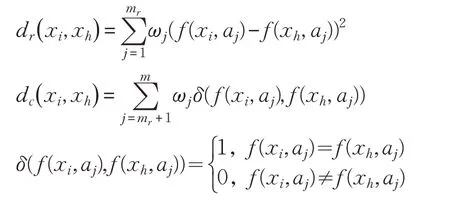
由于聚类中心的局部密度应该大于其周围数据对象的局部密度，且不同类簇的聚类中心之间的距离应该相对较远，故聚类中心点应为ρi和δi都较高的数据点，则设定预选初始中心点集合Zp应满足：

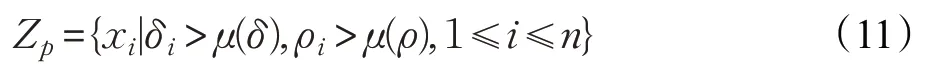
其中，μ(δ)表示所有数据对象δi的均值，μ(ρ)表示ρi的均值。通过均值筛选掉大部分单个类簇中的多余密度较大的点，以及δi值过大但密度较小的噪声点。

（2）聚类中心优化：预选中心点集合中包含了实际应有的中心点，但也包含了非中心点（高密度类簇内，中心点附近往往存在密度同样较大的点），如图1所示，多余的中心点导致红色框内的原本一个类簇，分为了两个类簇。为防止这种情况，需要将原本属于一个类簇的预选中心点进行合并，如图2 所示，两个中心点之间的距离应为大于2dl，若小于2dl，则表示两个中心点属于同一个类簇。

图1 R15数据集上的错误聚类结果

图2 中心点距离决策图

最终中心点选取过程：首先对Zp集合中的数据根据公式（12）计算ηi，ηi综合考虑了ρi和δi，且忽略了量纲的差异，ηi值越大越可能成为中心点。

然后将数据对象按照ηi从大到小排序，选ηi最大的数据对象作为确认的中心点，添加到最终的初始中心点集合Z0中；其余预选中心点按照排序后的顺序，依次计算与排序在它之前的数据对象之间的距离，若皆大于2dl则表示该对象可作为初始中心点，将xi添加入Z0中，初始中心点集合Z0表示为：

最终将集合Z0中元素作为初始中心点，集合Z0大小作为类簇个数。

3.3 DACKP算法

改进后的DACKP 算法主要包括聚类中心点预选取，确定中心点和迭代聚类划分过程3 个步骤，基本步骤描述如下：

输入：数据集U和近邻占比pd

输出：聚类划分结果C

步骤1根据公式（10）计算任意两个数据对象之间的距离d(xi,xj),1 ≤i,j≤n。

步骤2根据pd，确定截断距离dl，根据公式（8）对每个数据对象xi计算其局部密度ρi。

步骤3根据公式（9）对每个数据对象xi计算其高密度距离δi。

步骤4计算δi和ρi的均值μ(δ)和μ(ρ)，并根据公式（11）得到预选初始中心点集合Zp。

步骤5对 ∀xi∈Zp，根据公式（12）计算其ηi值，并进行由大到小排序。

步骤6根据公式（13）确定最终初始中心点集合Z0。

步骤7使用相异度度量公式（6）计算每个数据点到各个聚类中心之间的相异度，并把数据集中的样本逐一分配到最近的类簇中。

步骤8更新聚类中心Z，数值型属性类中心为该类簇中所有该属性值的平均值，分类型属性类中心为类簇中该属性各属性值及其出现的频率。

步骤9重复上述步骤7 和步骤9 的过程，直到目标函数F不再发生变化，即每个数据对象不再改变所属聚类时算法结束。

通过分析可知，传统K-Prototypes 算法的时间复杂度为O(nkT)，其中n表示数据对象个数，k表示类簇个数，T表示迭代次数；本文算法的主要计算开销有：中心点选取的时间复杂度为O(n2)、迭代计算的时间复杂度为O(nkT′)，一般情况下k∈[2,n][17]，T′为改进后算法的迭代次数，根据实验结果，准确的聚类中心使其值较小T′≪n，所以本文算法的时间复杂度为O(n2)。中心点的选取虽然耗时较多，提高了算法的复杂度，但避免了盲目的随机选点，提高聚类的有效性。

4 实验结果

为验证本文提出的算法的有效性，本文使用了人工合成数据集和UCI 机器学习库中的数据集进行验证，如表1 所示，本文分别选取了数值属性数据集、分类属性数据集和混合属性数据集。并根据数据集类型，将DACKP 算法分别和K-Means 算法、DPC 算法[16]、FuzzyK-Means（FCM）算法、K-Modes 算法、K-Prototypes（KP）算法、DPCM算法、FuzzyK-Prototypes（FKP）算法进行比较。实验环境为Intel®Core™ i7-4790K CPU @ 4.00 GHz，16 GB内存，操作系统为Microsoft Windows 10。

表1 验证数据集描述

为了评估聚类算法效果，本文采用的评价指标包括正确率（AC）、类精度（PE）、召回率（RE）和执行划分步骤的迭代次数（Iter），评价指标定义如下：

其中，n表示的是数据集中对象的总个数，ni表示的是被正确分配到第i个类簇的对象个数，cni表示的是聚类结果中第i个类簇的对象个数，pni表示的是真实标签中第i个类簇的对象个数。

在对比实验中，对于随机初始选点的K-Means、FCM、K-Modes、KP 和FKP 算法，给出正确的聚类个数参数，并采用了100次随机初始选点，最终统计平均值；KP算法的重要参数γ=分类属性个数/数值属性个数[9]；DPCM算法依照原文参数pd=1.5%，给出正确聚类个数，选择η值最大的数据对象作为初始中心点；DPC和本文算法同样取pd=1.5%。

数据集R15和D31为人工合成的二维数据集，其聚类结果如图3、图4所示，不同颜色代表不同类簇，“*”表示初始中心点。可直观看出，本文算法可准确地识别出类簇数和初始中心，得到正确的聚类结果。

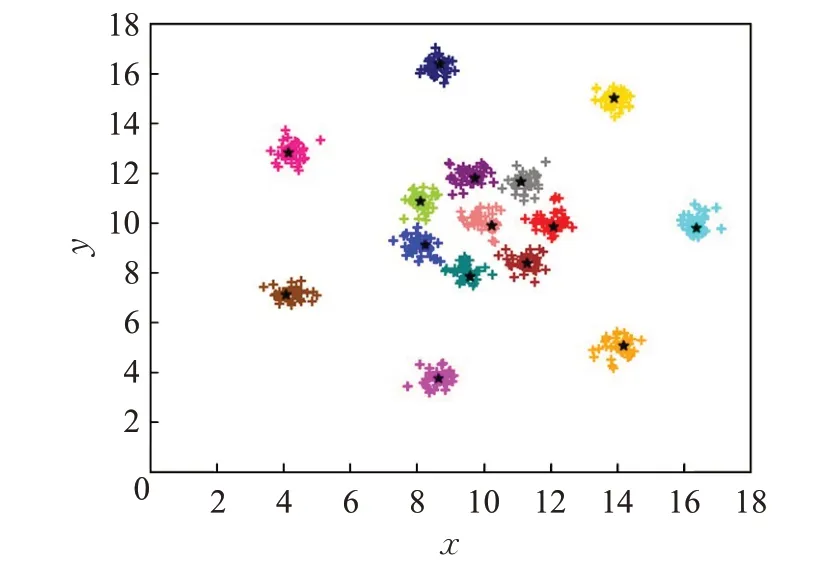
图3 本文算法在R15数据集上的聚类结果

图4 本文算法在D31数据集上的聚类结果

如表2 给出的各算法在数值属性和分类数据集上的评价结果，对于数值属性数据集，K-Means 算法对初始选点敏感、DPC 算法对参数也有依赖性，得到的结果并不能代表其最佳水平，FCM算法引入模糊理论，其结果普遍优于K-means 和DPC 算法。本文算法相较K-Means和DPC表现较好，准确率上和FCM几乎持平，但本文算法迭代次数有明显的优势，收敛速度更优。在分类数据集上的实验结果，本文算法因改进了分类属性相异度表示和稳定了中心点的选取，达到了良好的聚类效果。

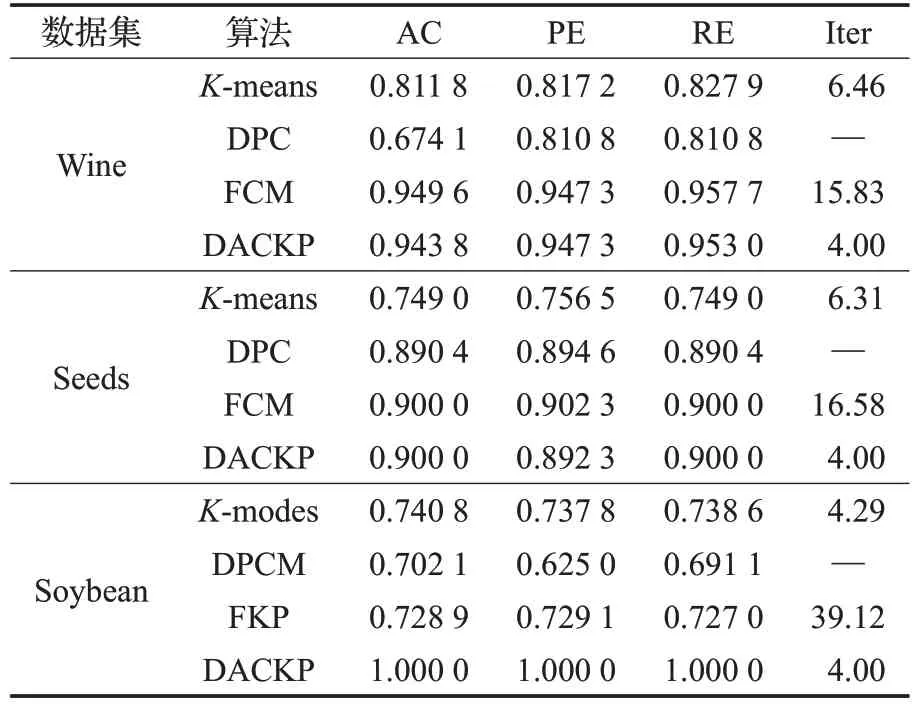
表2 数值属性和分类属性数据集实验结果比较

本文验证混合属性数据集聚类效果，结果如表3所示。KP 和FKP 因中心点选择不稳定，相似度度量方法过于粗糙，导致在各数据集效果皆不佳；DPCM 算法对于非高密度的点会因一个数据对象划分错误，造成连锁反应，导致准确率低。本文算法在German Credit Data数据集准确率略差，主要是以为该数据集类簇分布比例差异较大，使用导致初始选点不够准确，但在精准度和召回率上要优于其他算法。在其他数据集上本文算法聚类指标都高于其他算法均能有效的聚类。根据多个混合属性数据集实验结果，与传统KP算法相比，本文算法平均准确率提高了8.52%，与DPCM算法和FKP算法相比，平均准确率分别提高了4.28%和8.33%，且本文算法能保证聚类的稳定性。

表3 混合属性数据集实验结果比较

5 结束语

本文提出的DACKP 算法，结合数据对象的密度分布优化了初始聚类中心的选取问题，且可自动地确定类簇数目，另外通过区分每个属性对聚类结果的不同影响权重，和优化聚类中心的表示方式，改进了相异度计算公式，强化了属性间的差异性和类内相似性。本文使用人工数据集和UCI 数据集进行验证，实验结果表明，改进后的DACKP 算法与其他算法相比，聚类结果的准确率、精准率和召回率都有所提高。但算法对于类簇分布比例差异较大的数据集提升效果并不明显，如何改善此类数据集的聚类效果和提升算法的时间复杂度是下一步的主要工作。