超声驻波场中固液黏附液滴悬浮分离研究

麻寿东，吴立群，郭亚杰，庄 龙，吴 浩

(杭州电子科技大学机械工程学院，浙江杭州310018)

0 引 言

内加工[1-4]直接将加工工具即高能束用于待加工材料内部，改变指定位置处的物理、化学特性，完成材料微观结构改变或性能修饰，实现中空微结构制造。与传统“外加工”方法互补，联合发挥作用，有利于突破传统设计方法和加工工艺的约束，解决制备三维中空微结构时，加工速度慢、处理工序多、产品成功率低及复杂空间型结构不易实现等问题，具有广阔的应用前景。

然而，废屑如何顺利排出是限制内加工技术发展的瓶颈，国内外学者就此做了大量研究。Li等[5]研究了玻璃三维空间螺旋形微通道飞秒激光与材料相互作用机制，探讨了废屑排出对加工质量和效率的影响；Hwang等研究了不同截面形状、深宽比在不同液体辅助下的加工机制，研究了辅助液粘度对排屑的促进作用[6]；Kevin等[7]研究了低功率飞秒激光加工螺旋形通道中排屑的动态过程。通过对文献分析可以得出以下结论：(1)内加工集中在透明材料领域，对金属材料内加工的研究较少；(2)排屑是影响加工质量和效率的关键因素，以往研究多集中在液体辅助排屑等方面，对超声辅助排屑的研究未见系统报道。

基于此，本文致力于研究声悬浮条件下金属材料内加工熔融废料排出过程，且作为前瞻性研究，运用超声技术，将废料排出过程简化成声悬浮条件下，液滴与固体的分离脱附过程。

1 数值方法

1.1 数学建模

声悬浮条件下简化固液脱附模型如图 1(a)所示，平壁上液滴加载超声驻波，液滴在声流耦合作用下，液面收缩，边界分离，进而在驻波节点稳定悬浮(图 1(b)所示)。固液界面润湿角θ如图 1(c)所示，表征固体相界、气体相界、液体相界相互之间的界面张力的关系；设定固液接触面半径为λ。

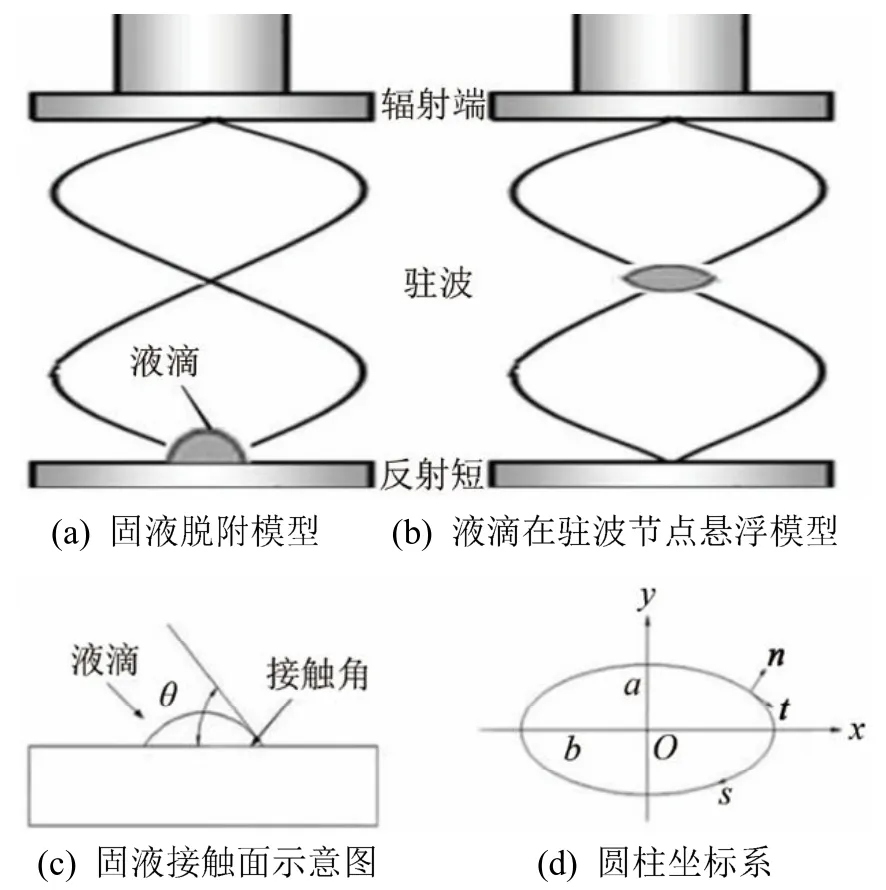
图1 固液脱附模型Fig.1 Solid-liquid desorption model

以辐射端及反射端之间为计算域，建立相关数学模型如下。

(1)连续性方程[8]：

式中：ρm为计算域的平均密度；u为液滴速度；定义液滴与计算域的体积比为β，ρG为计算域中空气密度，ρL为液滴密度，则有

(2)伯努利方程[8]：

式中：M为平均动量，则将式(1)代入式(3)，有：

因u及βu的二次项较小，结合式(2)，上述方程可化为

(3)运动学方程[8]：

考虑液滴的运动速度及运动过程，液滴内部不可压缩，并假设液滴内部是无粘且无旋的，故速度u可描述为势能ΦL的梯度：u =-∇ΦL。液滴内部速度势满足拉普拉斯(Laplace)方程：

液滴表面的运动学条件可由伯努利方程定义：

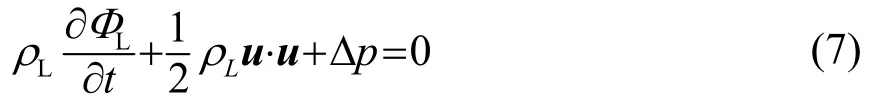
式中：Δp是驱动液滴振动的气液界面压差，与表面张力、静压力、声辐射压力、黏附力相平衡：

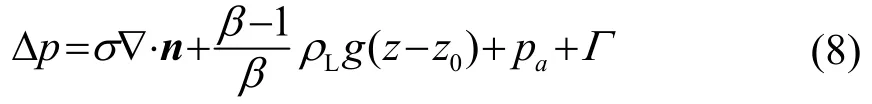
式中：z是垂直方向坐标；z0是液表面垂直方向坐标的最大值；如图1(d)所示，n是曲面的单位外法线向量；t是与之对应的单位外切线向量。因液滴振动频率远低于超声波频率，故作用在液滴表面的声辐射压力可表示为时均声辐射压力：

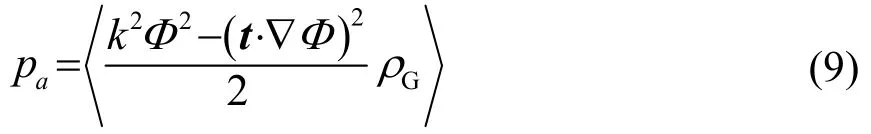
为简化计算，使用圆柱坐标系，如图1(d)所示，s为母线沿液滴表面的弧长。定义特征长度a0为液滴当量球体半径，特征压力p0为半径a0的球体液滴所产生的表面张力，特征速度势Φ0为入射声场速度势幅值，则液滴表面演变的数学描述可表达为入射声场速度场振幅：

至此，可得液滴表面边界积分方程，并采用边界元法求解：

式中：G(r,r′)是在自由空间中声场的格林(Green)函数，Φm=s in[K(z - h)]e xp(- jω t)是入射声场的速度势。

1.2 计算方法

方程(10)～(12)为一阶微分方程，描述了液滴表面随时间推移的运动。假设初始条件液滴表面速度为零，采用四阶Runge-Kutta法数值求解，并记录液滴表面形状及速度。为加快计算进程及稳定性，首先模拟声压分布，并将其作为初始条件，采用两相流-移动网格技术模拟超声驻波作用下液滴形态及运动状态变化。采用多物理场仿真软件 COMSOL Multiphysics进行模拟计算，计算域及边界条件如图2所示，计算参数如表1所示。

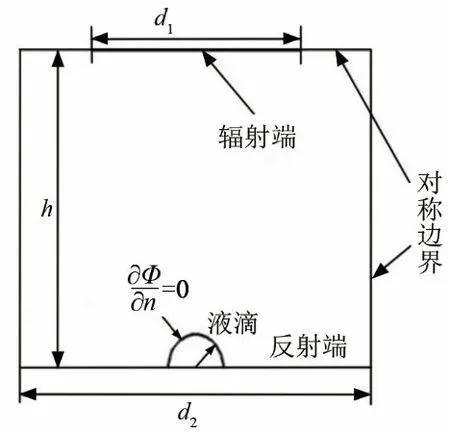
图2 计算域及边界条件Fig.2 Calculation domain and boundary conditions

表1 计算参数Table 1 Calculation parameters

应用三阶B样条差值函数，计算表面张力、压力及流体静压，同时用边界元法求解声散射问题，获得液滴表面声场速度势，进而求得目标函数。

2 试验方法

2.1 试验设备

根据相应简化模型及理论分析，搭建液滴悬浮分离试验台(如图 3所示)，主要设备仪器包括：超声波发生器、辐射端、反射端、CCD、光源及辅助设备如运动控制设备等，相关设备厂家及参数如表2所示。

图3 液滴悬浮分离试验系统图Fig.3 Test system for droplet suspension separation

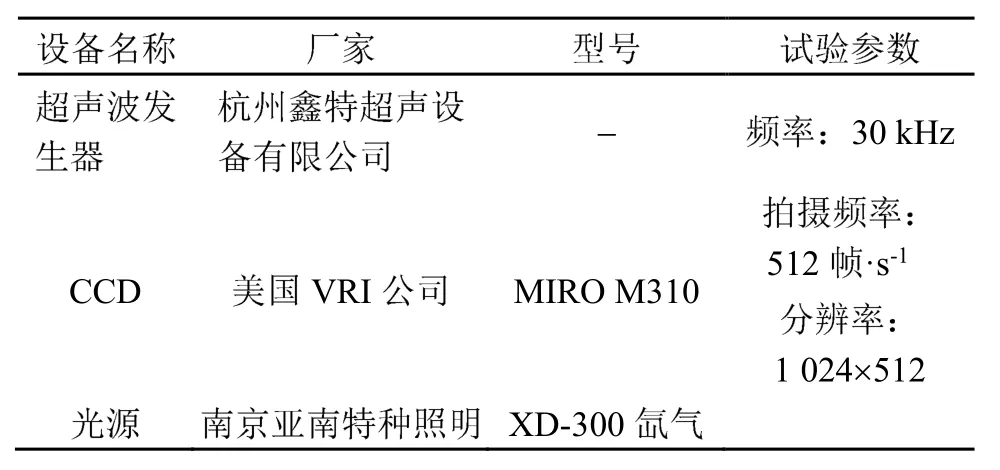
表2 各设备厂家、型号及参数Table 2 Equipment manufacturers,models and parameters

2.2 试验过程

采用拍摄光源照明整个流场及声场，使液滴脱附，并用 CCD拍摄脱附过程。所用光源为白光，拍摄频率为512帧·s-1，分辨率为1 024×512。

3 结果及分析

3.1 驻波场有无液滴声压分布

声压分布如图4所示。图4(a)中无液滴时，声压基本呈轴对称分布，等压面为一系列形状规则的封闭曲面。图4(b)有液滴时，声压虽仍呈轴对称分布，但近反射端和辐射端的声压分布与无液滴时声压分布明显不同，等压面形状发生变化，不具有规则形状，且部分等压面不再完全封闭于计算域内部；整体声压降低，近反射端声压较无液滴状态降低30%；反射端等压面分为左右对称的两个半球，明显不同于图4(a)中无液滴时的等压面。从图4(b)液滴表面A、B、C三处的声压分布可知，A、B两处声压大于液滴内部 C处声压，与文献[8]结论相似。此力学行为可促使液滴收缩分离，为液滴超声悬浮分离的可靠性提供了理论支持。

图4 有液滴和无液滴情况下的总声压场分布仿真结果Fig.4 Simulation of total sound pressure field distribution with(a)and without(b)droplets

3.2 液滴纵轴及横轴声压及流线分布

为讨论液滴纵轴及横轴的声压及流线分布，选取 如 图 4(b)中 一 定 区 域(12≤x≤1 8 mm ，-2≤y≤0 mm)作为研究对象，结果如图5、6所示。

由图5(a)可见，纵轴声辐射压力关于液滴顶点对称分布，声辐射压力随着高度的降低，逐渐减小，并在液面处达到最小值 0.4 kPa；随着液滴深度增加，声辐射压力逐渐增大，但增加速度降低。由图5(b)可知，声辐射压力关于液滴纵轴对称分布，从中心沿径向声辐射压力先呈逐渐减小趋势，直至液滴边缘附近，随后声辐射压力沿径向上升，在这一过程中声压的减小速度及上升速度逐渐增加，且整个声辐射压力曲线呈抛物线形状。

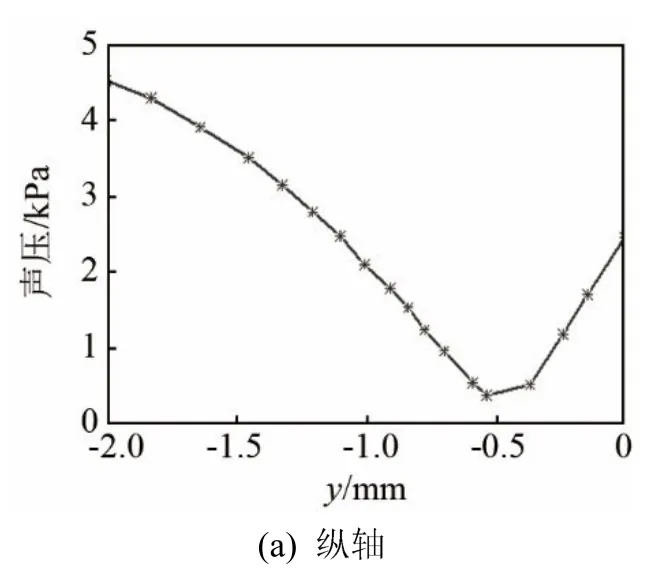
图5 声压沿液滴纵轴及横轴的变化Fig.5 Variations of sound pressure along the longitudinal and transverse direction of the droplet

图6为5 ms和10 ms时液滴纵轴及横轴流线分布。由图6(a)可见，t=5 ms时，液滴在声压的作用下，流线分别在左右两侧呈顺时针和逆时针方向旋转，流体向延展的方向发展；在t=10 ms时，流线分别在左右两侧呈逆时针和顺时针方向，流体从边界流向中心，形成向上流动的趋势。

图6 在5 ms和10 ms时刻的液滴纵轴及横轴流线分布Fig.6 Streamline distributions along longitudinal axis and transverse direction of the droplet at t=5 ms and 10 ms

经分析可知，液滴黏附中心声辐射压力在两个方向上均呈最大值，相当于有一合力促使液滴向上。同时，液滴受径向向内声辐射压力的作用，整个液滴有向上的趋势。

3.3 超声驻波场作用下黏附液滴悬浮分离过程

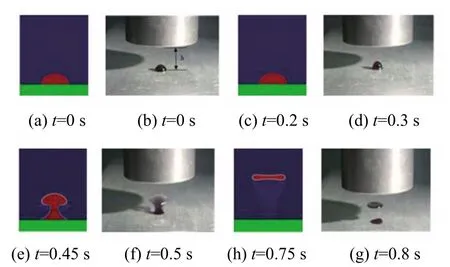
图7 液滴悬浮分离过程Fig.7 Droplet suspension separation process

为准确描述液滴形态变化及运动过程，一个周期(0.8 s)内各态演变数值模拟及试验结果如图 7所示。t=0时，液滴在表面张力及黏附力的作用下附于铝质反射端表面，并在此时施加超声波作用；t=0.2～0.3 s时，液滴在声辐射压力作用下开始收缩变形，润湿角θ逐渐增大，形变明显；t=0.45～0.5 s时，声辐射力、表面张力、黏附力、静压等力耦合作用驱动液滴轴剖面两侧流体向中心集聚，液滴被纵向拉长呈蘑菇状，出现分离趋势；t=0.75～0.8 s时，液滴稳定悬浮在驻波节点，并在声压的作用下发生形变，呈扁球状，进一步被压扁，上下表面中央部位实现由凸面到凹面的转变，与解文军[9]的结论一致；t＞0.8 s，液滴在驻波节点处发生雾化。

4 结 论

通过以上研究，可得如下结论：

(1)液滴剖面两侧处声压大于液滴内部声压，可促使液滴收缩分离；

(2)液滴形变及运动过程表明，在声辐射力、表面张力、黏附力、静压等力耦合作用下，液滴发生变形，驱动液滴轴剖面两侧流体向中心集聚，进而实现分离，并以中央凹陷的扁平球状稳定悬浮在驻波节点处；

(3)改变声压，液滴在驻波节点处发生雾化。