机械腿逆运动学模型求解

胡平志, 李泽滔

(贵州大学 电气工程学院, 贵阳550025)

0 引 言

近年来,越来越多机器人被广泛应用。 轮式机器人不能适应复杂的地形环境,飞行机器人虽然能无视地形因素,但是载重量有限,成本极高。 随着机器人技术的迅猛发展,对能在复杂环境下行走的特种机器人的需求日益增加。 本文以一种十二自由度机器人为研究对象,该机器人实际包含四个三自由度机械腿,其关于机器人几何轴心中心对称式排布。机器人的行走,实际可看作是四条机械腿运动的线性组合,所以为了研究机器人行走,就需要优先研究一条机械腿的模型与控制。

对于单腿建模,学术上通用DH 矩阵法进行建模［1］,该模型被称为运动学正模型,可由每个关节的角度求取末端点的三维空间位置。 但是,实际应用中往往需要利用末端点三维坐标,逆向求取每个关节的角度,这就需要求取运动学逆模型。 然而逆模型方程往往是多元高次方程组,解析解难以求取,甚至不存在。 多自由度机械腿控制,采用建立运动学方程, 由于逆运动学方程中存在交叉项sin (θi) , cos (θi),所以通常是多元高次方程组,解析解求取困难甚至不存在,传统的解决逆问题的办法有两种：(1)利用多特殊点采样,再线性插值拟合的办法；(2)特殊值求解；方法(1)的不足之处在于,进行高精度的线性拟合,需要极大数量的特殊点,由于只能依靠正向模型计算所得的特殊点,其空间位置坐标是随机的,绝大多数点不在期望可行域范围内,不具备实际使用价值。 方法(2)的不足之处在于,所谓特殊值求解,一般而言是将多个关节进行合并,即令θi= C(常数),来对方程进行简化,或者利用机械臂结构上的特殊性进行合并化简［2］,本质上使得高自由度机械腿变为低自由度机械腿。

近年来也出现很多利用智能算法,对逆运动学方程进行求解的论文,这些算法包括,改进粒子群算法［3］,改进神经网络算法［4］等。 但是实际使用中这些算法存在运算量巨大,求解速度慢,求解结果波动范围大的问题。 为更好的解决这一问题,本文提出了一种基于迭代法的方式求解逆模型数值的方法,该方法收敛性好,收敛速度快,准确度高,运算量小,适用范围广。

1 建立坐标系

图1(a)是机械腿的3d 模型,图1(b)是机械腿的3d 模型主视图,红线是转轴与转轴或者转轴与端点之间的垂直距离连线,将这些连线抽象成为连杆,即得到图1(c)。 其中各参数实际取值如表1 所示。

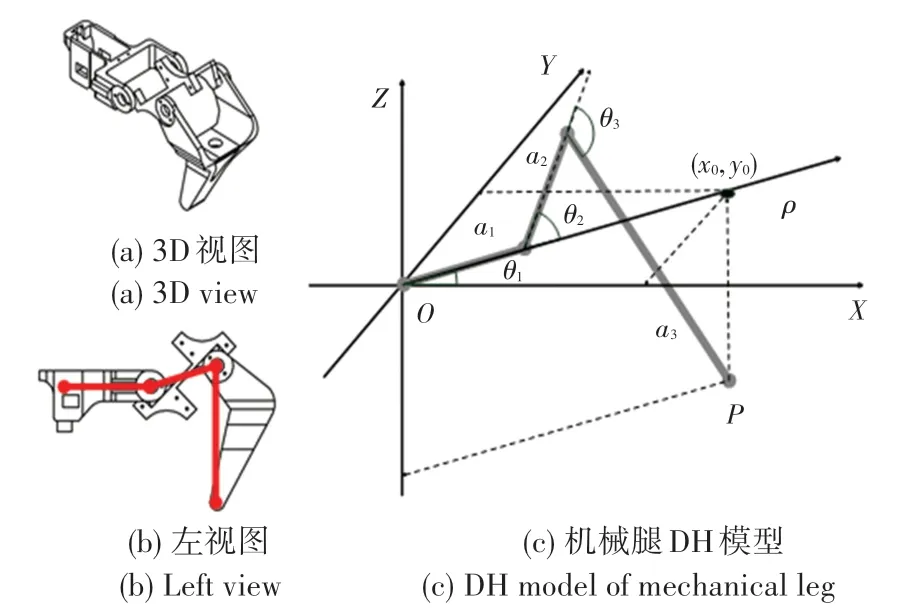
图1 三自由度机器人实物抽象模型Fig. 1 Three-degree-of-freedom-robot-leg model

表1 三自由度机械腿变量声明Tab. 1 Variables of three-degree-of-freedom-robot-leg

对应这一情形,计算化简之后得到方程(1)：

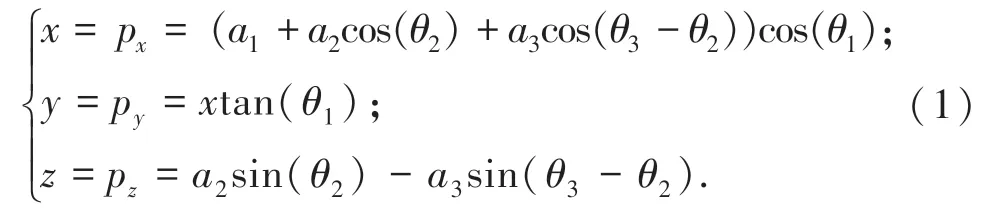
为简化计算,模型方程被转化为圆柱坐标,如图2 所示。

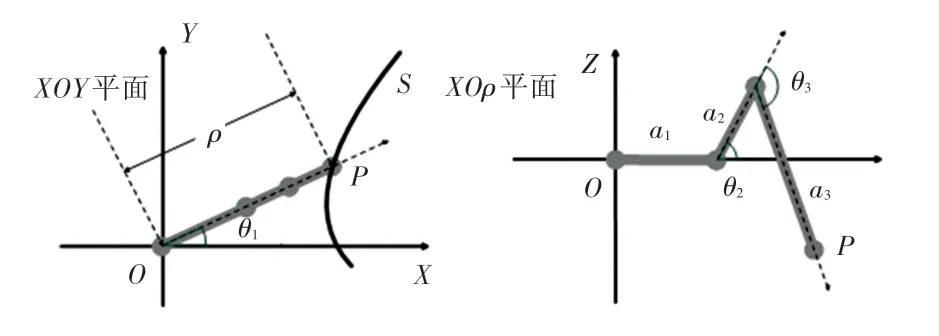
图2 直角坐标变换到柱坐标Fig. 2 Rectangular coordinate to polar coordinate

其中,

2 方程求解

为了控制终端到达任意位置(x0,y0,z0),必须通过该位置求解方程得到各个关节应当输出的角度。 由于不存在解析解,本文提出迭代法进行求解。

2.1 迭代法求解

因为y =f(x),故以下只用讨论x 与z 的关系。

为了让末端点P 沿曲线S 运动,在曲线S 上取得点(x0,y0,z0),求取一组ρ 以及θ1,再在ZOρ 平面上迭代,分别求解出一组θ2、θ3,重复这一过程,即可得到向量组Θi(θ1i,θ2i, θ3i)T,使得末端点P 运动轨迹拟合于曲线S。

为了方便计算,令k =3,利用θ3控制ρ 的变化,并修正由θ2变化带来的偏差Δρ, 由ρ = a1＋a2cos(θ2) ＋a3cos(θ3- θ2) 可以直接分解得

简记为θ3= g(θ2,θ1,ρ)。

利用θ2控制z 的变化,并修正由θ3变化带来的偏差Δz,由z =a2sin(θ2) - a3sin(θ3- θ2) 变换可得到关于sin(θ2) 的一元二次方程,从而可以求解出θ2。

其中该一元二次方程相关参数如式(5)所示。

由一元二次方程求根公式可得求解sin(θ2),利用反三角函数求解出θ2,公式(6)：

θ2表达式简记为：θ2= f(θ3,z),联立式(3) ～ (6) 可得到迭代式(7)：

2.2 迭代收敛证明

该迭代方法敛散性直接影响到是否能得到最后的结果,这里需要证明,随着θ2、θ3的增加(θ2、θ3的初值是其最小值,所以经过迭代只会逐渐增加),P能否从ZOρ 平面上初始位置(ρ*,z*) 收敛到ZOρ平面上目标位置(ρ0,z0)。

因为求解方程z(n)=z0可以得到准确的,但是会使得之前重合的ρ()=ρ0出现新的偏差,即ρ()= ρ0＋Δρ,可以看出,由于系统存在耦合性,每次使得求解z(n)= z0,得到时,都会不断产生偏差Δρ ＞0。 为了使得Δx 绝对值减小,只有在Δρ=ρ() -ρ0是关于的减函数时,迭代才会使得ρ(θ2,θ3) 收敛于ρ0。 由于ρ0为常数,所以求证关于ρ 的迭代收敛,可转换为求证ρ(θ2,θ3) 是关于θ2的减函数。

因为求解方程ρ(n)= ρ0可以得到准确的θ3(n),但是会使得之前重合的z()= z0出现新的偏差,即z() =z0＋Δz,同理每次使得求解ρ(n)= ρ0,得到θ3(n)时,都会不断产生偏差Δz＜0。 为了使得Δz 绝对值减小, 只有在Δz =z() - z0是关于的增函数时,迭代才会使得z(θ2,θ3) 收敛于z0。 由于z0为常数,所以求证关于z 的迭代收敛,可转换为求证z(θ2,θ3) 是关于θ3的增函数。

再次强调,因为ρ(θ3)的偏差是修正z(θ2)带来的,所以Δρ 的自变量是θ2；z(θ2) 的偏差是修正ρ(θ3)带来的,所以Δz 的自变量分别是θ3,这里二者自变量会互换。 通过分别对其相关变量求解偏导数,见公式(8),可以判断这两个函数的增减性。

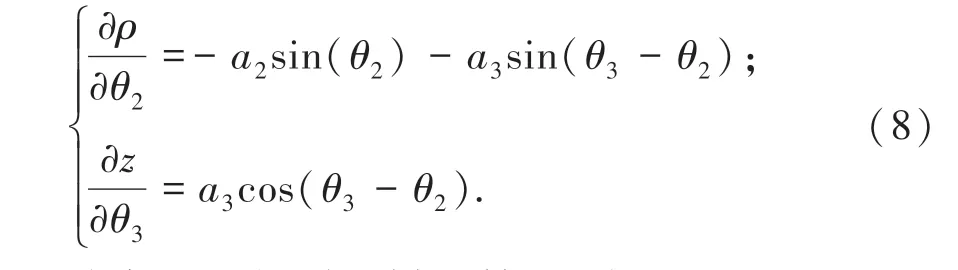
从中可以得到这样的结论：由于θ2∈(-π／6,π／2) ,θ3∈(0,5π／6),并且(θ3-θ2) ∈［0,π／2］使由此可以证明ρ(θ2,θ3)是关于θ2的减函数,z(θ2,θ3)是关于θ3的增函数,所以该迭代方法必然收敛。

2.3 对任意点的迭代

由于机械腿的运动范围是有限的,这意味着迭代存在一个可行域,超过可行域迭代必然无法收敛,下面着重讨论迭代的可行域

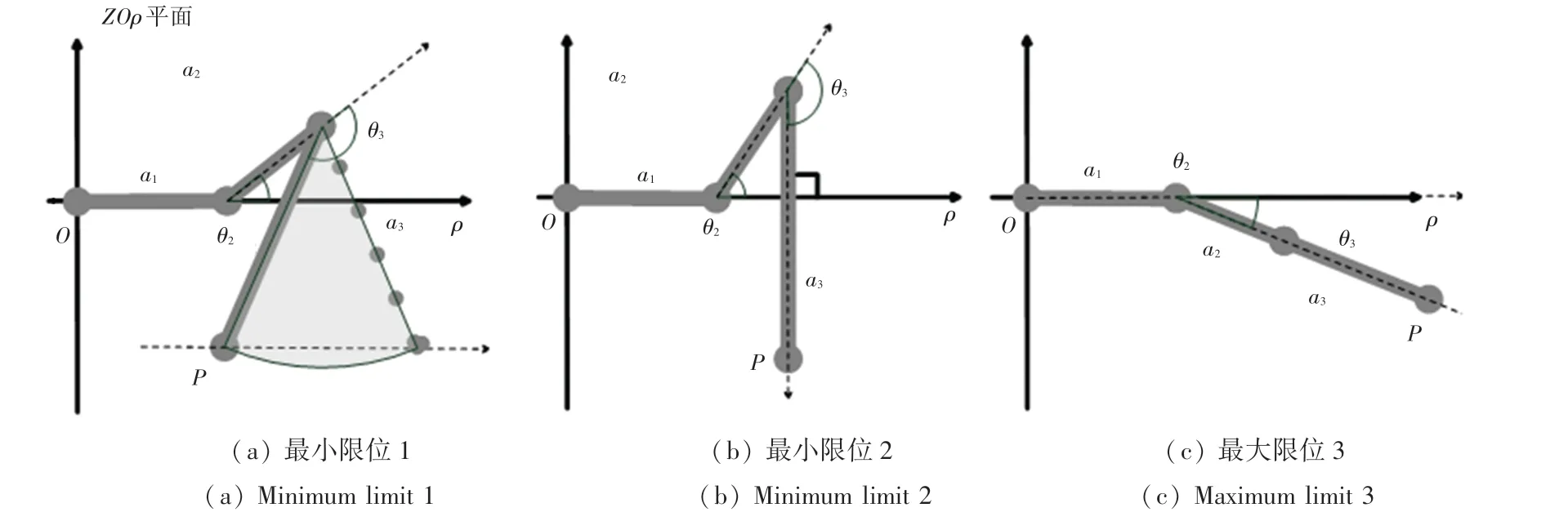
图3 可行域边界条件示意图Fig. 3 Boundary condition of feasible region

先要求取ρmin,由图3(a) 可以看出随着θ2继续减小,ρmin将进一步减小,但是由阴影部分可看出,这种方法会导致在恒定高度不变的情况下,P 点无法在z0平面内连续移动,这样会导致支撑面减小,影响机器人站立的稳定性,所以这里采用图3(b)的方式来求解ρmin。 如图3(b) 所示a3垂直于水平面,这时有(θ3-θ2)= π／2,ρmin的取值与z 和θ2有关,关系式为(9) 和(10)：

可以看出ρmin与ρmax都是关于z 的函数,由此得出3 条位于ZOρ 包络线,在两条包络线之间就是末端点P 可以运动的范围。 当(z ＋a3)／a2∈［- 1,1］时,ρmin曲线为ρmin= a1＋a2cos(θ2),如图4 中曲线(a) 所示。 当(z ＋a3)／a2＞1 时反正弦函数不再为实数,所以在z ＞47.11 时,θ2=arcsin((z ＋a3)／a2)不再适用,这时令θ2= π／2, ρmin曲线是以(a3, a2)为圆心a3半径的圆弧,如图4 中曲线(b)。 图4 中曲线(c) 为可行域最大边界的包络线。

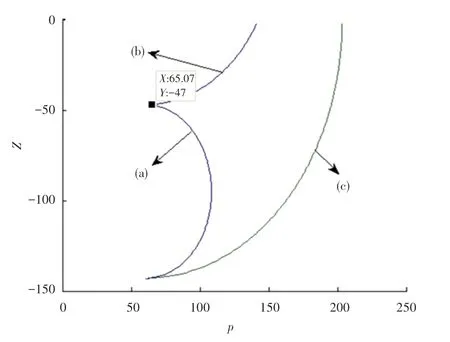
图4 可行域边界曲线示意图Fig. 4 Curves of feasible region

以空间内一点(120,0,-50)为例,进行24 次迭代后,各个参数变化如图5 所示。

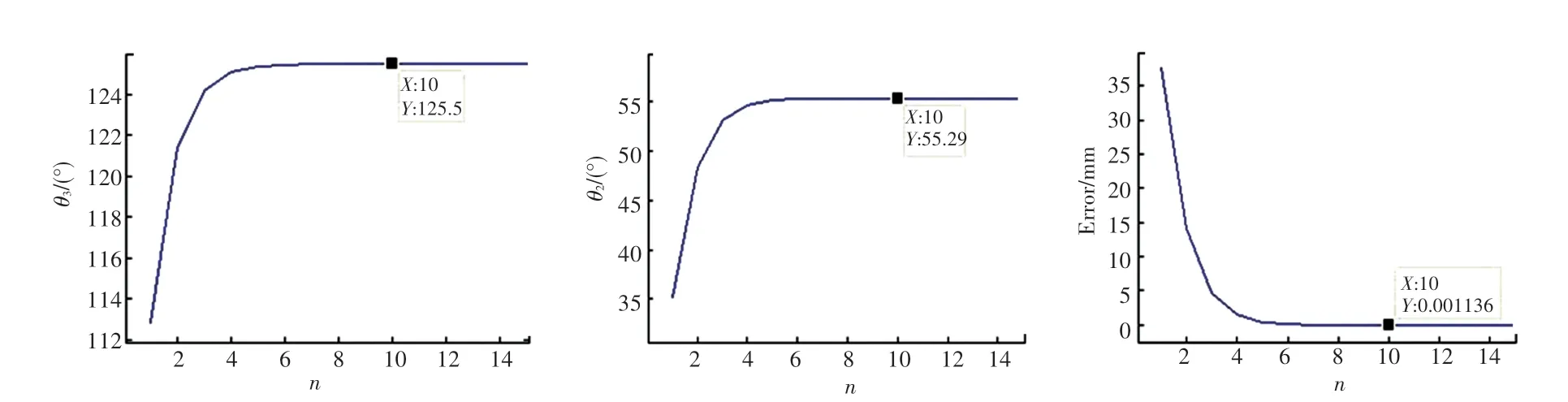
图5 单一点迭代各参数收敛情况Fig. 5 Iterative convergence issue of single point

如图5 所示,截取了前15 次迭代的结果,从中可以看到,在第十次的时候就已经达到了实际应用的标准。 经过10 次迭代,θ3收敛于125.5°,θ2收敛于55.29°,二者之差为70.21°＜90°,末端位置坐标与期望坐标误差收敛于0.001 136 mm。24 次迭代完成后x 收敛于120＋5.89×10-11mm,y 收敛于0.0 mm,z 收敛于-50-2.124 5×10-11mm,与期望坐标(120,0,-50)接近。

迭代过程如图6 所示,可以看出当对准z 轴时会使得ρ 产生偏差Δρ,并且Δρ 随着迭代的进行绝对值在逐渐减小,当对准ρ 轴时会使得z 产生偏差Δz,并且Δz 随着迭代的进行绝对值也在逐渐减小。 可以看出迭代收敛的范围,并不在目标点附近,所以该迭代方法对于初值的选取十分为宽松。

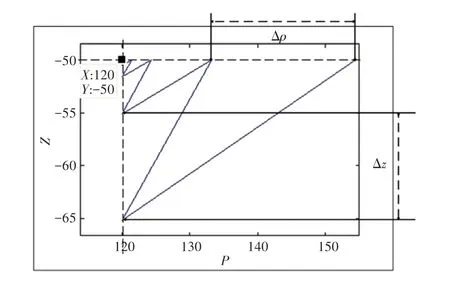
图6 单一点迭代过程Fig. 6 Iterative process of single point

为了研究点迭代的效果,在zoρ 平面内,每一个毫米取一个点,先保持z 不变逐行取点,然后z=z ＋1再继续取点,经过迭代,得到相对应的(θ3,θ2) 集合共40 000 组数据(其中7983 组数据误差小于0.000 1,为有效数据),回代到式(1) 中进行验算,绘制点结果如图7 所示,选取四组有代表性的数据如表2 所示结果。

表2 多点迭代结果比较Tab. 2 Comparisons among multiple points

这里存在一个必然的问题, ρmax是实际的最大可行域边界,而ρmin是根据实际情况定义出来的最小可行域边界,这意味着存在ρ ＜ρmin(最小值可以到0 附近,但是无实际用途),但是绝对不会出现ρ＞ρmax,当(ρ,z) 接近最大边界时,收敛效果会严重下降,即说明实际可行域内不可能存在这样一个点。 所以,如表2 所示第13039 号和26452 号点均在最大值边界附近,误差均大于一。 其中,图7 所示的第28210 号数据(在哪里？ ),由于同时靠近最大值和最小值边界,误差达到最大的37.12。 对于第13039 号点,尽管在最小边界附近,结果与期望的误差接近于零,在可行域内的第9860 和15085 号点,误差在允许范围内。 从28217 号数据到第40000 号均为无效数据,由于未被录入且初值为零,所以各项数据均为零。

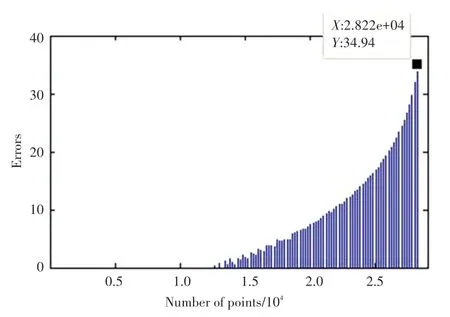
图7 多点迭代误差情况Fig. 7 Iterative error of multiple points

迭代点序数与误差关系如图7 所示,其中有明显误差的均为接近最大可行域范围的数值,由于序号越大,可行域越小,误差也逐渐增大。

以上是针对三关节机械臂进行求解的分析过程,对于多关节机械腿,该方法依然适用,其运动学正模型如式(12)所示。

同理可以利用本文所提出方法进行迭代求解,由于篇幅限制不再展开叙述。

3 结束语

本文巧妙利用了方程的非线性,做到了对点的精确快速迭代,对于更为复杂的几何曲线,可以在该曲线上取若干离散点,利用本文所介绍的迭代法逐一进行拟合得到每个关节输出角度的序列,机械腿依次执行,便可以拟合出该条曲线。 同时,如果该点在边界附近,误差会增大,大误差出现的频率会增加,所以选取这些点的时,可以利用误差剔除掉靠近边界的点,同时可行域范围可以适当缩减,z 取值范围可以控制在［0,100］。 并且该迭代法可以推广到更高自由度机械腿逆模型的求解上,有广泛的适用性。