考虑需求中断和购买者过度自信的应急物资动员链协调
史文强 孔昭君 汪明月
(1.北京理工大学管理与经济学院,北京 100081;2.中国科学院科技战略咨询研究院,北京 100049;3.俄勒冈州立大学工程学院土木与建筑工程系,美国科瓦利斯97330)
1 引言
近年来,各类自然灾害和人为灾害频发,对环境、人身财产安全和经济发展造成巨大破坏[1].应急物资是降低灾害损失的重要保障,是国家维持社会安全和稳定的重要基础资源.《国家突发事件应急体系建设“十三五”规划》提出了“应急物资综合保障能力快速提升”的目标,并将“完善应急物资保障体系”纳入主要任务当中.应急物资具有时效性强、需求不稳定和基数庞大等特性,在次生灾害下其需求容易产生爆发式增长[2],这对开展应急物资动员工作提出了较高的要求[3-4].为了减少灾害损失和挽救更多的生命,政府部门和动员机构需要向灾区提供应急物资,如医疗箱、水、食品、帐篷、预制房屋.应急物资动员链是以保障应急物资的超常规供给为目标,利用国民经济动员机制构建的应急物资供应链[5].
政府和相关社会团体是应急物资动员链中的购买者,动员物资的供应企业通常是有足够生产能力的大型公司或捐助者.然而大多数慈善组织和社会团体在灾难发生前都不具备足够的经济实力以采购或者储备大量的物资[2],故本文仅将政府机构视为采购方.这些主体的责任和利益可能会相互冲突.此外,灾害的破坏和应急资源的不足也给应急物资动员链的协调工作带来了重大挑战.合同和契约是协调商业环境中不同参与者的有效工具[6-9],只有少数学者将商业合同应用于救灾环境[10-13].突发式爆发增长的特点[12]使应急物资需求极易在频发的次生灾害下剧烈震荡.政府职能部门无法在第一时间准确获取需求量,仅能依据需求变化前的数据来安排应急动员任务,这可能直接导致需求发生中断.学者们从商业供应链入手,将需求中断界定为需求规模的突然增加或者减小,并认为需求中断会影响链上各参与主体[14-16].Ali等[17]运用Stackelberg博弈研究了市场需求中断对竞争零售商价格和服务水平的影响.Yan等[18]构建了需求中断情形下参与者风险规避的供应链定价、生产决策模型.Yang等[19]从信息角度入手,分析需求中断时信息模式对供应链绩效的影响.但上述文献皆未考虑需求中断如何影响灾害环境下的应急物资动员链(后文简称动员链).
过度自信是普遍存在于人们决策过程中的认知偏差.在这种偏差中,人们会过度相信自身的评估和预判能力,将不确定的结果当作更为精确[20].Li等[21]提出以过度自信水平为标准来衡量过度自信行为.当前学者主要从商业供应链视角关注过度自信问题.王新林等[22]考虑供需随机和企业过度自信,构建了批发价契约及期权契约下的供应链企业利润模型.Ren等[20]使用实验证明了人们对预测结果的过度自信会导致订单偏离最优均衡.Liu等[23]研究了需求更新下港口服务供应链的双重过度自信行为.当灾害爆发时,应急决策者无法准确地判断实际需求情况,可能会产生过度自信倾向,进而对灾区造成巨大影响.French和Niculae[24]认为在应急准备阶段存在过度自信.Hollnagel和Fujita[25]以福岛核电站事故为背景,发现专家对预测结果的过度自信阻碍了政府应急响应能力.包兴[26]在电力公司运营受损条件下,探索了惩罚援助机制如何减少过度精确和过高估计的影响.然而,上述研究并没有探索认知偏差如何影响灾害环境下应急物资的采购决策和系统协调.
应急物资动员的主要方式包括:强制征用、调用储备、应急采购、应急生产、社会捐赠和国际援助等[27].政府的行政(征用)手段给供应企业带来了巨大的压力和负荷[12],因此有必要在动员活动中引入市场机制.采购是应急物资保障过程中的重要一环[28].常规采购是购买者以事先约定的较低批发单价将应急物资采购到储备库当中的采购模式,具有成本低、配送迅速等特点[12].在需求中断情形下,仅靠常规采购无法满足灾区激增的需求,容易导致缺货风险[29].紧急采购(临时采购)是指购买者在常规采购的基础上,以新的采购单价追加额外的购买量,有助于减少需求不确定性的影响[30].在紧急采购模式下,供应企业需要提早准备生产,并预备一定的产能,故会设置高额的紧急采购单价[31].考虑到动员任务的紧急性和供应企业的产能,紧急采购量往往受到限制.较高的采购单价和有限的企业生产能力会导致紧急采购的低效,使政府在做采购决策时面临困境.因此在需求中断的环境下,将常规采购和紧急采购结合起来,协调应急物资动员链的采购过程具有重要的现实意义.
文献[11]与本研究较为相似,但并没有综合考虑需求模式、采购方式和决策者认知偏差,且其提出的期权契约不允许购买者在灾害中修改初始订单.本文引入的数量弹性契约允许购买者根据需求在一定比例(弹性契约参数)范围内调整初始订货量,有利于提升买方效用[13,32].该契约既给政府提供了紧急采购的机会,也限制了采购量的上限,在应急物资动员中具有一定的适用性.
如前所述,学者们对应急物资的研究主要是考虑参与者完全理性;另外,有关过度自信与需求中断的研究大部分是基于商业供应链背景,并没有考虑灾害情形下的需求满意效用.关于需求中断下、参与者为过度自信的应急物资动员链协调问题还鲜有学者涉及.鉴于此,本文在需求中断背景下,考虑政府机构过度自信时,运用数量弹性契约构建了具有紧急采购能力的应急物资动员链模型,分析其协调机制和最优订货决策,并与无需求中断情况和无过度自信的情况进行对比,探索常规采购单价、紧急采购单价、契约参数、过度自信水平等参数对政府最优购买决策的影响.丰富了不同情境下应急物资动员链协调的方法,为提升应急物资保障能力提供了科学的参考.
2 应急物资动员链模型
2.1 数学符号与模型描述
应急物资动员链是由单个供应企业、单个政府机构和单个受灾点构成.在灾害发生期间,政府很难实时确定实际需求信息,采购不当会使动员链产生库存过剩或缺货风险.政府机构和供应企业签订一组数量弹性契约,契约允许政府机构提出初始订单q(常规采购量),并在[(1-β)q,(1+α)q]范围内调整最终采购量.在初期,政府机构确定常规采购量,承诺至少订货(1-β)q.灾害发生中期,若出现缺货,政府实施紧急采购,但常规采购与紧急采购的总量不得超过(1+α)q.供应企业根据政府机构的采购策略,安排相应的常规生产和紧急生产计划.不失一般性,本文提出了以下假设:1)政府只与一家供应企业签订采购合同;2)在常规采购阶段,供应企业根据政府的初始订单制定生产计划;在紧急采购阶段,供应企业不直接提升到最大生产量,而是随政府最终订货量而动态调整;3)本文中政府不通过强制征用取得应急物资;4)政府机构与供应企业间的信息是对称的.应急物资动员链的结构如图1所示.

图1 应急物资动员链结构图Fig.1 The structure of emergency materials mobilization chain
假设X指灾区对应急物资的需求,是一个非负连续随机变量[2,11].在基准情况下(无需求中断)需求概率密度和分布函数分别为f(x),F(x),期望为µ.当需求中断时,需求的概率密度函数和累积分布函数变为h(x)和H(x),期望为µH.w(常规采购单价)和p(紧急采购单价)分别指常规采购和紧急采购模式下,政府向供应企业购买应急物资的单位价格.借鉴文献[11]和文献[13],将S定义为需求满足时政府的单位需求满意价值.契约上行系数α表示政府机构实际采购时可上调的订货量比例,下行系数β表示政府机构实际采货时可下调的订货量比例[32-33],即政府最低采购量不得少于(1-β)q,最多采购数量不得超过企业最大产量Q=(1+α)q.Moore and Healy[34]提出了3种不同类型的过度自信:过高估计、过高定位和过度精确.本文讨论第3种类型-过度精确,即政府机构过度相信自身的评估和预判能力,认为自己感知的不确定需求比实际情况更加准确.θ为过度自信水平,是衡量过度自信的标准,其阈值范围为0 ≤θ≤1[26].θ越大,过度自信政府机构眼中的需求方差越低于实际情况.
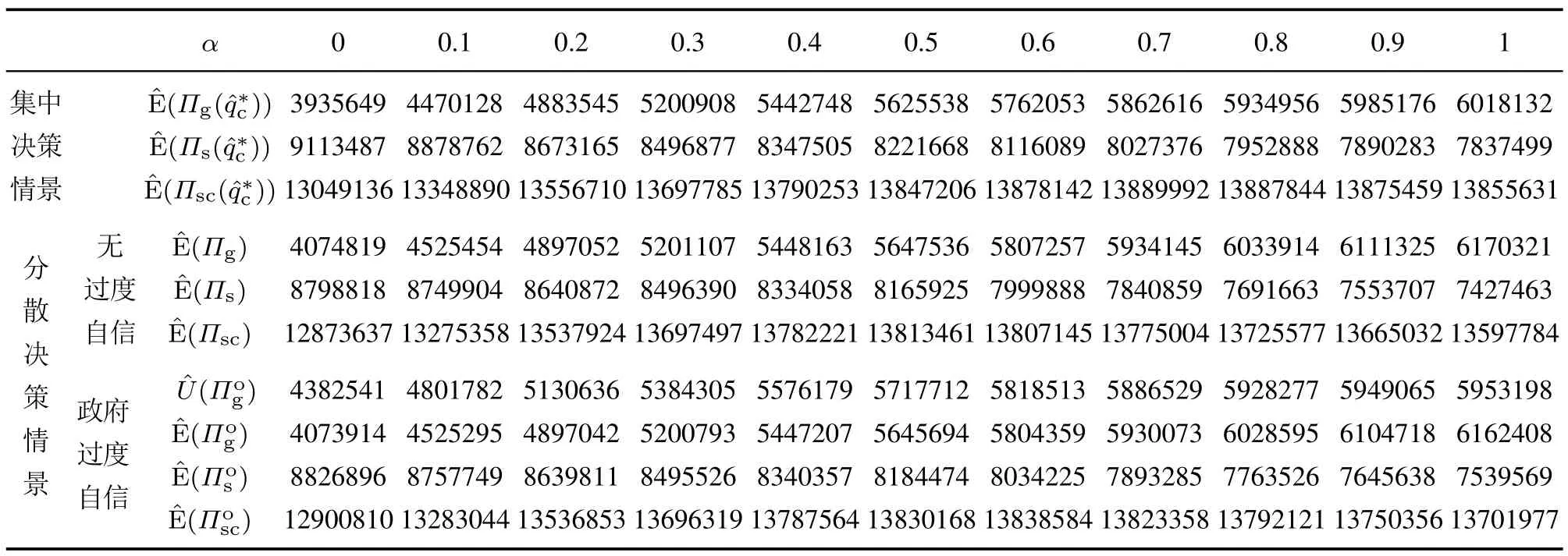
本文剩余的符号如表1所示.下标“g”,“s”和“sc”分别代表政府、供应企业和动员链整体,上标“*”代表最优解,上标“o”代表政府为过度自信的情况.参数满足如下关系式:v 表1 文中其余数学符号释义Table 1 The explanation of other mathematical symbols in the paper 本节在无需求中断的背景下,建立政府机构能进行紧急采购的数学模型.根据数量弹性契约的决策序列,政府机构的利润表达式如式(1)所示: 式(1)可以分为4个阶段:1)当需求非常低时,政府机构以常规采购单价履行最低订单量(1-β)q,并从需求满意价值中获益;未充分利用的救灾物资(1-β)q-x将按残值v回收;2)当(1-β)q≤x 因此,结合报童模型和随机期望理论,可得到政府机构的期望利润如式(2)所示: 供应企业利润函数可根据需求的差异分为4个阶段:1)当0 ≤x<(1-β)q,政府只购买常规订数量(1-β)q,而供应企业以常规生产成本制造初始订单量q.供应企业可以从常规采购量中获得收益,并从多余的产品量βq中获得残值;2)当(1-β)q≤x 动员供应企业的期望利润方程如式(4)所示: 根据式(2)和式(4),无需求中断时集中决策下应急物资动员链的期望利润方程可表述如下: 引理1整体应急物资动员链的期望利润是q的凹函数,最优订货量可由式(6)解得: 证明见附录. 次生灾害或者衍生危机对灾区造成冲击,进一步导致需求中断.需求中断会使政府无法准确预测激增的需求,产生供不应求的现象[17](如:新冠肺炎中的口罩、酒精和防护服等).由于灾害背景下需求激增产生的破坏和影响更为剧烈,故本文仅考虑需求增加的情况.假设需求激增后的分布函数和密度函数分别变为H(x)和h(x)(对∀x≥0,有),均值为µH,此时政府原本制定的订货决策将失去作用.为了应对需求中断,供应企业将增加最大生产量,每增加一单位产能将付出成本λ. 2.3.1 需求中断下无过度自信的模型 从集中系统来看,给定原始最大生产量为的前提下,需求中断时应急物资动员链期望利润为 其中:第1项表示系统获得的需求满足效用,第2项表示期末剩余物资的残值,第3项和第4项分别表示政府和供应企业的持有成本,第5项和第6项分别指供应企业的常规和紧急生产成本,第7项为物资缺货成本,λ()表示供应企业增加产能付出的总成本[35]. 引理2当需求中断时,集中决策下应急物资动员链的最优订货量可由式(8)解得 引理3当需求中断且政府机构无认知偏差时,若最优订货量满足式(11),分散决策中的政府机构的期望利润可以达到最大值. 2.3.2 需求中断下政府过度自信的模型 动员决策者并非完全理性的,他们可能有心理偏差和行为偏好.当次生灾害导致需求中断时,政府职能部门无法准确获知具体的需求变动情况,可能会高估自身需求预测能力,认为需求方差()比实际方差(σH)小.这种偏差导致买方将需求分布视作H(D),而不是H(x)[21].过度自信的政府机构感知到的需求可以由如下式表示: 其中:D是过度自信者感知到的需求,X是灾区实际需求,θ为政府机构的过度自信水平.随着θ的增长,政府感知到需求方差将更低于实际情况.如果θ=1,政府感知到的需求与实际需求的均值µH相等;θ=0指政府机构没有认知偏差.由式(12)可得到 尽管过度自信的政府决策者知道他们对需求认知与无偏见的决策者不同,但他们并不认为自身判断有误,仍然根据自己的估计做出决定[21].基于上述假设,可得出需求中断下过度自信政府机构的利润函数. 引理4当需求中断且政府机构为过度自信时,分散决策下的最优订货量可通过解式(15)求得: 证明见附录. 引理4表明,在需求中断条件下,当过度自信政府机构的订货量增大时,其期望效用先增大后减小.过度自信政府的最优采购策略受契约参数、缺货成本、过度自信水平等变量的影响. 动员物资供应企业是一个理性的主体,对需求预测没有认知偏差.在这种情况下,供应企业的期望利润方程与无过度自信情况下的相同. 政府和供应企业在分散决策时,是以自身利润最大化为目标,这可能会损害动员链整体的利润.集中决策模式下,政府和企业将作为一个整体共同决策,双方更关心整体利益,故集中决策下的订货量是整体系统最优的[11].因此,应急物资动员链协调的本质就是设计机制,使分散决策下政府最优订货量能达到集中决策下的状态 命题1在需求中断时,无论政府是否为过度自信,若合同参数(α,β)、常规采购单价(w)和紧急采购单价(p)按照一定方式进行调整,数量弹性契约下的应急物资动员链可以协调. 1) 在无过度自信的模型下,如果将α,β,w,p调整为满足式(17),则动员链可以协调. 2) 当政府机构过度自信时,若调整上述参数以满足式(18),需求中断下的应急物资动员链可以协调. 本节立足于需求中断情景,分析最优订货量随紧急采购单价p、常规采购单价w、上行系数α、下行系数β和缺货成本M变化的规律.由于p和w是政企之间交易的价格,并不影响系统整体决策,故本文在分析p和w时,仅探讨其对分散决策下订货量的影响. 命题2当需求中断时,理性或过度自信的政府机构的最优订货量随紧急采购单价p递增.理性政府机构的期望利润和过度自信政府机构的期望效用与p负相关. 本节命题过程详见附录. 命题2表明,在需求中断情形下,若p较高,政府机构在紧急采购时会承担更重的经济负担.此时,无论政府机构是否为过度自信,都更倾向于在初期阶段通过常规采购方式预定动员物资.因此,当分散决策的订货量低于集中决策的订货量时,提升紧急采购单价能促使政府增加常规采购量,进而与集中决策下的情况保持一致,反之亦然. 命题3在无过度自信或政府过度自信的模型中,需求中断下的政府最优订货量随着常规采购单价w增加而减少,政府机构的期望利润或期望效用也与w呈负相关. 命题3表明,在需求中断情形下,无论是否存在过度自信,若供应企业设置更高的常规采购价格,将减少政府机构的初始订单数量.随着常规采购量减少,在大规模灾害发生时,政府不得不通过紧急采购的方式订购更多物资.由于紧急采购单价远高于常规采购单价,所以政府机构的效用会受到间接损害.若分散决策下的最优订货量高于集中决策下的情况,供应企业需要提升常规采购单价,以保证分散决策下的订货量趋近于集中系统最优决策. 命题4在需求中断发生时,无论是集中决策还是分散决策,动员链系统的最优订货量和政府机构的最优订货量与数量弹性契约的上行系数α负相关,与下行系数β正相关. 命题4表明,集中决策下的最优订货量随α或β变化的趋势与分散决策情况相同.供应企业承诺的最大生产量越大,政府机构通过常规渠道购买的物资越少.同时,契约约定的最小订货量相对较小(即β较高),政府将提出较大的初始订单量. 命题5当需求中断时,集中决策下的最优订货量和分散决策下最优订货量都受到短缺成本M的正向影响. 命题5表示,动员物资缺货成本较高,就越能激励理性和过度自信的政府机构在初期阶段订购更多物资.在这种情况下,政府机构更担心库存不足,需要从常规采购渠道购买大量的物品,以减少紧急采购的额外经济成本. 本节以汶川8.0级大地震为背景,运用数值算例分析了需求中断下应急物资动员链协调机理,并探索了最优决策对不同参数的敏感性. 绵竹市是地震中受灾较为严重的城市之一,死亡人数达到11098人,受伤人数为36468人,急需帐篷以安置灾民.在灾害爆发初期,政府机构只能根据历史经验和地震烈度来估计需求分布.假设第1阶段政府判断帐篷需求服从[6000,10000]上的均匀分布,均值为µ=8000 顶,并据此向物资供应企业采购救灾帐篷.考虑采购的是3 m×4 m的民用救灾帐篷,每顶帐篷可容纳4-6人.依托《汶川特大地震抗震救灾志》、阿里巴巴平台中的数据,结合专家估计和访谈法,参数设置为:cs=400 元,ce=600 元,v=100 元,hg=hs=40 元,S=1600 元.若次生灾害和衍生事件进一步对灾区造成冲击,导致需求中断,需求规模增长为在区间[6000,22000]上的均匀分布,均值为µH=14000 顶,基本符合当地救灾中心发放的帐篷数(14300 顶),供应企业增加产能的单位成本为λ=300 元. 设置如下参数:w=1250,M=500,θ=0.2,α=0.3和β=0.2,定价的设置符合该类帐篷在阿里巴巴的销售价格区间.视p为变量,探索在需求中断下,如何调整紧急采购单价p以协调应急物资动员链,并分析最优订货决策和不同参与主体的期望利润关于p的敏感性. 图2-3描述了在需求中断条件下,无论是否存在过度自信,政府机构的最优订货量随紧急采购单价的增加而增加,而整个系统的最优订货量(集中决策)保持不变.分散决策下应急物资动员链的期望利润随p的增加呈现先增后减的趋势,存在固定协调点(=13679 顶或=13679 顶)使动员链利润最大化,这一现象与命题1-2一致.在过度自信条件下的动员链协调时,紧急采购单价将调整为p=1428.81 元,远高于非过度自信的情况.过度自信政府通常会比理性政府机构下更少量的常规订单,为了达到协调,供应企业应设置更高的紧急采购单价,以激励政府机构增加初始订单.在需求中断前,政府常规采购计划为=7566 顶,供应企业最大产能为=9836顶,应急物资动员链系统的期望利润为10153954 元.在需求中断后,若仍采用基准情形的定价机制,动员链期望利润仅为13694494 元,低于调整紧急采购价格后的系统利润13697785 元,无法实现动员链的协调. 图2 需求中断且无过度自信时p对和(Πsc)的影响Fig.2 The impact ofp on and (Πsc) in the situation of demand disruption and without overconfidence 表2表明,需求中断时,政府机构的期望利润和过度自信政府机构的期望效用皆与p负相关,供应企业期望利润均与p呈正相关.p的增加会促使政府提出更高的初始订货量,p和q共同增加将有利于供应企业的绩效.考虑到储备成本,政府机构不能在常规采购中购买量太大,增加p也会挤压紧急采购的空间,这使得政府机构在选择紧急采购和常规采购时会面临更多困难,进而影响其效用. 图3 需求中断且过度自信条件下p对和()的影响Fig.3 The impact ofp on and () in the situation of demand disruption and with overconfidence 在需求中断时,过度自信政府机构的期望利润低于其自身期望效用和无过度自信下的期望利润.过度自信偏差使政府机构乐观地估计受灾地区的需求,错误地认为其利润大于理性的政府机构.这种现象进一步导致过度自信政府机构的常规采购量和利润减少. 表2 需求中断时,p对动员链各参与方期望利润的影响Table 2 The impact ofp on the participants’expected profits in the mobilization chain under demand disruption 当其余参数不变时,设p=1350 元,将α和β视为变量.首先,讨论了通过调整契约参数来协调应急物资动员链.然后,研究α和β如何影响政府机构的最优采购决策和不同成员的期望利润. 图4中,在需求中断下,当代表整个系统最优订货量的曲面(即集中决策曲面)与其他两个曲面相交时,就存在一组α和β能够协调应急物资动员链.集中决策下的曲面与过度自信情况下的曲面相交较多,与理性政府订货量的曲面交叉较少.这表明过度自信的情形有更多契约参数组合能够协调动员链.无论是集中决策还是分散决策,最优订货量都随上行系数α增加而递减,随下行系数β增加而递增.究其原因,增加α为政府机构提供了更大的补货空间,降低了其对缺货的担忧.此时,政府机构更倾向于选择较少的初始订货量.相反,增加β能允许政府机构在更大范围内减少最低订货量,减少库存过剩的风险,政府更倾向于提前购买更多的物资. 当分别固定β=0.2和α=0.3时,过度自信情境下的上、下行系数的协调值(α=0.341,β=0.216)皆高于无过度自信的情况(α=0.315,β=0.206).由表3可知,当需求发生中断时,无论是集中决策还是分散决策,增加契约上行系数α都会降低缺货风险,故政府机构的期望利润随α递增.而供应企业在生产和持有额外应急物资时要承受更大的经济负担,其期望利润随α递减.表4说明政府机构和供应企业的期望利润与下行系数β不存在单调关系.由于β的增长将加剧供应企业库存过剩的风险,因此政府机构不会盲目地增加初始订货数量,以防供应企业拒绝合同.较小的β可令政府的最小订货量接近其初始订货量,降低供应企业对过量生产的担忧,所以当β=0时,供应企业将获得最大利润. 图4 需求中断时,α和β对最优订货量的影响Fig.4 The impact ofα andβ on the optimal order quantity under demand disruption 表3 当β=0.2时,α对动员链各参与方期望利润的影响Table 3 Whenβ=0.2,the impact ofα on the participants’expected profits in the mobilization chain 表4 当α=0.3时,β对动员链各参与方期望利润的影响Table 4 Whenα=0.3,the impact ofβ on the participants’expected profits in the mobilization chain 设α=0.3,β=0.2,并将w视为变量,保持其余参数不变.首先,讨论了不同常规采购单价下应急物资动员链的协调机制.其次,分析了动员链中参与方期望利润对w的敏感性. 需求中断前政府的最优常规采购单价为w=1341.31 元,若需求中断后仍采用基准情形下的定价机制,分散决策下动员链利润仅为13663946 元,远小于集中系统的利润13697785 元,无法实现动员链的协调.如图5-6所示,在需求中断时,政府机构的最优订货量与w负相关.无过度自信的动员链在w=1240.56 元实现协调,而过度自信情形下的动员链的期望利润在w=1222.16 元达到最大值.过度自信政府机构根据不准确的需求判断,倾向于提前购买少量应急物资.此时,降低常规采购单价能有效增加常规采购量,弥补需求中断和过度自信所导致的决策偏差. 图5 需求中断且无过度自信时w对和(Πsc)的影响Fig.5 The impact ofw on and (Πsc) in the situation of demand disruption and without overconfidence 由表5可知,理性政府机构的期望利润、过度自信政府的期望利润与效用皆与w负相关.随着w上涨,供应企业期望利润会增加.对于政府机构来说,增加w会导致单位物资的效用减少,对常规采购数量产生负面影响.在此前提下,政府机构倾向于通过紧急采购方式获取更多物资.政府机构的利润会随着常规采购数量的减少和常规采购单价的提高而受损,增加紧急采购数量和常规采购单价的双重作用促使供应企业利润增加. 图6 需求中断且过度自信条件下w对和()的影响Fig.6 The impact ofw onand ()in the situation of demand disruption and with overconfidence 设w=1250 元,并将M视为变量,保持其他参数不变.表6分析了需求中断下最优订货决策和参与者期望利润对M变化的敏感性. 在需求中断情景下,无论政府是否为过度自信,政府机构的最优订货量、各参与方和整个动员链的期望利润与缺货成本M正相关.其原因是增加M使政府机构承担更多的缺货损失,进一步促使政府机构从常规采购渠道购买更多物资.理性和过度自信政府机构的最优订货量之差随M增加而递增.无过度自信下应急物资动员链的期望利润与过度自信情况的期望利润之差也与M正相关.这说明增加缺货成本放大了过度自信的影响,使政府的最优决策量和动员链期望利润更大程度地偏离正常状态. 表5 需求中断时,w对动员链各参与方期望利润的影响Table 5 The impact ofw on the participants’expected profits in the mobilization chain under demand disruption 表6 需求中断时,最优订货量和期望利润对M变化的敏感性Table 6 The sensitivity of optimal order quantity and expected profits toM under demand disruption 设M=500,保持其他参数不变,分析政府最优订购决策和参与者期望利润对θ的敏感性. 由表7可知,随着过度自信水平的提高,需求中断情形下的最优订货量、各参与方和整个动员链的期望利润都会下降.更高的过度自信程度使政府将灾区的实际需求视为一个更稳定、波动更小的需求,政府感知到的期望效用反而增大.这种不确切的判断可能导致政府机构放松警惕,减少初始采购订单数量.在其他因素不变的情况下,初始订单数量的减少会对每个参与方和整个动员链的利润产生负面影响. 表7 需求中断时,最优订货量和期望利润关于θ的敏感性Table 7 The sensitivity of optimal order quantity and expected profits toθ under demand disruption 表7还说明增加过度自信水平会对不同情境下最优订单数量之差产生正向影响,应急物资动员链期望利润之差也随着θ递增. 考虑灾情动态变化,设需求分别为[6000,22000],[5000,21000],[7000,23000],[6500,21500]和[5500,22500]范围上的均匀分布,分析不同需求均值和方差下,动员链协调策略的调整与变化情况. 表8表明,无论政府机构是否为过度自信,随着灾区需求规模的增加(即µH增大),协调时的常规采购单价和初始订货量将随之增大;而协调时的紧急采购单价、契约下行系数和上行系数都将减小.面对激增的需求规模,政府机构在分散决策时会提高初始订货量,大于集中系统的最优决策.供应企业为了维护自身利润,会适当降低p或提升w.另外,降低契约弹性系数α,β以压缩政府的订货空间,也能保证供应企业利润不会过度受损. 当需求分布的方差增加,在弹性契约系数不变的情形下,政企双方会采取加大初始订货量和提高紧急采购价格(或降低常规采购价格)的方式以实现协调.为了应对需求不确定性的增加,提升契约上行系数并降低初始订货量(或提升契约下行系数并增加初始订货量)也是可行的协调策略.其中,提升上行系数α增大了政府的补货空间,降低了缺货的风险,在需求更加不稳定的前提下,政府会适当减少初始订货量以达到动员链系统利润的最大化. 表8 需求变化下的应急物资动员链协调值Table 8 Coordination value of emergency materials mobilization chain under demand changing 本文考虑需求中断情景,引入紧急采购环节,构建了数量弹性契约下政府机构为过度自信的应急物资动员链模型,探索如何调整定价机制和契约参数以实现协调.结合无过度自信的情况,研究了契约参数、常规采购单价、紧急采购单价、缺货成本和过度自信水平对最优订货决策的影响.最后依托救灾帐篷的需求背景,运用数值分析检验了协调机制,并对相关变量进行了灵敏度分析,得出的结论和管理学启示,为动员任务的决策者提供可靠依据. 1) 需求中断发生后,若仍然采用基准情况下的定价和契约,无法协调应急物资动员链.无论政府机构是否为过度自信,数量弹性契约下的应急物资动员链可以通过调整契约参数、紧急采购单价和常规采购单价来协调.这一结论较前人的研究有一定提升,学者们运用不同契约探讨了救灾供应链的协调问题[11,13],但没有将紧急采购和参与者认知偏差纳入考虑.部分学者设计了过度自信管理者应急决策的纠偏机制[26],但仅以单个决策者的应急成本为目标函数,未讨论多个主体间的协调问题.本文立足于的前人研究,考虑过度自信和紧急采购会影响需求中断下应急物资动员链的最优决策,阐明了数量弹性契约的协调条件. 2) 政府机构最优订货量和各参与成员的期望利润随过度自信水平的增加而减少.同时,政府的过度自信态度会加大不同认知偏差下动员链期望利润之差,这一观点与文献[26]类似.然而,文献[26]认为在某些情况下,过度精确行为会减少管理者的决策偏差,这与本文有较大不同.本文发现过度自信政府会依据自身感知到的需求进行决策,从而提出更少的初始订货量.随着过度自信水平增长,过度自信政府和理性政府之间的最优订货量偏差就更大.引入数量弹性契约和紧急采购既增加了政府采购的灵活性,也为实现系统最优提供了更多选择.从企业管理者角度来看,为了减少过度自信政府的决策偏差,供应企业可以上调紧急采购单价、降低常规采购单价,或采用调整弹性契约参数的方式,使政府决策下的最优订货量接近系统最优决策.从政府监管角度来看,应通过教育和培训来强化自我归因和认知再评价的理念,并加强收集个人信息和反馈,使动员工作者重新思考并充分认识自己的错误估计倾向[36]. 3) 在需求中断时,政府最优订货量和各参与方的利润皆随缺货成本的增加而递增.上层政府决策者可以通过加大缺货惩罚力度的方式,提升采购和生产的积极性,减少应急物资供应不足现象.但是,增加缺货成本会使过度自信政府的最优订货量更大程度地偏离正常状态.因此,在上级政府加强缺货惩罚的同时,供应企业也需要增大采购价格和契约参数的调整幅度,以保证动员链协调. 4) 随着需求均值增长,政企双方在增加初始订货量的同时,需分别采取降低紧急采购单价、契约参数或提升常规采购单价的策略.当需求方差增加时,为了协调动员链,在政府增大初始订货量的同时,供应企业可分别降低常规采购单价、上调紧急采购单价或契约下行系数. 本文是探索应急物资动员链紧急采购和认知偏差的重要一步,但在实际应用中仍然存在一些不足.未来的研究应该将多个竞争供应企业和动员努力程度纳入模型,并考虑所有参与者都存在过度自信偏差.另外,不同参与者之间信息不对称的动员链协调机制也有待进一步研究. 附录 引理1证明 证根据一阶最优选择条件,计算式(5)关于订货量的q一阶及二阶导数,可得 因为v 证毕. 引理2-3证明 与引理1类似,通过一阶最优条件,直接求导后可得,略. 引理4证明 计算式(14)关于q的一阶导数,可得到如下方程: 命题1证明 对于需求中断且政府机构为过度自信的应急物资动员链,判断协调的依据为[13].控制其他参数不变,判断如何调整p值,使分散决策下的订货量等于集中决策下的最优解时,过度自信政府机构的期望效用关于q的一阶导数等于零.将集中决策下的最优订货量代入分散决策下政府最优订货量的表达式(15)中,并令其等于零,合并同类项后得到式(18).求解上述方程,可得到调整后的紧急采购单价.若存在使等式(18)成立,分散决策下的最优订货量就与集中决策的状态相一致,即实现动员链协调.同理,调整后的契约参数及常规采购单价也可从式(18)求得.无过度自信的模型与过度自信情况类似,证明过程略. 证毕. 命题2证明 1) 在无过度自信情况下,取式(A6)关于q和的p一阶导数,可分别得到式(A8)和式(A9): 运用代数方法可推知式(A8)为负数,而式(A9)为正数,进一步求得因此随p递增. 2) 按照同样的逻辑,取式(A7)关于q和p一阶导数. 证毕. 命题3证明 命题3的证明与命题2步骤类似,故不再深入讨论. 命题4证明 分别求解式(A5)-(A7)关于α的一阶导数. 命题5证明 命题5的证明与命题4步骤类似,故不再深入讨论.
2.2 基准模型
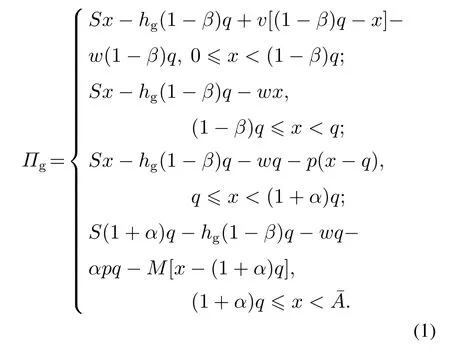




2.3 需求中断的应急物资动员链模型


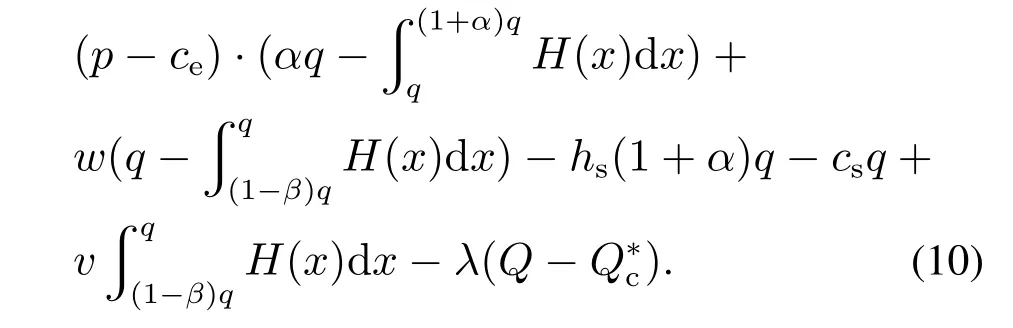

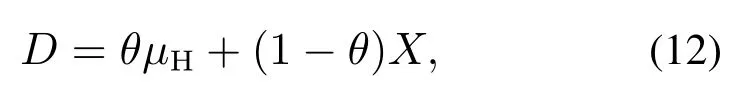






3 协调机制及参数影响
3.1 不同情况下的协调机制

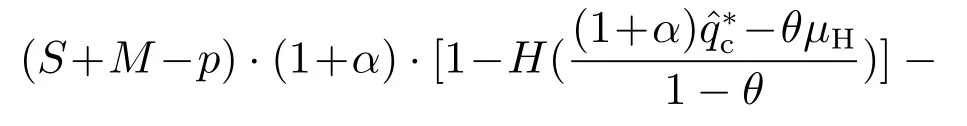

3.2 最优订货决策随相关参数变化的情况
4 数值算例分析
4.1 紧急采购单价(p)对最优决策和利润的影响



4.2 弹性契约的上行和下行系数(α,β)对最优决策和利润的影响


4.3 常规采购单价(w)对最优决策和利润的影响


4.4 缺货成本(M)对最优决策和利润的影响


4.5 过度自信水平(θ)对最优决策和利润的影响

4.6 灾区需求变化对协调值的影响

5 结束语








