矿用腕部偏置伸缩型Pieper机器人新算法数值解研究
姚海峰,刘伟,郑晓雯,张兰胜2,,刘福新2,,吴淼
1.中国矿业大学(北京) 机电与信息工程学院,北京 100083;2.河北省煤矿机械工程技术研究中心,河北石家庄 051431;3.石家庄煤矿机械有限责任公司,河北石家庄 051431
机器人工作时需要对各关节参数进行实时控制,对各关节的运动进行精度补偿,因此机器人各关节的逆运动学求解十分重要[1-3]。工业机器人多为6个自由度机器人,前端肩部3个自由度用于确定位置,后端腕部3个自由度用于确定姿态,可以在运动范围内任意定位与定向[4]。
已证明只有2种构型机器人的运动学逆解是封闭的,一类是存在3个连续相交轴的Pieper型机器人,一类是存在3个连续平行轴的Duffy型机器人[5]。机器人逆运动学求解一般有3种方法:代数法、几何法和DH法[6-8]。代数法和几何法适用于少自由度机器人,其关节之间要满足一定条件[9];对于6个自由度机器人当前应用较广的是DH方法。
为得到简易的封闭逆解,多数工业机器人构型满足Pieper条件,这类机器人即球型腕部机器人。在国内外的相关文献[2,10-13]中讨论的都是这种球形腕部机器人,这种构型存在不能承受较大负载的缺陷。为解决这一问题,采用腕部偏置机器人的结构形式[14]。当前对腕部偏置型机器人运动学求解的研究多借助于复杂的数值计算求解,文献[14-19]中认为不存在解析解,须通过优化、迭代或神经网络等方法求取数值解。这些方法往往计算时间长且精度较差,不利于工业性应用。
本文对复杂的腕部偏置型机器人进行研究,该机器人用于掘进机截割头焊接和井下凿岩,为了增大工作范围和灵活性,在执行端采用滑动构件使得其运动学求解更为复杂。笔者结合迭代搜索求解的思路采用一种有别于传统DH方法的全局坐标系递次归位的算法进行求解,该方法计算耗时短、精度高,可促进腕部偏置型机器人工业应用的实现。
1 建立全局坐标系
各种文献中常见的PUMA560机器人和斯坦福机器人都属于典型的球型腕部机器人,其构型如图1所示。
腕部偏置伸缩型Pieper机器人构型和结构如图2所示,图2(a)为构型,图2(b)中用不同颜色箭头表示各矢量轴。其中红色构件为动件1,绕矢量轴1旋转,即第1自由度,其参数值为θ1;橙色构件为动件2,绕矢量轴2旋转,即第2自由度,其参数值为θ2;以此类推。蓝色构件为动件6,沿矢量轴6滑动,即第6自由度,其参数值为L6。
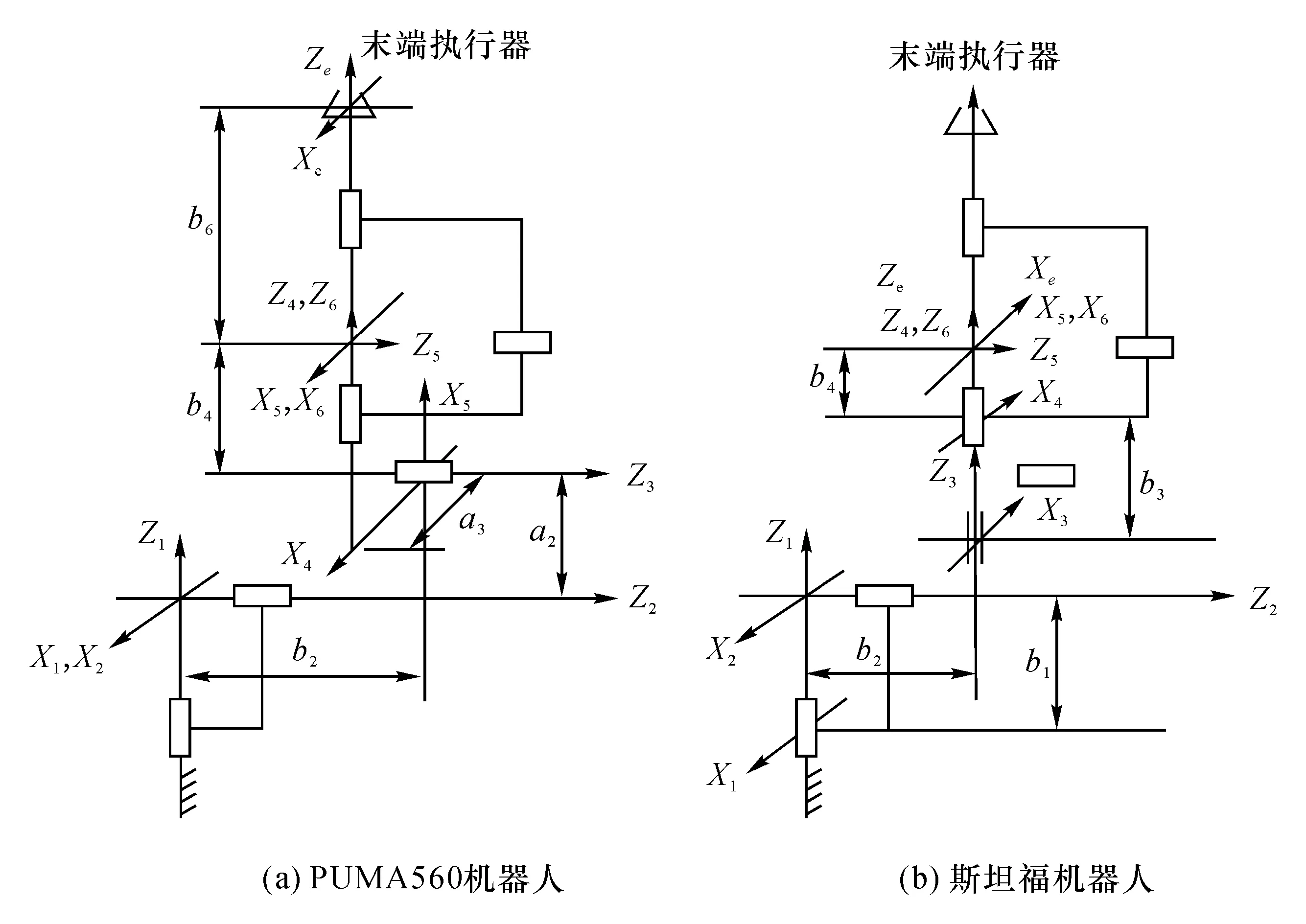
图1 PUMA560机器人和斯坦福机器人构型Fig.1 Architecture of PUMA560 and Stanford robot
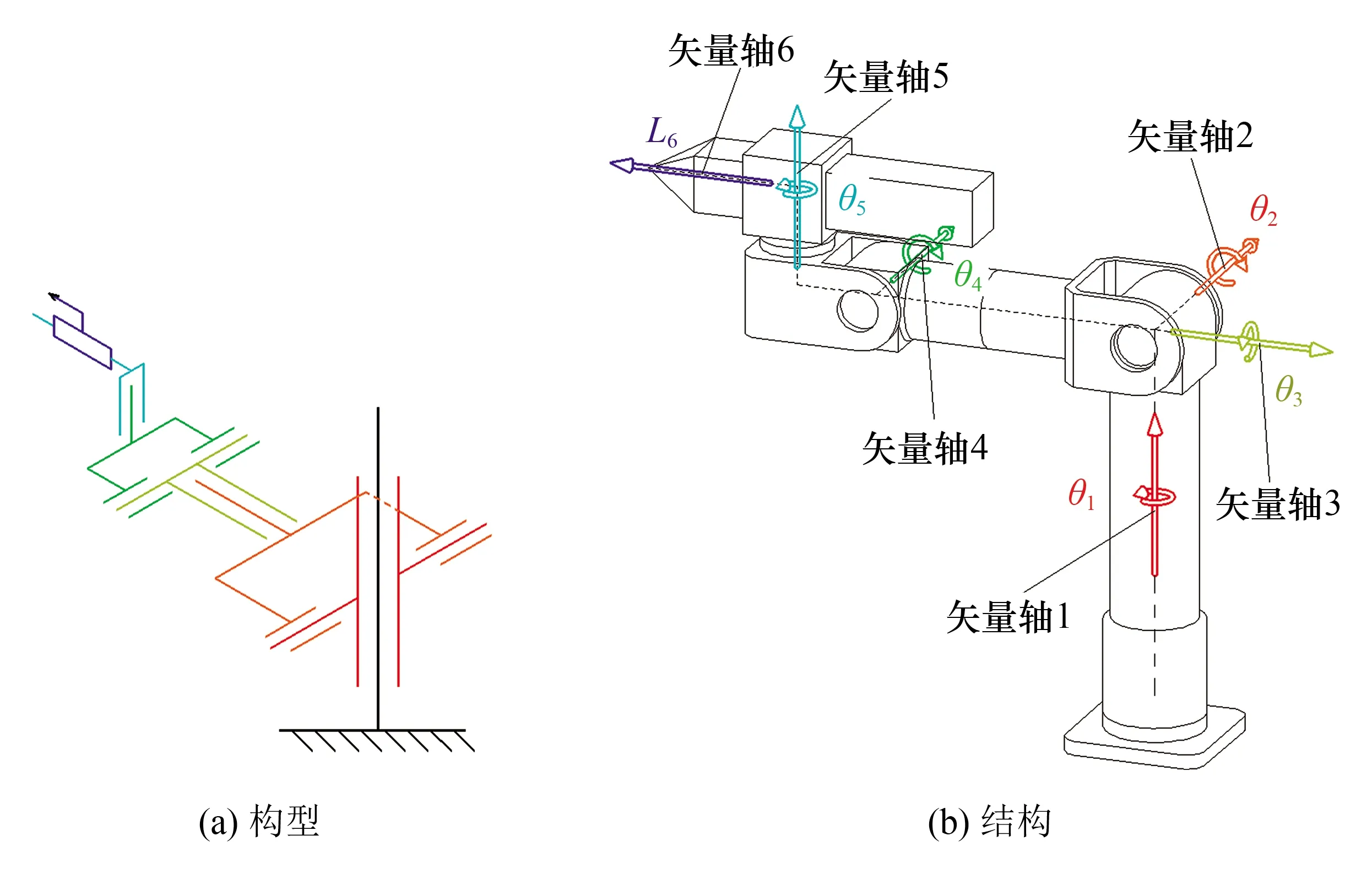
图2 腕部偏置伸缩Pieper机器人构型和结构Fig.2 Architecture and structure of wrist offset Pieper robot with prismatic link
腕部偏置伸缩型Pieper机器人矢量轴1、矢量轴2和矢量轴3相交于一点,符合Pieper条件;矢量轴4、矢量轴5和矢量轴6处于偏置交错状态,且第6自由度为伸缩动作,因此其运动学逆向求解不同于传统结构。
1.1 全局坐标系
机器人初始位置全局坐标系如图3所示,其中a1为矢量轴2与矢量轴4之间距离,a2为矢量轴4与矢量轴5之间距离,d1为矢量轴3与矢量轴6之间距离,这3个值为固定结构尺寸。a3为动件6相对于动件5未伸缩时动件6前端尖点与矢量轴5之间距离,该尺寸值根据机器人工作状况可以调整,但调整好后在机器人作业过程中该值固定不变。
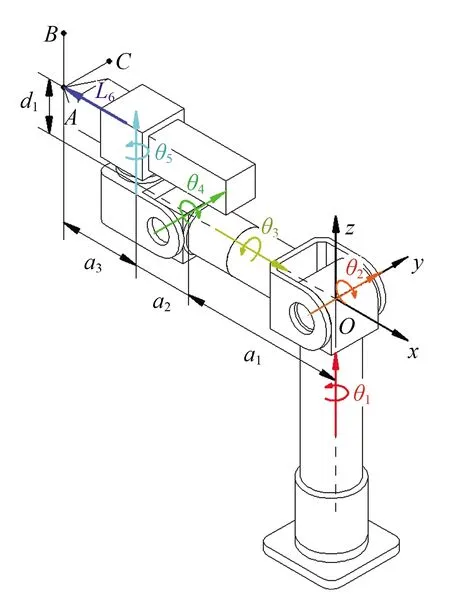
图3 全局坐标系和关键结构参数Fig.3 Global coordinate system and the key structure parameters
各矢量轴由各自轴上空间两点坐标值确定,因此在起始位置有:矢量轴1由原点指向点(0,0,1),矢量轴2由原点指向点(0,1,0),矢量轴3由原点指向点(1,0,0),矢量轴4由点(-a1,0,0)指向点(-a1,1,0),矢量轴5由点(-a1-a2,0,0)指向点(-a1-a2,0,1),矢量轴6由点(-a1-a2-a3,0,d1)指向点(-a1-a2,0,d1)。
1.2 基础公式
在全局坐标系中进行点的空间变换求解有 2种:一是计算空间一点绕空间矢量轴旋转给定角度后该点坐标;二是计算空间一点沿空间矢量轴移动给定距离后该点坐标。
假定空间点为I(x,y,z),空间矢量轴由点J(x1,y1,z1)指向点K(x2,y2,z2),进行上述2种运算。令
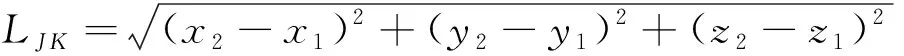
点I沿矢量rJK移动距离l变为I′(x′,y′,z′),有
(1)
点I绕矢量rJK转动θ变为I″(x″,y″,z″),有
(2)
式中,cθ为余弦cosθ;sθ为正弦sinθ。
2 全局坐标系求解
2.1 正向求解
在执行末端(动件6)选定3点A、B、C,以其空间坐标值表述执行端位姿。A点设定在尖端处,初始位置坐标值为(-a1-a2-a3,0,d1),B点坐标为(-a1-a2-a3,0,d1+t),C点坐标为(-a1-a2-a3,t,d1),其中t值任意给定,给定后其值固定。
正向求解是已知各关节角度值求解A、B、C三点最终坐标。计算时先求第6自由度完成后各点坐标值,然后计算第5自由度完成后各点坐标值,以此类推即可计算出第4至第1自由度完成后各点坐标值。现以点A为例,其计算公式如下:
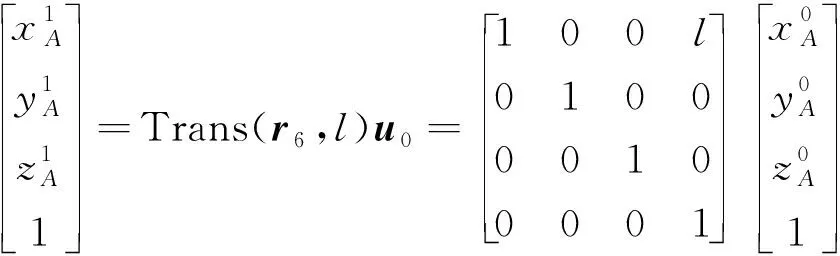
(3)
2.2 逆向求解
2.2.1 迭代求解L6值和θ5值
直接通过式(3)进行逆向求解是无法实现的,必须结合腕部偏置伸缩Pieper机器人空间构型才能进行求解。
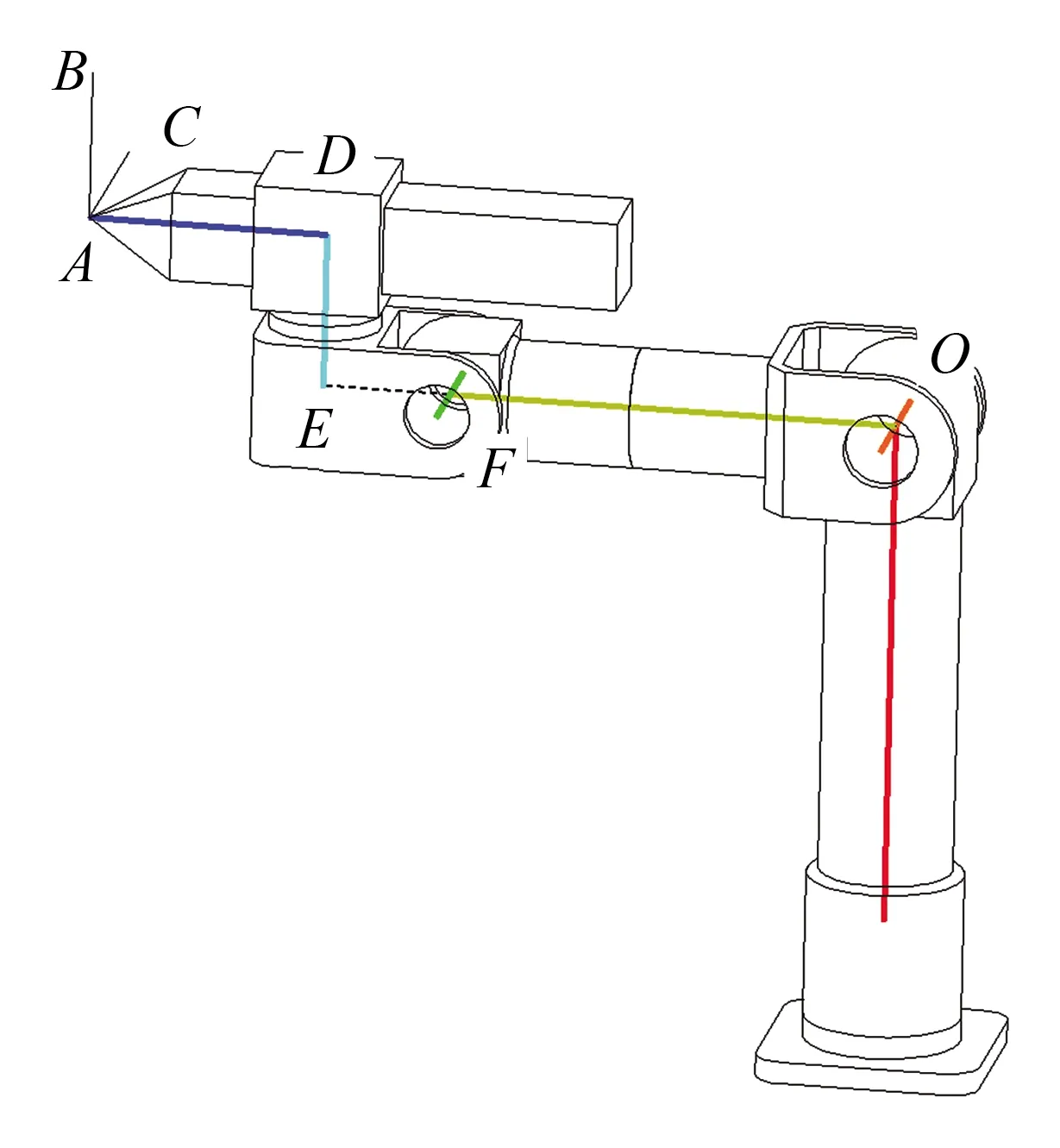
图4 逆向求解关键点Fig.4 Key points of inverse kinematics
如图4所示,在执行端(动件6)上再选定D、E、F三点。D点为矢量轴5与矢量轴6的交点,在初始位置时AD之间距离为a3;E点为矢量轴3与矢量轴5的交点,DE之间距离恒定为d1;F点为矢量轴3与矢量轴4的交点,EF之间距离恒定为a2;O点为坐标原点,OF之间距离恒定为a1。
由图4可知,F点为求解关键点,当该点空间坐标确定时,θ1、θ2、θ3即可求出,因此逆向求解思路第一步是求解该点空间坐标值。
给定6个自由度参数值的机器人空间状态如图5所示。由图5可知,由A、D、E三点确定的平面Ⅰ和由原点O和矢量轴5所确定的平面Ⅱ之间夹角(区分正负)为第5自由度参数值θ5,因此求解该两平面之间夹角转化为求解线AD与平面Ⅱ法线之间夹角。
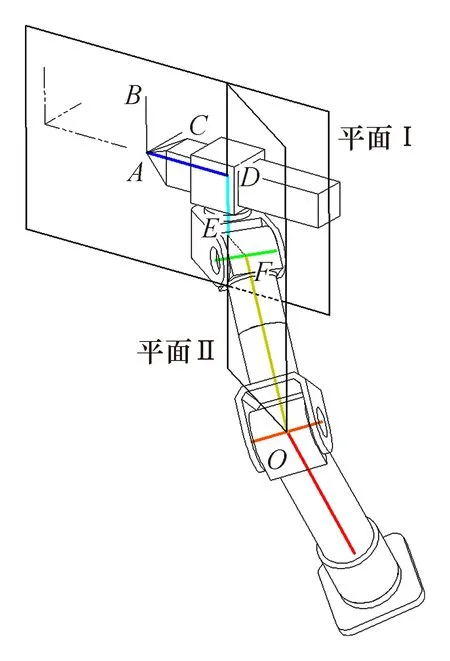
图5 各动作完成后空间状态Fig.5 Ultimate spatial state
如果将动件6沿矢量rAD后移合适的距离l使得DE与矢量轴5重合,此时将F点绕DE轴线旋转-θ5使F点与矢量轴3、矢量轴4交点重合。动件6逐渐后移时采用前述方法计算所得的点F到O点之间距离的绝对值|OF|是先缩小后增大的,后移的目的是使F点与矢量轴3、矢量轴4交点重合,此时F点与O点之间距离为定值a1,因此可采用迭代方法计算出L6值和θ5值。
迭代求解L6值和θ5值流程如下:
A、D、E、F四点均位于执行端上,在逆向求解时执行端位姿是确定的,因此四点在全局坐标系内坐标值也是确定的,分别为A0(A0x,A0y,A0z),D0(D0x,D0y,D0z),E0(E0x,E0y,E0z),F0(F0x,F0y,F0z)。
各点沿矢量rA0D0移动l的变换矩阵为
(4)
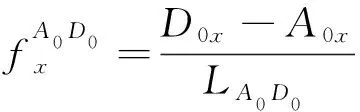
动件后移完成各点坐标如下:
由于直线DE为两平面交线,因此将求平面Ⅰ和平面Ⅱ之间夹角转化为求空间直线AD与平面Ⅱ法线的夹角,直线AD平行向量与平面Ⅱ法线向量分别为
(5)
平面Ⅰ与平面Ⅱ法线的夹角为
(6)
将点F绕矢量E1D1转动-θⅠ-Ⅱ得
(7)
此时F点到O点的距离:
(8)
将上述计算流程整合为函数f_iteration,返回值为
f_iteration(l)=|OF2|-a1
通过迭代方法重复以上过程,lmin初始值为 -500,lmax初始值为0,设定判定条件为10-8。迭代流程如下:
fmin=f_iteration(lmin)
fmid=f_iteration(lmid)
fmax=f_iteration(lmax)
该循环完成后判断|fmid|<10-8是否成立,如成立则循环结束,如不成立则重新对lmin和lmax赋值并进行下一步循环。赋值判别条件为:如果本循环所得fminfmid<0,则将当前的lmid值赋予下一步的lmax初始值;如果fmidfmax<0,则将当前的lmid值赋予下一步的lmin初始值;当|fmid|<10-8时计算完成,得到L6=lmid,θ5=θlmid。
2.2.2 递次归位方法求解θ1、θ2、θ3和θ4
第6自由度L6和第5自由度θ5求解完成后,先后将第6和第5自由度归至0位,有
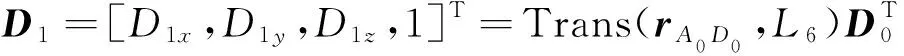
第6和第5自由度归至0位后机器人空间状态如图6(a)所示,由其俯视图可计算出θ1,有
(9)
将第1自由度归至0位,有
第6、第5和第1自由度归至0位后机器人空间状态如图6(b)所示,由其主视图可计算出θ2,有
(10)
将第2自由度归至0位,有
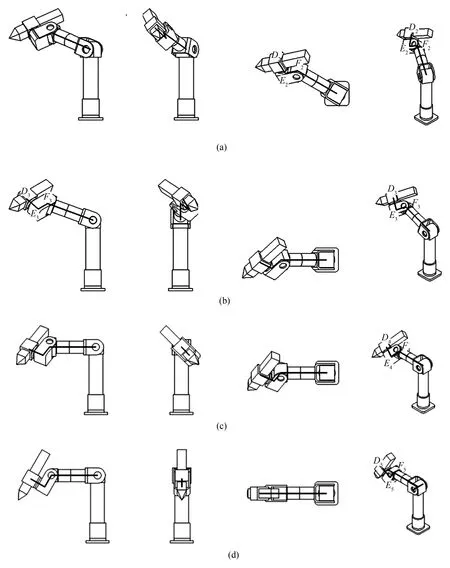
图6 归位过程中机器人空间状态Fig.6 Spatial states of the robot in returning process
第6、第5、第1和第2自由度归至0位后机器人空间状态如图6(c)所示,由其左视图可计算出θ3,有
θ3=arctan 2(D4z,D4y)
(11)
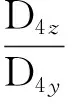
将第3自由度归至0位,有
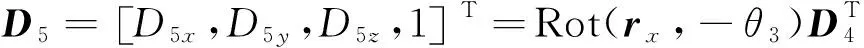
第6、第5、第1、第2和第3自由度归至0位机器人空间状态如图6(d)所示,由其主视图可计算出θ4,有
(12)
3 验证和应用
3.1 正向验证
各动作参数值设定为:θ1=5°、θ2=-10°、θ3=15°、θ4=-20°,由其左视图可计算出θ5=25°、L6=30,由式(3)得
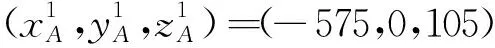
三维模型驱动结果如图7所示,与计算结果一致。

图7 正向结果验证Fig.7 Test data for forward kinematics
3.2 逆向验证
逆向验证选用腕部偏置伸缩Pieper机器人在掘进机截割头组对焊接作业实例来说明。悬臂式掘进机是煤矿井下巷道掘进的核心关键装备[21-23],截割头是掘进机关键件之一。在截割头自动化组对焊接时先将齿座调整到位,然后将齿座伸至截割头体贴面,如图8所示。

图8 掘进机截割头组对焊接Fig.8 Application in welding of cutting head
图8连杆尖点A(a,b,c)坐标为(-507.406 3,89.807 9,69.440 2),θx为20°,θy为-15°,θz为25°,位姿矩阵为

计算可得
(D0x,D0y,D0z)=(-367.338 1,155.122 8,110.851 2)
(E0x,E0y,E0z)=(-359.370 7,198.462 7,15.545 5)
(F0x,F0y,F0z)=(-284.959 5,233.161 2,37.545 2)
按照第2节所述方法编写程序,用时8 ms迭代7次得到计算结果为L6=-51.556,θ5=62.246 2°,逐步归位,由式(12)、式(15)得θ1=-35.595 4°,θ2=2.728 9°,θ3=22.539 2°,θ4=7.765 7°。
无论是在虚拟样机模拟还是在实体产品生产中,以上计算结果都极为精准。
3.3 产品应用
中国矿业大学(北京)与石家庄煤矿机械有限责任公司合作研发的新构型凿岩机器人采用腕部偏置伸缩Pieper构型,如图9所示。
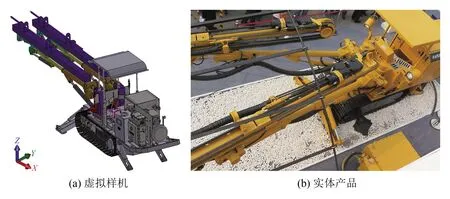
图9 凿岩机器人虚拟样机和产品Fig.9 Virtual prototype and product of rock drilling robot
目前对凿岩机器人进行了地面厂内试验,如图10所示。首先构建模拟巷道及前端工作面,按照兖矿集团东滩煤矿提供的86孔打眼数据在工作面上标出各孔位置,将各孔数据输入凿岩机器人;然后,进行地面试验,机器人自行完成各孔定位。

图10 凿岩机器人地面试验Fig.10 Drilling robot in ground test
地面试验所得实际定位结果与理论定位结果偏移量如图11所示。由图11可知,最大偏移为27.6 mm。凿岩机器人定位精准快速,符合矿方±30 mm打眼误差的要求。
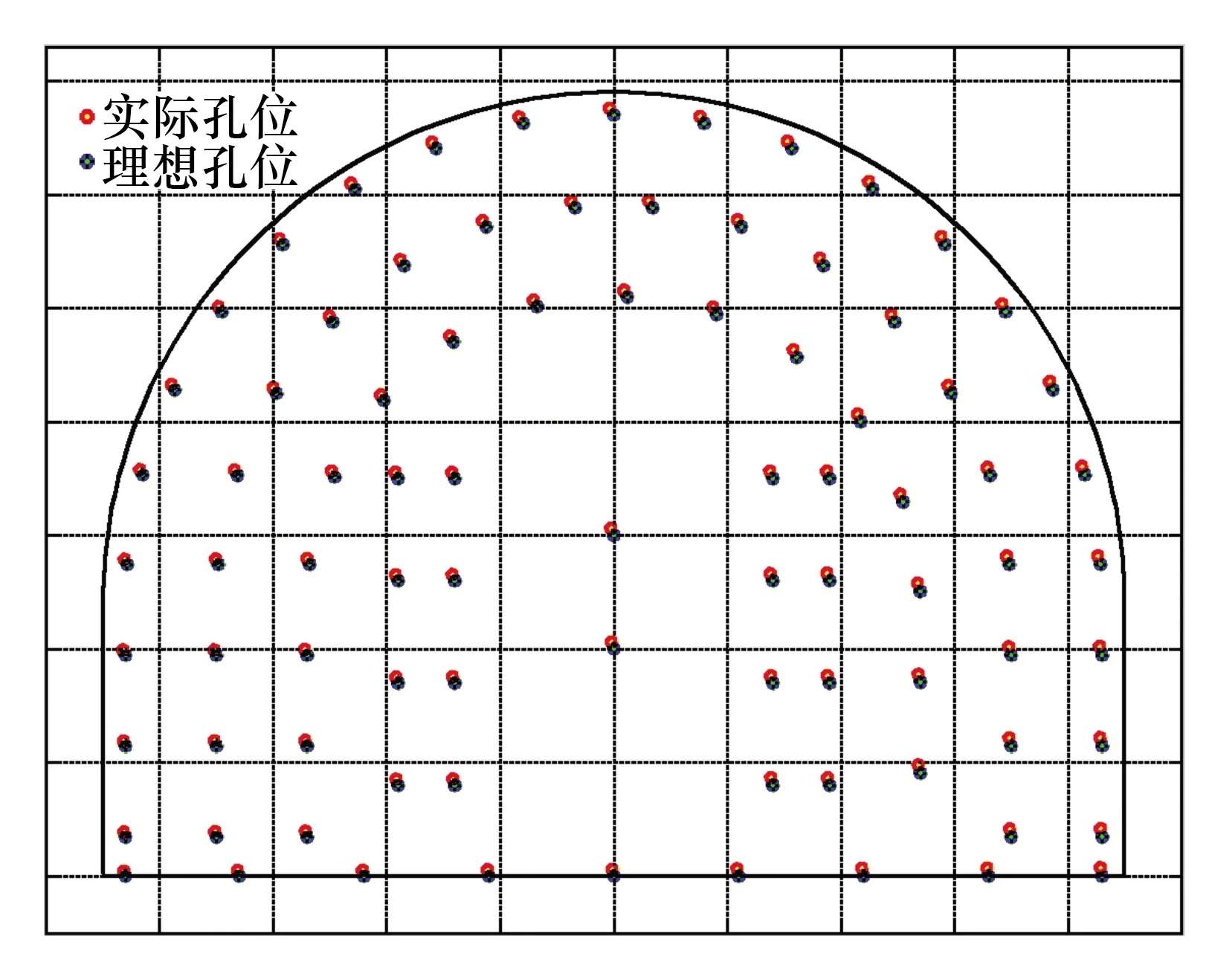
图11 加工和装配造成的定位误差Fig.11 Positioning error caused by machining and assembly
4 结 论
(1) 腕部偏置伸缩Pieper机器人采用偏置形式具有更强的结构刚度和更高的灵活性,动件6的伸缩使其有更好的应用性。
(2) 腕部偏置伸缩Pieper机器人存在3个两两相交矢量轴,可以实现逆向求解,由于腕部除了偏置还带有伸缩动作,其求解需要采用迭代搜索的求解形式。
(3) 腕部偏置伸缩Pieper机器人结构有2个特性:一是对第5自由度的求解可以转化为对特定直线与特定平面法线之间夹角的求解;二是矢量轴3和矢量轴4绕轴交点与原点O的距离为定值。这2个特性表明可以对第5和第6自由度进行迭代搜索求解。
(4) 数据结果显示迭代搜索过程仅迭代7或8次,耗时10 ms,精度误差可达10-8,求解准确、快速、简便。
(5) 基于全局坐标系内机器人空间状态关系的算法耗时短、精度高,解决了传统数值算法计算量大、耗时长且精度差的缺点,推动了腕部偏置伸缩Pieper构型在截割头组对焊接机器人及井下凿岩机器人等多种设备上的应用。地面试验表明,打眼误差在±30 mm内,效果良好,可满足精准和快速要求。
致谢:本课题得到了石家庄煤矿机械有限责任公司的大力支持,在此深表感谢!

