基于结构加权低秩近似的泊松图像去模糊

吴庆波，任文琦，*

（1.中国科学院信息工程研究所 信息安全国家重点实验室，北京 100193；2.中国科学院大学 网络空间安全学院，北京 100049）

当今，视频监控技术在社会治安管理中起着非常重要的作用，尤其是在夜间等人们不常活动的时间段。然而，成像设备固有的点扩散效应往往导致视频帧（或图像）中存在不同程度的模糊。同时，夜间有限的光照又不可避免地在图像中引起泊松噪声污染。这些因素通常会降低原始图像的质量，造成图像结构信息受损，给后续图像水印和图像取证等任务［1-3］增加了困难。因此，如何有效地从泊松图像中去除模糊和抑制噪声已经成为图像处理领域的重要研究课题。

为从泊松图像中去除模糊，现有工作［4-5］把降质图像的形成过程表示为数学模型：y=（Hx），y、x、H和分别为观测图像、清晰图像、模糊核和泊松噪声添加算子。因此，泊松图像去模糊问题归结为从观测图像y中恢复出清晰图像x，这是一个典型的不适定问题。为克服问题的不适定性，大部分泊松图像去模糊方法［6-10］建立在变分模型的基础上，先用正则化理论将不适定问题转化为适定问题，再借助优化技术恢复清晰图像。相关工作中的模型可以概括为：minxD（x，y）+R（x），函数D（x，y）和R（x）分别为数据项（Data Term）和正则项（Regularization Term）。数据项D（x，y）用于约束复原图像的内容与观测图像接近，防止恢复结果失真，主要来自泊松概率密度函数［11］：n为模糊图像中像素的索引，［Hx］n和yn分别为向量Hx和y中的第n个元素。正则项R（x）通常基于某种先验假设对清晰图像进行惩罚，以克服逆问题的不适定性，所以在很大程度上依赖于人们对清晰图像的先验知识（如平滑和低秩）。

现有泊松图像去模糊方法［12-16］基于不同的先验知识引入了多种正则项。Harmany等［13］假设清晰图像是平滑的，在正则项中使用全变分（Total Variation，TV）［17］抑制泊松噪声。全变分方法虽然能够保持物体的主要边缘，但在非平滑区域表现不佳，往往导致恢复结果中纹理细节的过平滑。为避免全变分的缺陷，Chen［15］在小波域使用L1-范数约束清晰图像的小波系数（Wavelet Coefficients），虽然恢复结果中的纹理细节有所改善，但是该方法采用固定的字典，仍然会导致恢复结果中存在模糊细节。为进一步改进去模糊结果的质量，Ma等［14］通过字典学习（Dictionary Learning）［18］的方法从观测图像中获得与图像内容相适应的基元，并借助学习到的字典从泊松图像中去除模糊，但是该方法在字典学习阶段比较耗时。为克服该问题，Buades等［19］认为清晰图像具有非局部自相似性，并基于此假设提出了非局部均值（Nonlocal Means，NLM）方法，从输入图像中去除高斯噪声。随后，研究人员［20-21］基于相似图像块的低秩假设使用加权核范数最小化（WNNM）方法［20］去除加性高斯噪声。但是，这些方法［19-21］仅仅通过滑动（平移）窗口在正视角度下搜索相似图像块。然而，实际中获得的图像常常含有大量的透视场景［22］。因此，对候选图像块进行合适的变换可以在一定程度上避免现有方法在正视角度下搜索相似图像块的局限。

为得到更高质量的复原图像，本文提出了基于结构加权低秩近似的泊松图像去模糊模型。在该模型中，首先，引入结构变换（Structural Transformation，ST），通过增加候选图像块的相似性在透视场景中更好地利用图像的非局部自相似性。然后，构造新的目标函数，基于相似图像块的低秩假设在正则项中使用加权核范数（WNN）［20］对结构变换后的相似图像块进行惩罚，从而使模型在去除高斯模糊和泊松噪声的同时有利于保持物体的结构信息。由于本文模型是具有可分性的非光滑优化问题，提出使用半正定二次分裂（Half-Quadratic Splitting，HQS）方法有效地求解目标函数。相关工作［22-24］在图像去噪和超分辨任务中也使用了某些结构变换，但是所采用的两步策略相对简单。相反，本文方法建立在统一的目标函数上，并借助优化技术进行泊松图像去模糊。超分辨方法［25］在残差块（Residual Block）中嵌入空间特征变换（SFT），以避免SRMD方法［26］在输入端串联模糊核和图像引起的与图像无关的干扰。SFT只含有缩放和平移2种操作，而本文提出的结构变换组合了4种基本操作，以提供更相似的图像块。

1 结构变换

除了传统的平移操作（滑动窗口）［19-21］，本文引入另外4种基本操作，即旋转、缩放、剪切和翻折。给定某正方形候选图像块P（u，v，r），（u，v）为图像块中心点在整个图像上的坐标，r为图像块的半径。

对于以（u，v）为坐标中心的像素点（i，j）∈P（u，v，r），翻折操作定义为Fp·（i，j）T，i，j∈［-r，r］。Fp有以下5种情况：

式中：Fo表示无翻折操作。

剪切操作定义为

式中：Δi和Δj分别为i-和j-轴上的剪切量。

当Δi=Δj=0时，S（Δi，Δj）为无剪切操作。

旋转操作定义为

式中：0≤θ＜2π为旋转角度。特别地，θ=0意味着不进行旋转操作。

缩放操作定义为数量c＞0。当c＞1和c＜1时，该操作分别放大和缩小图像块。当c=1时，该操作保持原始图像块的大小和形状。

一般地，翻折操作只适用于具有对称性的正方形图像块，因此可以最先施加在图像块P（u，v，r）中的每个像素上。旋转操作能够作用于任何形状的图像块，故而可以最后执行。剪切操作适合放置在前两类操作的中间。鉴于此，本文通过有序地联合基本操作引入结构变换。

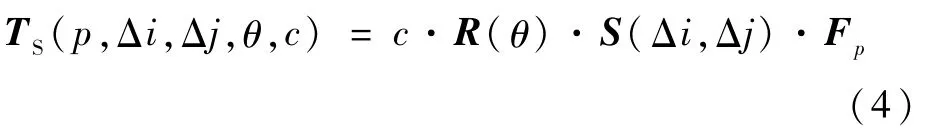
式中：p∈｛j=0，i=0，i=j，i=-j，o｝。对于参数p=o，Δi=Δj=θ=0和c=1，结构变换使原始图像块P（u，v，r）保持不变。为直观地说明结构变换的作用，对图1所示的参考图像块（r方框），用不同的方法搜索与其不同的相似图像块（s1、s2方框）。从图1（a）、（b）中可以看到，传统的滑动窗口方法产生的相似图像块（含参考图像块自身）有较大的秩（rank），而本文结构变换的结果有较小的秩。

图1 不同方法搜索相似图像块结果Fig.1 Results of sim ilar patches that are searched by differentmethods

2 泊松图像去模糊模型

为在透视场景中有效地去除模糊和抑制泊松噪声，考虑到相似图像块具有低秩性，在正则项R（x）中使用WNN［20］对结构变换后的相似图像块进行惩罚。基于此，构造新的目标函数如下：

式中：第一项和第二项分别为数据项和正则项；＜·，· ＞和λ＞0分别为内积运算符和超参数；1为元素都是1的列向量；矩阵含有k列，为图像块xn的k个相似图像块经结构变换后的列向量，WNN定义为

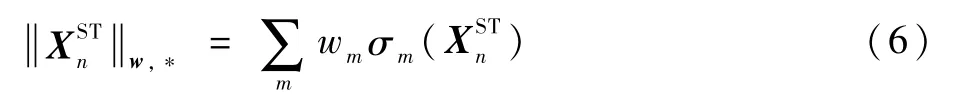
其中：σm为矩阵的第m个奇异值；wm为权重向量w的第m个元素。

此外，式（5）与相关工作［20］中的目标函数有以下2点区别：①文献［20］中的任务是去除加性高斯噪声，所以其目标函数可以建立在图像块的基础上；而本文的任务是去除高斯模糊，故而式（5）只能建立在整幅图像上。②文献［20］把相似图像块的搜索方式限制为平移操作，而式（5）因含有结构变换而更适用于恢复含透视场景的图像。

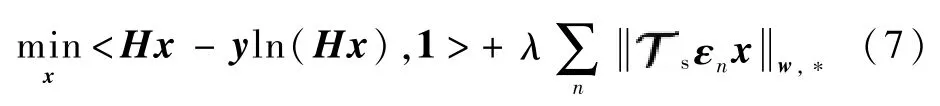
式中：算子εn的作用是从清晰图像x中提取出与参考图像块xn最相似的k个正方形图像块；算子的作用与结构变换TS（p，Δi，Δj，θ，c）相同，可以对提取出的k个正方形图像块进行变形。

3 优化求解方案

由于式（7）不可微但具有可分性，基于HQS方法提出交替方向最小化（Alternating Direction Minim ization，ADM）方案，用于求解目标函数。

式（7）松弛化为

式中：h和Zn分别为辅助向量和辅助矩阵；α，β＞0为超参数。当α，β→∞时，式（8）收敛到式（7）。更新辅助矩阵Zn。固定式（7）中与Zn相关的项，得到如下子问题：

该问题类似于WNNM 方法［20］中的目标函数，其解可以通过变量替换求得。于是，式（8）有如下闭合解：

式中：（Sw（Σ））m，m=max（σ′m-wm，0），σ′m为矩阵Σ主对角线上的第m个元素，权重向量w中的第m个元素定义为wm=/（σ′m+10-16）；［U，Σ，SVD为奇异值分解（Singular Value Decomposition）。

式（10）为抑制泊松噪声的操作，即从较大（小）的奇异值σ′m中减去较小（大）的权重wm。需要指出的是，式（9）中第一项使用F-范数是合理的，因为图像块中的泊松噪声在局部区域可近似为高斯分布［27-28］。

更新辅助向量h。固定与h有关的项，式（8）可以简化为

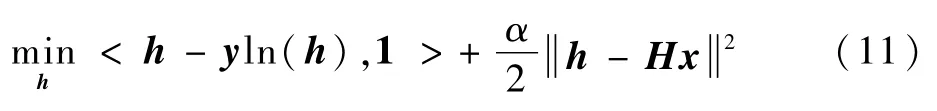
通过求导可获得问题（11）的闭合解：

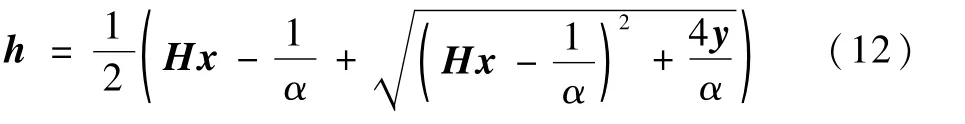
更新清晰图像x。固定式（8）中与x有关的项，得到如下子问题：

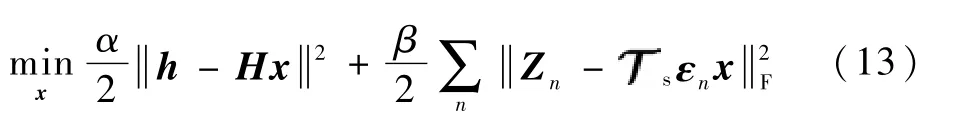
式（14）通过对去模糊图像HTh和无噪声图像块拼成的图像进行加权平均而恢复出清晰图像x。

综上所述，本文提出的基于结构加权低秩近似的泊松图像去模糊方法步骤如图2所示。

图2 基于结构加权低秩近似泊松图像去模糊方法流程Fig.2 Flowchart of structural weighted low-rank approximation method for Poisson image deblurring

步骤1输入含有泊松噪声的模糊图像y和模糊核H。

步骤2把清晰图像x初始化为输入图像y，置α=1.5，β=2。

步骤3对x中每一个图像块，搜索并存储k个最相似的图像块。

步骤4通过计算式（10）更新辅助矩阵Zn。

步骤5通过计算式（12）更新辅助向量h。

步骤6通过计算式（14）更新清晰图像x。

步骤7如果x的更新率（t为迭代次数）大于阈值10-5，转到步骤8。否则，输出清晰图像x。

步骤8如果t≤maxIter，把α和β乘以2后转到步骤3。否则，输出清晰图像x。

4 实验结果与分析

4.1 实验条件

由于本文主要考虑透视场景中的非局部自相似性，故在量化评估实验中选取如图3所示的20幅图像作为测试图像。其中，前两行的10幅自然图像［28］含有三维真实场景的透视结构，后两行的10幅生物医学图像中不仅存在一定程度的透视结构，还含有细微的边缘信息和纹理细节（http：//cellimagelibrary.org/）。

图3 量化评估中的20张测试图像Fig.3 Twenty test images for quantitative evaluation

为验证本文方法在泊松图像去模糊中的有效性，选用当前最新的方法［6-9］作为比较对象，也比较了本文方法不含结构变换时的情形。PURELET［8］采用一种端到端的线性框架，其反卷积过程为基函数的线性组合，因此该方法相当于求解线性系统。文献［6-7，9］方法与本文方法类似，也基于迭代方案对泊松图像去模糊。特别地，Hess［6］和PDS［7］采用了非局部自相似性先验，但是这些方法仅仅在滑动窗口中搜索与参考图像块最相似的k个图像块。本文方法不含结构变换时的情形可视为改造后用于泊松图像去模糊的WNNM方法。此外，由于基于深度网络的方法需要大量的训练数据，而这些数据通常较难获取［29］，目前还没有发现基于深度学习的泊松图像去模糊方法。

本文方法中的关键参数设置如下：①结构变换TS（p，Δi，Δj，θ，c）中的参数，p∈｛j=0，i=0，o｝，Δi，Δj∈｛-0.2，0，0.2｝，θ∈｛0，π/2，π，3π/2｝，c∈｛0.8，0.9，1，1.1，1.25｝；②对于泊松噪声峰值63、127、255、511和1 023，迭代次数分别设置为14、14、12、10和8，相应的超参数λ分别为0.024、0.02、0.018、0.014和0.01；③图像块的大小和相似图像块的个数分别设置为7×7和60。

为评估不同方法的性能，使用客观评价和主观评价2种方法比较去模糊结果的质量。在客观评价时，选用峰值信噪比（PSNR）和结构相似性（SSIM）作为度量指标。一般地，指标的值越大，复原图像的质量越高。所有实验都在配置为2.4 GHz Core i7 CPU和32 GB RAM 的机器上完成。

4.2 模型参数讨论

本文方法主要包含以下参数：式（4）中的翻折操作类型p、剪切操作在i-和j-轴上的偏移量Δi和Δj、旋转角度θ、缩放量c及式（5）中的超参数λ。式（4）中参数的量化粗细度对本文方法抑制泊松噪声的性能有较大影响。如果式（4）中参数的量化越细，那么候选图像块的数量越多。相应地，前k个相似图像块的相似度越大。对较大的奇异值，权重wm就越小，从而相应向量（表示物体边缘等主要信息）被越多地保留。对较小的奇异值，相应向量（表示噪声等次要信息）被越多地约减，所以方法的去噪性能越强。相反，如果式（4）中参数的量化越粗，方法的去噪性能越低。从图4（a）中的曲线可以看出，PSNR随着旋转角度间隔Δθ的减小而增加。当Δθ=π/2时，PSNR接近最大值，并且趋于平稳。据此，旋转角度的值设置为θ∈｛0，π/2，π，3π/2｝。此外，用该方法确定式（4）中其他参数的量化值。

式（5）中超参数λ的作用是调节正则项的重要性，其值严重地影响去模糊结果的质量。如果λ的取值偏小，数据项起主导作用，那么恢复的清晰图像与输入图像y更接近，所以往往含有较多的模糊和噪声。相反，如果λ的取值偏大，正则项起主要作用，那么复原结果中的边缘信息通常会被过度平滑。如图4（b）所示，对不同强度的泊松噪声，较小和较大的λ值都导致了较低的PSNR。但是平稳的曲线也表明，本文方法对参数λ的取值具有较强的鲁棒性。因此，对泊松噪声峰值63、127、255、511和1 023，超参数λ分别设置为0.024、0.02、0.018、0.014和0.01。

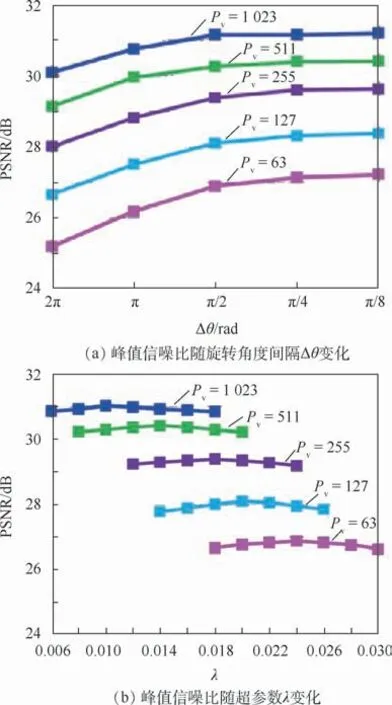
图4 峰值信噪比随旋转角度间隔Δθ和超参数λ变化的曲线Fig.4 Variation of PSNR with rotation intervalΔθand hyper-parameterλ

为验证本文方法对模糊程度和噪声水平的鲁棒性，选用图3中的第5幅图像作为测试图像。在合成模糊图像时，参数设置如下：模糊核的尺寸s和标准差σ分别置为（s，σ）=（7，2.5），（9，3）和（11，4），均值都为零，泊松噪声峰值分别为Pv=1023、511和255。用本文的默认参数从合成图像中恢复出图5中的清晰结果。随着噪声强度的增加，复原图像略微变暗，这主要是因为较小的泊松噪声峰值Pv（模拟实际中较暗的光照条件）增加了图像去模糊的难度。但是，第三列结果仍然含有比较明显的边缘信息。此外，随着模糊程度的增加，复原物体的纹理边缘丢失了少量信息，但是在整体上仍然比较锐利。

图5 本文方法对高斯模糊程度和泊松噪声水平的鲁棒性Fig.5 Robustness of proposed method to levels of Gaussian blur and Poisson noise

4.3 合成图像上的实验

1）非盲图像去模糊。为验证本文方法恢复透视场景细节的性能，首先考虑高斯模糊核已知的情形，并选用图6（a）中的生物医学图像作为测试图像。该图像含有丰富的纹理细节，但细胞表面的细节受细胞球形结构的影响存在一定的形变。图6（b）中的合成图像含有泊松噪声，峰值为511，不同方法的去模糊结果如图6（c）～（h）所示。通过观察放大的细节可以发现，图6（c）中的细胞表面含有明显的噪声，主要因为PURE-LET方法［8］中的反卷积过程容易放大图像噪声。由于TGV方法［9］中的剪切波字典与图像内容无关，图6（d）中细胞表面的一些纹理细节因过平滑而丢失。虽然文献［6-7］也采用了非局部自相似性先验，但是图6（e）、（f）中的细胞都有严重的模糊伪影，因为这2种方法在搜索相似图像块时仅仅限于正视角度。本文方法如果在结构变换中使用保持原图像块的参数设置，也会产生类似的模糊效果，如图6（g）所示。相反，本文方法在式（4）中使用更多的参数量化时产生了图6（h）中锐利的纹理信息。表明本文方法在恢复透视场景细节方面优于当前最新的同类方法［6-9］。

图6 非盲图像去模糊中不同方法的比较Fig.6 Comparison of differentmethods in non-blind image deblurring

为进一步验证本文方法的有效性，利用图3中的20幅图像进行更多的非盲图像去模糊实验，并使用mPSNR和mSSIM作为定量评价指标，表1给出了不同方法在测试图像上的平均统计结果。考虑到噪声强度对方法性能的影响，表1也包括了3个典型的泊松噪声峰值，即63、255和1 023。可以看到，在自然图像和医学图像上，本文方法、Hess［6］、PDS［7］和TGV［9］的mPSNR都高于PURELET［8］。这主要是因为前4种方法都基于正则化理论和迭代优化方案，能够有效地抑制泊松噪声；而PURE-LET使用端到端的线性框架，对图像中的乘性噪声比较敏感。虽然Hess［6］、PDS［7］和TGV［9］产生了更高的mPSNR，但是增量比较有限。原因主要是：TGV［9］中的剪切波是固定的，不能有效地表示图像中的纹理细节，而PDS［7］和Hess［6］都只在正视角度下搜索相似图像块。相反，对各种强度的泊松噪声，本文方法在使用结构变换时取得的mPSNR和mSSIM都明显地高于当前最新的去模糊方法［6-9］。这主要得益于结构变换增加了搜索空间中候选图像块的相似性，从而有利于保持图像内容中的主要信息和约减次要信息。

表1 非盲图像去模糊中多种泊松噪声强度下不同方法恢复结果的平均峰值信噪比和结构相似性Tab le 1 M ean PSNR and SSIM of results recovered by d ifferentm ethods on test im ages w ith various intensities of Poisson noise in non-b lind im age deb lur ring

2）盲图像去模糊。通常情况下，模糊核是未知的，所以在去模糊之前需要对模糊核进行估计。为验证本文方法对模糊核估计的鲁棒性，在合成数据上进行盲图像去模糊实验。为此，首先选用图7（a）所示的模糊核作为真值，图7（c）中含有对称结构的自然图像作为测试图像。按照4.1节的方法，利用这些数据生成含有峰值为511的泊松噪声模糊图像，如图7（d）所示。使用文献［30］中的方法从模糊图像中估计模糊核，如图7（b）所示。把估计的模糊核输入到不同的去模糊方法［6，8-9］中，得到图7（e）～（h）所示的恢复结果。

从图7（e）可以看出，蝴蝶的左翼含有明显的噪声，因为PURE-LET方法［8］中反卷积过程使用了线性维纳滤波（W iener Filtering），容易放大乘性泊松噪声。图7（f）中的去模糊结果有明显的过平滑现象，主要原因是TGV方法［9］使用固定的剪切波作为基函数，以致表示细节的能力十分有限。从图7（g）中可以看出，虽然Hess方法［6］显著地改善了纹理细节，但是恢复结果中的边缘信息仍然不够清晰。相反，本文方法恢复出了图7（h）中更加锐利的结构信息，所以明显地优于当前最新的去模糊方法［6，8-9］。需要注意，这些结果的复原都基于图7（b）中估计的模糊核。因此，实验结果表明了本文方法在盲图像去模糊中对估计的模糊核有较强的鲁棒。

图7 盲图像去模糊中不同方法的比较Fig.7 Comparison of differentmethods in blind image deblurring

4.4 结构变换的有效性

结构变换在本文方法中起着重要的作用。为进一步验证结构变换的有效性，首先，根据透视程度把图3中的自然图像划分成3组：第1组为轻微透视图像，包含图3中第9和第10幅图像；第2组为中等透视图像，由图3中第6～第8幅图像组成；第3组为明显透视图像，包括图3中的第1～第5幅图像。然后，按照4.1节的方法合成3组模糊图像，泊松噪声峰值均为511。最后，使用包含和不含结构变换的本文方法对3组退化图像进行非盲去模糊，并计算每组结果的mPSNR。为表明结构变换的作用，进一步计算本文方法对不含结构变换时mPSNR 的增量。如图8所示，本文方法在轻微透视图像上取得了较小的mPSNR增量，而在明显透视图像上取得了较大的mPSNR增量。表明本文提出的结构变换有利于从透视结构显著的泊松图像中去除模糊。

图8 结构变换的有效性Fig.8 Effectiveness of structural transformation

4.5 真实图像上的实验

本文方法在合成图像上取得了较好的效果，为验证其在真实图像上的泛化性能，使用图9（b）所示的生物医学图像（http：//cellimagelibrary.org/）进行更多的实验。对比方法选用端到端的PURE-LET［8］和基于变分模型的Hess［6］。在实验中，首先采用文献［30］中的方法，从真实图像中估计出模糊核，如图9（a）所示。然后，把这些估计的模糊核输入到不同的去模糊方法中，得到最终的清晰图像。从图9（c）可以看出，PURE-LET方法［8］能够有效地去除图像模糊、增强纹理细节，但也往往导致图像噪声放大，因为反卷积过程是一个端到端的线性框架，对噪声比较敏感。相反，由于Hess方法［6］中的基函数与图像内容无关，图9（d）中的纹理细节被过度平滑。从图9（e）可以观察到，本文方法成功地去除了高斯模糊和泊松噪声，同时也保留了锐利的边缘信息和纹理细节。这主要得益于结构变换提供了更相似的图像块，使得式（10）中较大奇异值减去较小的权重，相应向量能保留更多的边缘信息。

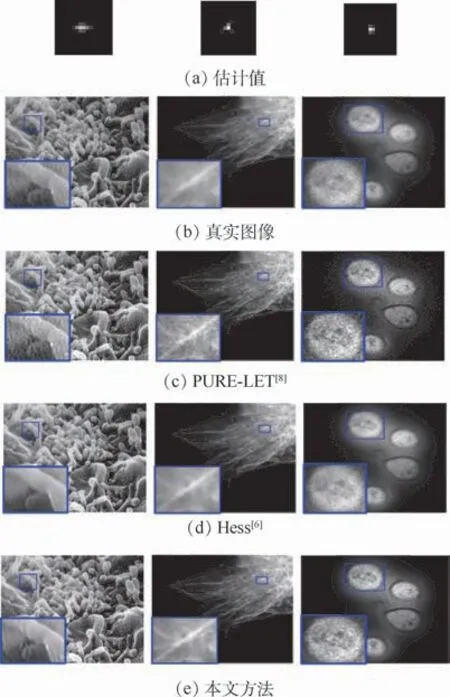
图9 真实图像去模糊中不同方法的比较Fig.9 Comparison of differentmethods on real-world image deblurring

5 结 论

针对泊松噪声图像去模糊问题，提出了基于结构加权低秩近似的图像去模糊方法。该方法具有以下优势：

1）充分考虑了图像内容的透视结构。引入的结构变换有利于增加搜索空间中相似图像块的相似性，从而改进了非局部自相似性在透视场景中的适用性。

2）可用于无训练样本或者训练量样本量较少的观测数据，如生物医学图像，也可拓展到夜间和背光情形下的高斯模糊图像。

实验表明，本文方法明显优于当前最新的泊松图像去模糊方法，特别是在透视结构显著的图像上。在图像去模糊过程中，抑制泊松噪声放大的关键是通过从较大（小）的奇异值减去较小（大）的权重。如果结构变换的参数量化地越细，与较大奇异值对应的权重就越小，从而在去除高斯模糊和抑制泊松噪声的同时能够有效地保持边缘信息和纹理细节。但是，这也会导致相似图像块的搜索需要更长的时间。此外，奇异值分解过程也需要时间。鉴于此，下一步工作的重点是通过探索新的搜索策略和奇异值估计方法提高本文去模糊方法的执行效率。