双轴载荷下复合材料开口强度分析与试验方法研究
熊美蓉,陈琳,张达,刘传军
(1.中国商飞上海飞机制造有限公司,复合材料中心,上海 200123;2.中国商飞北京民用飞机技术研究中心,民用飞机结构与复合材料北京市重点实验室,北京 102211)
0 引言
复合材料开口产生的局部应力集中会引起结构强度下降,其应力集中水平与层压板铺层比例、载荷情况、缺口尺寸和形状以及缺口约束情况有关。
对于单轴载荷下复合材料开口结构,可采用基于断裂力学模型Mar-Lin准则[1]进行开口层合板剩余强度分析。将开口定义为损伤,通过获得不同铺层下的复合材料断裂韧性、奇异性参数、构型因子等,拟合得到不同开口尺寸下的层合板剩余强度;另一种方法是采用基于应力失效模型的Withney-Nuismer[2]方法,获得圆孔层合板在圆孔中心线上垂直于远场载荷方向的应力分布,再通过点应力或平均应力方法开展失效分析。
而对于复合材料在双轴载荷下的开口强度分析,Lehknitskii理论(解析法)[3]中提出可利用复变函数计算含椭圆孔(圆孔)的正交各向异性无限大板在复杂远场载荷作用下的孔边应力分布。但目前缺少对该方法的试验验证和标准的试验方法。A.Makris[4]总结了几种公开报道的复合材料双轴试验方法,可采用单个加载系统或多个独立加载系统实现多向应力状态,并认为需仔细评估试验件构型以获得合理的失效模式。A.Smits[5]设计了不同倒角的十字型复合材料双轴试验件,研究不同加载比例下试验件应力分布和失效模式。DanielI.M.[6-7]采用八边形试验件对复合材料开口结构开展双轴载荷试验,试验结果与平均应力失效准则和单层渐进失效模型预测结果具有较高的一致性。
本文主要针对T800级碳纤维复合材料层合板开口结构,对双轴载荷下复合材料开口强度方法进行研究,并设计开口结构的双轴载荷试验,以对分析方法进行验证。
1 复杂应力开口分析方法
对于无限大的复合材料各向异性层合板开口结构,Lehknitskii理论[2]中提出的复变函数可用于计算含椭圆孔(圆孔)的正交各向异性无限大板在复杂远场载荷作用下的开口边缘应力分布。考虑到对复合材料开口层合板上施加双向载荷时,难以在开口周围获得均匀的远场应力,因此无法满足Lehknitskii理论的基本假设。本节拟采用有限元方法与Lehknitskii方法进行对比,分析该方法的适用性和准确性,同时验证有限元模型。
1.1 Lehknitskii方法
Lehknitskii模型如图1所示。分析假设如下:
(a)材料主轴方向1、2与椭圆孔主轴方向x、y一致。
(b)平板尺寸与椭圆孔或者圆孔尺寸相比可认为是无限大。
(d)考虑平面应变或者广义平面应力情形。

图1 在远场应力作用下、含开口的无限大平板
孔缘的应力由远场应力和扰动应力构成,计算式如下:







由于孔存在产生的扰动项形式可通过如下方式计算:
式中:Re——复数的实部;
Zk——复数变量,Zk=x+yμk(k=1,2);

Φk(Zk)为复应力函数,由椭圆孔存在引起的扰动应力对应的应力函数为:
1.2 有限元法
通过Abaqus有限元软件,可建立复合材料开口层合板结构有限元模型,进而计算出孔周围应力分布。开口部分采用以4节点四边形单元进行建模,考虑到孔边为复杂应力区,应力梯度较大,因此在模型中将孔边三圈网格大小设置为0.5 mm,往外网格密度变大,网格大小在1 mm。
图2所示为准各向同性铺层层合板在双轴载荷下的开口边缘最大应变的分布云图。从图2中可知,开口边缘最大主应变为3 466 με,而采用Lehknitski公式计算得到最大应变为3 458 με,与解析法计算的最大应变相差9 με,偏差在0.26%。可以看出,解析法和有限元分析方法分析结果非常一致,解析解和数值解的对比验证了开口区应力分析方法的准确性。

图2 复合材料开口试验件有限元模型和最大主应变分布云图
2 开口双轴试验方法
为对复合材料开口分析方法进行进一步验证,本文开展了复合材料开口结构的双轴载荷验证试验。考虑目前尚无可供参考的标准试验方法对复合材料开口结构的复杂应力状态进行测试和研究,本文参考文献中试验件构型,并根据数值模拟优化几何参数,设计了“十字型”复合材料开口试验件,以开展双轴拉伸试验,得到复杂应力下不同铺层开口结构在不同加载比例下的应力分布,进一步验证有限元模型及失效分析方法。
试验件采用T800级碳纤维复合材料,层合板0 °/±45 °/90 °的铺层比例为60%/30%/10%,试验件中心开圆形孔,直径为25.4 mm。十字型试验件在四个夹持端均带有加强片,且在十字转角处设计大曲率R区均匀过度,以减小应力集中,确保破坏模式正确有效,试验件构型如图3(a)所示。
双轴载荷试验采用INSTRON公司的DYNS多轴试验机,试验机双轴包括A轴和B轴。试验过程中,开口试验件0 °沿试验机B轴进行夹持,90 °方向沿试验机A轴进行夹持,试验件夹持深度为50 mm。双轴加载中偏小载荷加载轴加载速率为0.3 kN/s,数采频率为20 Hz。为更好分析试验件失效,试验过程中采用非接触应变测量系统对试验件破坏全过程进行高速采集,如图3(b)所示。

图3 双轴开口试验件示意图和双轴试验系统
3 试验结果分析
3.1 应力应变分析

图4 双轴试验件的应变-X轴加载载荷分布曲线
对铺层比例为[60%/30%/10%]的复合材料开口层合板在双轴载荷下的试验数据进行分析,图4为开口试验件两个典型位置的应变—载荷变化曲线,纵坐标为孔边应变与远场应变的比值。可以看出,远端应变与孔边应变先随载荷增长线性增加,比值恒定。当X轴载荷超过80kN后,应变比值出现波动,主要原因为试验件孔边出现局部损伤,继续加载到一定载荷,试验件发生破坏。
取试验加载过程中任一载荷水平下分析开口边缘应变分布情况,应变片分布如图3(a)所示,从孔边布置的8个应变片数据可以看出,试验件±45 °轴线上的应变相对0/90 °轴线较大(表1)。与采用Lehknitskii模型分析的孔边应力分布趋势一致,由图5中可知,当复合材料开口层合板在X轴 ∶Y轴远场应力比为2 ∶1时,开口边缘最大主应力出现在55 °、125 °、235 °和305 °方向上,应变分布趋势与试验结果一致。

表1 双轴试验件开口边缘切向应变数据
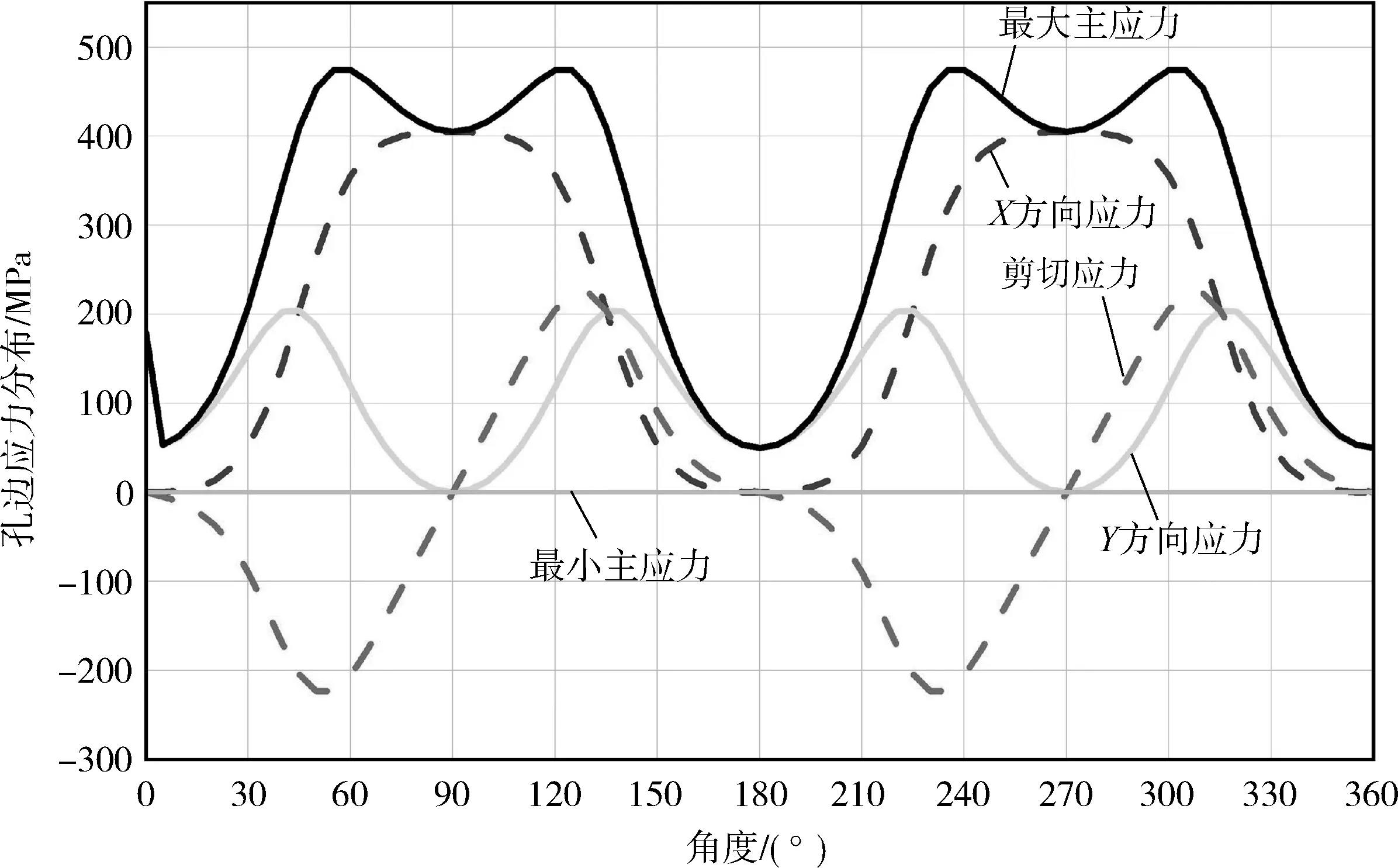
图5 X轴与Y轴加载比例为2 ∶1时,631铺层复合材料开口边缘应力应变分布
3.2 有限元对比分析
采用Abaqus对“十字型”复合材料开口试验件构型进行了有限元建模分析,模型示意图如图6所示。根据对点应力参数特征长度d0的分析,对开口直径为25.4 mm的层合板在拉伸载荷下,铺层比例对d0的影响较小。根据前期试验结果,在[60/40/10]~[40/50/10]铺层比例范围内,在拉伸载荷下特征长度d0可取2 mm。因此,在试验件有限元模型中,在网格划分时,确保孔边第二圈网格单元的中心距离边缘为2 mm,以用于后续开展开口边缘失效分析。

图6 复合材料开口双轴试验件有限元模型
图7中对比了开口边缘不同角度应变以及等直段应变与有限元分析结果。其数据表明,应变一致性较好,应变数据偏差在10%范围内,较好地验证了应力分析方法。引起偏差的原因可能是应变片粘贴的位置误差,因层合板开口区周围应变梯度较大,部分应变与模型会有一定偏离。

图7 开口边缘冲击后压缩许用值与开口尺寸的关系
3.3 失效分析
对于复合材料层压板应力集中的强度分析,可采用“点应力准则”作为复合材料层合板的失效判据。该准则为距离孔边某一特征长度d0处的层合板平均应力达到层合板无缺口许用应力时,层压板发生破坏。
由已有数据可知,对于试验件铺层且开口直径为25.4 mm的层合板拉伸特征距离d0为2.0 mm,根据有限元模型和求解结果可知,第二圈网格单元中心离孔边为2.0 mm,根据“点应力准则”,当第二圈单元最大应力达到无缺口许用应力时,试验件破坏,可获得试验件预测破坏载荷为144 kN,与试验的平均破坏载荷值141 kN接近,可以看出,双轴载荷试验数据与预测破坏载荷一致性较高。
从失效模式来看,试验件最终破坏形式如图8所示。试验件破坏主要出现在开口周围和四个圆弧区,与有限元模型的应力分布对比,最大应力位置分布也基本一致,因此失效模式与有限元模型分析结果接近(图9)。

图8 开口试验件破坏后形貌

图9 开口试验件有限元应力分布云图
试验过程中采用非接触测量系统对试验件加载过程进行监测,如图10(a)中所示,监测点3和点4在最早出现了应变的急剧增加,而后随着继续加载,其他监测点0、点1和点2应变急剧增加,试验件破坏。从监测结果判断,试验件在加载过程中,两轴的大曲率R区和中心开口边缘同时出现应力集中,试验件产生局部裂纹,试验件继续承载,当试验件最大应力点达到无缺口许用应力时,试验件发生整体破坏。与有限元应变分布云图对比,复合材料开口双轴载荷试验应变分布与数值计算结果基本一致,如图10(b)所示。
从试验结果看出,尽管在设计“十字型”复合材料开口双轴试验件时,已考虑采用大曲率降低四个R区的应力集中,避免孔边失效前出现其他失效模式。但实际试验件加工过程中,R区的加工误差和精度均有可能增加应力集中程度。因此,在后续开口双轴试验件设计时,可采用增加加强片的方法确保R区不会提前发生破坏。

图10 非接触测量结果与有限元应变分布云图
4 结论
本文中主要针对T800级碳纤维复合材料层合板开口结构,开展双轴载荷下开口强度分析与试验方法研究,通过对比分析,得出以下结论:
(1)采用Lehknitskii模型分析复合材料开口结构在双轴载荷的应力应变分布与有限元结果一致性较好,在已知远场载荷时可准确分析出开口边缘最大应力应变分布。
(2)双轴试验采用“十字型”复合材料开口试验件进行加载,试验件远端和开口边缘的应变分布与数值结果对比,误差在10%以内,且采用“点应力准则”预测的试验件破坏载荷与试验平均载荷值接近。
(3)通过对双轴载荷下试验件破坏过程进行监测,在试验件X轴与Y轴的大曲率R区位置提前出现了应力集中和局部破坏,建议在后续试验件设计时在R区增加加强片,以减少对孔边破坏的影响,确保试验件失效模式正确。

