“数据的分析”单元测试题(A)
蔡田雨

一、选择题(每小题3分,共30分)
1.为了解某校八年级800名学生数学期中考试情况,从中抽取了200名学生的成绩进行统计.现有下列判断:①这种调查方式是抽样调查;②800名学生是总体;③每名学生的数学期中考试成绩是个体;④200名学生是总体的一个样本;⑤200名学生是样本容量.其中正确的判断有( ).
A.1个 B.2个 C.3个 D.4个
2.甲、乙两班学生人数相同.在同一次数学单元测试中,两班成绩的平均分和方差分别如下:x甲=x乙=80分;s甲=240,s乙=180.则成绩较为稳定的班级是( ).
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
3.某地连续9天的最高气温统计如下:
这组数据的中位数和众数分别是( ).
A. 24℃. 25℃ B.24.5℃C. 25℃
C.25℃.24℃ D.23.5℃.24℃
4.学校对学生进行晨检体温测量.学生甲连续10天的体温(单位:℃)与36CC的上下波动数据为0.2,0.3,0.1,0.1,O,0.2,0.1,0.1,0,0.1,则在这10天中该生的体温波动数据中不正确的是( ).
A.平均数为0.12℃.众数为0.1℃
C.中位数为0.1℃ D.方差为0.02℃
5.甲、乙、丙、丁四人的数学测验成绩分别为90分、90分、x分、80分.若这组数据的众数与平均数恰好相等,则这组数据的中位数是( ).
A.100分B.95分C.90分D.85分
6.已知某班35人身高的算术平均数是158 cm.但后来发现其中有位同学的身高登记错误,误将160 cm写成了166 cm.设正确的平均数为a cm.下面关于口的叙述中,正确的是( ).
A.大于158 B.小于158
C.等于158 D.无法确定
7.在样本方差的计算公式S2=1/10[ (x1=20)2+(x2-20)2+...+(xn-20)2]中,數字10和20分别表示这组数据的( ).
A.中位数和众数
B.平均数和众数
C.样本容量和样本平均数
D.方差和平均数
8.为筹备班级的初中毕业联欢会,班长对全班同学爱吃哪几种水果进行了民意调查,那么对于最终买什么水果,下面的调查数据中最值得关注的是( ).
A.众数 B.平均数
C.中位数 D.方差
9.已知一组数据1,2,),的平均数为4,那么( ).
A. y=7 B.y=8 C.y=9 D.y=10
10.若一组数据2a1,2a2,…,2an的方差是5,则数据a,a2,…,an的方差是( ).
A.5 B.10 c.5/2 D.5/4
二、填空题(每小题3分,共l5分)
11.数学期末总评成绩由作业分数、课堂参与分数、期考分数三部分组成,并按3:314的比例确定.已知小明的期考是80分,作业是90分,课堂参与是85分,则他的总评成绩为 ____ .
12.在一次测验中,某学习小组的5名学生的成绩(单位:分)如下:68,75,67,66,99.这组成绩的平均分x=____,中位数M=____,去掉一个最高分后的平均分x'=____ .那么所求的x,M,x'这三个数据中,你认为能描述该小组学生这次测验成绩一般水平的数据是____.
13.从一个班抽测了6名男生的身高(单位:cm),将测得的每一个数据都减去165.0,得到如下结果:
-1.2,O.l,-8.3,1.2,10.8,-7.0.
这6名男生中最高身高与最低身高的差是_____,这6名男生的平均身高约为____(结果保留到小数点后第一位).
14.图1是北京故宫博物院2018年国庆期间客流指数统计图(客流指数是指景区当日客流量与2018年10月1日客流量的比值).
根据图中信息,不考虑其他因素,如果小宇想在今年国庆期间游客较少时参观故宫,最好选择在10月____日参观.
15.甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计如下:
某同学分析上表后得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);③甲班成绩的波动比乙班大.上述结论中正确的是____(填序号).
三、解答题(共75分)
16.(6分)某校同学进行知识竞赛.将他们所得成绩进行整理后,得到图2.求竞赛成绩的平均数.
17.(_7分)物理老师布置了10道选择题作为课堂练习,图3是全班解题情况的统计.平均每个学生做对了几道题?并求做对题数的中位数,众数.
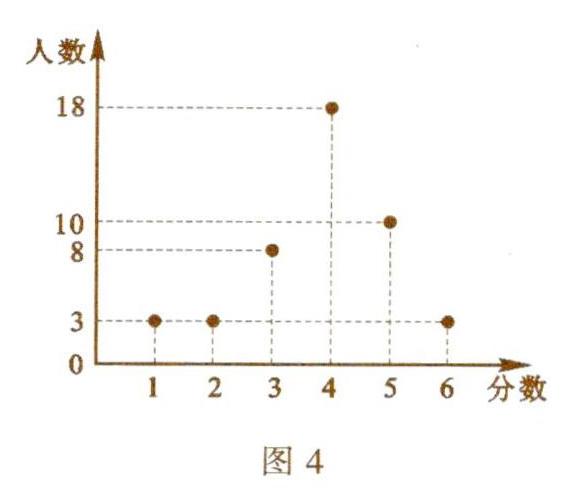
18.(8分)现有A,B两个班级,每个班级各有45名学生参加一次测试,每名参加者可获得0,1,2,3,4,5,6,7,8,9这几种不同分值中的一种A班的成绩如表3所示,B班的成绩如图4所示.
(1)观察可知____班的方差较大;
(2)若两班合计共有60人及格,参加者最少获 ____分才可以及格.
19.(10分)某工厂有220名员工.财务科要了解员工的收入情况,抽查了10名员工的本月收入(单位:元),结果如下:
1 660 1 540 1 510 1 670 1 620
1 580 1 580 1 600 1 620 1 620
(1)全廠员工的月平均收入是多少?
(2)平均每名员工的年薪是多少?
(3)财务科本月应准备多少钱发工资?
(4) 一名本月收人为1 570元的员工,他的收入水平如何?
*20.(10分)为迎接2022年冬奥会,鼓励更多的学生参与到志愿服务中来,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各400名学生进入综合素质展示环节.为了了解两所学校学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对成绩数据进行整理、描述和分析,下面给出了部分信息.
a.甲学校学生成绩的频数分布直方图如下(数据分成6组:40≤x<50,50 ≤x<60,60≤x<70,70≤x<80,80 ≤x<90,90≤x≤100):
b.甲学校学生成绩在80≤x<90这一组的情况是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
根据以上信息,回答下列问题:
(1)甲学校学生A,乙学校学生B的综合素质展示成绩同为83分,这两人在本校学生的综合素质展示成绩排名中更靠前的是____(填“A”或“B”).
(2)根据上述信息,推断 ____ 学校综合素质展示的水平更高,理由为____(至少从两个不同角度说明推断的合理性).
(3)若每所学校综合素质展示成绩的前120名学生将被选人志愿服务团队,预估甲学校分数至少达到____ 分的学生才可以入选.
*21(12分)某公司的午餐采用自助的形式,并倡导员工“适度取餐,减少浪费”,该公司共有10个部门,各部门的人数相同.为了解午餐的浪费情况,公司从这10个部门中随机抽取了A,B两个部门,进行连续四周
(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的质量,以下简称“每日餐余质量”(单位:kg),并对这些数据进行了整理、描述和分析.下面给出了部分信息.
a.A部门每日餐余质量的频数分布直方图如下(数据分成6.组:0≤x<2,2 ≤x<4,4≤x<6,6≤x<8, 8≤x<10, 10≤x≤12):
b.A部门每日餐余质量(单位:kg)在6≤x<8这一组的情况是:
6.1 6.6 7.0 7.0 7.0 7.8
c.B部门每日餐余质量(单位:kg)如下:
1.4 2.8 6.9 7.8 1.9
9.7 3.1 4.6 6.9 10.8
6.9 2.6 7.5 6.9 9.5
7.8 8.4 8.3 9.4 8.8
d.A.B两个部门这20个工作日每日餐余质量(单位:kg)的平均数、中位数、众数如下:
根据以上信息,回答下列问题:
(1)写出表中m,n的值;
(2)在A,B这两个部门中,“适度取餐,减少浪费”做得较好的部门是____(填“A”或“B”),理由是____;
(3)结合A,B这两个部门每日餐余质量的数据,估计该公司10个部门一年(按240个工作日计算)的餐余总质量.
22.(10分)某厂生产A,B两种产品,其单价随市场变化而相应调整.营销人员根据前三次单价变化的情况,绘制了如下的统计表(表6)及不完整的折线图(图7),并求得了A产品三次单价的平均数和方差:XA=5,9,s2=43/150.
(1)补全图7中B产品单价变化的折线图,计算可知,B产品第三次的单价比第二次的单价降低了____%.
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小.
(3)该厂决定第四次调价,A产品的单价仍为6.5元,B产品的单价比3元上调m%(m>0),使得A产品这四次单价的中位数比B产品这四次单价的中位数的2倍少1元.求m的值.
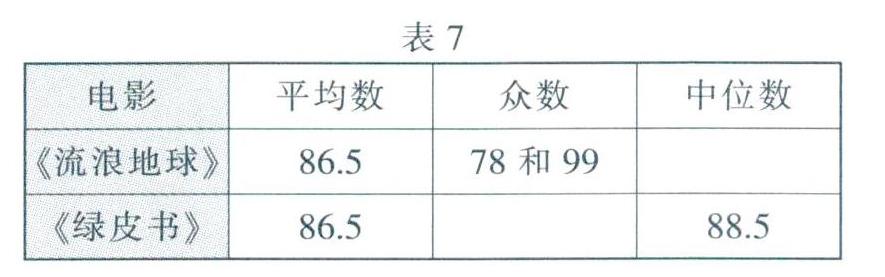
23.(12分)2019年初,电影《流浪地球》和《绿皮书》陆续热播.为了解某大学1800名学生对这两部电影的喜爱程度,调查小组随机抽取了该大学20名学生对两部电影打分,过程如下.
【收集数据】20名大学生对两部电影的打分结果如下,
《流浪地球》:
78 75 99 98 79 67 88 78 76 98
88 79 97 91 78 80 93 90 99 99
《绿皮书》:
88 79 68 97 85 74 96 84 92 97
89 81 91 75 80 85 91 89 97 92
【整理、描述数据】绘制了如下频数分布直方图和统计表,请补充完整.
(说明:60≤x<70表示一般喜欢,70≤x<80表示比较喜欢.80≤x<90表示喜欢,90≤x<100表示超级喜欢)
【分析数据、推断结论】
(1)估计该大学超级喜欢电影《绿皮书》的有 ____人;
(2)你认为观众更喜欢这两部电影中的____,理由是______.
(答案在本期找)
- 中学生数理化·八年级数学人教版的其它文章
- 方差变化规律揭秘
- 爱迪生的建议
- 数据的集中趋势和离散程度
- 分析集中趋势 把握波动程度
- 形式各异的权
- 学“三数”,用“三数”

