学会多角度进行评价

张青华

利用数据分析的结果，对所调查对象进行合理评价，是运用统计知识解决实际问题的核心.而由于评价的角度不同，得到的结论也不会相同.因此，如何多角度进行评价，成为考查学生数据分析能力的重要指标.在2019年的中考题中，出现了不少这方面的题目，让我们一起来研究一下吧！

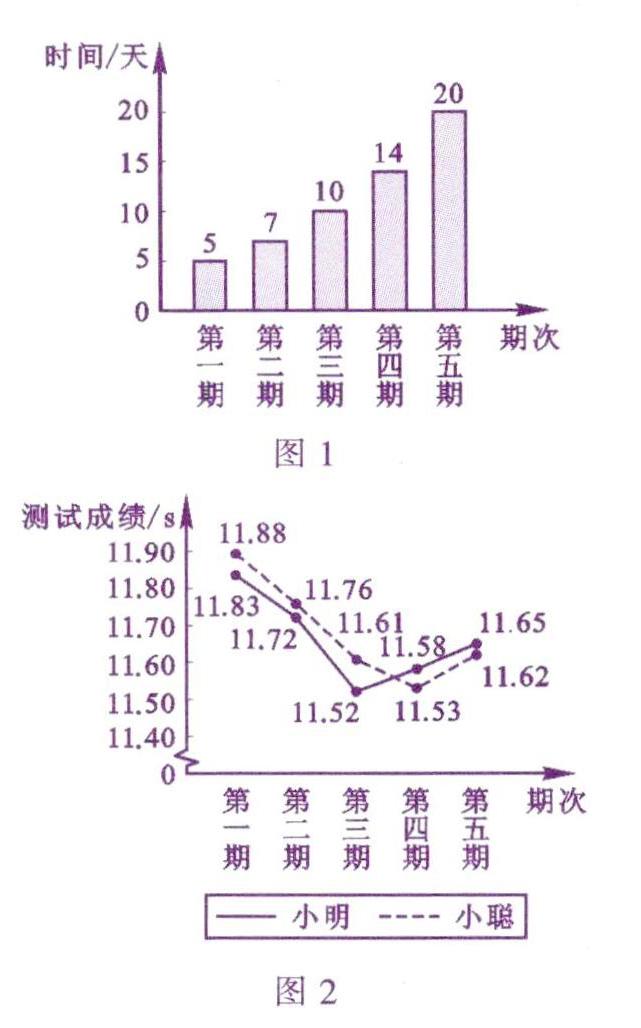
例1（2019年·绍兴）小明、小聪参加了100 m跑的5期集训，每期集训结束时进行测试，根据他们的集训时间和测试成绩，绘制了如下两个统计图.

根据图中信息，解答下列问题：

（1）這5期的集训共有多少天？小聪5次测试的平均成绩是多少秒？

（2）根据统计数据，结合体育运动的实际，从集训时间和测试成绩这两方面说说你的想法，

解：（1）这5期的集训共有5+7+10+14+20=56（天），小聪5次测试的平均成绩是（11.88+11.76+11.61+11.53+11.62）÷5=11.68 （s）.

（2）角度1：从集训时间看，集训时间不是越多越好，集训时间过长，可能造成劳累，导致成绩下滑，如图中第五期与前面两期相比，

角度2：从测试成绩看，两人的最好成绩分别是在第三期、第四期出现，建议将集训时间定为14天（同第四期的时间）.

角度3：集训时间每期都增加，测试成绩先上升后下降.

点评：对于（2）题，角度不同评价也不同，答案不唯一.

例2（2019年·嘉兴）在推进嘉兴市城乡生活垃圾分类的行动中，某社区为了解居民掌握垃圾分类知识的情况，进行了调查.A，B两小区分别有500名居民参加了测试.社区从中各随机抽取50名居民的成绩进行整理，得到如下部分信息：

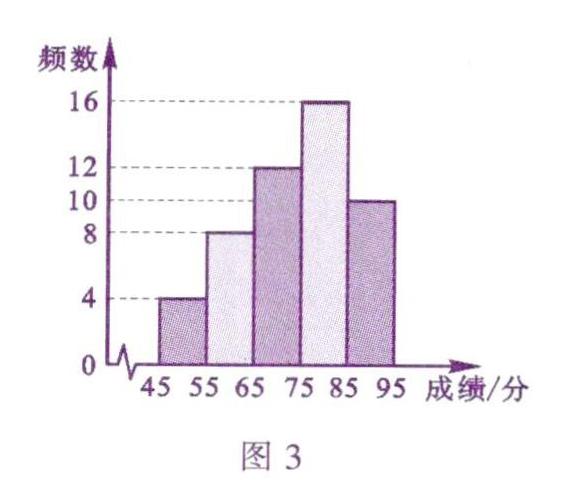
【信息1】A小区50名居民成绩的频数分布直方图如图3（每组含前一个边界值，不含后一个边界值）.

【信息2】上图中，从左往右第四组的成绩（单位：分）如下：

【信息3】A，B两小区各50名居民成绩的平均数、中位数、众数、优秀率（80分及以上为优秀）、方差等数据如下（部分空缺）：

根据以上信息，回答下列问题：

（1）求A小区50名居民成绩的中位数.

（2）请估计A小区500名居民中成绩能超过平均数的人数.

（3）请尽量从多个角度，选择合适的统计量，分析A，B两小区参加测试的居民掌握垃圾分类知识的情况，

解：（1）因为有50名居民，所以中位数落在从左往右第四组，中位数为75分.

（2） 500x24=240（人）.

（3）分三个不同层次进行评价.

甲层次：从一个统计量进行分析.

从平均数看，两个小区居民垃圾分类知识测试成绩的平均水平相同：

从中位数看，B小区至少有一半的居民成绩高于平均数，而A小区则没有;

从众数看，A小区测试成绩的众数高于B小区的众数：

从优秀率看，B小区测试成绩的优秀率高于A小区的优秀率：

从方差看，B小区居民垃圾分类知识的测试成绩比A小区稳定.

乙层次：从两个统计量进行分析.

比如，从平均数看，两个小区居民垃圾分类知识测试成绩的平均水平相同：从方差看，B小区居民垃圾分类知识测试成绩比A小区稳定.因此，B小区居民对垃圾分类知识掌握的情况要比A小区好.

丙层次：从三个及以上统计量进行分析，

从平均数看，两个小区居民垃圾分类知识测试成绩的平均水平相同;从中位数看，B小区的高于A小区的;从优秀率看，B小区的优秀率高于A小区的优秀率，因此，B小区居民对垃圾分类知识掌握的情况要比A小区好，

点评：读懂统计图表，从不同的角度得到全面的信息，是进行多角度评价的关键.根据两个或两个以上统计量进行分析，还可以得到更多的评价.