用一次函数设计方案
张义

一次函数刻画现实世界数量之间的变化关系,不等式则刻画现实世界数量之间的大小关系,它们联袂可以解决现实生活中的方案优化设计、投资费用评估、生产获利计算等问题,有关的试题也备受命题专家青睐,成为中考中一道亮丽的风景线.本文选取数例加以剖析,供大家参考.
例1 某厂现有A种金属70 t.B种金属52 t,计划用这两种金属生产M,N两种型号的合金产品共80 000套,已知生产一套M型号的合金产品需要A种金属0.6 kg,B种金属0.9 kg,可获利润45元;生产一套Ⅳ型号的合金产品需要A种金属1.1 kg,B种金属0.4 kg,可获利润50元,设生产N型号的合金产品x套,用这批金属生产这两种型号的合金产品所获的总利润为y元.
(1)求y与x的函数关系式,并求自变量x的取值范围.
(2)在生产这批合金产品时,Ⅳ型号的合金产品生产多少套时该厂所获利润最大?最大利润是多少?
不等式组的解集是40 000 ≤x≤44 000.
∴ y与x的函数关系式是
y=5x+3 600 000(40 000≤x≤44 000).
(2)因k=5>0,故y隨x的增大而增大.
∴当x=44 000时,有y最大=3 820 000.
即生产N型号的合金产品44000套时,该厂所获利润最大,最大利润是3 820 000元.
评注:利用一次函数解决最大利润问题,一般是根据题目中提供的条件选取一个与利润有关的变量,先列出关于这个变量的一次函数关系式.然后求出这个变量的取值范围(可以结合已知条件列出关于这个变量的不等式组进行确定).虽然一次函数的图象是一条直线,但当自变量限定在某一范围内时,两个端点处的函数值就是其最值.根据一次函数的增减性便可确定最大值或最小值.
例 2康乐公司在A.B两地分别有同型号的机器17台和15台,现要把这些机器运往甲地18台,运往乙地14台.从A,B两地运往甲、乙两地的费用如下:
(1)如果从A地运往甲地x台,求完成以上调运所需总费用y(元)与x(台)的函数关系式.
(2)请你为康乐公司设计一个最佳调运方案,使总的费用最少.最少的费用是多少?
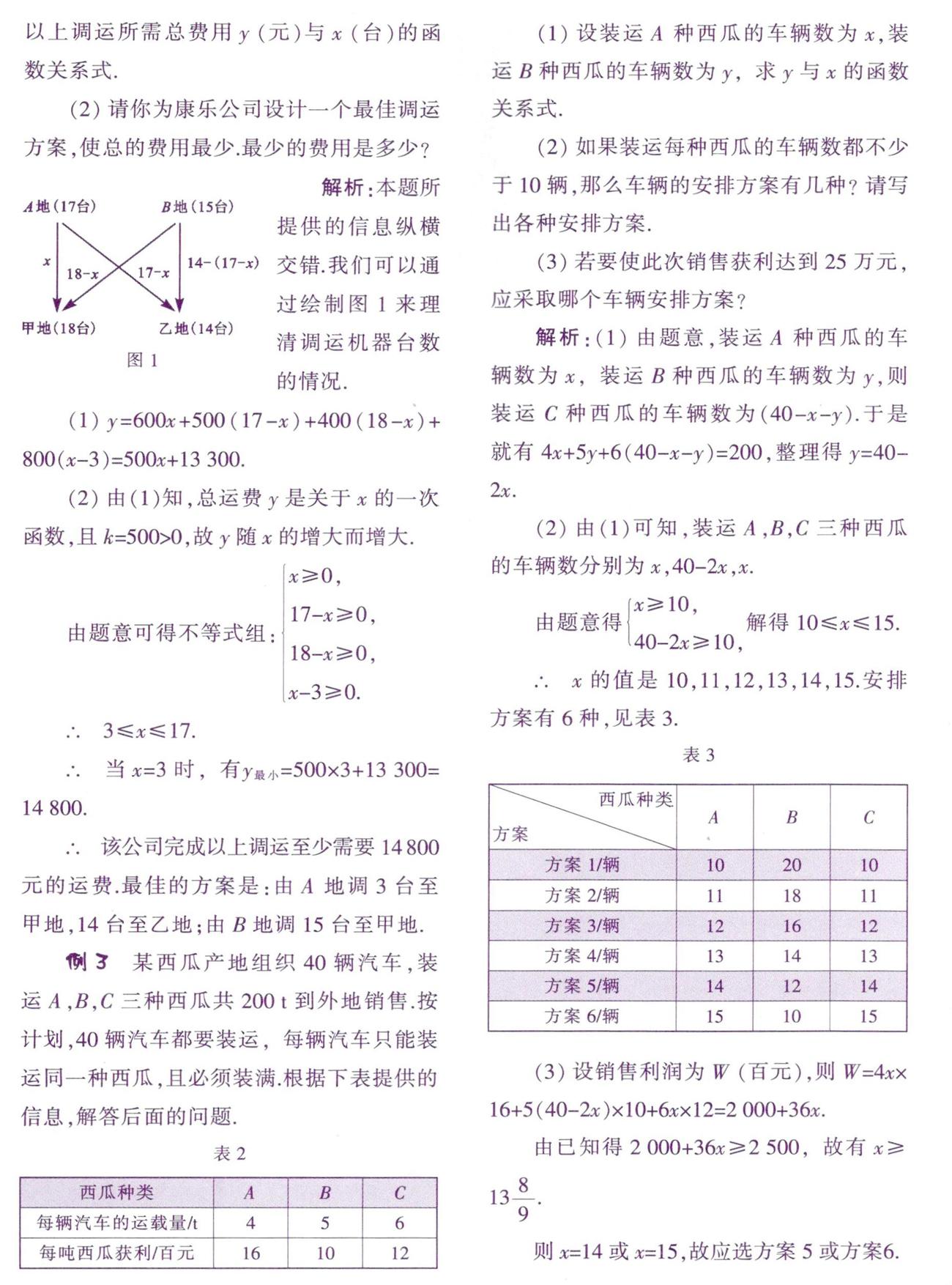
解析:本题所提供的信息纵横交错.我们可以通过绘制图1来理清调运机器台数的情况.
(1) y=600x+500(17 -x)+400(18-x)+800(x-3)=500x+13 300.
(2)由(1)知,总运费y是关于x的一次函数,且k=500>0,故y随x的增大而增大.
∴该公司完成以上调运至少需要14 800元的运费,最佳的方案是:由A地调3台至甲地,14台至乙地:由B地调15台至甲地.
例3 某西瓜产地组织40辆汽车,装运A,B,C三种西瓜共200 t到外地销售,按计划,40辆汽车都要装运,每辆汽车只能装运同一种西瓜,且必须装满.根据下表提供的信息,解答后面的问题.
(1)设装运A种西瓜的车辆数为戈,装运B种西瓜的车辆数为y,求y与x的函数关系式.
(2)如果装运每种西瓜的车辆数都不少于10辆,那么车辆的安排方案有几种?请写出各种安排方案.
(3)若要使此次销售获利达到25万元,应采取哪个车辆安排方案?
解析:(1)由题意,装运A种西瓜的车辆数为x,装运B种西瓜的车辆数为y.则装运C种西瓜的车辆数为(40-x-y).于是就有4x+5y+6 (40-x-y)=200,整理得y=40-2x.
(2)由(1)可知,装运A,B,C三种西瓜的车辆数分别为x,40-2x,x.
由题意得{x≥10. 解得10≤x≤15.
40-2x≥10
∴x的值是10,11,12,13,14,15.安排方案有6种,见表3.
(3)设销售利润为W(百元),则W=4x×16+5 (40-2x)x10+6xx12=2 000+36x.
由已知得2 000+36x≥2 500.故有x≥13 8/ 9
则x=14或x=15,故应选方案5或方案6.
- 中学生数理化·八年级数学人教版的其它文章
- 用数学写就的名言
- 从勾股定理到佘弦定理
- 一道课本习题的变式研究
- “算两次”思想的妙用
- 二次根式如何比较大小
- 勾股定理的常见应用

