大埋深对明挖地铁车站出入口结构影响分析
汪子豪 欧阳院平 洪亮

摘 要:以武汉地铁 12 号线某明挖车站的出入口结构为背景,计算分析出入口结构顶板底埋深 5m、9m 和 18m 3 种条件下不同结构截面时的结构受力,分析大埋深对出入口结构的影响。结果表明,与一般埋深下的出入口结构不同,当结构埋深较大时,结构自重对受力影响相对较小,增加截面尺寸能够显著降低结构受力;在作对比分析时,引入正则弯矩概念,对不同埋深时结构正则弯矩与结构截面的关系进行计算分析,进而对大埋深出入口结构截面进行优化。
关键词:地铁;明挖车站;大埋深;出入口结构;正则弯矩;优化分析
中图分类号:U231.3
地铁明挖地下车站出入口附属结构作为联系外部空间和车站内部空间的主要通道,其安全性十分重要,结构设计还应兼顾其经济性。出入口通常在地下一层与主体结构相连接,其基坑开挖深度一般在10 m左右,工程计算中,往往可以采用较为固定的断面设计尺寸[1-4]。然而随着地铁建设规模逐步扩张,线网规划趋于复杂,附属结构的设计受限于建筑红线、控制管线、交通组织、线路换乘等因素[5-8],大埋深出入口的非典型情况越来越多见[9-10]。
本文结合武汉地铁12号线某出入口结构实例,研究地下车站出入口结构不同埋深时的结构受力,对大埋深出入口结构截面进行优化。
1 结构设计模型
武汉地铁12号线某明挖车站受限于市政管线改迁和线路交叉等因素,出入口基坑开挖深度最大达20余米。本文采用有限元模拟顶板底埋深5 m~18 m的出入口标准断面。
1.1 基本假定
明挖车站的出入口结构标准断面为箱形钢混结构,结构纵向荷载分布无突变,底板地基承载力均匀,其结构受力分析可简化为平面问题[11-14]。地铁车站结构一般采用弹性分析方法,验算承载力大小和裂缝宽度。计算模型中,底板下设置竖向受压土弹簧支撑;考虑结构最不利受力情况进行荷载组合,迎土面按照0.2mm裂缝控制配筋,背土面和车站内其他部位按照0.3mm裂缝控制配筋[15-17];结构设计按使用年限100年考虑,不考虑抗震工况和偶然组合。
1.2 计算模型
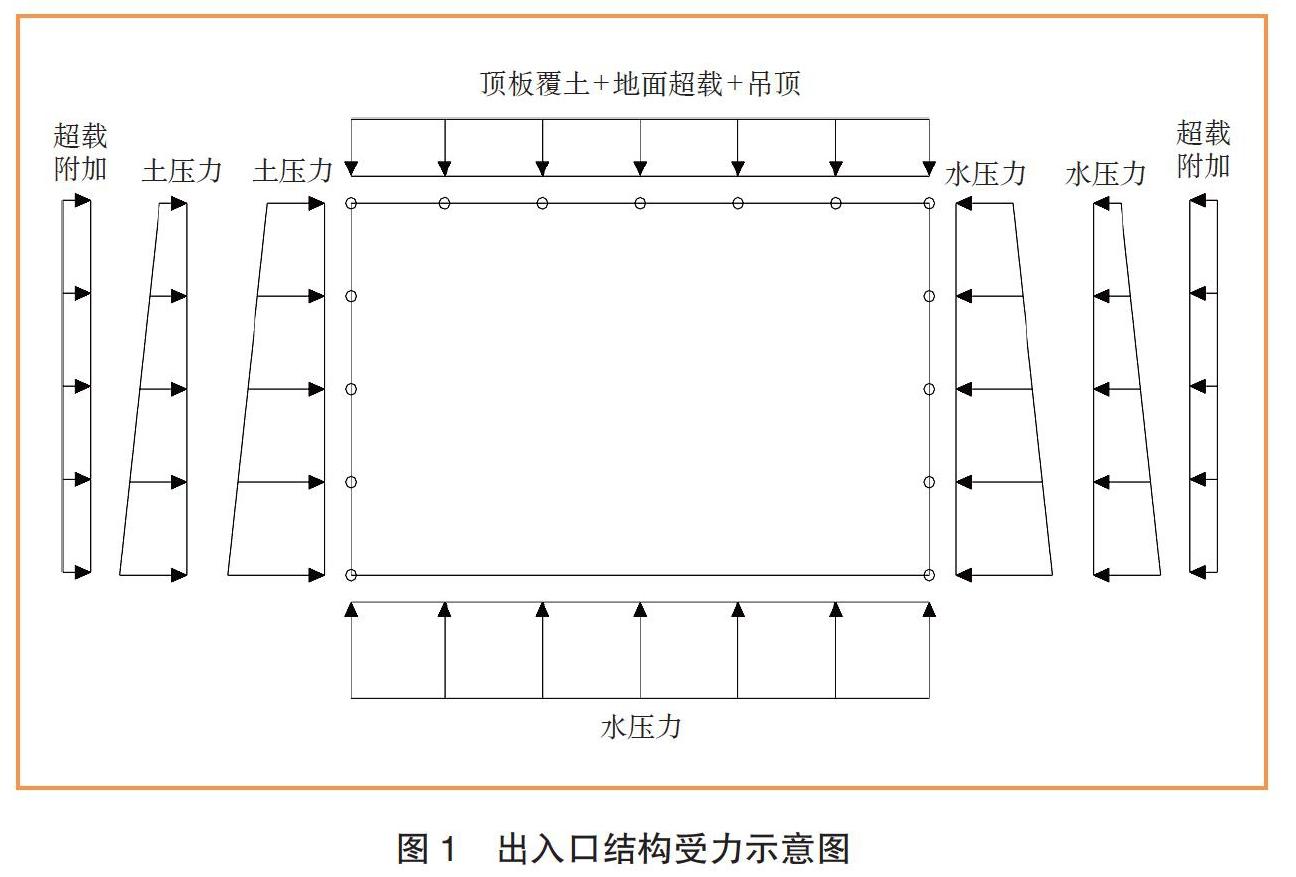
出入口结构标准断面的结构净高4.2 m,净宽6.5m,采用C35抗渗混凝土。计算中,分别对顶板底埋深5m、9 m和18 m3种条件下的出入口结构标准断面进行分析;考虑土压力、水压力、顶板覆土和地面超载4 类荷载作用,偏安全考虑取地表为抗浮水位[18-20],其受力示意图如图1所示。当顶板底埋深为5 m时,出入口底板所受水浮力约为100 kN;当顶板底埋深达到18m时,出入口底板所受水浮力增加约230 kN,相应地,顶板覆土压力也由约40 kN增加至约170 kN。
2 结构模拟分析
本节将对顶板底埋深分别为5 m、9 m和18 m的标准出入口结构进行比较分析,出入口结构断面均为标准断面。结合结构受力和实际情况,对每一种顶板底埋深的情况取5~7组结构尺寸组合,如表1所示。
分别计算不同结构厚度下的结构内力,综合比选承载力和裂缝分析结果,得到不同埋深条件下的最优结构尺寸。当荷载条件相同时,随着结构尺寸变化,结构内力也会发生变化;结构厚度越大的截面,其承载能力越强。为便于对比,本节将采用板厚对弯矩进行正则化。
2.1 顶板底埋深 h = 5 m 出入口结构分析
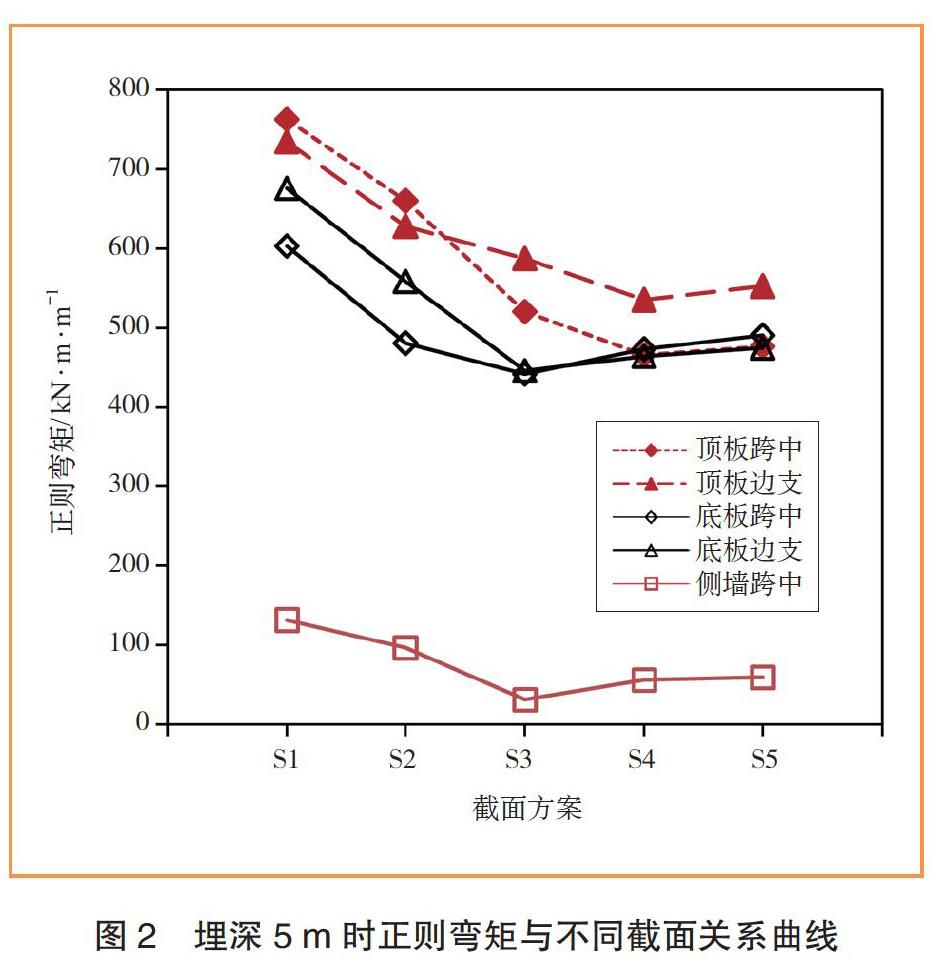
出入口结构顶板底埋深h = 5 m时,不同标准断面尺寸下的准永久弯矩如图2所示,图2中横坐标对应表1中的不同截面方案,纵坐标的正则弯矩为结构弯矩与对应位置截面厚度的比值。
由圖2可知,随着截面厚度的增加,不同截面位置的正则弯矩均呈现出减小趋势;侧墙跨中正则弯矩值相对较小,不是计算结构尺寸的决定性因素;当截面增大到截面方案S3时,底板跨中和边支的正则弯矩均达到最小值;截面方案从S3增加到S4时,顶板、底板及侧墙的厚度均增加100 mm,此时顶板的正则弯矩减小,底板和侧墙跨中则不降反升。由此可见,截面方案S3至S4的截面尺寸增大带来的承载能力提升不显著,不足以抵消底板和侧墙的弯矩增加;此后随着截面增大,正则弯矩几乎不变。
综合考虑结构安全性和经济性,计算顶板底埋深h = 5 m时截面方案S1至S5的承载力和裂缝,此出入口标准截面的最佳截面方案为S3。
2.2 顶板底埋深 h = 9 m 出入口结构分析
出入口结构顶板底埋深h = 9 m时,不同标准断面尺寸下的正则弯矩如图3所示。类似地,随着截面厚度的增加,不同截面位置的正则弯矩均成减小趋势,侧墙跨中弯矩值相对较小;截面方案从S2增加到S3时,仅顶板厚度增加100 mm,此时顶板和侧墙跨中正则弯矩减小,底板则在边支位置正则弯矩减小,在跨中位置相应增加;对于截面方案S3至S5,结构正则弯矩变化幅度较小,即此时截面尺寸增加对结构承载能力的提升效果不显著。
综合考虑结构安全性和经济性,计算顶板底埋深h = 9 m时截面方案S1至S5的承载力和裂缝,此出入口标准截面的最佳截面方案为S3。
2.3 顶板底埋深 h = 18 m 出入口结构分析
出入口结构顶板底埋深h = 18 m时,不同标准断面尺寸下的正则弯矩如图4所示。随着截面厚度的增加,不同截面位置正则弯矩基本保持减小趋势,侧墙跨中正则弯矩值相对较小;截面方案从S2增大到S3时,顶板和底板厚度均增加100 mm,正则弯矩均有明显明显减小;截面方案从S3增大到S4时,仅顶板厚度增加100 mm,此时顶板和侧墙跨中正则弯矩均减小,底板则几乎不变,仅其边支位置正则弯矩略有增加,顶板和底板正则弯矩仍较大,对结构承载力和裂缝进行计算可知,此时结构配筋率仍较高;当出入口结构截面继续增大,即截面方案从S4增大到S5时,仅底板厚度增加100 mm,此时底板正则弯矩显著减小,顶板则变化较小;当截面从S6增大至S7时,仅侧墙厚度增加100 mm,顶板和底板跨中弯矩均略为减小,且各边支处正则弯矩不降反升。由此可见,为优化出入口结构截面尺寸和配筋率,增加底板厚度的效果与增加顶板厚度相一致。

