载重38 800 t散货船推进轴系轴承布置设计
严宏宇
(哈尔滨工程大学, 黑龙江 哈尔滨 150001)
0 引 言
随着远洋航运的不断发展,为提高船舶运输效率,船舶载重吨位也在不断增加,载重吨位不断攀升的同时对船舶传动主轴的要求也愈来愈高。在船舶传动轴的设计中,轴承布置会直接影响船舶推进系统的可靠性。
当船舶采用尾机型推进轴系时,其尾管轴承的布置方案分为两种:一种为仅装备后尾管轴承的单尾管轴承布置方案;另一种为双尾管轴承的方案[1]。
在过去,船舶的轴承布置方案往往使用双尾管轴承的布置方案。在船舶建造日益大型化的发展趋势下,船舶轴系所承载的扭矩也日益增加,船舶轴系在向着轴向缩短、径向增大的方向发展,当船体承受较小的变形时就会引起较大的轴承反力[2]。船体的尺寸增长会导致其刚度减小,在不同载重情况下,船体形变的差距较大,在此基础上,船体同轴系之间的配合情况也变得更加复杂。在此前提下, 关于轴承布置位置的研究就愈发重要。
在船舶轴系轴承布置中,传统布置法往往需要在尾轴部分布置尾管前轴承和尾管后轴承来保证尾轴的可靠性和密闭性。这种布置方法对于长轴系船舶来说是必需的,但是随着制造工艺和材料强度的不断提高,对于短轴系船舶的轴承布置,尾管前轴承的作用变得越来越弱。分别就两种尾管轴承布置方案进行轴承布置优化,以获得最优结果[3]。
1 轴系优化设计方法
1.1 船舶轴承间距设计
选取大型远洋货船,轴系长约13 000 mm,中间轴的长度和中间轴承的布置将直接对船舶轴系的稳定性和可靠性产生影响。轴承间距和数量直接影响轴的应力情况和轴的弯曲变形,适当增长轴承间距能够减少轴承数量、增强轴系柔性,使轴系工作更可靠,尽可能减小变形对轴的影响,甚至能够减小额外的负荷。
轴承跨距可根据轴承间距经验公式求得
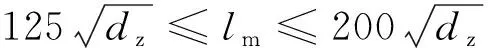
(1)
式中:lm为最大轴承允许跨距,mm;dz为中间轴轴径,mm。
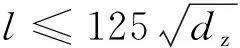

在通常情况下,中间轴长约(0.7~0.8)dz,设最大许用比压p≤0.59 MPa,因此可推出:
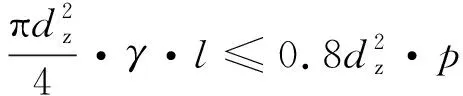
(2)
式中:取γ=76.9 N/mm3。
在船舶航行过程中,往往会存在由船体变形和轴系加工安装误差导致的附加载荷,当轴承间距过小时,附加载荷会过大,因此,对于轴承的间距,不仅应该考虑其最大间距,而且其最小间距也应该列入其考虑范围:

(3)
在最终进行轴系的整体设计时,应该保证轴承间距l>lmin,但同时也不能使轴承间距过大。一方面,若间距过大会导致轴系整体在回转运动时产生较强的回转振动和横向振动;另一方面,轴承间距过大会导致相应中间轴长度过长,导致整体轴线的挠度增加,并且同时也为中间轴的安装和加工带来诸多麻烦。
1.2 轴系优化设计理论
基于数值方法对船舶轴系优化研究主要有两种形式:其一为通过改变轴系中零部件参数,并对不同参数情况下的轴系分析结果进行比较来选取最优解;其二为在数值计算的基础上,改变轴系中的各种参数,并寻找各参数与结果之间的关系,通过拟合近似等多种算法得到整个系统中各参数的最优解。在有限元分析的基础上采用响应面法优化整个船舶推进轴系点的多个参数,整个优化流程如图 1所示。

图1 优化分析流程
对于优化设计,需要其数学模型满足规范化的要求,即需要把对于整个轴系的优化设计问题通过数学方式进行描述[4]。在一般情况下,优化设计可归纳为:首先确定约束范围,然后在优化范围内选取一些设计变量作为优化指标,最后分别确定各设计变量使目标函数达到最大值或最小值。其数学表达式为
min{f(x)1,f(x)2,…,f(x)n};x∈X⊂Rn
(4)
gu(x)≤0;u=1,2,…,m
(5)
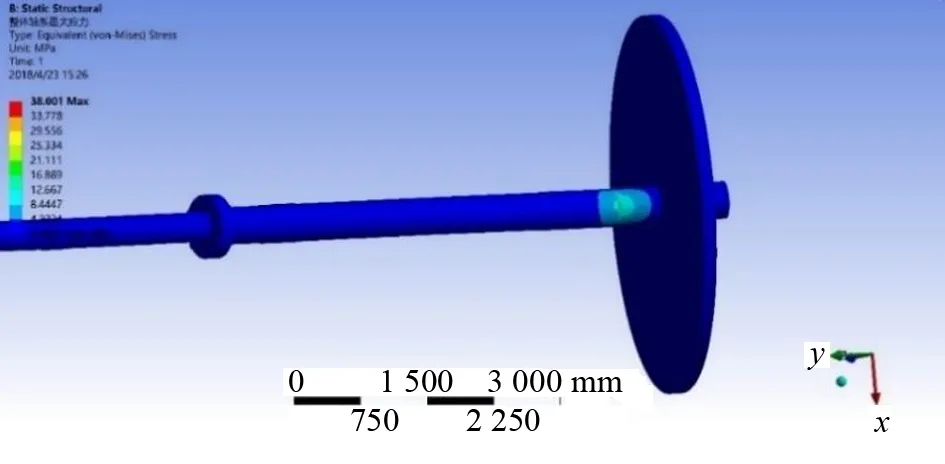
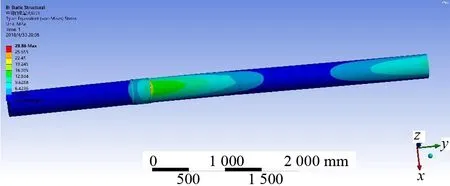
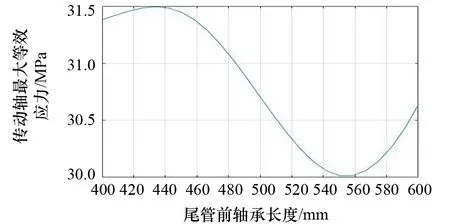
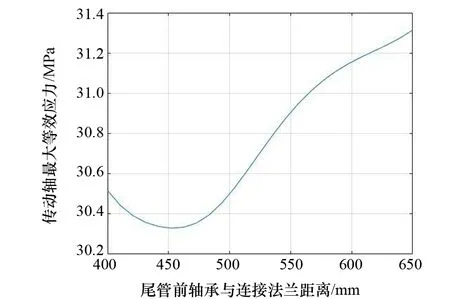
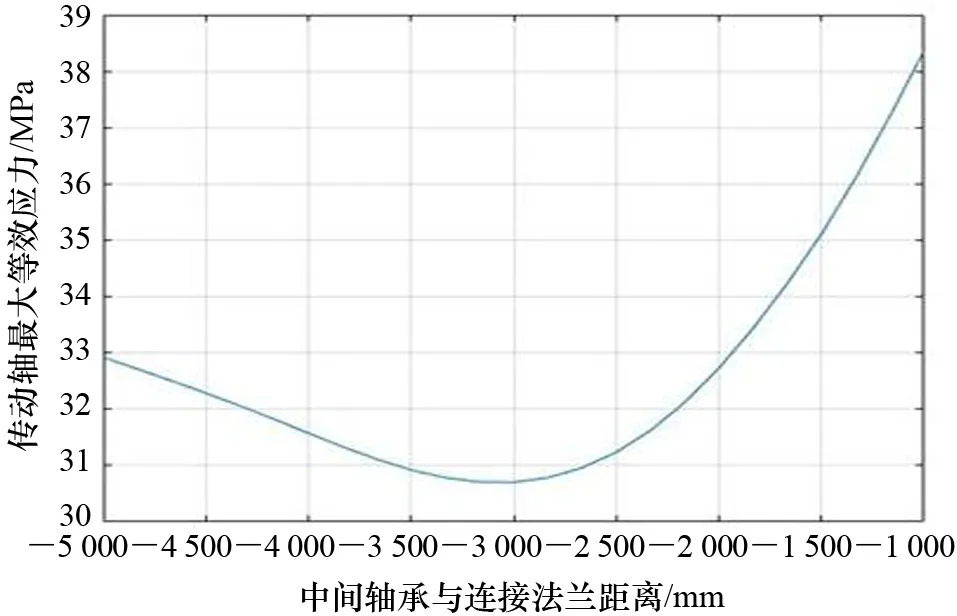
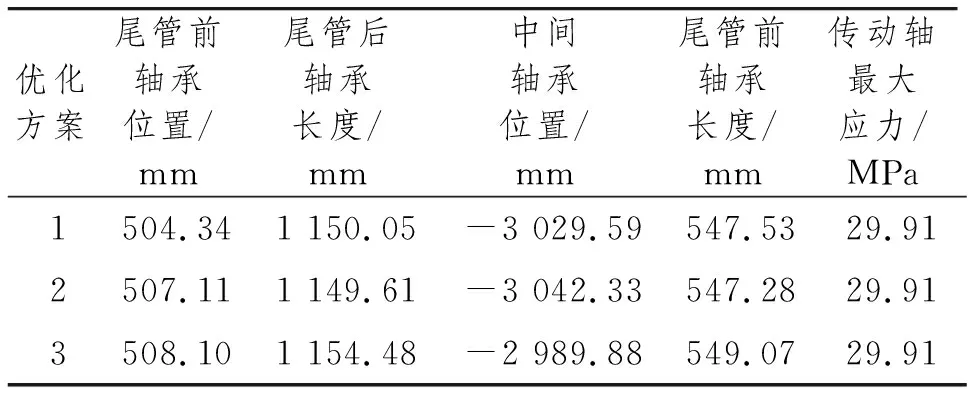
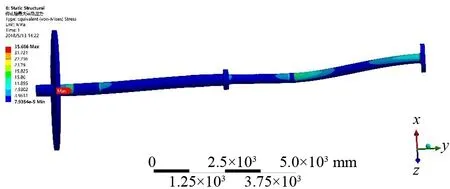
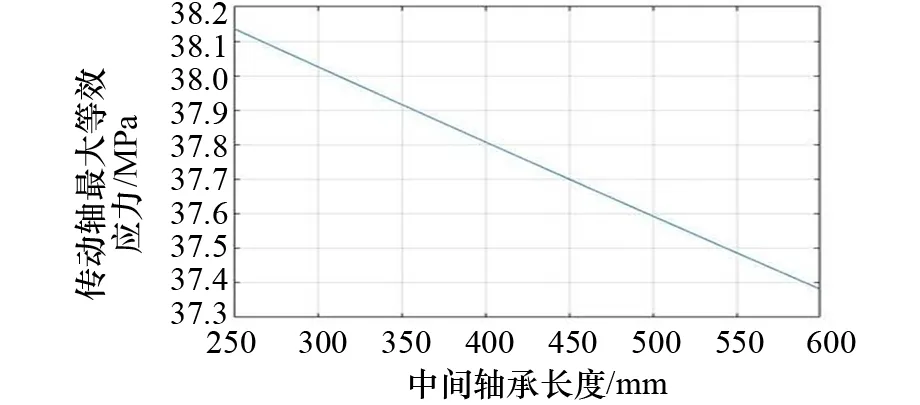
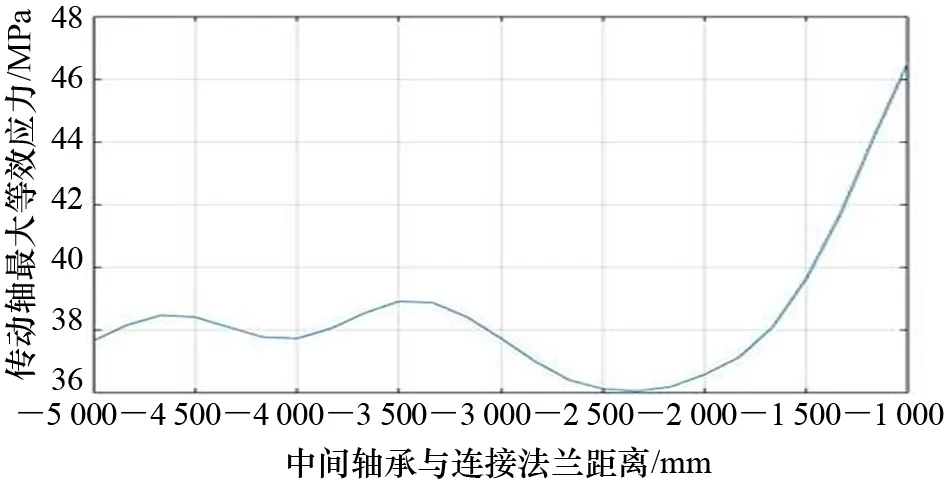
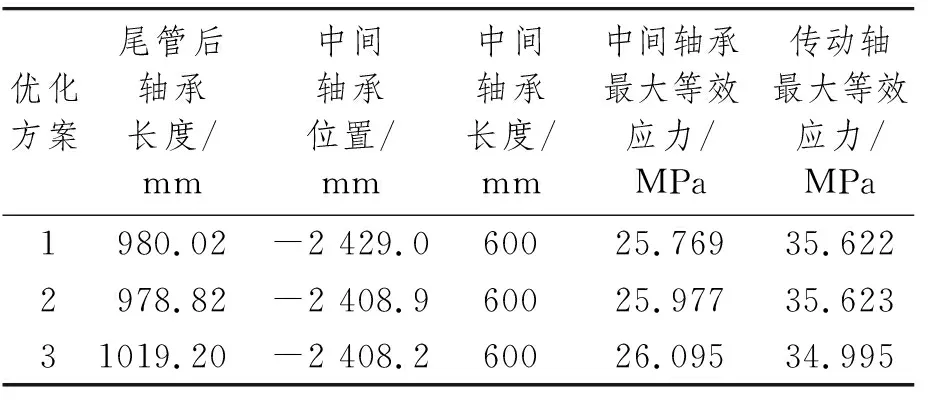
hv(x)=0;v=1,2,…,p (6) 即x=[x1,x2,x3,…,xn]T。式(4)~式(6)中:gu(x)为第一约束条件;hv(x)为第二约束条件;X为符合一定条件的设计变量向量的合集;Rn为n维欧氏空间。 载重38 800 t散货船轴系整体长度为13 000 mm,根据轴承间距设计理论,确定整个推进轴系的轴承布置位置,尾管后轴承在距离连接法兰3 600 mm处,尾管前轴承在距离连接法兰600 mm处,中间轴承在距离连接法兰1 500 mm处,轴肩设计为15 mm。根据设计参数在UG11.0中建立轴系的三维模型,并更改上述各参数名为英文前缀DS_,以便导入ANSYS Workbench中能够被识别。可以发现:在选定设计参数时,既选定轴承长度,又选定轴承距法兰位置,此时如果2个设计参数相互独立,则会产生冲突。为避免冲突,应对各设计参数确定相互之间的关系[5]。 从整体推进轴系来看,尾管后轴承的长度、尾管前轴承前端距法兰距离、尾管前轴承后端距法兰距离、中间轴承前端距离法兰位置、中间轴承后端距离法兰位置等共同决定整体轴系的基础结构,选取上述参数为宏观优化参数[6]。 分析中主要考虑轴系在稳态过程中的载荷情况对整体轴系的影响,仍选择Workbench中的静力学模块。通过UG11.0和ANSYS Workbench的软件接口模型导入模型,在3个轴承位置分别设置圆柱形约束,只约束其径向位移,对轴系进行第一次分析,为了直观地显示轴承附近的等效应力,在后处理时,展示部分轴段的应力分析结果。 重点分析轴承布置间距对船舶轴系的影响,螺旋桨采用等转动惯量、等重量圆盘替代,三维模型如图2所示。 图2 轴系螺旋桨模型 在参数优化过程中,先进行参数敏感性研究,调用Workbench中内置的parameters correlation模块进行整体参数相关性分析。该模块通过更改设置的优化参数,调用静力学分析的结果,研究各参数之间的相关关系,整个系统模型如图3所示。图3中,A模块为由UG11.0导入的参数化后的轴系几何模型,B模块为静载荷计算模块,C模块为参数相关性模块,D模块为响应面参数优化模块。在这个系统模型中,C模块设计试验点,并通过设计试验点更改所选定的优化参数的值,再利用该值进行有限元静力学分析,得到设定的优化结果(即推进轴系各项应力),从而得到各参数之间的相关性。 图3 宏观参数优化系统模型 在双尾管轴承船舶轴系分析中,主要考虑轴系在冷态过程中的载荷情况对整体轴系的影响,仍选择Workbench中的静力学模块。通过UG11.0和Workbench 的软件接口模型导入模型。 在3个轴承位置分别设置圆柱形约束,对整个轴系施加重力载荷。分析结果如图 4所示。 图4 推进轴系最大等效应力 宏观层面的优化旨在通过改变尾管前轴承位置和中间轴承位置使轴系在这两部分的载荷分布更均匀。因此,在后处理过程中,尾管前轴承附近最大等效应力和中间轴承附近最大等效应力分别如图 5和图 6所示。 图5 尾管前轴承附近最大等效应力 图6 中间轴承附近最大等效应力 根据有限元分析,中间轴最大等效应力为28.860 MPa,尾管前轴承部分最大等效应力为2.360 MPa,而整体轴系的应力主要集中于尾管后轴承部分,其承载的应力为38.001 MPa。由力学分析可知,改变尾管前轴承和中间轴承位置,可适当减小尾管后轴承的应力情况,由于轴系最大等效应力过大会造成轴系断裂或轴系变形,因此选择整个轴系最大等效应力为优化目标。 根据试验点进行参数敏感性分析,分析结果如图 7所示,可发现:对整体传动轴应力敏感性最强的是中间轴承位置和尾管后轴承长度,而尾管前轴承的位置对最大轴系应力敏感性最弱;在中间轴承最大应力敏感性柱状图中,中间轴承的位置敏感性较强,其余3项敏感性较弱;在尾管后轴承压力敏感性柱状图中,中间轴承的位置敏感性最强。尾管后轴承长度与传动轴最大等效应力关系如图 8所示,可发现:尾管后轴承的长度在1 000~1 100 mm 时,传动轴的最大等效应力最小,因此在设计过程中应使尾管后轴承长度位于这个区间。 图7 双尾管轴承参数敏感性 图8 尾管后轴承长度和传动轴最大等效应力关系 尾管前轴承长度与传动轴最大等效应力关系如图 9所示,可发现:尾管前轴承长度在540~560 mm时,整个传动轴的最大等效应力较小。尾管前轴承位置与传动轴最大等效应力关系如图 10所示,可发现:尾管前轴承距连接法兰450 mm处时整个传动轴承的等效应力最小,尾管前轴承过于靠近法兰则会增大整个传动轴的最大等效应力。尾管前轴承在轴系布置中承受的应力较小,改变其长度和位置对整体传动轴最大等效应力的影响也较小,在后续优化过程中可调节轴承的长度以加强其支承作用。 图9 尾管前轴承长度与传动轴最大等效应力关系 图10 尾管前轴承位置和传动轴最大等效应力关系 中间轴承位置与传动轴最大等效应力关系如图 11所示,可发现:当中间轴承位于-3 100 mm(以连接法兰为原点向螺旋桨端为正,向主机端为负)的位置时,传动轴最大等效应力最小,并且中间轴承对传动轴的最大等效应力影响较为显著,中间轴承位置应为主要优化参数之一。 图11 中间轴承位置和传动轴最大等效应力关系 在完成推进轴系的参数敏感性计算后,试验点采用MOGA法进行数据拟合,并通过拟合模型得到了最优的3个推荐方案,如表 1所示。这3个方案整体轴系最大应力降低约8 MPa,各方案之间大致相同。由于船舶航行时螺旋桨会产生较大推力扭矩,最终优化结果应同时考虑热态情况。 表1 双尾管轴承参数优化方案 根据第2节对于有尾管前轴承的传动轴最大应力分析可以发现,尾管前轴承附近载荷较小,尾管前轴承的位置和长度的改变对整个推进轴系最大应力的影响也较小。在进行轴承布置时,考虑不设置尾管前轴承,并采用特殊定制中间轴承以增加中间轴承的长度[7]。主要研究不布置尾管前轴承情况下整个轴系的最大等效应力优化。 通过UG11.0导入ANSYS Workbench,并设置中间轴承位置、尾管前轴承位置、尾管前轴承长度和尾管后轴承长度等4个参数作为优化参数。选用Workbench中的静力学分析模块进行分析,尾管后轴承和中间轴承位置分别设置圆柱形约束,对整个轴系施加重力载荷。 分析结果如图12所示,可发现:传动轴系的最大等效应力为35.686 MPa,最大应力点位于尾管后轴承靠近螺旋桨端,主要由螺旋桨重力导致。 图12 无尾管前轴承推进轴系等效应力 在载荷下,未优化轴承布置位置前,中间轴承最大等效应力为34.459 MPa,如图 13所示,主要集中在中间轴承靠近推力轴部分。选择中间轴位置和长度及尾管后轴承的长度为优化参数,选择传动轴的最大应力为优化指标进行优化。 图13 参数优化前中间轴承最大等效应力 在参数优化设置中,使用最优空间填充设计中的最大熵设计类型进行参数设计,共选取50组参数进行分析,其参数敏感性如图 14所示,可发现:在中间轴承的最大等效应力中,中间轴承位置的敏感性最高,改变中间轴承位置对中间轴承最大等效应力的影响最为显著。从传动轴最大应力敏感性柱状图中能够看出,中间轴承位置最高,敏感性分析结果也符合有限元分析模型,整体轴系的最大等效应力往往集中于中间轴承和尾管后轴承处。 图14 无尾管前轴承轴系参数敏感性 轴承布置的最终目标是使船舶轴承的布置能够保证每个轴承受力均等,且整个轴系的最大应力最小,因此,整体轴系的最大等效应力就成为了最重要的优化指标,同时各设计优化参数与优化指标之间的关系就显得格外重要。 尾管后轴承长度与传动轴最大等效应力关系如图 15所示,可发现:尾管后轴承的长度越长传动轴的最大等效应力值越大,因此在设计过程中应当避免尾管后轴承长度过长。同时,尾管后轴承过长也存在浪费材料和减小轴系的柔性等问题,因此尾管后轴承长度大概取值为800~1 100 mm。 图15 尾管后轴承长度与传动轴最大等效应力关系 中间轴承位置与传动轴最大等效应力关系如图 16 和图 17所示,可发现:当中间轴承位于-2 400 mm 左右时,传动轴最大等效应力最小,并且中间轴承对传动轴的最大等效应力影响较为显著,中间轴承位置应为最主要优化参数。 图16 中间轴承长度与传动轴最大等效应力关系 图17 中间轴承位置和传动轴最大等效应力关系 对轴承布置进行优化求解,为保证所有轴承附近的轴段等效应力均匀,约束中间轴承附近的应力范围取值为35~45 MPa,约束尾管前轴承附近的应力范围取值为35~45 MPa,设置推进轴最大应力优化目标为最小值。参数设计的最终优化方案如表 2所示,3个优化方案基本一致,与设置有尾管前轴承的整个推进轴系的布置方案相比,不设置推进轴系的方案需要前移中间轴承,中间轴承位于距离连接法兰2 400 mm处最佳,且应当适当地增大中间轴承长度,以保证中间轴承的可靠性。 表2 单尾管轴承参数优化方案 (1) 将有限元模拟的方法和优化设计法结合,分别就单尾管轴承和双尾管轴承两种轴承布置型式进行研究,发现在使用单尾管轴承布置方案时,轴系受力略大于使用双尾管轴承布置方案。 (2) 对轴承布置参数进行敏感性分析,当采用双尾管轴承和单尾管轴承时,中间轴承位置敏感性最高。 (3) 与双尾管轴承布置方案相比,单尾管轴承布置方案的最佳设计应前移中间轴承。针对轴承位置和轴承长度等多个因素对轴系受力状况的共同影响进行分析,对大型运输船轴系布置有一定的意义和参考价值。1.3 轴承布置优化设计流程


2 双尾管轴承布置方案优化



3 单尾管轴承布置方案优化



4 结 论

