舱内爆炸载荷作用下舱壁板的动力响应分析

李虹熹， 李晓彬

(武汉理工大学 交通学院， 湖北 武汉 430063)

0 引 言

在现代海战中，舰船是主要的受攻击对象，是海军部队赖以生存和发动攻击的平台。导弹穿透舰船的舷侧外板，在舱室内部爆炸，会产生大量的高速破片，对舱壁结构产生侵彻作用[1]，甚至毁伤舰船内部设施和人员，对舰船造成致命打击。因此，研究舰船舱壁结构的动态响应和防护性能，对提高舰船的抗爆能力和安全性具有重大的现实意义和军用价值[2]。由于舱室的每个舱壁通常与该舱室的其他舱壁及相邻舱室的舱壁相连接，为快速得到某个舱室舱壁在舱内爆炸载荷作用下的动力响应，可以将该舱壁从舱室结构中隔离出来，其他结构对该舱壁的影响可简化为边界条件来描述。舱壁的边界条件对舱壁的动力响应有较为显著的影响，国内外众多学者[3-7]研究不同边界条件下矩形平板或板架的振动、变形和断裂。吴成等[8]对固支方板在爆炸冲击作用下变形的最终挠度进行理论推导及试验研究，结果表明边界的约束条件对靶板的变形有很大的影响。在研究舱内爆炸载荷作用下舱壁板动力响应的过程中，上述学者均采用流固耦合的方法，但这种方法需要消耗大量的计算资源和时间，推荐采用解耦的方法更具优势。用解耦的方法首先可得到舱内爆炸时作用于舱室各舱壁上的压力时间历程，再将该压力载荷作用到舱室各舱壁上得到其动力响应。采用有限元软件Abaqus建立完整的舱室结构模型和几种具有不同边界条件的舱壁板模型，分别用于研究舱内爆炸载荷作用下舱壁板的动力响应，并比较各种模型的计算结果。

1 舱室结构模型简介

1.1 Abaqus算法

Abaqus算法采用直接积分法中的显式中心差分法。显式中心差分法适用于研究波的传播问题，比如碰撞、高速冲击、爆炸等。采用显式中心差分法时质量矩阵M与阻尼矩阵C是对角阵，如给定某些有限元节点以初始扰动，在经过一个时间步长后，与这些节点相关的一些节点开始运动，即位移向量U中这些节点对应的分量成为非零量，此特点正好与波的传播特点相一致。另一方面，由于波传播的过程非常迅速，因此研究该过程需要采用很小的时间步长，这也正是显示中心差分法的特点。

1.2 材料特性

舱室结构的材料为45钢，采用Johnson-Cook本构模型，即J-C模型，其动态屈服强度为

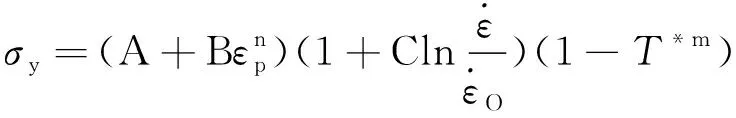
(1)

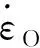
1.3 载荷设置

英国劳氏船级社(LR)规范[10]对舱内爆炸主要考核准静态超压对舱壁的破坏效应，其目的在于限制爆炸损伤扩展到邻近舱室，该规范提到：冲击波和准静态超压都会使结构失效。若武器具有足够的当量通过冲击波造成损伤，冲击波也会在基于准静态超压的阶梯函数评估中损伤。因此，对于一般设计，可以采用基于准静态超压的阶梯函数作为失效载荷的判据。

根据文献[10]，准静态压力计算如下：

(2)

式中：Pqs为准静态压力，kN/m2；We为等效TNT当量，kg，根据试验取400 kg；V为舱室体积，m3。

1.4 结构模型及计算结果

对于大部分船型而言，每个舱室并非孤立地存在于船体内，而是与周围舱室相互连接在一起。研究的舱壁板位于舯部附近，如图1所示。

图1 实际船舶舱室及有限元模型

为便于后续研究，将完整的舱室结构等效成18个完全相同的舱室，每个舱室的几何尺寸均为3.0 m×2.5 m×2.5 m，去除加强构件，通过等重量原则增加板厚至16 mm，有限元网格是边长为0.1 m 的四边形网格。边界条件设置为整个舱室结构的边缘刚性固定，施加边界约束，通过式(2)计算得到均匀分布的准静态压力为20.375 3 MPa，加载位置为沿舱室纵向的正中间舱壁，完整的舱室结构模型如图2所示。

由于舱内爆炸过程非常迅速，计算时间通常采用毫秒级别，取50 ms，在隐藏外侧舱壁结构后，周边板的变形很小，可忽略不计，加载舱壁在最终时刻的变形云图如图3所示，最大变形为374.9 mm。

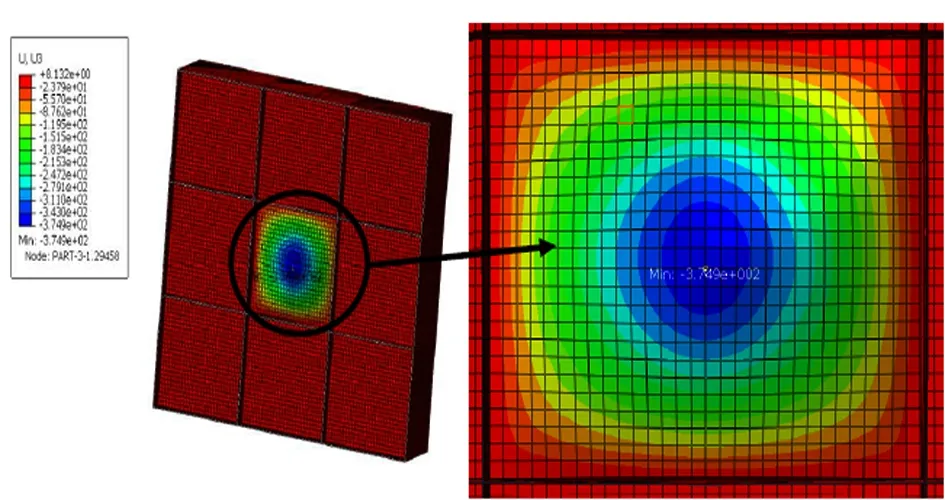
图3 完整的舱室结构模型中舱壁的最终变形云图

2 舱壁模型

将舱壁从舱室结构中隔离出来，用于计算舱内爆炸载荷作用下舱壁板的动力响应。舱壁板模型的几何尺寸为3.0 m×2.5 m，板厚为16 mm，有限元网格为100 mm×100 mm的四边形网格，材料参数及载荷与第1.2节相同，舱壁板法向为z轴。每个节点有6个自由度，包括：沿3条坐标轴方向的位移自由度，分别为U1、U2、U3；绕3条坐标轴的转角自由度，分别为UR1、UR2、UR3。

2.1 全约束

很多学者研究爆炸载荷作用下四边固支舱壁板的动力响应和损伤模式，例如侯海量等[11]通过有限元分析程序研究爆炸载荷作用下4边固支矩形加筋板的失效模式。假定舱壁板的4边刚性固定(即6个自由度被全部约束)，研究舱内爆炸载荷作用下舱壁板的动力响应，计算时间取50 ms，所得到的结果如图4和图5所示，最终时刻舱壁板中心的位移为354.3 mm。

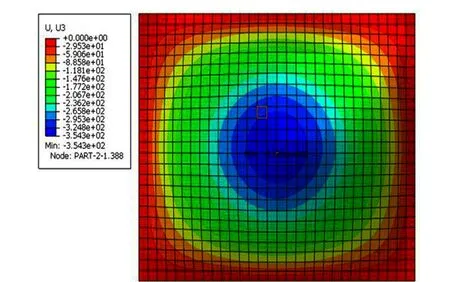
图4 4边刚性固定舱壁板的最终变形云图

图5 分别释放U1、U2、U3的约束后舱壁板的变形分布

通过对比图4和图3可以发现：对舱壁板四周进行全约束所得到的舱壁板中心位移比从整体舱室结构模型所得到的舱壁板中心位移小。这表明：舱壁板四周的约束条件过强，有必要进一步研究舱壁板四周的边界条件。

2.2 释放位移自由度约束

分别释放舱壁板4边的位移自由度U1、U2和U3的约束，保留3个转角自由度约束，研究舱内爆炸载荷作用下舱壁板的动力响应。计算时间仍取50 ms，最终时刻舱壁板的面外位移沿舱壁板长度方向，即通过舱壁板两短边中点的分布如图5所示。分别释放U1、U2和U3的约束后所得到的最终时刻舱壁板中心位移分别为478.8 mm、577.4 mm和27 020.0 mm。

如图5所示：释放U1或U2的约束后舱壁板中心位移变大且超过了从完整舱室结构模型所得到的舱壁板中心位移。这表明：释放U1或U2约束对舱壁板中心位移有很大的影响；释放U3的约束后整个舱壁板作刚体运动，此处不予考虑。因此，不应当释放任何一个沿坐标轴方向的位移自由度约束。

2.3 释放转角自由度约束

(1) 分别释放舱壁板4边的转角自由度UR1、UR2、UR3的约束，保留3个位移自由度约束，研究舱内爆炸载荷作用下舱壁板的动力响应。计算时间取50 ms，最终时刻舱壁板的面外位移沿舱壁板长度方向，即通过舱壁板两短边中点的分布如图6所示。分别释放UR1、UR2和UR3的约束后所得到的最终时刻舱壁板中心位移分别为354.4 mm、354.1 mm 和354.3 mm。

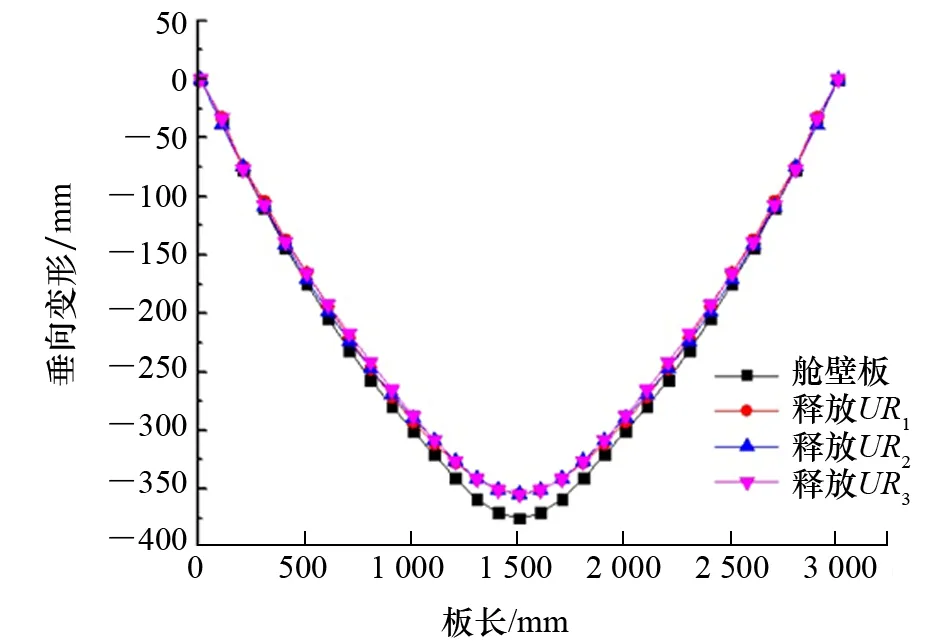
图6 分别释放UR1、UR2、UR3的约束后舱壁板的变形分布

如图6所示：释放UR1或UR2的约束后舱壁板中心位移只有微小的变化且比从完整舱室结构模型所得到的舱壁板中心位移小。这表明：释放UR1或UR2的约束对舱壁板中心位移只有微小的影响；释放UR3的约束后舱壁板中心位移几乎没有变化，这说明释放UR3的约束对舱壁板中心位移没有影响。

(2) 分别释放舱壁板4边的2个转角自由度UR1和UR2、UR1和UR3及UR2和UR3的约束，保留3个位移自由度约束，研究舱内爆炸载荷作用下舱壁板的动力响应。计算时间取50 ms，最终时刻舱壁板的面外位移沿舱壁板长度方向，即通过舱壁板两短边中点的分布如图7所示。分别释放UR1和UR2、UR1和UR3及UR2和UR3的约束后所得到的最终时刻舱壁板中心位移分别为358.7 mm、354.4 mm 和354.1 mm。

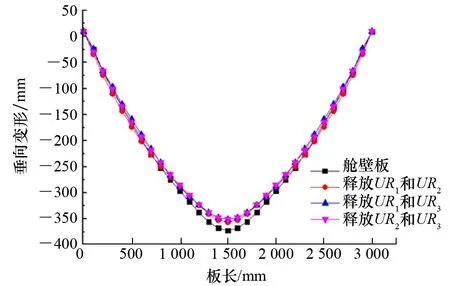
图7 分别释放舱壁板4边的2个转角自由度约束后舱壁板的变形分布

如图7所示：释放UR1和UR2或UR2和UR3的约束后舱壁板中心位移只有微小的变化，并且比从完整舱室结构模型所得到的舱壁板中心位移小，因此释放UR1和UR2或UR2和UR3的约束对舱壁板中心位移只有微小的影响；释放UR1和UR3的约束后舱壁板中心位移略有增加且与从完整舱室结构模型所得到的舱壁板中心位移更接近，因而释放该约束可得到更准确的结果。

(3) 释放舱壁板4边的3个转角自由度UR1、UR2、UR3约束，保留3个位移自由度约束，舱壁板的最终变形云图如图8所示，最终时刻舱壁板中心位移为359.0 mm。

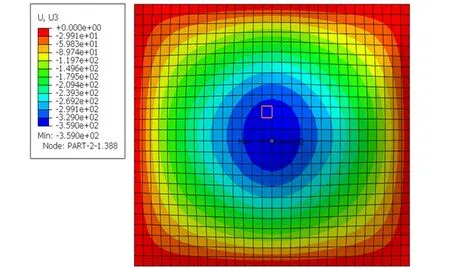
图8 释放UR1、UR2、UR3的约束后 舱壁板的最终变形云图

释放UR1、UR2、UR3的约束后舱壁板中心位移与释放UR1和UR2的约束后舱壁板中心位移一致，这验证了上述的推论，即释放UR3的约束对舱壁板中心位移几乎没有影响。

2.4 计算结果分析

不同边界条件及相应的舱壁板中心位移如表1所示，在计算不同边界条件下舱壁板中心位移的误差时以从完整舱室结构模型所得到的舱壁板中心位移作为基准。

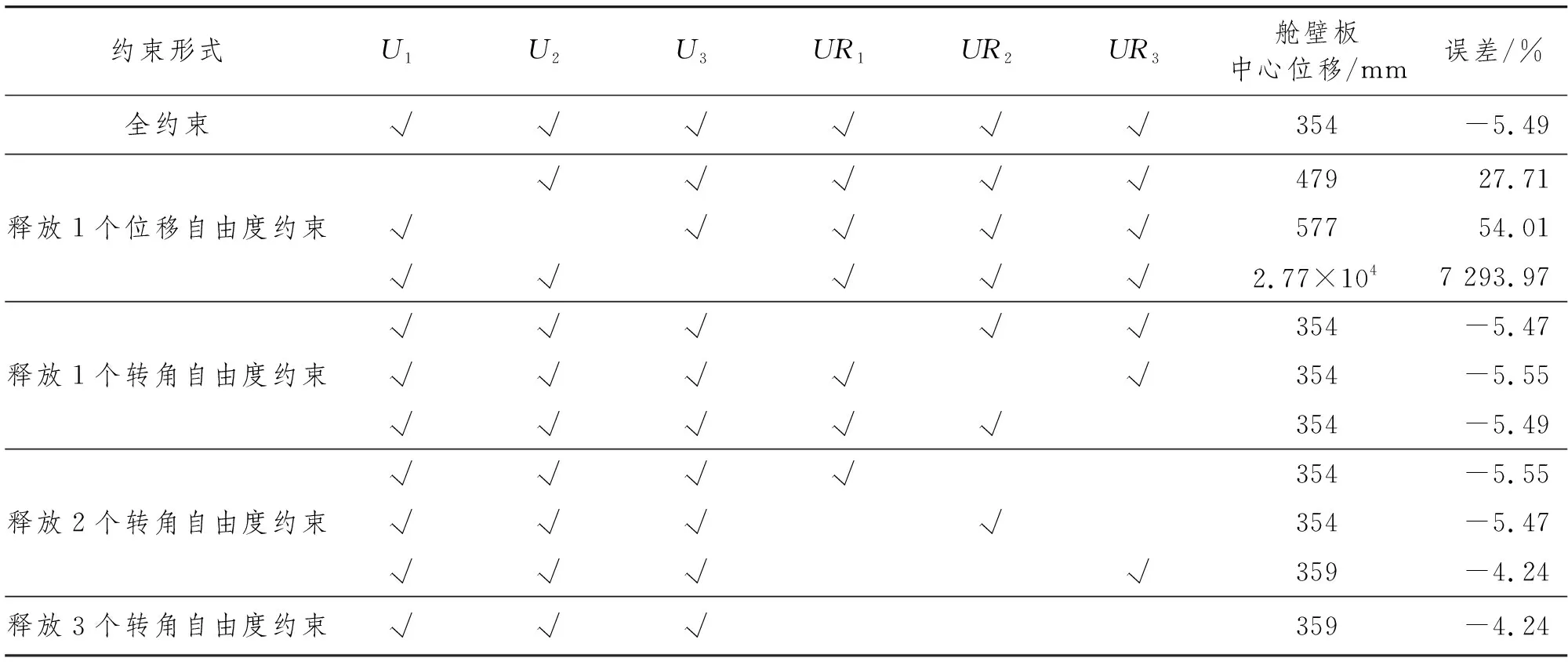
表1 不同边界条件及相应的舱壁板中心位移

如表1所示：释放舱壁板4边的3个转角自由度约束、保留3个位移自由度约束是最合理的边界条件；释放舱壁板4边的转角自由度约束对舱壁板中心位移影响较小；释放舱壁板4边的转角自由度约束的各种边界条件下的舱壁板中心位移变形可用正弦函数y=Asin(Bx+C)+D表示，式中x为时间，参数A为位移幅值，参数B为角速度，参数C为初相，参数D为平衡位置的位移量。该分布曲线通过Origin软件拟合出对应的函数，结果如表2 所示。

由表2可知：转角自由度约束对舱壁板变形拟合函数的影响较为明显，对参数B、参数C和参数D的影响甚微，对参数A有显著的影响。

为研究舱壁板的长宽比及分别释放U1和U2的约束对舱内爆炸载荷作用下舱壁板动力响应的影响，保持舱室(舱壁板)长度、高度及TNT当量不变，改变舱室(舱壁板)宽度。不同长宽比时由完整舱室结构模型得到的舱壁板中心位移及分别释放U1和U2的约束后得到的舱壁板中心位移如表3所示。

[][]

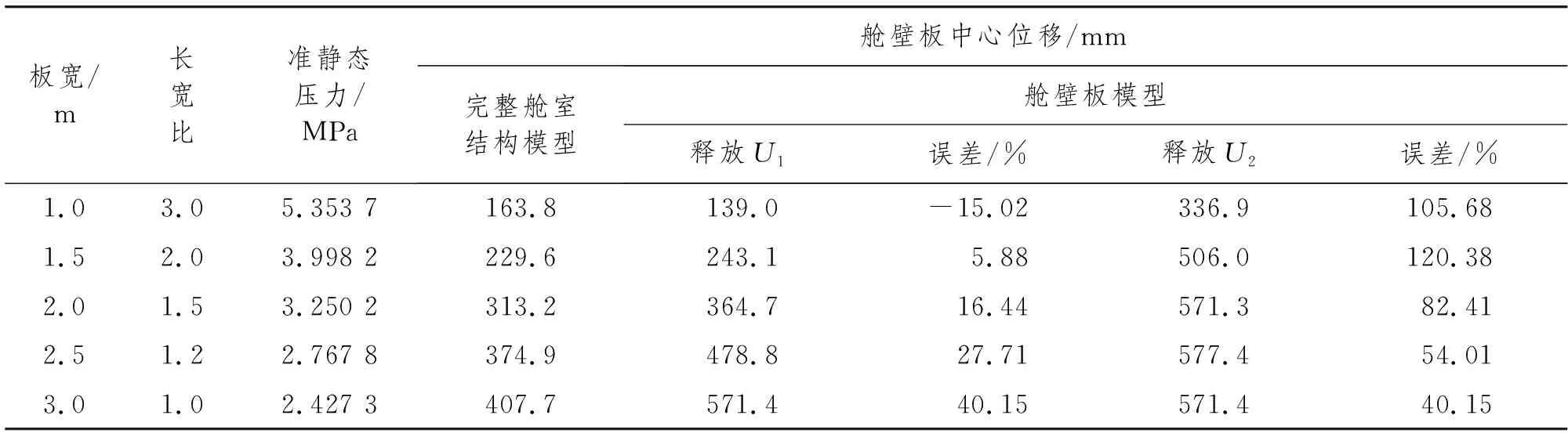
表3 不同长宽比时2种模型舱壁板中心位移

如表3所示：舱壁板的长宽比对舱壁板中心位移有很大的影响，当长宽比在2.0左右时，释放U1的约束后得到舱壁板中心位移的误差最小，但释放U2的约束后得到舱壁板中心位移的误差最大。

3 结 论

舰船在现代海战中是主要的受攻击对象，对舱室在爆炸载荷作用下舱壁板的动力响应进行研究具有重大意义和军用价值。传统流固耦合的方法计算量大、耗时长，故基于通用有限元软件Abaqus建立完整的舱室结构模型和几种舱壁板模型，运用一种新的简化计算方法，通过分析几种具有不同边界条件的舱室舱壁板模型，研究舱内爆炸载荷作用下舱壁板的动力响应，所得数值计算结果可为相关研究提供参考。结论归纳如下：

(1) 对舱壁板模型而言，释放舱壁板4边的3个转角自由度约束、保留3个位移自由度约束是最合理的边界条件。

(2) 舱壁板的长宽比对舱壁板中心位移的影响较为显著。

(3) 释放舱壁板4边的转角自由度约束对舱壁板中心位移的影响甚小。