可分离变量微分方程案例教学的探索与实践

潘 花，仇海全

可分离变量微分方程案例教学的探索与实践

潘 花，仇海全

（安徽科技学院 信息与网络工程学院，安徽 蚌埠 233030）

微分方程这部分内容比较抽象、逻辑性较强、概念多，难度较大。在教学过程中采用案例教学法，将枯燥的概念讲解、方程解法练习融入到实际案例分析中，能够激发学生的学习积极性，提高教学效果。

新冠肺炎；微分方程；SI模型

微分方程是《高等数学》知识体系的一个重要组成部分，这部分内容具有概念多、方程类型多、抽象性强等特点。为激发学生的学习兴趣，提高教学效果，采用案例教学法讲解可分离变量微分方程。将新冠肺炎疫情分析和预测作为教学案例，将抽象的理论知识与实际问题结合起来，建立数学模型。探讨了利用微分方程模型预测新冠肺炎疫情发展的方法，并将其融入到课程教学中，遵循“学生中心”教学理念[1]，注重课程思政。不仅能有效激发学生的学习兴趣、提高学习热情，还有利于提高学生解决实际问题的能力、创新能力和科研能力[2]。

1 建立数学模型

新冠肺炎对人们的生产、生活产生了重大影响，以新冠肺炎疫情为教学案例，通过分析建立其数学模型，进而引入新课。

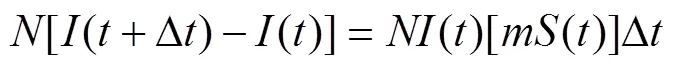
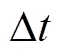
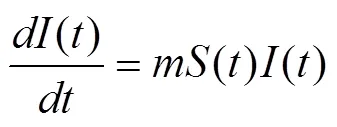
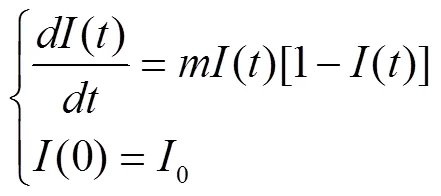
该模型称为SI传染病模型[3]。通过建立数学模型，把实际问题转化为微分方程问题。

2 结合案例，引出新课

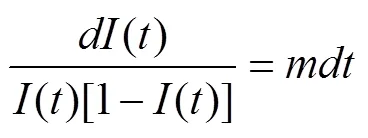
通过对实际问题进行建模和分析，能够直观形象地给出可分离变量微分方程的概念，便于学生理解和掌握。

由上面的定义可知，SI模型中的微分方程是可分离变量微分方程，若要对模型进行求解，需要掌握可分离变量微分方程的具体求解步骤[4]。

可分离变量微分方程的求解步骤：

在对微分方程进行变形时，要特别注意是否有增根、减根的情况。

应用上述步骤求解SI模型中的一阶微分方程初值问题，在练习中巩固所学知识和方法，提升应用所学知识解决实际问题的能力。

所求初值问题的特解为：

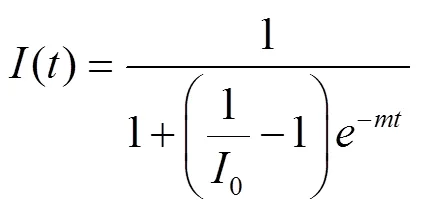
3 模型分析与预测

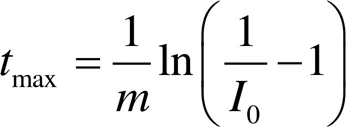
图1 与之间的函数关系图

图2 的图像

SI模型只考虑了传染病爆发和传播的过程，而没有考虑确诊病人治愈恢复健康的过程。由于该模型的假设条件过于理想化、简单化，并不能真实反映传染病的发展趋势，但是该模型具有重要的现实意义。

从世界卫生组织网站[6]选取2020年1月21日至2020年5月17日中国新冠肺炎疫情统计数据。首先利用四点法估计，再利用线性回归估计和的值[7]。实际数据和预测结果如图3所示。由图3可以看出，在党和政府的领导下，我国采取积极有效的防控措施，经过医护人员的不懈努力和全体中国人民的不懈奋斗，取得了抗击新冠肺炎疫情的重大胜利。

通过讲解实际问题，引导学生积极思考[8]。不仅能够凸显知识的重要性、提高学生应用知识的意识、激发学生的求知欲，还能让学生更深刻地认识当前疫情状况，对学生进行思想政治教育，激发学生的爱国热情，树立强烈的民族自豪感和自信心。

4 模型拓展，激发学生求知欲

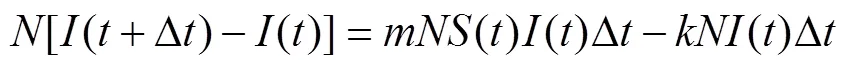
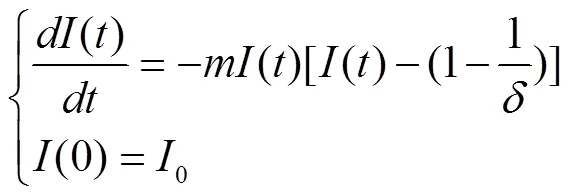
该模型称为SIS模型，该微分方程也可利用分离变量法进行求解。传染病模型除了SI、SIS模型外，还有SIR、SIRS、SEIR[9]等传染病模型。

通过介绍其他传染病模型，拓展学生的知识面，鼓励学生课下查资料了解其他传染病模型，激发学生的求知欲和探索意识。

结束语

《高等数学》课程的重要性不言而喻[10]，为了获得更好的教学效果，激发学生的学习兴趣，提高学生的数学素养[11]，教学过程中必须注重理论知识与实际问题相结合。将理论知识与实际问题紧密结合，采用直观形象的案例教学方法能够激发学生的学习兴趣和求知欲。在多样性、实践性的学习过程中，让学生既动脑又动手，强化对所学知识的理解，提高应用数学知识分析和解决问题的能力，有利于培养创新型人才。

[1] 李虹瑾, 朱雅琳. 高校“学生中心”教学改革的阻力与突破[J]. 宜宾学院学报, 2019, 19（8）: 117~125.

[2] 高海音, 祝英杰. 将数学建模思想融入常微分方程教学的探索与实践[J]. 长春大学学报, 2012, 22（12）: 1543~1546.

[3] 葛清, 冀桂琳, 李盈科, 等. 随机SI传染病模型的概率分析[J]. 统计与决策, 2017（7）: 21~24.

[4] 同济大学数学系. 高等数学: 第七版[M]. 北京: 高等教育出版社, 2014: 302~305.

[5] 赵文英, 袁赫. 基于改进Logistic模型的中国社会消费品零售总额预测[J]. 牡丹江师范学院学报（自然科学版）, 2018, 105（4）: 15~18.

[6] World Health Organization. “Coronavirus disease (COVID-2019) situation reports”[R/OL]. [2020-05-18]. https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports/.

[7] 宋之杰, 唐晓莉. 基于Logistic模型的我国信息产业演化发展研究[J]. 数学的实践与认识, 2019, 49（5）: 151~159.

[8] 潘花, 仇海全. 极坐标系下的面积元素推导[J]. 重庆科技学院学报（自然科学版）, 2018, 20（6）: 110~112.

[9] 李昊, 段德光, 陶学强, 等. 传染病动力学模型及其在新型冠状病毒肺炎疫情仿真预测中的应用综述[J]. 医疗卫生装备, 2020, 41（3）: 7~12.

[10] 潘花, 仇海全. 基于“超星学习通平台”的《高等数学》混合教学模式的探索[J]. 黑河学院学报, 2020（3）: 100~102.

[11] 林伟华. 分析与启示: 数学素养和数学核心素养的关系[J]. 牡丹江师范学院学报（自然科学版）, 2018, 105（4）: 60~65.

Exploration and Practice of Case Study Mode in Differential Equations with Separable Variables

PAN Hua，QIU Hai-quan

(College of Information and Network Engineering, Anhui Science and Technology University, Bengbu Anhui 233030, China)

Differential equation is difficult to learn due to its relatively abstract yet abundant concepts, and strict logic. The case study method is adopted in the teaching process, integrating the dull concept explanation and equation solving exercises into the actual case analysis, therefore stimulating students’ enthusiasm for learning and improving the teaching effect.

COVID19; differential equation; SI model

2020-05-21

安徽省教育厅自然科学研究重点项目（KJ2019A0816）；安徽省高等学校省级质量工程项目（2018jyxm0671）

潘花（1980—），女，山东泗水人，讲师，硕士，研究方向：计算机辅助几何设计、高等数学教学。

O172

A

2095-9249（2020）03-0102-05

〔责任编校：吴侃民〕