跳过程驱动的随机时滞微分方程的指数稳定性

王 珊

跳过程驱动的随机时滞微分方程的指数稳定性

王 珊

（萍乡学院 工程与管理学院，江西 萍乡 337000）

文章研究了一类跳过程驱动的时滞随机微分方程的稳定性。利用Banach不动点定理和一些不等式得到了在一定条件下，Mild解存在且是均方指数稳定的。

随机发展方程；Lévy跳过程；Mild解；指数稳定性

引言

随机（偏）微分方程用来刻画一个系统的变化过程，在数学、经济、金融、工程等领域有着广泛的应用，其解的存在性、唯一性、稳定性等渐近性质得到广泛的研究[1~4]。Zhang-Chen[3]研究了带Markov切换的随机时滞微分方程全局解的存在唯一性、具有一般衰减函数的p阶矩和几乎必然指数稳定性。Ji等[4]研究了具有有限或可数状态空间的带切换和跳扩散过程的稳定性问题。关于随机微分方程的系统知识和理论可以见文献[5~7]。

众所周知，生活中充满了各种各样随机因素的干扰。一般地，Brown运动刻画连续轨道的随机扰动。但是当一些随机干扰非常剧烈时，这种干扰会使系统在短时间内发生不连续的变化。因此，Brown运动刻画的随机因素对这类现象的描述会有一点局限，研究者们用Lévy跳过程来表示这类不连续的变动。Lévy过程驱动的随机微分方程在排队论、保险风险、数理金融等领域有着重要的应用，其性质得到了广泛的研究[8~10]。Zhu[10]利用反证法研究了一类Lévy过程驱动的随机时滞微分方程，得到了方程稳定的充分条件。

Banach不动点定理是泛函分析中重要的定理之一。很多学者利用此定理来研究微分方程的稳定性[11~12]。本文将利用不动点定理来研究如下的Lévy跳过程驱动的随机时滞微分方程的指数稳定性：

1 背景知识

我们先介绍一些背景知识、假设和引理。

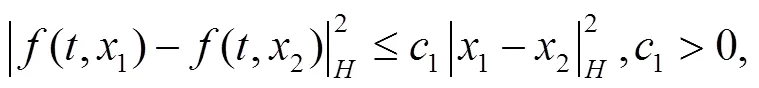
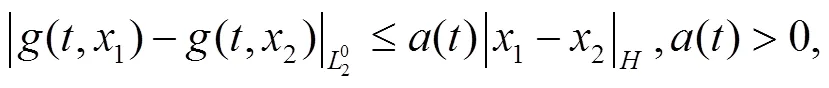
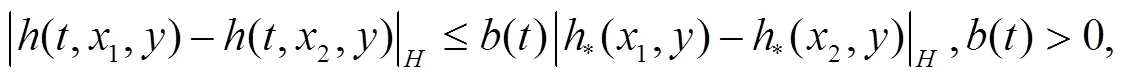
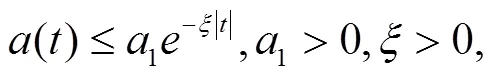
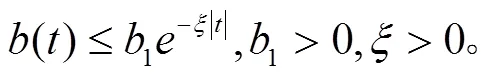
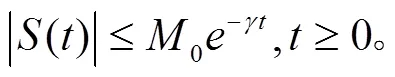
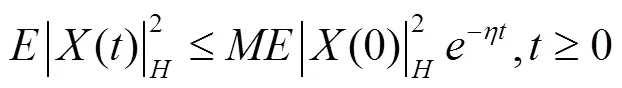
2 方程的指数稳定性

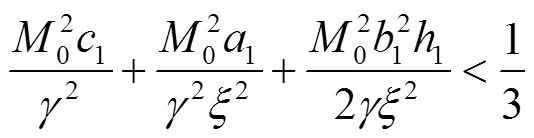
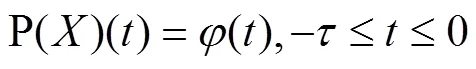
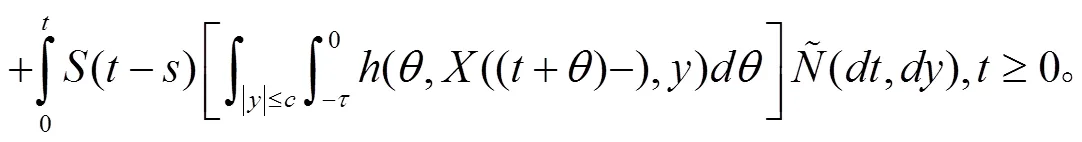
因此可以得到：

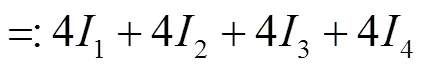
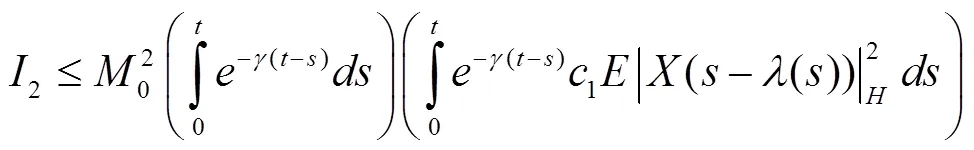
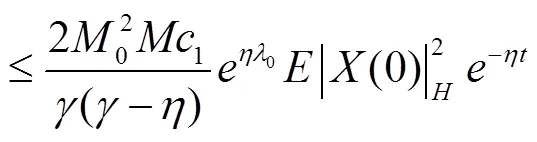
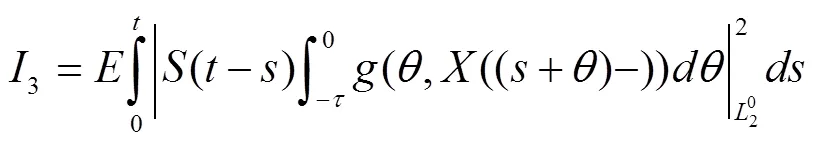
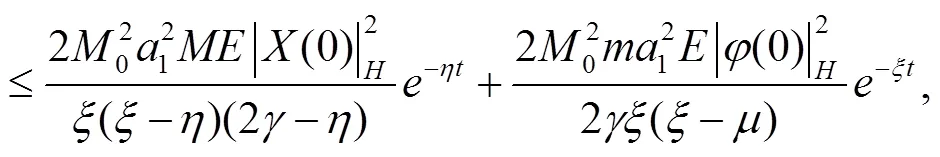
根据式（4）、式（7），有

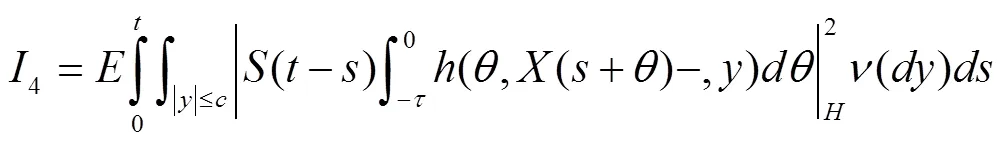
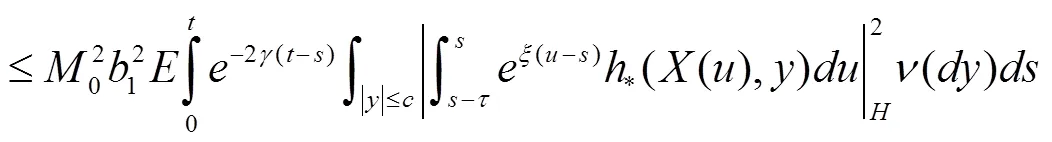
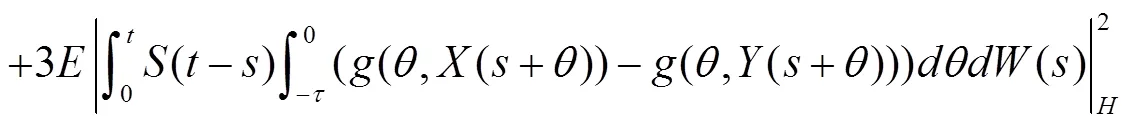
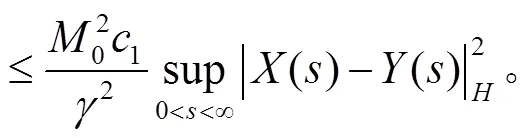
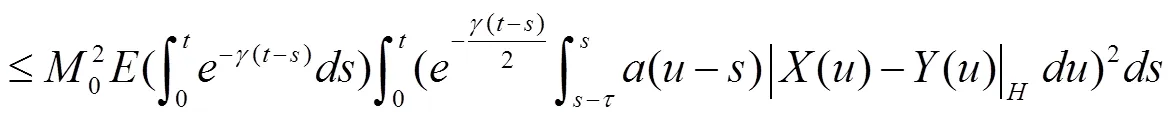
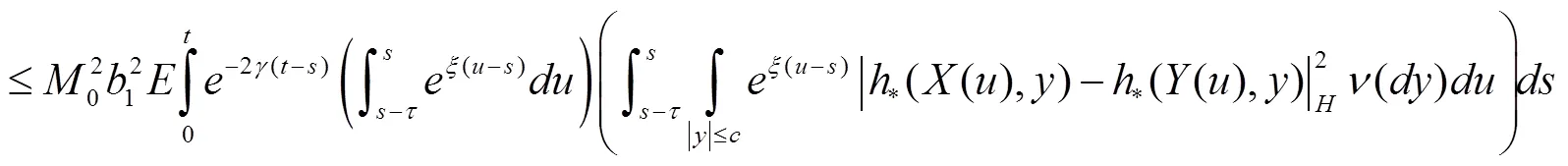
[1] T. Taniguchi. Asymptotic stability theorems of semilinear stochastic evolution equations in hilbert spaces[J]. Stochastics, 1995, 53: 1~2, 41~52.

[2] D. Li, S. Liu, J. Cui. Threshold dynamics and ergodicity of an SIRS epidemic model with semi-Markov switching[J]. J. Differential Equations, 2019, 266: 3973~4017.

[3] T. Zhang, H.B. Chen. The stability with a general decay of stochastic delay differential equations with Markovian switching[J]. Appl. Math. Comput., 2019 359: 294~307.

[4] H.J. Ji, J.H. Shao, F.B. Xi. Stability of regime-switching jump diffusion processes[J]. J. Math. Anal. Appl. 2020, 484: 123727.

[5] X. Mao. Stochastic Differential Equations and their Applications[M]. Horwood Publishing, Chichester, 2007.

[6] X.R. Mao, C.G. Yuan. Stochastic Differential Equations with Markovian Switching[M]. London, Imperial College Press, 2006.

[7] G. Da Prato and J. Zabczyk. Stochastic Equations in Infinite Dimensions[M]. Cambridge University Press, Cambridge, 2014.

[8] J.W. Luo, K. Liu. Stability of infinite dimensional stochastic evolution equations with memory and Markovian jumps[J]. Stochastic Process. Appl., 2008, 118: 864~895.

[9] T. Taniguchi. The existence and asymptotic behaviour of solutions to non-Lipschitz stochastic functional evolution equations driven by Poisson jumps [J]. Stochastics, 2010, 82(4): 339~363.

[10] Q.X. Zhu. Stability analysis of stochastic delay differential equations with Lévy noise[J]. Syst. Control Lett., 2018, 118:62~68.

[11] L. Wei, Q.X. Zhu et.al. p-th moment exponential stability of hybrid stochastic fourth-order parabolic equations [J]. Adv. Difference Equ., 2016, 2016: 65.

[12] J.W. Luo, T. Taniguchi. Fixed Points and Stability of Stochastic Neutral Partial Differential Equations with Infinite Delays[J]. Stoch. Anal. Appl., 2009: 27(6): 1163~1173.

Exponential Stability of Stochastic Delay Differential Equations Driven by Jump Processes

WANG Shan

(School of Management and Engineering, Pingxiang University, Pingxiang Jiangxi 337000, China)

In the paper, the stability of a class of stochastic delay differential equations driven by Lévy jump processes is studied. By making use of Banach fixed point theorem and some inequality techniques, the Mild solution is obtained and is exponentially stable under certain conditions.

stochastic evolution equation; Lévy jump processes; Mild solution; exponential stability

2020-06-18

萍乡学院青年科研基金项目（2018D0224）

王珊（1987—），女，江西萍乡人，讲师，硕士，研究方向：随机微分方程及其应用。

O211.63

A

2095-9249（2020）03-0001-06

〔责任编校：范延琛〕