基于演化博弈的偶发性强刺激对安全行为作用研究
李春林 谭钦文 文宣 吴春燕 卢智渊 章少康
(西南科技大学 四川绵阳 621010)
0 引言
根据人的社会属性行为模式,行为由动机支配,而动机由需求产生[1-2]。作为企业的雇员,从经济性角度考虑,工人和安全管理人员的需求就是工作过程及其结果所带来的收益,而动机则是获得更高的收益。
博弈论是预测一定理性状态下博弈参与者为获得更高收益所采取行为的一种工具,常用于研究具有斗争或竞争性质的现象,公式化了一定制度下博弈双方的相互作用规律[3]。其中,演化博弈理论认为博弈参与者有限理性,并且达成均衡需要一定的演化过程,演化过程中收益较低者会学习收益较高者的策略。
演化博弈中的均衡称为演化均衡(EE),而演化均衡中的稳定均衡称为演化稳定策略(ESS)[4]。求出演化稳定策略就能在一定程度上预测模拟一个企业中工人和安全管理人员稳定状态下的博弈情况。在以往关于企业安全管理的演化博弈研究中,研究往往只局限于个别几个演化博弈种类,且未对偶发性强刺激作用进行研究[5-7],因此本研究不仅可以模拟博弈情况,对企业安全工作作出指导建议,还能补充现有理论研究的不足。
1 博弈参数设置及博弈类型
不同于传统博弈,演化博弈中涉及到的计算要素除了博弈参与者、行动策略和收益外还有初始博弈策略的概率。在企业安全管理的演化博弈中,博弈参与者为工人和安全管理人员;工人有遵章守纪和违规违章两种行动策略,安全管理人员有认真监管和监管懈怠两种行动策略,遵章守纪和认真监管属于安全行为,违规违章和监管懈怠属于不安全行为;各个博弈局面收益数值的大小关系决定了博弈的种类;初始行动策略的概率又在博弈种类的基础上决定了演化博弈的具体演化过程[8]。
1.1 参数设置及演化均衡
在企业安全管理的博弈中,工人和安全管理人员两种策略两两组合会形成4种博弈收益局面。为计算便捷起见,综合叠加各类收益因素,设工人的收益分别为W11,W12,W21,W22,安全管理人员的收益分别为S11,S12,S21,S22,以W11和S11为例,这两个数值分别表示了安全管理人员认真监管且工人遵章守纪情况下工人和安全管理人员的收益;工人遵章守纪的概率为p,不遵章守纪的概率为1-p;安全管理人员认真监管的概率为q,监管懈怠的概率为1-q,则博弈收益矩阵如下表1所示。

表1 博弈收益矩阵
设工人群体中遵章守纪的工人收益为U1,违规违章的收益为U2,则
U1=qW11+(1-q)W12
(1)
U2=qW21+(1-q)W22
(2)
工人群体的平均收益为
(3)
根据复制动态方程的定义,工人选择遵章守纪行为的复制动态方程为
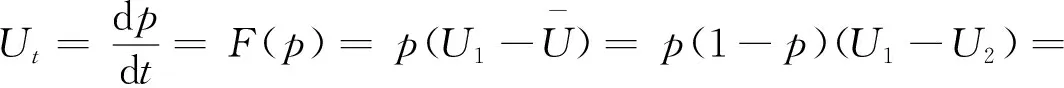
(4)
同理,可以得出安全管理人员选择认真监管行为的复制动态方程为
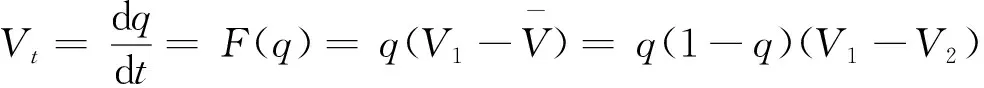
(5)
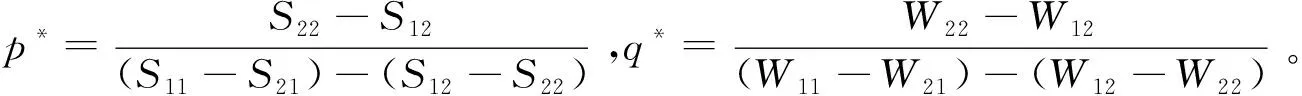
1.2 博弈类型及存在的可能性
通过判断复制动态方程所组成的雅克比矩阵的行列式和迹的正负性可以判断演化均衡是否是演化稳定策略。见表2,如果雅克比矩阵的行列式为正,迹为负,则该演化均衡点为演化稳定策略;如果雅克比矩阵的行列式为正,迹为正,则该演化均衡点为不稳定点;如果雅克比矩阵的行列式为负,则无论迹正负,该均衡点均为鞍点[7]。
企业安全管理博弈的雅克比矩阵如下所示:
(6)

表2 各均衡点雅克比矩阵的行列式和迹
结合上表2,不考虑收益相等的极端情况,W11与W12,W21与W22,S11与S12,S21与S22这4对收益的大小关系决定了演化博弈的种类,因此理论上会存在24种演化博弈。通过判断雅克比矩阵行列式和迹的正负,这16种博弈可以按照演化稳定策略的个数分为3类。
(1)第1类,不存在演化稳定策略的博弈(即E点为演化中心),可细分为两种,工人和安全管理人员的收益大小关系分别为W11>W21,W22>W21,S21>S11,S12>S22或者W11 (2)第2类,只存在一个演化稳定策略的博弈,可细分为4小类12种。 ①第1小类的演化稳定策略为工人遵章守纪且安全管理人员认真监管(即D点),其收益大小关系有3种,演化趋势相同,但是具体意义不同,分别为W11>W21,S11>S21,W12>W22,S12>S22;W11>W21,S11>S21,W22>W12,S12>S22;W11>W21,S11>S21,W12>W22,S22>S12。其中第3种收益情况:工人选择违规违章时安全管理人员选择认真监管的收益低于监管懈怠,同时,工人选择遵章守纪时认真监管收益高于监管懈怠的收益,不符合实际,应予以舍去。 ②第2小类的演化稳定策略为工人不遵章守纪且安全管理人员监管懈怠(即A点),其收益大小关系有3种,演化趋势相同,但是具体意义不同,分别为W22>W12,S22>S12,W21>W11,S21>S11;W22>W12,S22>S12,W11>W21,S21>S11;W22>W12,S22>S12,W21>W11,S11>S21。其中第3种收益情况:工人选择违规违章时安全管理人员选择认真监管的收益低于监管懈怠,同时,工人选择遵章守纪时认真监管收益高于监管懈怠的收益,不符合实际,应予以舍去。 ③第3小类的演化稳定策略为工人遵章守纪且安全管理人员监管懈怠(即B点),其收益大小关系有3种,演化趋势相同,但是具体意义不同,分别为W12>W22,S21>S11,W11>W21,S22>S12;W12>W22,S21>S11,W11>W21,S12>S22;W12>W22,S21>S11,W21>W11,S22>S12。其中第3种收益情况:安全管理人员选择认真监管时工人的违规违章收益高于遵章守纪收益,同时,安全管理人员选择监管懈怠时工人的违规违章收益低于遵章守纪收益,不符合实际,应予以舍去。 ④第4小类的演化稳定策略为工人不遵章守纪且安全管理人员认真监管(即C点),其收益大小关系有3种,演化趋势相同,但是具体意义不同,分别为W21>W11,S12>S22,W22>W12,S11>S21;W21>W11,S12>S22,W12>W22,S11>S21;W21>W11,S12>S22,W22>W12,S21>S11。其中第3种收益情况:安全管理人员选择认真监管时工人的违规违章收益高于遵章守纪收益,同时,安全管理人员选择监管懈怠时工人的违规违章收益低于遵章守纪收益,这种情况是不符合现实的,应予以舍去。 (3)第3类,存在两个演化稳定策略的博弈,可细分为两种。第1种的演化稳定策略为“工人选择遵章守纪同时安全管理人员认真监管”和“工人选择违规违章同时安全管理人员监管懈怠”(即A,D点),其收益大小关系为W11>W21,S11>S21,W22>W12,S22>S12;第2种的演化稳定策略为“工人选择不遵章守纪同时安全管理人员认真监管”和“工人选择违规违章同时安全管理人员监管懈怠”(即B,C点),其收益大小关系为W21>W11,S12>S22,W12>W22,S21>S11。在第2种博弈收益情况中,安全管理人员监管懈怠时工人遵章守纪收益高于不遵章守纪收益,同时,安全管理人员选择认真监管时工人的违规违章收益高于遵章守纪收益,这种情况显然不符合人性和实际,应予以舍去。 所以,企业安全管理中的演化博弈可按演化稳定策略的个数分为3类,并结合实际情况进一步分为10种。 企业的工人和安全管理人员在生产过程中有受到偶发性强刺激作用(如发生安全事故、政府机构突击检查等)的可能,强刺激发生带来的威慑警醒作用能够立即改变不同博弈局面的收益大小,提升工人遵章守纪和安全管理人员认真监管的概率。但是这种安全上的威慑警醒作用往往会随着时间衰退,最后恢复成原先水平。 通过MATLAB软件模拟,发现第2类博弈在强刺激作用后,演化的结果均会恢复成原先的演化稳定策略。另外,由演化博弈规则和模拟结果可知,在第2类博弈中同一小类的演化博弈其演化趋势和结果是相同的,因此不再细分模拟。 设t=10时发生强刺激,强刺激作用下工人和安全管理人员的博弈收益突变为W11=5,S11=5,W12=5,S21=-5,W21=-5,S12=5,W22=-5,S22=-5;安全收益常规时间段t1∈[0,10),t3∈[15,50),安全强刺激作用恢复时间段t2∈[10,15),期间工人和安全管理人员的收益匀速恢复成常规收益;设初始工人遵章守纪概率p=0.7,安全管理人员认真监管概率q=0.8,强刺激作用后工人遵章守纪概率突变为0.99,安全管理人员认真监管的概率突变为0.99。 第2类博弈中第1小类由于在强刺激作用前双方的遵章守纪和认真监管的概率已经趋于1,所以强刺激并不会将概率降低为0.99,而是保持为1。设初始W11=3,W12=3,W21=-4,W22=2,S11=3,S21=2,S12=4,S22=-4,则博弈过程如图1所示。 图1 第2.1类博弈演化 第2类博弈中第2小类由于在强刺激作用前双方的遵章守纪和认真监管的概率已经趋于0,所以强刺激会将双方概率突增为0.99。设初始W11=-1,W12=-1,W21=0,W22=4,S11=2,S21=3,S12=3,S22=5,则博弈过程如图2所示。 图2 第2.2类博弈演化 第2类博弈中第3小类由于在强刺激作用前工人和安全管理人员的遵章守纪和认真监管的概率分别趋于1和0,所以强刺激作用后概率突变为1和0.99。设初始W11=3,W12=3,W21=-4,W22=2,S11=3,S21=2,S12=4,S22=-4,则博弈过程如图3所示。 图3 第2.3类博弈演化 第2类博弈中第4小类由于在强刺激作用前工人和安全管理人员的遵章守纪和认真监管的概率分别趋于0和1,所以强刺激作用后概率突变为0.99和1。设初始W11=1,W12=1,W21=4,W22=5,S11=4,S21=2,S12=4,S22=1,则博弈过程如图4所示。 图4 第2.4类博弈演化 2.2.1 演化轨迹改变的博弈 第1类博弈中工人和安全管理人员的安全行为概率循环波动,设定强刺激作用后双方概率突增为0.99,设初始W11=3,W12=3,W21=-4,W22=4,S11=3,S21=5,S12=4,S22=-4,t1∈[0,30),t3∈[35,90),t2∈[30,35),则博弈过程如图5所示。在强刺激作用消退后,双方仍然维持了一定时间的安全行为概率,但是最后还是恢复成循环波动的状态,且波动幅度比原先更大。 图5 第1类博弈演化 2.2.2 演化稳定策略位置改变的博弈 第3类博弈由于有两个演化稳定策略,所以需要分两种情况,按照初始双方行为概率大小不同进行分析。设W11=0,W12=0,W21=-3,W22=4,S11=4,S21=3,S12=3,S22=4,t1∈[0,10),t3∈[15,50),t2∈[10,15)。在初始p,q值综合较高的情况下,如p,q值分别为0.7,0.8时,强刺激作用前工人和安全管理人员的遵章守纪和认真监管的概率均已经趋于1,则博弈过程如下图6所示。 图6 第3类博弈(高p,q值)演化 在初始p,q值综合较低的情况下,如p,q值分别为0.3,0.4时,强刺激作用前工人和安全管理人员的安全行为的概率均已经趋于0,所以强刺激作用后概率突变为0.99。博弈过程如下图7所示,在强刺激作用消退后,工人和安全管理人员的行为概率维持为1的水平不变。 图7 第3类博弈(低p,q值)演化 通过以上模拟分析可以发现,强刺激确实能起到一定的提升安全行为概率的作用,但是对于大多数博弈种类来说这种作用并不长久。 对于第2类博弈来说,随着时间增加,强刺激作用消失,博弈收益恢复成原先水平,双方行为概率,即演化稳定策略也会恢复成原先状态,但是行为概率恢复所需的时间要大于刺激作用消退所需时间。对于第1类博弈来说,随着时间增加,强刺激作用消失,博弈收益恢复成原先水平,演化博弈中博弈双方的行为概率恢复了波动性,但是经过刺激后,工人p值下限变低,安全管理人员q值上限变高,双方行为概率的波动增大。对于第3类博弈来说,强刺激作用可以使得原先初始p,q值综合较低的博弈的演化稳定策略从(0,0)变为(1,1),且这种改变能长期维持。 偶发性的强刺激是一种短期的、作用效果较强的激励,不存在固定的周期。根据遗忘消退说和遗忘压抑说,强刺激不重复出现,威慑警醒作用会得不到强化而渐渐消退,原先压抑的不安全动机也会得到释放。综上,对企业提出3点建议来提升其安全水平: (1)通过提高安全奖惩金额,加强安全行为教育等各种长效的激励手段,改变工人和安全管理人员的行为策略收益,促使博弈收益向第2.1类靠近,改变博弈种类。 (2)结合实践经验,得出定期刺激周期,保证在工人和安全管理人员安全行为概率降低前进行刺激。 (3)对于存在第1类博弈情况的企业,偶发性强刺激手段应谨慎使用,避免行为概率波动的增大;对于存在第3类博弈情况的企业,偶发性强刺激手段可以放心使用,尽早提升工人和安全管理人员安全行为的概率。 (1)通过比较企业工人和安全管理人员在不同策略组合下收益的大小关系可以确定理论上有16种演化博弈情况,但是结合企业安全生产实际,不同的博弈情况只可能存在10种,并可以按演化稳定策略的个数分为3类。 (2)通过MATLAB软件模拟发现,在强刺激作用消退后,大部分博弈中的工人和安全管理人员会恢复为原先的安全水平,甚至产生更多的违规违章和监管懈怠行为。 (3)企业可以通过对内部的工人和安全管理人员定期进行强刺激作用或者建立其他长效的激励机制来长期维持安全、合理的行为收益,进而保证企业的安全生产。2 偶发性强刺激作用下的演化博弈模拟
2.1 演化稳定策略不变的博弈


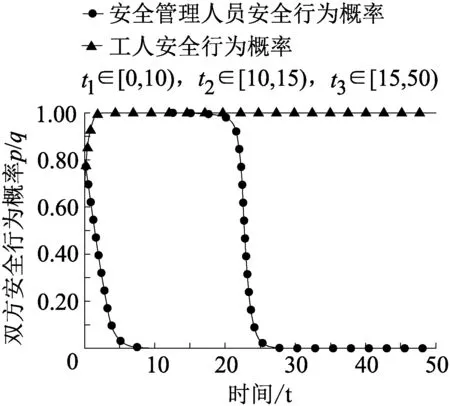
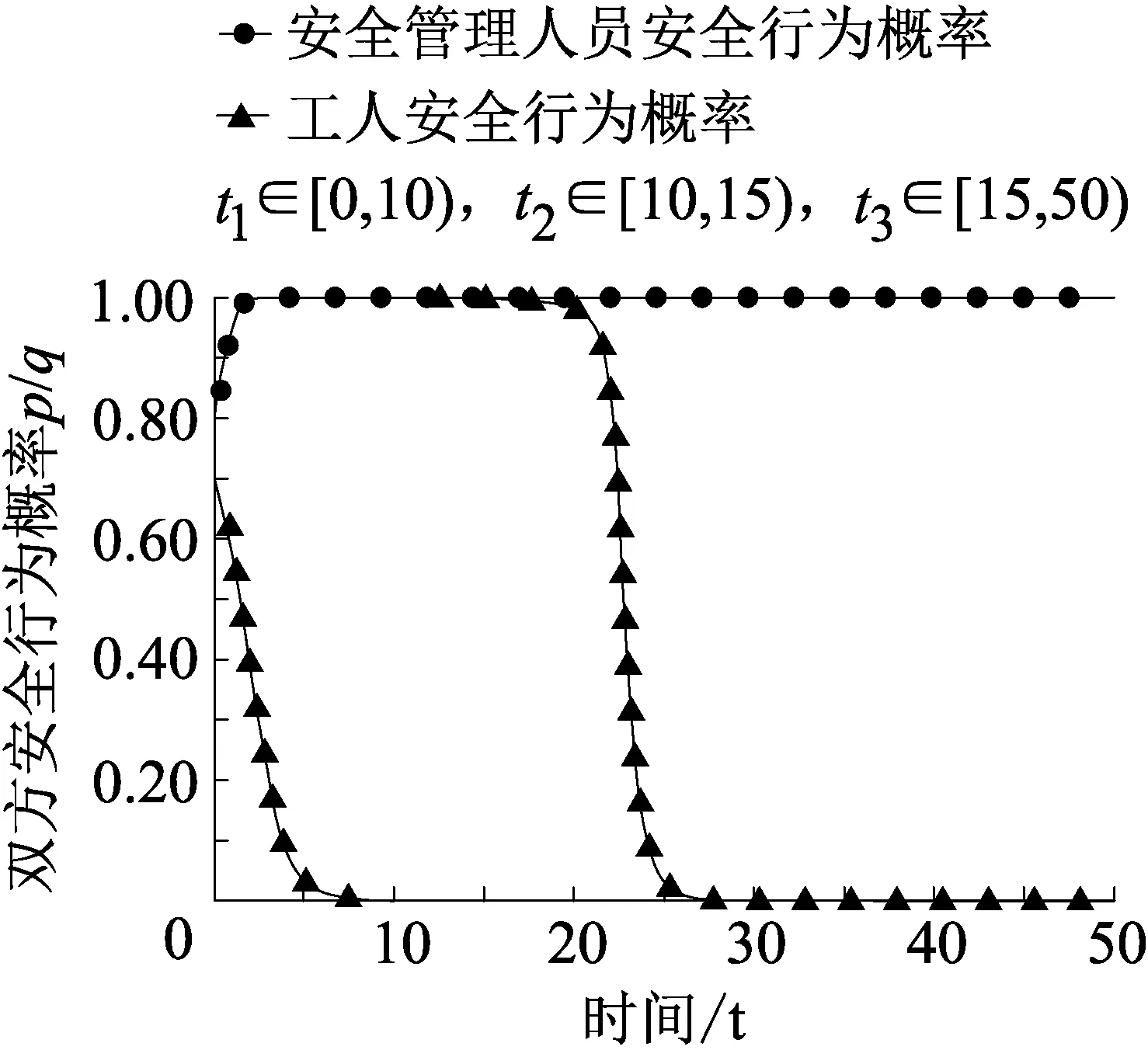
2.2 演化稳定策略发生改变的博弈
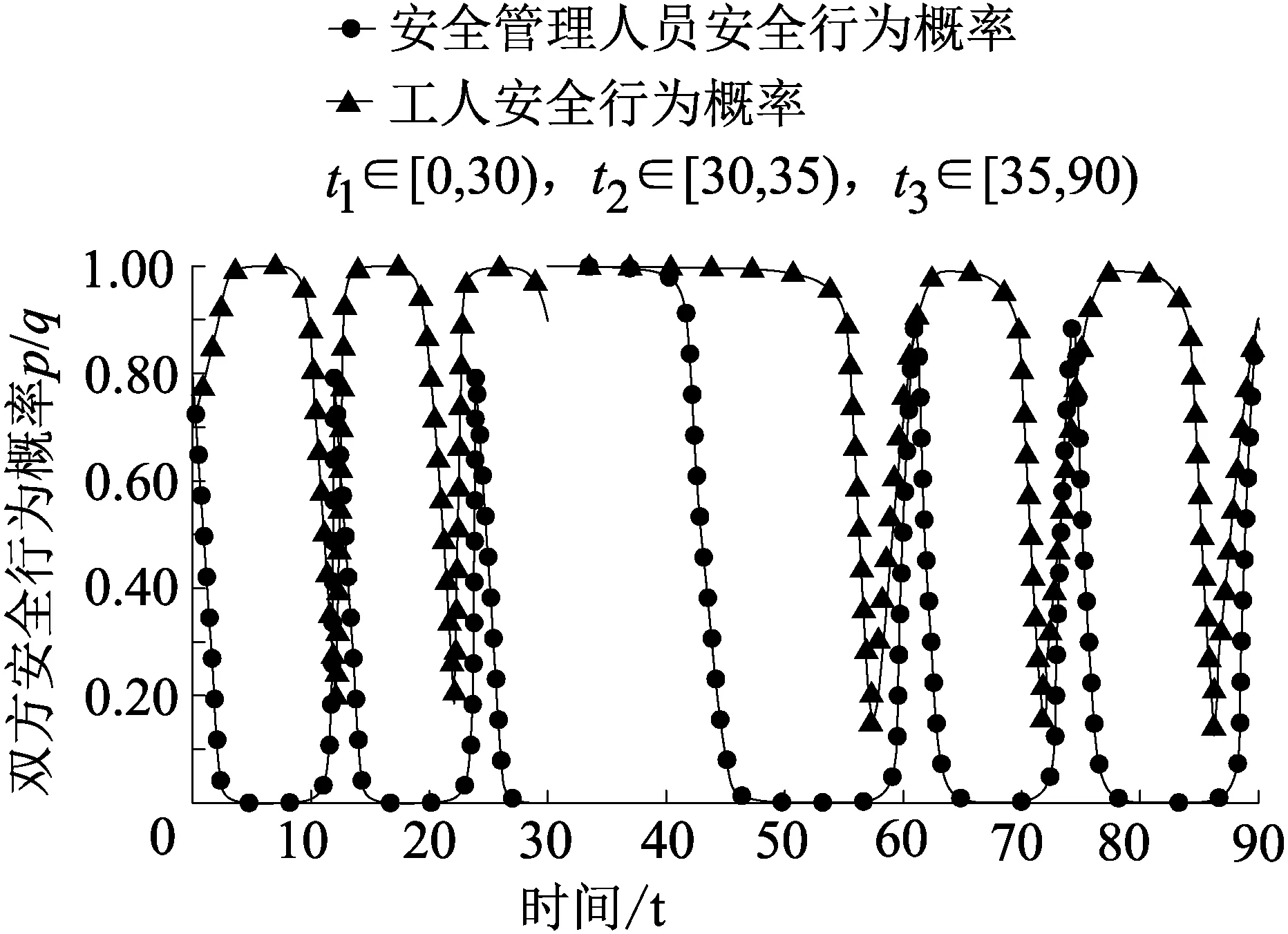
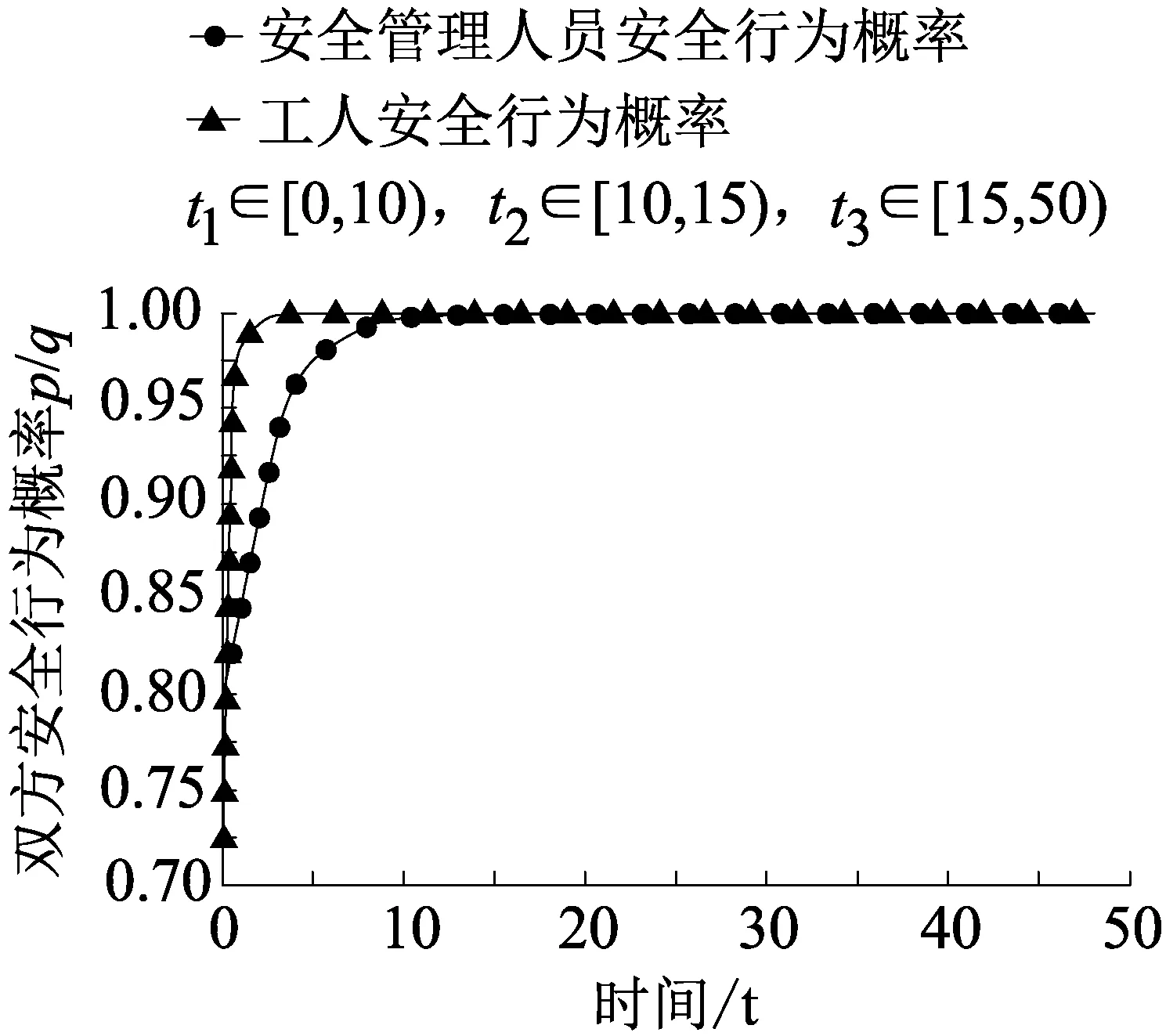

2.3 偶发性强刺激的影响规律与建议
3 结论

