一组波峰波谷实现光纤环镜传感器在线测量
江 莺,段 峥,张晓丽,胡兴柳
(1.南京林业大学 机械电子工程学院,南京 210037;2.信阳师范学院 物理电子工程学院,信阳 464000;3.金陵科技学院 智能科学与控制工程学院,南京 211169)
引 言
双折射光纤环镜(birefringence fiber loop mirror,Bi-FLM)传感器不仅可以作为可调谐光滤波器[1],还广泛应用于应变[2-5]、振动[6-7]、扭矩[8-9]等各类传感器。外界传感量的变化改变Bi-FLM传感器的干涉光谱,Bi-FLM传感器通过监测干涉光谱的变化来感知外界传感量。Bi-FLM传感器通常通过监测干涉光谱波长的变化来反推外界传感量的大小[10-18],即通过波长解调实现传感。波长解调的优点是不受光源强度波动影响,但波长解调的最大缺点是不能实现在线测量。作者根据Bi-FLM干涉光谱任意4个相邻波谷波长相对位置蕴含着应变信息的特点,曾研究通过任意4个相邻波谷波长及双折射光纤初始条件计算应变大小。该方法无需人为判断,有助于促进传感器与计算机有效对接,实现在线测量,但该方法需要4个相邻波谷的波长,包含3个周期的干涉波形,需要的信息量较多。双折射光纤长度越短,Bi-FLM干涉光谱周期越大[13],在一定的光源波长范围内,光纤长度较短的Bi-FLM可能没有足够的波谷点,导致无法计算。本文中提出通过一组相邻的波峰、波谷波长及双折射光纤初始条件计算应变大小,以此实现Bi-FLM应变传感器在线测量。该方法仅需0.5个周期的干涉波形,需要的信息量小,能够解决传感光纤长度较短的Bi-FLM传感器蕴含的信息量不足的问题。
1 理论分析
图1为Bi-FLM传感器原理图。将一根传统的单模3dB耦合器的端口3和端口4熔接一段双折射光纤作为传感元件,即构成Bi-FLM传感器。输入光源经端口1、光隔离器进入3dB耦合器,按1∶1分成从端口3顺时针和端口4逆时针相向传输的两束光,由于双折射光纤的双折射效应,最后两束光在端口2相遇并产生干涉。外界传感量的变化导致干涉光谱的变化,根据干涉光谱的变化,反推外界传感量的大小,以此实现传感。

Fig.1 Schematic of Bi-FLM
Bi-FLM传感器初始干涉光谱表达式为[19]:
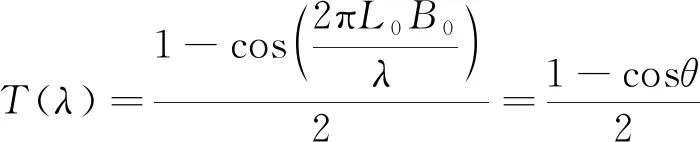
(1)
式中,λ为干涉光谱波长,T(λ)为干涉光谱强度,相角θ=2πL0B0/λ,L0为光纤初始长度,B0为光纤初始双折射率。
当双折射光纤受轴向应变后,相角变化量Δθ为[19]:

(2)
式中,εz=ΔL/L0=(L′-L0)/L0为双折射光纤轴向应变,单位为ε,其中L′为双折射光纤受应变后的长度;k是双折射应变系数,单位为1/ε,即光纤受1ε后双折射率变化大小。
由(2)式可得通过L′表示的Δθ表达式为:
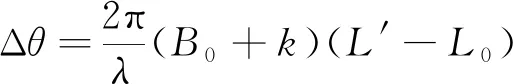
(3)
由(1)式、(2)式可得通过εz表示的受轴向应变后的Bi-FLM干涉光谱表达式为:
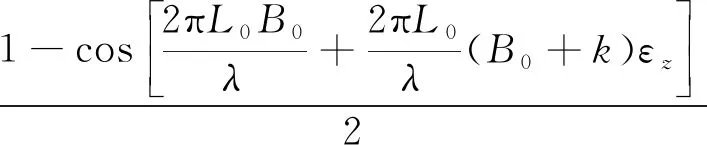
(4)
(4)式是通过双折射光纤所受应变εz描述干涉光谱T′(λ),与参考文献[4]、参考文献[6]、参考文献[20]一致,用于与下面推导的计算应变的理论表达式对比,以校验本文中推导的表达式正确性。
由(1)式、(3)式可得通过L′表示的受轴向应变后的干涉光谱表达式为:

(5)
欲使(5)式对应干涉光谱T′(λ)的值最小,则:

(6)
式中,n为整数,λn为整数n对应的波谷波长,其它依此类推。
由(6)式解出:
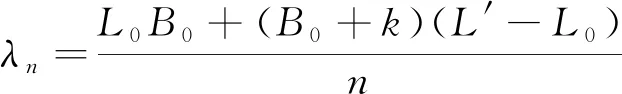
(7)
欲使(5)式对应干涉光谱T′(λ)的值最大,则:
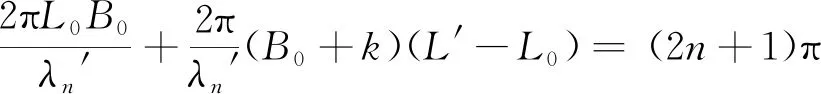
(8)
式中,λn′为整数n对应的波峰波长,其它依此类推。
由(8)式解出:
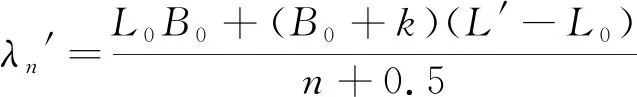
(9)
由(7)式可得:
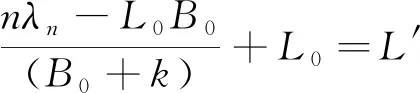
(10)
由(9) 式可得:
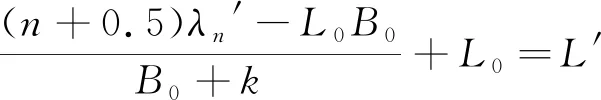
(11)
由(10)式=(11)式可得:
n=0.5λn′/(λn-λn′)
(12)
由(12)式代入(10)式可得:
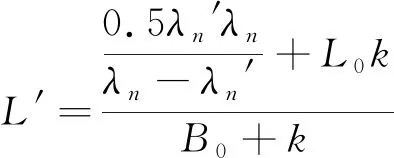
(13)
由(13)式可知,双折射光纤受轴向应变后的绝对长度L′可以由任意一组相邻的波峰波长λn′、波谷波长λn、光纤初始长度L0、光纤初始双折射率B0和双折射应变系数k求出,再将L′代入εz=ΔL/L0=(L′-L0)/L0计算双折射光纤所受应变大小。该方法可以由任意一组相邻的波峰波长、波谷波长及光纤初始条件求出双折射光纤所受应变大小。由(13)式可知,该方法与选定的监测点无关,无需进行传感器的校准;该方法无需人为判断干涉光谱左移还是右移,无需人为判断是否是周而复始的干涉光谱,有助于实现在线测量;该方法只需包含0.5个周期的干涉波形,需要的信息量更少,可以实现双折射光纤长度更短的Bi-FLM传感器的在线测量。
根据(7)式、(9)式可得:
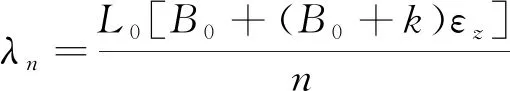
(14)
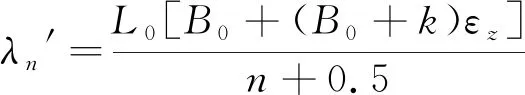
(15)
当(14)式、(15)式n值相同时,波谷与波峰相邻。由(14)式可知,当双折射光纤所受应变εz为正时,因为波长必须为正数,故n为正,此时λn>λn′;当双折射光纤所受应变εz为负应变且足够使n为负数时,此时λn′>λn。由(14)式可知,因为波长必须为正数,要使n为负数,则:
B0+(B0+k)εz<0
(16)
由(16)式可得:
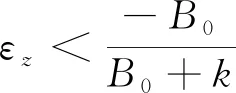
(17)
假设双折射光纤长度L0=0.1m,双折射率B0=2.6×10-4,双折射应变系数k=7.3×0.001/ε,经计算需满足εz<-0.0343915343915344ε,即εz<-34391.5343915344με时,才能使n为负数,该应变是个极大的负应变,一般情况下难于产生如此大的负应变,故一般情况下n为正。
欲使(5)式对应干涉光谱T′(λ)的值最大,则可令:
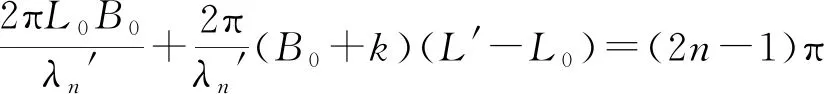
(18)
由(18)式可得:
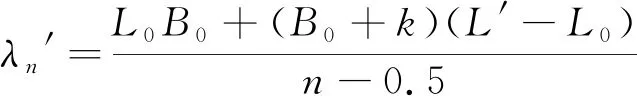
(19)
由(19)式可得:
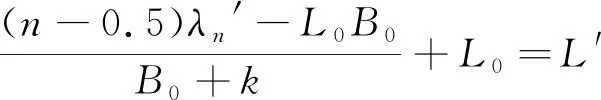
(20)
由(10)式=(20)式可得:

(21)
由(21)代入(10)式可得:
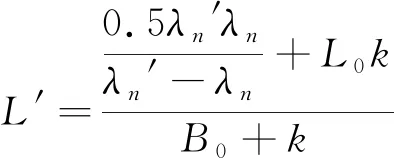
(22)
根据(19)式可得:
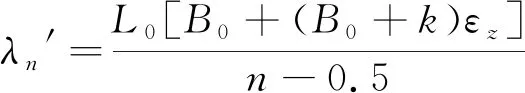
(23)
当(14)式、(23)式中的n值相同时,波谷与波峰相邻。当εz>0时,n为正,满足λn′>λn,应用(22)式计算双折射光纤受轴向应变后的绝对长度L′,并以此计算双折射光纤所受应变大小;εz≪0且足够使n为负数时,满足λn>λn′,应用(22)式计算L′,并以此计算应变大小。
比较(13)式、(22)式可知:一般情况下n为正,满足λn′<λn时使用(13)式;满足λn′>λn时使用(22)式。若已知任意一组相邻的波峰波长、波谷波长,无需判断波峰波长λn′、波谷波长λn谁大谁小,(13)式、(22)式统一为(24)式:
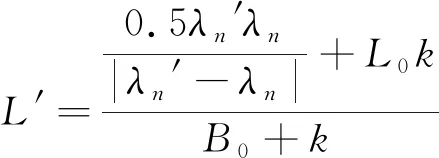
(24)
但当应变εz≪0且足够使n为负数时,应区分波峰波长、波谷波长的大小,选择合适的公式计算双折射光纤受轴向应变的大小。εz≪0且足够使n为负数时,满足λn′>λn,应用(13)式;εz≪0且足够使n为负数时,满足λn>λn′,应用(22)式。由前述可知,一般情况下难于产生足够的大负应变使n为负数,故一般情况下n为正。下面就n为正时展开讨论。
2 分析与讨论

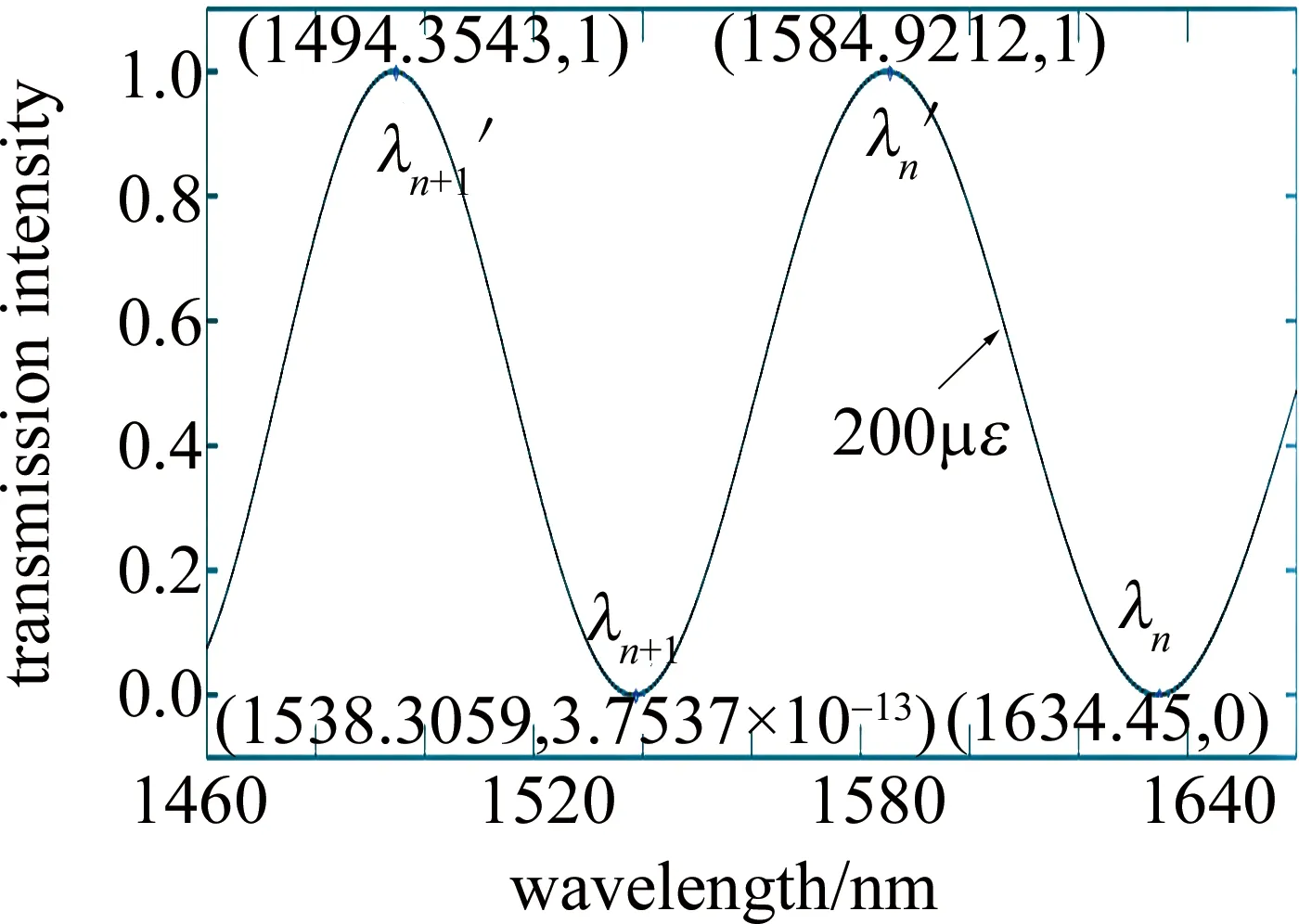
Fig.2 The Bi-FLM interference spectra by a set of adjacent wave-valley and wave-peak wavelengths near 1550nm
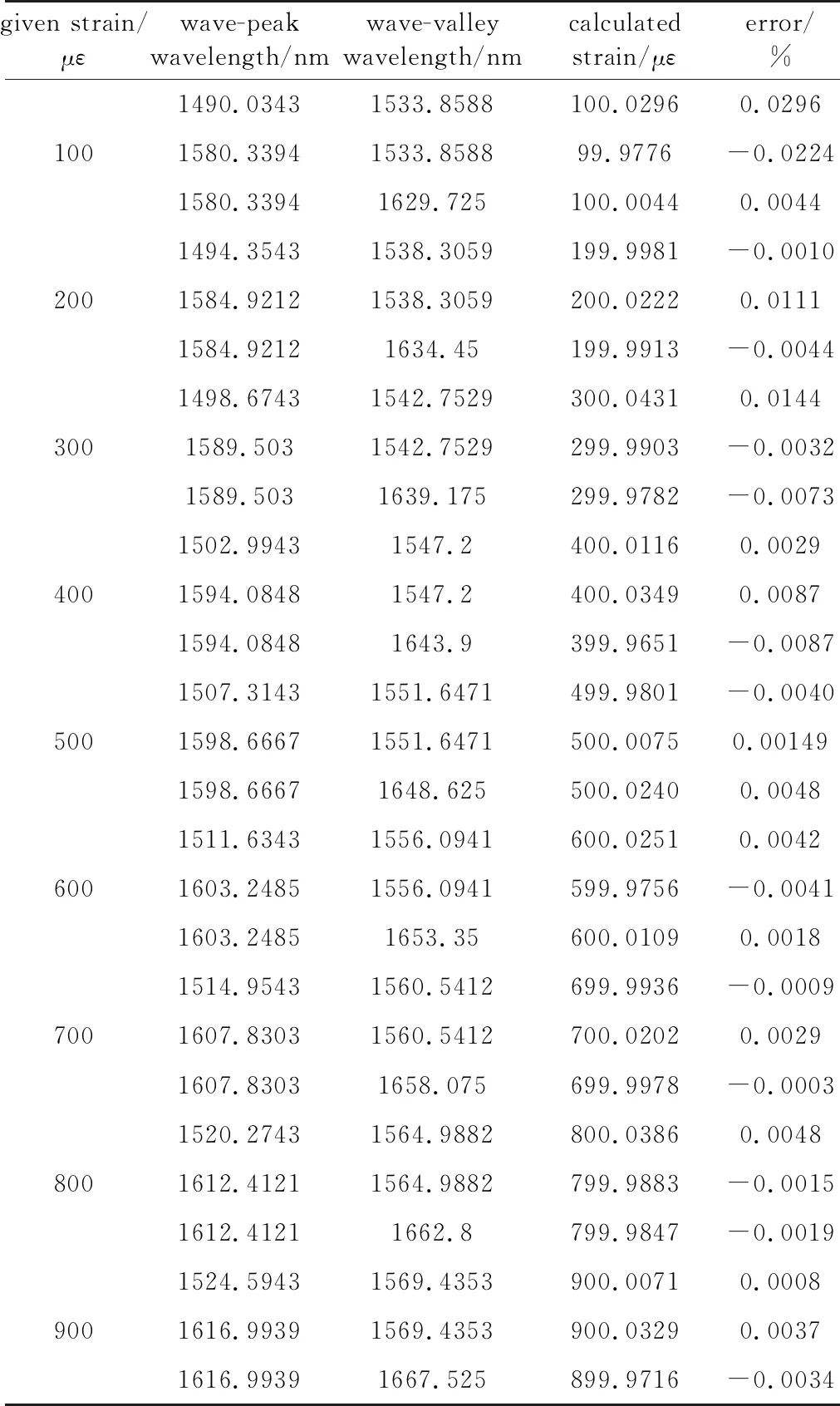
Table 1 Calculating strain results by a set of adjacent wave-valley and wave-peak wavelengths near 1550nm
从表1可以看出,统一应用(24)式便可计算双折射光纤受轴向应变大小,计算应变与给定应变基本一致。存在一定误差是由于(4)式绘制的Bi-FLM干涉光谱波形横坐标λ步长增量设置为0.0001nm,而非连续步长,导致某些波峰的纵坐标不完全等于1,或某些波谷的纵坐标不完全等于0,只是近似意义上的波峰波谷,如图2中波谷点(1538.3059,3.7537×10-13)纵坐标不完全等于0。因此,计算的应变也是近似接近理论值,从而与给定应变存在一定误差。
3 结 论
从理论上推导出由1组相邻的波峰波长、波谷波长及其双折射光纤初始长度、初始双折射率和初始双折射应变系数计算双折射光纤所受应变后的绝对长度,从而计算应变的方法,并进一步通过数值计算验证理论的正确性。
只要图形包含1组相邻的波峰波长λn′、波谷波长λn,一般情况下,无需区分波峰波长、波谷波长的大小,便可计算双折射光纤受轴向应变后的绝对长度,从而计算应变。但当应变εz≪0且足够大时,应区分波峰波长、波谷波长的大小,选择合适的公式计算双折射光纤受轴向应变的大小。由1组相邻的波峰波长、波谷波长及其双折射光纤初始条件计算应变的方法与选定的监测点无关,无需进行传感器的校准;无需人为判断干涉光谱左移还是右移,无需人为判断是否是周而复始的干涉光谱,有助于实现在线测量;只需包含0.5个周期的干涉波形,需要的信息量更少,可以实现双折射光纤长度更短的Bi-FLM传感器的在线测量。

