小纵横比光电器件发射端耦合工艺研究及优化

江秋月，仲顺顺，周雄锋*，吴国栋，马 著，孙 翔

(1.中南大学 机电工程学院，长沙 410083；2.中南大学 高性能复杂制造国家重点实验室，长沙 410083)

引 言

本文中基于2.5G BOSA，采用小纵横比(竖直和水平方向发散角比值小于2)半导体激光器，建立LD-lens-SMF的耦合模型，利用物理光线追踪法，分析耦合过程中各个方向自由度改变对模型耦合效率的影响，并搭建耦合平台进行实验验证；将仿真和实验结果进行了对比分析，得出了耦合效率对各自由度变化的敏感程度，研究结果指导了运动平台的选型和耦合设备的设计，优化了耦合封装工艺流程。

1 实体模型与耦合原理

BOSA光电元件主要由发射端(LD TO-can)、接收端(PD TO-can)、基体、SMF等零件利用胶粘和焊接等方式组合而成，如图1所示。其发射端的主要作用是将电信号转化为光信号，主要用于发射机；接收端主要作用是将光信号转化为电信号，主要用于接收机；光纤的作用是用于光信号传输[10]。图中，PD(photo-diode)是光电二极管,TO-can表示晶体管外形是罐型(transistor outline can)封装方式。

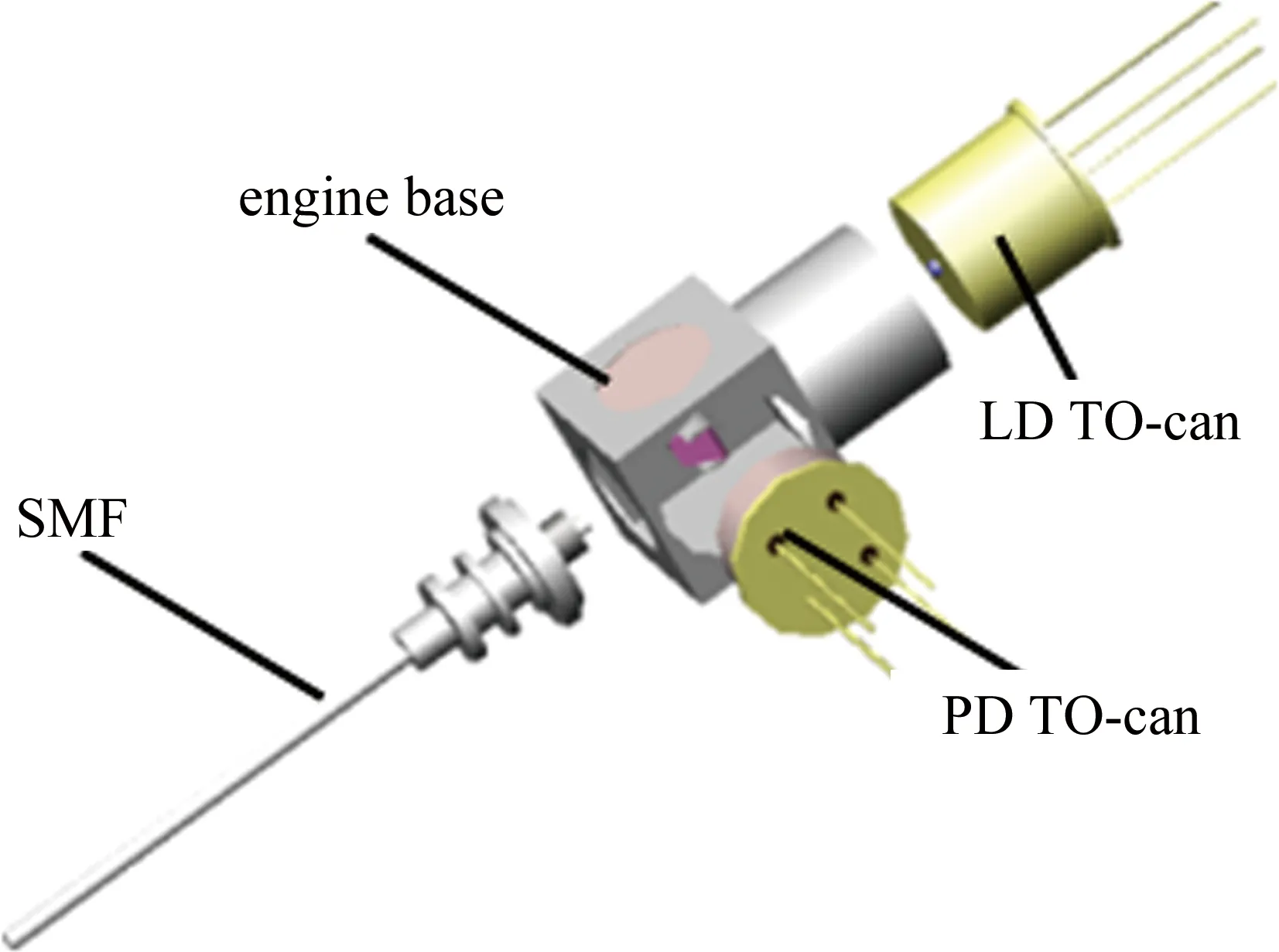
Fig.1 Bi-directional optical sub-assembly

同轴型光电子器件发射端中，LD发出的光束经过透镜的汇聚后耦合进SMF，其耦合的基本原理如图2所示。LD为单模激光器，球透镜汇聚光线，LD发射的激光经过球透镜的聚焦，在另一方向的焦点处产生光斑，移动SMF与光斑的相对位置可以改变进入光纤中光的能量高低，当SMF与LD产生的光斑两者模场达到最佳匹配时，即达到了整个系统的最佳耦合效率。

Fig.2 Coupling schematic

2 仿真模型与实验

2.1 仿真模型的建立

2.1.1 光纤及激光器参量 建立BOSA发射端的耦合模型，即实现SMF与LD的高精度耦合，首先需对光束的模场、束腰半径及数值孔径进行计算和研究。SMF芯径很小，只有8μm～10μm左右，只能传输一种模式的光，其模间色散小，适用于远程通讯，SMF模场高斯分布是旋转对称的，其数学表达式如下式所示[14]:

(1)

式中，A代表振幅，r代表光纤的径向长度，w0代表单模光纤的模场半径。

采用国产G652.B单模光纤(中心波长为1310nm,模场直径为9μm～10μm)为研究对象，其束腰半径定义为4.6μm，数值孔径为0.14。模场仿真分布如图3所示，基本为标准的圆形。

可以看出,陈、张两位先生对借代辞格的类型划分大体上是一致的。只是借代的小类名称和数量略有不同:《发凡》中的“事物和事物的作家相代”,《修辞学》中没有涉及；《修辞学》中的“以特征的喻体代本体(可以看成比喻兼借代)”在《发凡》中没有提及。

Fig.3 Simulation diagram of fiber mode field distribution

BOSA发射端内部结构如图4所示。通过设置光源类型可以模拟单模激光器光束，其光束分布可以近似看作高斯分布[15]，LD发出的光束经透镜汇聚后与SMF进行耦合，耦合前经透镜整形后在光纤端面形成的光斑如图5所示。选用的激光器类型为(InGa)(AsP)/InP双异质结小纵横比激光器，其具体参量如下：标准功率P0=6mW，加载电流30mA，工作中心波长λ=1310nm，发散角θ∥=25°,θ⊥=38.27°。激光器的数值孔径由以下两式求出[16],分别为：dNA,∥=0.363，dNA,⊥=0.537。

dNA,∥=sin(0.85×θ∥)

(2)

dNA,⊥=sin(0.85×θ⊥)

(3)

高斯函数中，发散角与光束强度为1/e2时的半角的比值为0.84932，通常取0.85[14]。dNA,∥表示水平方向的数值孔径，dNA,⊥表示垂直方向的数值孔径。得出激光器光束的束腰半径[17]：w∥=1.911μm，w⊥=3.6755μm。

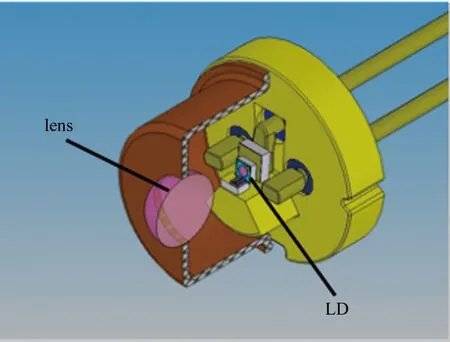
Fig.4 3-D picture of BOSA device emitter

Fig.5 Simulation diagram of mode field distribution

建立仿真模型后，设置仿真工艺参量，如表1所示。

Table 1 The value of specific parameters

2.1.2 仿真及耦合效率的计算 在光学仿真软件中，首先设置LD、透镜以及SMF的参量，通过物理光线轨迹追踪的方法，调整SMF与LD的相对位置和角度位置，使LD与SMF的模场的达到最佳匹配，从而获得最佳耦合效率。仿真耦合效率利用下式进行计算：

T=

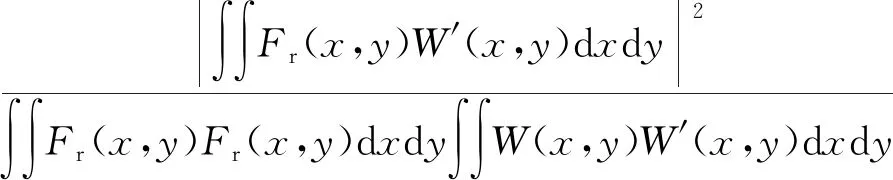
(4)

式中,Fr(x,y)是描述接收光纤复振幅的函数，W(x,y)是描述耦合到光纤中的光束的复振幅的函数，上标′表示复共轭。当光束模式的幅度和相位在所有点处完全匹配光纤模式时，实现最大接收器效率T=1.0； 模式形状或相位的任何偏差都会对T的值产生较大影响，使其减小到小于1.0。

在SMF与LD的耦合过程中，忽略光的吸收以及散射等其它情况，经过透镜汇聚的光斑模场与SMF的模场匹配程度越高，则耦合效率越大[18]，选用小纵横比的半导体激光器其模场分布更加接近于圆形，在经过球透镜聚焦后，其光斑模场与光纤模场的匹配程度更高，有利于总的耦合效率的提高。

2.2 实验平台

BOSA激光器端与光纤的耦合精度达到0.1μm量级， 因此在实验平台搭建过程中，需要选取高精密的运动平台来实现LD和SMF的相对运动，并结合全局最优搜索算法，才能达到最大的耦合效率。目前国内生产厂家合格器件通常选择在最大耦合效率处波动3%～5%为可接受范围，结合仿真结果，x,y运动方向选用日本骏河生产的型号为KYG06020-C的运动平台，该平台的重复定位精度为0.1μm，z运动方向选用型号为KYL06050-N1-C运动平台，重复定位精度为0.5μm；x′,y′运动方向(表示绕x,y旋转)的平台选用型号为KAWO6100-LA，旋转中心为100mm；可以满足本次激光器与光纤耦合试验的要求。运用实验室自行研发的LD自动耦合系统可实现LD和SMF的自动耦合对准，其基本原理为：上夹具夹持SMF保持竖直，LD插入其管座并且放入下夹具中夹紧，z轴运动平台保

Fig.6 Diagram of the coupling platform

证光纤与LD的纵向距离，x,y运动平台保证SMF与LD的横向距离，x′,y′运动平台保证LD分别绕x,y轴旋转，将激光二极管插座和光纤尾端分别通过导线和探头连入光功率计即可对耦合功率的变化情况进行实时监测。耦合平台实物图如图6所示。

3 结果与讨论

3.1 最大耦合效率比较分析

仿真得到的最大耦合效率为64.29%，并不能达到理想的100%耦合效率。分析原因如下：虽然本文中采用的激光器快轴和慢轴发散角十分接近，但是球透镜不能对光束进行整形，这就导致在光纤端面仍然形成了一个椭圆形，光斑模场与光纤模场并不匹配；同时由于球透镜存在球差(见图7)，导致光线难以聚焦到一点，如图8所示。在入瞳半径为0.6684mm时，球差的尺寸为1.584mm，这导致产生的光斑的尺寸要大于单模光纤模场的尺寸；另外，透镜对光线具有吸收作用以及激光在传输过程中存在折射、衍射等情况，均会造成传输过程中能量的损耗。以上几点造成了模型的耦合效率为64.29%。

Fig.7 Coupled simulation diagram

Fig.8 Spherical aberration distribution

在实验过程中，为避免实验出现偶然误差，选取3组相同规格的LD TO-can和SMF，分别放在搭建的耦合平台上进行光功率搜索，通过光功率计实时监控耦合功率，并读取其最大功率记录。经过后期数据处理，得到实际的最大耦合效率为51.46%。

对比仿真和实验结果可以看出，理论的耦合效率与实际耦合效率存在约13%的误差，主要原因有以下几点：(1)透镜的实际生产中不可能为理想球形，产生的球差相比较仿真系统中要大，这会导致光线汇聚更为分散，造成耦合效率减小；(2)系统仿真时，透镜表面涂有一层抗反射膜，可以有效减少菲涅耳反射，提高耦合效率，实际试验中球透镜的镀膜工艺存在限制，并不可能在表面镀一层均匀完整的抗反射膜，因此会造成光线反射，减少通光量；(3)LD芯片发光功率不恒定，对耦合效率也存在影响。另外，在实际生产加工过程中，器件的贴片工艺、实验平台的精度以及算法的优良程度都对最大耦合效率产生一定的影响，综合分析，实际与理论存在约13%的耦合误差属于可接受范围。

3.2 容忍度比较分析

3.2.1 水平范围容忍度分析比较 耦合效率随x,y轴偏移量的变化如图9所示。当角度偏差忽略不计且纵向距离位于最佳位置时，仿真与实验耦合效率均随x,y偏移量的增加而下降，且仿真耦合效率均高于实验值。以耦合效率下降一定值时x,y方向偏移量的大小定义为x,y方向的容忍度，现以仿真结果为例进行定义说明(实验结果的定义与仿真类似)，即当耦合效率下降As时，若x,y方向偏移量分别为xs和ys，则x,y方向容忍度分别为xs和ys，如图9所示。当仿真耦合效率As和实验耦合效率Ae均为10%，即耦合效率下降10%时，仿真值xs和实验值xe均为1.1μm左右，仿真值ys和实验值ye均为1.5μm左右。x,y方向的容忍度有一定的差距，主要是因为LD的光束发散具有快轴和慢轴的区别，快轴的发散角要大于慢轴的发散角，因此在远场形成的光斑只是类似于高斯光束的椭圆光斑，由此导致LD在与SMF的模场耦合中x,y方向的容忍度略有区别。通过图9还可以看出：耦合效率对x,y方向的位移变化相当敏感，容许度非常小；当LD与SMF的相对位置达到了5μm时，耦合效率下降50%左右， 因此在做x,y方向的运动平台选型时，首先要确保平台的运动精度要在亚微米级别，

Fig.9 Planar offset vs. coupling efficiency

否则运动平台的微小移动都会造成耦合效率的急剧降低，无法达到耦合要求。

3.2.2 纵向范围容忍度分析比较 耦合效率随z轴偏移量的变化如图10所示。由图可知，在保证角度偏差忽略不计且横向(x,y轴)位置位于最佳时，仿真和实验耦合效率随z轴位移的变化趋势基本相同。对比x,y轴容忍度可以发现：纵向(z轴)耦合效率对位移的敏感度远不如横向位移。当SMF与LD的距离增加或减少50μm(仿真值zs和实验值ze分别为50μm)，仿真耦合效率下降7%左右,即As≈7%，实验耦合效率下降10%左右，即Ae≈10%，实际与理论存在3%左右的偏差，主要因为在耦合平台装配过程中，z轴与x,y方向并不能保证绝对的垂直，而是存在一定的角度偏转，同时零件加工误差也会对实验耦合效率产生一定影响，导致理论与实际出现偏差,这种偏差在允许范围内。通过纵向距离对耦合效率影响的分析发现，z轴运动平台的精度达到微米级别就能完全满足耦合要求。

Fig.10 Longitudinal offset vs. coupling efficiency

3.2.3 角度旋转范围容忍度分析比较 目前所研究的2.5G BOSA，其SMF的结构是旋转对称的，且LD中未封装隔离器，所以z方向角度的旋转变化对耦合效率的影响很小，在此不作分析。为方便研究，现假设x,y,z方向处于最佳耦合位置，仅分析x,y方向偏转对耦合效率的影响[19-22]。由图11可知，仿真和实际验

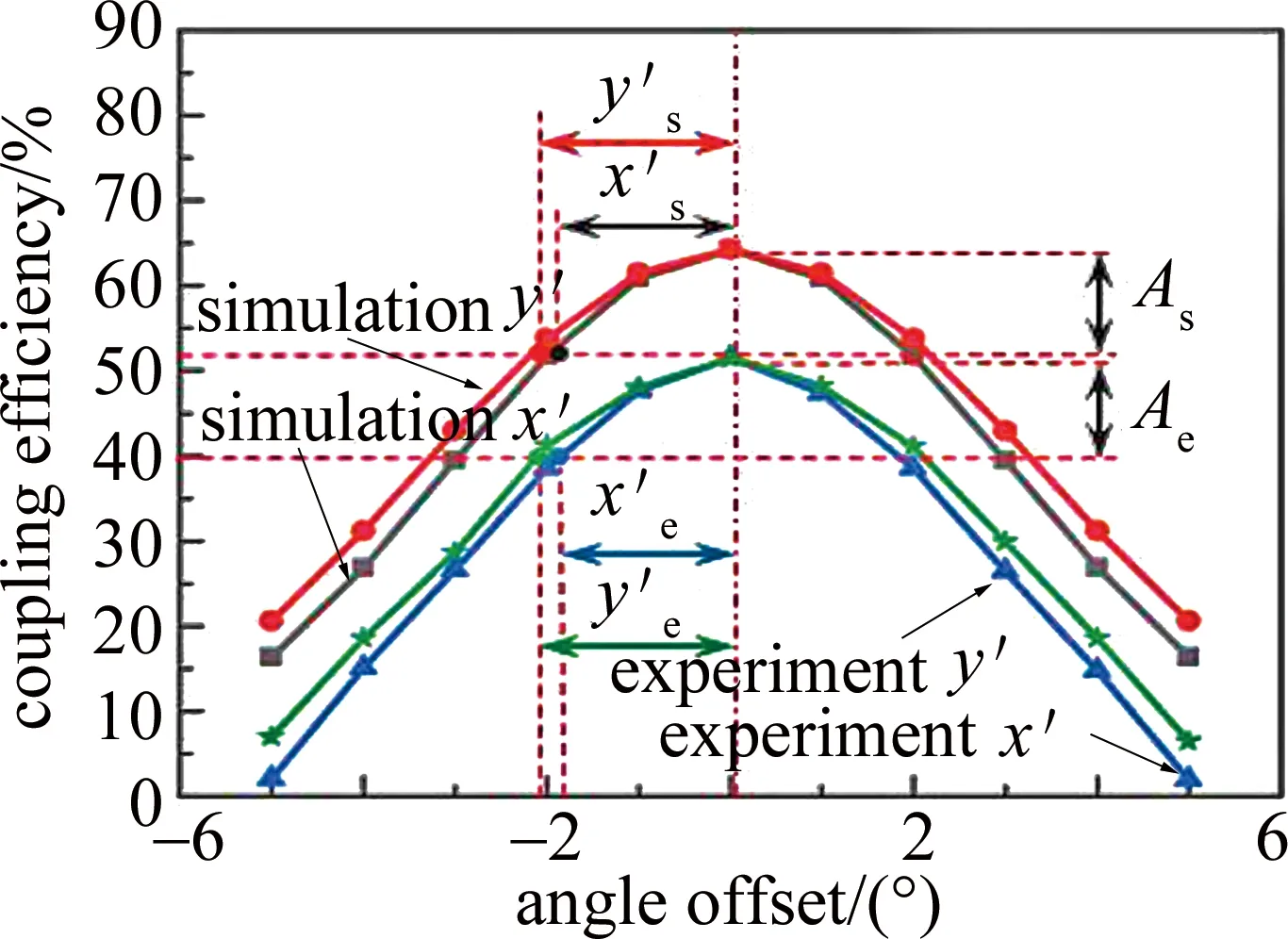
Fig.11 Angle offset vs. coupling efficiency

3.3 大纵横比激光器对比实验

选用较大纵横比(竖直和水平方向发散角比值大于2)的半导体激光器进行对比实验，其发散角为θ∥=15°,θ⊥=41.25°，得出激光器光束的束腰半径为：w∥=3.1855μm，w⊥=9.108μm。仿真得到的最大耦合效率为34.44%，选取3组相同规格的LD TO-can和SMF进行耦合实验，经过后期数据处理，得到实际的最大耦合效率为21.34%。分析原因可知：因为采用的激光器快轴和慢轴发散角差距较大，球透镜的折射率是有限的，得到的光斑尺寸大于小纵横比器件的光斑，光斑模场与光纤模场不匹配程度更高，从而导致耦合效率较低。在其它条件满足最佳时，对x轴、y轴、z轴以及x′,y′角度进行一定量的偏移，得出其偏移量与耦合效率之间的关系如图12所示。

通过对容忍度的分析发现，大纵横比半导体激光器耦合时的容忍度要略高于小纵横比半导体激光器，这是因为大纵横比半导体激光器光束经过耦合之后在光纤端面形成的光斑尺寸更大，而光纤模场半径尺寸是固定的，这就造成两者之间耦合会有更大的容忍度。但是，大纵横比半导体激光器的最大耦合效率远低于小纵横比半导体激光器的最大耦合效率；在光通信系统中，更大的耦合效率意味着更长的信号传输距离和更低的网络搭建成本。因此，在耦合平台的精度满足要求的情况下，选择小纵横比半导体激光器进行器件的制造，更加具有优势。

Fig.12 Planar offset vs. coupling efficiency

3.4 耦合流程优化

BOSA包括发射端和探测端，每一步流程都会对器件最终性能产生影响，本文中仅讨论发射端耦合工艺流程。通过上述仿真与实验研究可以发现，小纵横比半导体激光器的耦合效率敏感度因子由大到小分别是：x轴、y轴位移的耦合效率敏感度因子>x′轴、y′轴角位移的耦合效率敏感度因子>z轴位移的耦合效率敏感度因子。因此，进行自动化耦合时，在保证一定的纵向高度和较小偏转角度前提下，首先要进行平面范围内的光功率搜索；在找到平面位置的最佳耦合点后，进行x′,y′的角度旋转搜索，同时还要结合平面搜索，因为装配误差的存在，角位台在旋转时不可能保证LD刚好位于旋转中心，旋转时总会存在一定的横向位移，进行平面搜索的目的是保证再次找回最佳平面耦合点；最后进行纵向范围内的光功率搜索，因为装配误差的存在，此时同样需要配合平面搜索才能找到整个系统的最佳耦合位置。

4 结 论

建立了同轴型半导体激光器与单模光纤的耦合模型，通过仿真比较分析了模型的耦合效率与各个方向位移敏感度的关系，并搭建自动耦合平台研究了实际耦合过程中耦合效率与各个方向容忍度的关系，与仿真的结果进行比较，发现仿真与实验的结果基本吻合；最后，对同轴型半导体激光器与单模光纤的耦合流程进行了优化。

(1)小纵横比LD与SMF进行耦合，实际效率可达51.46%；水平面范围内的位置变化对耦合效率的影响最为显著，其次是LD与SMF的角度偏差，最后是LD与SMF之间的纵向距离。因此，LD-TO-can的封装要尽量控制LD中心与透镜中心在水平面的偏差，确保两者中心位于同一轴线，以保证耦合效率。

(2)耦合封装时在x,y方向选择分辨率为0.1μm的运动平台，x′,y′方向选择分辨率为0.1°的运动平台，z方向选择分辨率为1μm的运动平台可以基本保证LD和SMF的耦合精度，达到生产要求。

(3)耦合效率曲线存在明显的峰值且变化敏感，容许度很小，这对耦合设备的稳定性提出了更高的要求，同时对后续的焊接封装带来极大挑战。

(4)对比x,y发散角差异较大的大纵横比半导体激光器，在耦合平台精度满足要求的情况下，采用小纵横比的LD可以提高光电器件发射端的耦合效率，采用折射率渐变的透镜可以有效减少球差造成的影响，提高耦合效率。